电磁脉冲驱动套筒内爆压缩磁化靶研究*

刘 斌，李 成，王瑞星，曹启伟，杨显俊,3

(1.中国工程物理研究院研究生院,北京 100088；2.中国工程物理研究院聚变能源科学技术研究中心,北京 100088;3.北京应用物理与计算数学研究所,北京 100094)

磁约束聚变或者惯性约束聚变是目前实现聚变的主要传统研究途径，但这两种传统聚变途径面临的最主要挑战是达到点火条件所需要的约束时间和点火密度取值皆处于两个极端情形。由此，这两种传统的聚变途径带来了设施庞大花费不菲以及耗时耗力的后果。为了改变这一状况，近年来，国际聚变学术界提出惯性磁约束聚变(magneto inertial fusion, MIF)的新途径，主要利用电磁内爆的方式，通过固体套筒绝热压缩具有较高初始温度的预加的磁化等离子靶，使等离子温度不断升高最终达到聚变点火条件。这一新的聚变途径由于可能会以最小代价在最短时间内实现聚变装置的小型紧凑而受到广泛关注。MIF具有多种候选方案，其中包括场反位型压缩方案[1-3]、磁化套筒惯性聚变方案[4-5]、磁化激光惯性约束靶聚变方案[6-7]、液体金属内爆压缩磁化靶方案[8]、等离子套筒压缩方案(PLX)[9-10]。其中最具代表性的磁化套筒惯性聚变方案最近的实验结果显示获得了超过1012个聚变高能中子产额[13-14]，由此完全证实了磁-惯性约束聚变途径的科学可行性问题。近年来，中国在这一领域也开展了初步的研究工作。中国工程物理研究院基于磁-惯性约束聚变途径已初步取得预期的与理论分析及数值模拟一致的实验结果[11-12]。同时，还拥有先进的脉冲装置聚龙一号(PTS)[15]，为开展类似MagLIF的研究工作打下了很好的基础。本文中拟对电磁脉冲驱动下套筒内爆压缩磁化靶过程进行研究，希望通过一维MHD方程和有限差分法[16]，研究内爆过程、电子离子热传导效应、α粒子能量沉积及内爆压缩做功等问题，以期为后续工作的开展提供一定的基础。

1 物理模型和分析方法

1.1 物理模型

对于电磁脉冲驱动套筒内爆压缩磁化靶的过程，本质上是Z箍缩过程，且内爆压缩内嵌有轴向磁场的燃料产生的超强磁场[17]会对带电粒子产生重要的影响，但这与通常丝阵负载的Z箍缩和动态黑腔内爆过程[18]是不同的，主要是依靠套筒的惯性进行直接驱动。这里研究较为简化的模型，即考虑固体套筒内部为均匀Z方向常磁场，燃料的初始密度和初始温度分布均匀，且通过外部加压(爆轰或强电流)对套筒及磁化靶进行压缩。

拼装示意图如图1所示，采用燃料及套筒(填塞层)初始等压拼装。p0为初始热压强，T0为燃料层初始温度。内层为等摩尔DT燃料层，燃料层热压强、密度和半径分别用pf、ρf和Rf表示。外层为套筒层，套筒层热压强、密度、半径和温度分别用pt、ρt、Rt和Tt表示。套筒材料一般选用为铍、铝、铜等金属材料。金属套筒在Z向加载电流以Z箍缩的方式内爆压缩磁化靶。

对于上述拼装方法，燃料层压强和套筒层压强满足：

(1)

实际上描述套筒状态连续变化过程非常困难，所以采用上面关系式中显示的近似描述方式，将套筒层的状态划分为常温区和热区2个部分[19]。采用的DT燃料是低Z物质，一般是光性薄的，忽略辐射项，则燃料层压强为电子压强和离子压强之和。对应的套筒层声速ct和密度及压强存在如下关系:

(2)

1.2 分析方法

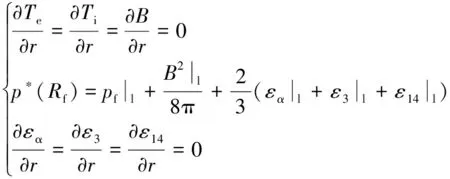
(3)

式中：Te、Ti分别为电子、离子温度，B、B|l、B|r分别为为磁感应强度及左、右边界磁感应强度，εα、ε3、ε14和εα|l、ε3|l、ε14|l分别为3种聚变产物(3.5 MeV α粒子、3 MeV质子、14.7 MeV质子)的体积能量密度及左边界处3种聚变产物的体积能量密度，pt|r为右边界的热压，pp为电磁脉冲驱动压。

套筒层的某一节点在时间点tk热压强与其密度、速度、坐标、时间的关系满足：

(4)

对于套筒，外边界压强为脉冲电流产生的磁压，套筒层内部压强应取扩散进套筒内部的磁场产生的磁压，所以压强分布为:

(5)

式中：c为光速，Im为电磁脉冲函数。磁压pB中的磁场由拉氏坐标下的磁扩散方程决定：

(6)

式中：V≡1/ρ，m、η⊥分别为套筒的质量和电导率。

对于式(4)采用中心差分，得到差分方程:

(7)

差分方程的系数矩阵为带状矩阵，且对角线按列严格占优，所以采用Gauss-Seidel迭代法[20]求解收敛。这样就把电磁脉冲驱动转化为数值计算时差分方程的具体形式。文献[23]中采用零维模型分析的压缩比、内爆速度等结果以及文献[5]中数值模拟得到的能量输出等结果与本文中建立的简单模型和数值结果进行比对，结果基本吻合。因此可以认为本文中模型和数值算法的计算结果是基本可信的。

2 理论分析和数值模拟结果

2.1 内爆过程及套筒材料对内爆影响

考虑套筒材料为金属材料，忽略欧姆电导率细微的差别。套筒的状态按照式(1)和(2)描述。套筒内外半径分别为2.90、3.48 mm，预加热温度为250 eV，初始内嵌磁感应强度为30 T，脉冲形式取正弦函数，峰值电流为27 MA，脉冲电流周期为600 ns，加载在套筒上的时间为150 ns，燃料密度为3×10-3g/cm3。当套筒材料分别铝和铜时，模拟结果显示各个格点随压缩过程的变化如图3所示。

从图3中可以看出，套筒材料对内爆压缩时间有影响。考虑简单结构(准均匀的DT套筒):

(8)

式中：Et为单位长度总能量，Ml为单位长度套筒质量，g/cm；vi为内爆速度，Rt和pt分别为套筒的半径和压强。由式(8)可以得出惯性约束时间tc满足:

(9)

式中：内爆时间ti≈R0/vi，R0为初始半径，Cr=R0/Rt为半径压缩比。

相同驱动条件下，不同套筒材料惯性不同，惯性大的套筒内爆速度小，而惯性小的套筒内爆速度大，对应的约束时间也不同。不考虑套筒层，只考虑等离子燃料层情况下，聚变反应时间和约束时间为[20]：

(10)

式中：〈σv〉DT为DT平均反应率，Rf为燃料的半径，cs为声速。

由式(10)中左右两式相除得:

(11)

对于等摩尔的DT等离子体，离子平均质量mf=2.5mp,mp为质子质量，所以n=ρf/mf，将其代入式(11)可得:

(12)

实际上,式(12)为nτ型劳逊判据与ρR型劳逊判据的转化关系[ 20]。考虑套筒时，式(12)中的tc必须用式(10)进行修正，所以套筒材料对惯性约束时间以及点火条件都有重要影响。将燃料层从内到外划分为80个网格点，套筒层划分为60个网格点。燃料层第40格点处电子与离子升温如图4所示。

内爆压缩过程中，电子离子温度可上升到约50 keV，电子离子温度历史基本吻合，由Braginskii方程可以得出：

(13)

式中：τe为电子碰撞弛豫时间，W为外界对等离子体做功功率，A和Λ为碰撞参量，因此粒子数密度较大，碰撞较为频繁，对应的弛豫时间很小，电子离子历史基本保持一致，但是如果如图3中半径曲线反弹，粒子数密度下降到一定程度，则电子离子温度历史会有一定的分离。等离子燃料密度和压强的变化，如图5所示，等离子密度和和压强满足关系：p∝ρT，分别考察燃料层的第1、20、40、60个网格格点燃料密度和压强的变化，如图5所示。

从图5中可以看出从外层格点到内层格点，燃料密度和压强都是外层先增大，内层后增大，这与图3(a)中显示的外部格点先被压缩，内部格点后被压缩的趋势相吻合。

2.2 内爆过程中电子离子热传导效应

初始内嵌磁感应强度为分别为0、1、5、10、20和30 T时5种情况。网格格点划分不变。电子热传导的能量损失为：

ΔE=2πRfkc(kT)≈2πkckT

(14)

式中：T为温度，k为玻尔兹曼常数，kc为传导系数，假定kT≈kT/Rf。当电子传导率被强磁场限制时，必须考虑离子传导率[4]。电子和离子热传导系数κe和κi通过Braginskii方程[22]给出(ne=ni=n)。热传导损失率为:

(15)

当内嵌磁感应强度分别为0、1、5、10、20、30 T时，考察第40个格点处的电子热传导系数，模拟结果如图6所示。磁感应强度的增加有效的减小了电子热传导系数，抑制了电子热传导。当磁场大于5 T时电子热传导系数比无磁场时减小了两个数量级，当磁感应强度为30 T时电子热传导系数比无磁场时减小了3个数量级。这说明磁场对于抑制电子热传导是非常重要的。

考察内嵌磁感应强度分别为0、1、5、10、20、30 T时，离子热传导系数变化情况，如图7所示。对比图7和图6，离子热传导系数比电子热传导系数小超过1个数量级，由于电子低质量、高速率的性质，电子热传导显然要比离子热传导强。由于离子的高质量，约束离子所需的磁场也就要比电子强，当磁感应强度为30 T时，离子热传导系数下降明显，相比于其他情况，离子热传导系数下降了为原来的1/10。

2.3 内爆过程中α粒子的能量沉积

分析磁场增加α粒子的能量沉积的情况。fα为α粒子能量沉积的比例。使α粒子停下来的，贡献最大的是和等离子体电子的小角度碰撞，显然0

(16)

(17)

式中：q为α粒子的电荷，c为光速。求解该方程，即可得到α粒子各方向上的速度分量，然后就可以求得α粒子的运动距离，最后在整个柱坐标空间积分便可求得α粒子的沉积比例，整个求解过程可以参考文献[22]。这里通过MHD模拟给出磁场对α粒子能量沉积的影响，模拟结果如图8所示。

如图8所示，当内嵌磁感应强度分别为0、1、5、10、20、30 T时，α粒子能量沉积密度Eα相对增加。可以看出，在压缩峰值处，磁感应强度为5、10、20、30 T时α粒子能量沉积密度比磁感应强度为0和1 T时相对增加了大约200倍以上。同时，在压缩峰值处，磁感应强度为5、10、20、30 T时α粒子能量沉积密度相差不多，这是因为较大磁场产生的磁压会导致等离子体的压缩变得困难，使得压缩率和温度在某种程度上降低，这又会抵消磁场对α粒子能量沉积增加的作用。所以磁化靶的磁场并不是越强越好，而是要综合它对电子离子热传导抑制、α粒子能量沉积、压缩做功的影响，选出最优解。

这里定义ET=E-WB，E为反应释放的总能量，磁场对压缩过程的影响用磁场阻滞功WB表示，则ET可表示用于等离子体加热的能量。以ET作为磁感应强度选取的标准。当参数选取和前文中相同时，磁感应强度选取从0～50 T，则ET数据的拟合结果如图9所示。

由图9知，当磁感应强度在20～35 T之间时，ET的值相对较大。对于前文中的初始参数，磁感应强度在20～35 T为最优范围。对于其他初始参数的选择，也可以通过定标量ET来选取合适的磁感应强度的取值范围。

2.4 内爆压缩的做功过程

内爆压缩过程中，脉冲电流产生的强压压缩磁化等离子体，等离子体的热压p和动态内嵌磁场产生的磁压pB对压缩过程起粘滞阻碍作用。考虑1个等离子微元，如图10所示，主要作用项包括电磁脉冲压，热压，磁压3个部分。考虑简单结构(准均匀的DT套筒)的总能量(每单位长度)可以写成:

(18)

式中：Wdr和Rf分别为驱动功率和燃料的半径。内爆时间ti和惯性约束时间的关系如式(10)所示。

驱动功率满足:

(19)

收支平衡条件为:

(20)

式中：EDT为DT反应释放能量(17.6 MeV)，n为粒子数密度(在峰值压缩处)，〈σv〉DT只是温度T的函数。将式(20)代入式(19)中，可得:

(21)

进一步整理得:

(22)

实际上，当燃料不考虑磁化时就不存在右边第二项，驱动功率满足关系：

(23)

对于固定点火温度T(典型温度接近10 keV)，驱动功率与ρfRf平方成正比[22]。考虑磁化时，由式(22)可知，对于驱动功率一定、点火温度固定的情况下，pB越大，相应所达到的ρfRf值越小，点火也就越困难。磁化带来的做功的弊端可以通过提升驱动电磁脉冲的功率来克服，而压缩结束，发生点火时，磁化对减少电子离子热传导能量损失及增加α粒子能量沉积的好处则起主导作用。

3 结 论

通过对电磁脉冲驱动套筒内爆压缩磁化靶过程构建物理模型，利用磁流体力学和数值分析方法对内爆过程、磁场对带电粒子作用机制、磁化对压缩做功的影响进行分析。结果表明：电磁脉冲驱动套筒压缩磁化靶到达高温高压的物质状态，电子离子温度可达约50 keV，压强约1 TPa，粒子数密度达1024cm-3。套筒的材料对约束时间产生了影响，驱动功率一定时，惯性大的材料约束时间更长。内爆过程中产生的强磁场有效的降低了电子和离子热传导系数，抑制了热传导能量损失，且增加了α粒子的能量沉积，当磁感应强度超过5 T时，α粒子的能量沉积比没有内嵌磁场时增加超过了两个数量级。当驱动功率一定时，磁化降低了内爆压缩后燃料达到的ρRf值。这个弊端可以通过提升驱动功率克服，考虑磁化的主要原因是磁场对于抑制电子离子热传导和增加α粒子的能量沉积。

参考文献：

[1] TACCETTI J M, INTRATOR T P, WURDEN G A, et al. FRX-L: A field-reversed configuration plasma injector for magnetized target fusion[J]. Review of Scientific Instruments, 2003,74(10):4314-4323.

[2] DEGNAN J H, AMDAHL D J, Domonkos M, et al. Recent Magneto-inertial fusion experiments on FRCHX[C]∥24nd IAEA Fusion Energy Conference. San Diego: 2012.

[3] WUEDEN G A, GRABOWSKI T C, DEGNAN J H, et al. Increased FRC lifetimes using a longer trap[C]∥Bulletin of the American Physical Society (APS Meeting), 2013:58.

[4] SLUTZ S A, HERRMANN M C, VESEY R A, et al. Pulsed-power-driven cylindrical liner implosions of laser preheated fuel magnetized with an axial field[J]. Physics of Plasmas, 2010,17(5):263-52.

[5] CUNEO M E, HERRMANN M C, SINARS D B, et al. Magnetically driven implosions for inertial confinement fusion at sandia national laboratories[J]. IEEE Transactions on Plasma Science, 2012,40(12):3222-3245.

[6] GOTCHEV O V, KNAUER J P, CHANG P Y, et al. Seeding magnetic fields for laser-driven flux compression in high-energy-density plasmas[J]. Review of Scientific Instruments. 2009,80(4):495.

[7] HOHENBERGER M, CHANG P Y, FIKSEL G, et al. Inertial confinement fusion implosions with imposed magnetic field compression using the OMEGA Lasera[J]. Physics of Plasmas, 2012,19(5):139.

[8] LABERGE M. Experimental results for an acoustic driver for MTF[J]. Journal of Fusion Energy, 2009,28(2):179-182.

[9] HSU S C, WITHERSPOON F D, CASSIBRY J T, et al. Overview of the plasma liner experiment (PLX)[C]∥Bulletin of the American Physical Society (APS Meeting), 2009:56.

[10] GARANIN S F, MAMYSHEC V I, YAKUBOV V B. The MAGO system: Current status[J]. Plasma Science, IEEE Transactions, 2006,34(5):2273-2278.

[11] 孙奇志,方东凡,刘伟,等.“荧光-1”实验装置物理设计[J].物理学报,2013,62(7):000507.

SUN Qizhi, FANG Dongfan, LIU Wei, et al. Physical design of the “Ying-Guang 1” device[J]. Acta Physica Sinica, 2013,62(7):000507.

[12] 李璐璐,张华,杨显俊.反场构型的二维磁流体力学描述[J].物理学报,2014,63(16):165202.

LI Lulu, ZHANG Hua,YANG Xianjun.Two-dimensional magneto-hydrodynamic description of field reversed configuration[J]. Acta Physica Sinica, 2014,63(16):165202.

[13] GIBBS W W. Triple-threat method sparks hope for fusion[J]. Natrue, 2014,505(7481):9-10.

[14] GOMEZ M R, SLUTZ S A, SEFKOW A B, et al. Experimental verification of the magnetized liner inertial fusion (MagLIF) concept[C]∥IEEE International Conference on Plasma Sciences, 2014:1.

[15] 邓建军,王勐,谢卫平,等.面向Z箍缩驱动聚变能源需求的超高功率重复频率驱动器技术[J].强激光与粒子束, 2014,26(10):100201.

DENG Jianjun,WANG Meng, XIE Weiping, et al. Super-power repetitive Z-pinch driver for fusion-fission reactor[J].High Power Laser and Particle Beams, 2014,26(10):100201.

[16] BASKO M. A1-D 3-T hydrodynamic code for simulating ICF targets driven by fast ion beams[R].Version 4. Institute for Theoretical and Experimental Physics, Moscow, 2001.

[17] 邓爱东,张华,杨显俊.电磁驱动产生超强磁场的参数优化设计[J].高压物理学报,2015,29(2):123-128.

DENG Aidong, ZHANG Hua,YANG Xianjun. Parameters optimization of the strong magnetic gield generation driven by electromagnetic force[J]. Chinese Journal of High Pressure Physics, 2015,29(2):123-128.

[18] 宁成,丰志兴,薛创.Z箍缩驱动动态黑腔中的基本能量转移特征[J].物理学报,2014,63(12):125208.

NING Cheng, FENG Zhixing, XUE Chuang. Basic characteristics of kinetic energy transfer in the dynamic hohlraums of Z-pinch[J]. Acta Physica Sinica, 2014,63(12):125208.

[19] ANDREAS J K. Magnetized cylindrical implosions driven by heavy ion beams[R]. Max Planck Institute of Quantum Optics, 2001.

[20] 谷同祥,安恒斌,刘兴平,等.迭代法和预处理技术:上册[M].北京:科学出版社,2015:78-90.

[21] MEYER-TER-VEHN J.惯性聚变物理[M].沈柏飞,译.北京:科学出版社,2008:28-31.

[22] BASKO M M, KEMP A J, MEYER-TER-VEHN J. Ignition conditions for magnetized target fusion in cylindrical geometry[J]. Nuclear Fusion, 2000,40(1):41-45.

[23] 刘斌,李成,邓爱东,等.脉冲驱动磁化等离子体内爆升温点火的数值模拟[J].强激光与粒子束,2016,28(7):075010.

LIU Bin, LI Cheng, DENG Aidong, et al. The numerical modeling about ignition and implosion heating process of magnetized plasma driven by pulsed-power[J]. High Power Laser and Particle Beams, 2016,28(7):075010.