基于Cowper-Symonds方程的相似理论修正方法*
苏子星,何继业
(1.西北工业大学航空学院,陕西 西安 710072;2.西北工业大学航天学院,陕西 西安 710072)
相似理论是实验设计中较为热门的研究问题[1],其核心在于确定外载条件相似系数、以使模型与全尺寸原型实验结果接近。经典相似理论[2]成熟、有效,已在(准)静态实验中广为应用;然而近年来,具备高速、高应力、高应变率等特点的动态实验(如冲击实验等)逐渐成为研究重点。由于动态实验中的特征参数存在非线性特点,若继续使用经典相似理论作为指导,则会给实验结果带来较大误差。因此,有必要对经典相似理论进行修正。
针对冲击实验,谈庆明[3-4]曾就冲击相似律进行过详细的分析和讨论。Calladine等[5]提出通过改变外载条件来抵消应变率效应影响,并给出了修正方法。Oshiro等[6]经过严格的数学推导,进一步修正了基于经验的Calladine相似理论。
本文中在已有研究基础上,引入Cowper-Symonds方程来考虑材料本构中应变率效应影响、并重新推导外载条件相似系数的计算公式;通过数值模拟将该方法与已有相似理论进行对比,以分析该方法的模型预测精度。
1 理论基础
早期的相似理论认为:模型相当于从全尺寸原型上分离出的微元;除了尺寸与质量上的差异外,模型各物理量(如速度、应变率等)和外载条件均应与全尺寸原型相同。显然,该理论忽视了因尺寸效应而产生的相似系数变化,故模型与全尺寸原型实验结果相差较大。
自Π定理建立后,出现了MLT (mass-length-time)相似理论。该理论基于量纲一致原则提出,在确定基本物理量的相似系数后、其余物理量的相似系数均可通过Π定理求得。MLT相似理论中部分物理量的相似系数为:几何长度,λ;体积,λ3;质量,λ3;时间,λ;速度,1;压力,λ2;应力,1;应变,1;应变率,1/λ。
MLT相似理论对于(准)静态实验具有重要指导意义。但由于该理论对速度等特征参数计算的线性相似系数不够精确,故在指导动态实验时存在不足之处。
Calladine等[5]对MLT相似理论进行了修正、并提出Calladine相似理论。该理论将速度相似系数λv由1改为λ,相应的质量相似系数λm由λ3改为λ。这一做法在部分冲击问题中取得了较好的结果,但在更一般的冲击实验中其预测结果误差较大、普适性不足;故仍有改进的必要。
Oshiro等[6]从Norton-Hoff公式出发,提出了VSG (velocity-yield stress-mass)相似理论。Norton-Hoff公式[7]的表达式为 :
(1)

VSG相似理论的质量相似系数λm与MLT相似理论相同:λm=λ3;而速度相似系数λv为:
(2)
式中:λσ0是模型与全尺寸原型材料的(准)静态屈服应力比,即λσ0=σ0m/σ0p;下标m、p分别代表模型(model)和全尺寸原型(prototype)。
VSG相似理论较好地解决了应变率效应对冲击实验结果造成的影响,但其并未考虑若模型与全尺寸原型使用不同材料制造时,质量相似系数的变化(VSG相似理论认为密度相似系数λρ=1);同时Norton-Hoff公式参数较少、不能准确描述应变率效应的影响,因此还有改进空间。
2 模型修正
本文中给出基于VSG理论的、考虑模型与全尺寸原型使用不同材料制造的修正模型(称之为VSG+方法)。首先引入与应变率相关的Cowper-Symonds公式[8]:
(3)

对于质量相似系数λm有:
(4)
在VSG相似理论中有
(5)
(6)
式中:λv的表达式中包含λv,故须通过迭代方法求解λv。
综上所述,4种相似理论的质量相似系数λm与速度相似系数如表1所示。

表1 4种相似理论质量相似系数与速度相似系数Table 1 Four theories’ mass factors & velocity factors
3 算例验证
为验证上述方法的有效性,引入简化模型、在ABAQUS平台下分别使用已有相似理论和本文中提出的VSG+方法,计算同一缩比尺寸下的冲击实验结果。通过数值模拟得到不同外载条件下模型的凹坑深度,并与全尺寸原型结果做对比。
简化模型为一个四边固支的正方形金属板(边长a=100 mm、厚度H=1 mm)受到直径d=10 mm、质量m=20 g、初速度v0=100 m/s的刚性小球撞击板中心部位,如图1所示。
金属板材料分别选用2024铝合金(对应变率不敏感)和45钢(对应变率敏感),两种材料部分参数如表2所示。

表2 材料参数Table 2 Parameters of the materials
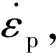

表3 不同材料及比例尺模型的初始外载条件Table 3 Initial conditions for models in different materials & scales
在ABAQUS软件中建立模型并设定各参数,得到4种相似理论数值模拟结果如图2所示。由于尺寸差异,缩比实验结果已按比例尺放大。
从图2(b)、(d)、(f)可看出,由于2024铝合金无应变率效应影响,所以MLT、VSG和VSG+相似理论模型结果均与全尺寸原型结果吻合较好,而Calladine相似理论因其局限性故不适合本算例;从图2(a)、(c)、(e)、(g)可以看出,模型在缩放后由于刚度上升,带来的应变率效应影响也逐渐明显。对比4种理论与全尺寸原型结果可以发现,本文中提出的VSG+相似理论相对于传统相似理论,在建模精度上有了一定提高。
4 结 论
基于VSG相似理论,提出了若模型与全尺寸原型使用不同材料制造时考虑应变率效应的相似理论修正模型:称之为VSG+方法。通过引入与应变率相关的Cowper-Symonds公式,重新计算了质量相似系数与速度相似系数。在与传统相似理论对比后,证明该方法预测精度高于传统理论。
本文中算例均采用典型材料,对于其他应变率敏感程度不同的材料及复杂模型(如复杂结构、复杂初始外载条件等)该理论的适用性,将作为今后研究重点进一步分析。
参考文献:
[1] 沈雁鸣,陈坚强.超高速碰撞相似律的数值模拟验证[J].爆炸与冲击,2011,21(4):343-348.
SHEN Yanming, CHEN Jianqiang. Numerically simulating verification of the comparability rule on hypervelocity impact[J]. Explosion and Shock Waves, 2011,21(4):343-348.
[2] BAKER W E, WESTINE P S, DODGE F T. Similarity methods in engineering dynamics: theory and practice of scale modeling[M]. Amsterdam: Elsevier Science Publishers, 1991.
[3] 谈庆明.高速冲击模型律[M]∥王礼立.冲击动力学进展.合肥:中国科学技术大学出版社,1992:303-320.
[4] 谈庆明.量纲分析[M].合肥:中国科学技术大学出版社,2005.
[5] CALLADINE R C. An investigation of impact scaling theory[M]. London: Structural Crashworthiness, Butterworths & Co Publishers, 1983:169-174.
[6] OSHIRO R, ALVES M. Scaling of structures subject to impact loads when using a power law constitutive equation[J]. International Journal of Solids Structure, 2009,46(18/19):3412-3421.
[7] LEMAITRE J, CHABOCHE J L. Mechanics of solids materials[M]. Paris: Dunod, 1988.
[8] JONES N. Structural impact[M]. New York: Cambridge University Press, 1997.
[9] CHEN Liebin, YANG Jialing. Analytical evaluation of permanent deflection of a thin circular plate struck normally at its center by a projectile[J]. Acta Mechanica Solida Sinica, 2007,20(2):117-122.

