预制缺陷对花岗岩层裂破坏的影响*

邱加冬，李地元，李夕兵，成腾蛟,2，黎崇金

(1.中南大学资源与安全工程学院,湖南 长沙 410083；2.中国瑞林工程技术有限公司,江西 南昌 330031)

层裂破坏是一种由动载荷引起的典型破坏模式。由于自由面或者软弱面的存在，入射的压缩波经由这些结构面时反射成拉伸波，并在两波交汇区叠加产生净拉应力，当净拉应力达到材料的动态抗拉强度时岩体发生层裂破坏。迄今为止，许多学者从理论和实验两方面对层裂破坏现象做了大量的研究。在理论研究方面，早在1977年，Davison等[1]对延性材料的层裂累积损伤进行了理论分析；王泽平等[2]通过建模建立了层裂准则，并对微孔洞、微裂纹的损伤演化过程进行研究；王礼立[3]对Hopkinson杆中的层裂现象也进行了理论分析；白以龙等[4]利用宏观力学和微观损伤之间的关系，开展了层裂现象的理论研究，并以积分的形式提出了损伤函数。在实验研究方面，Weerheijm等[5]利用Hopkinson压杆装置研究了混凝土发生层裂的动态抗拉强度和动态拉伸破坏能量；张磊等[6]利用混凝土通过Hopkinson压杆装置进行了层裂实验研究；Li等[7]、李夕兵等[8]利用自行研制的Hopkinson压杆装置载入半正弦加载波研究岩石的层裂特性，发现在硬岩发生层裂的过程中伴有损伤作用，并探讨了自由面的入射和反射情况，推导出了岩石试件发生层裂的理论公式。但是，以上实验都是针对完整试样所做的层裂破坏研究，由于试件加工困难，很少有学者开展预制缺陷试样的层裂实验。众所周知，在岩石材料内部存在着大量的微裂隙和微孔洞；微孔洞和微裂隙的存在，增大了岩体的初始损伤，影响和改变了岩体内应力的分布，甚至会导致岩体强度大幅降低[9-14]。因此，利用实验和理论的方法，研究缺陷对层裂破坏的影响具有一定意义。本文中，将通过在花岗岩岩杆上预制裂隙缺陷和孔洞缺陷，利用Hopkinson压杆施加冲击载荷，结合高速摄像仪及PFC(particle flow code)模拟技术，研究缺陷对岩体层裂破坏的影响及其破坏机理。

1 层裂破坏理论

在不考虑应力波传播弥散效应的情况下，应力波在岩杆中传播可以视为一维纵波传播。根据应力波传播理论，压缩波经自由面后反射为拉伸波，自由面处应力为零，质点速度加倍，两波交汇处的质点速度为两波质点速度的和[15]。理论上，层裂的产生一般要满足最大拉应力准则，即：当拉伸应力波峰值达到试件的动态抗拉强度时，试件断裂。设由Hopkinson杆冲击入射的半正弦波周期为T，波长为λ，加载应力峰值为σm，并且半正弦波应力时程曲线函数σ(t)表示为：

σ(t)=σmsin(πt/T) 0≤t≤T

(1)

应力波在自由面附近的传播过程如图1所示，其中实线部分为真实的波形，虚线部分为假想半正弦波的另一段。设半正弦波到达自由面的时间t=0，由图1所示，当t≥T/2后，反射应力逐渐大于入射应力，净拉应力区出现，可能发生层裂现象。

假设以净拉应力区出现t=T/2时刻为起始时刻，经过Δt时间后，距自由面δ处净拉应力首次达到动态抗拉强度而发生层裂，则根据文献[8]可以确定初始层裂位置：

(2)

初始层裂发生后，由于初始应力加载过程对岩石材料已经产生了损伤，岩石内部强度大大降低了，剩下试件中已传播过去的部分低强度反射波也可能使岩石再次发生层裂；同时，残余应力的作用也可能造成二次损伤，从而产生二次层裂、三次层裂以及多次层裂现象。

2 实验过程与结果分析

2.1 实验方案与过程

设置了3种花岗岩试件，每组2个，即:完整花岗岩试件、预制条形裂隙花岗岩试件和预制孔洞花岗岩试件。3种花岗岩试样均为截面尺寸为35 mm×35 mm、长度约为118 cm的柱形岩杆。第1组为完整花岗岩试样Int；第2组为预制3条裂隙的花岗岩试样Cra，裂隙位置分别距离自由端25、35和45 cm，裂隙倾角分别为90°、45°、0°，各裂隙的尺寸相同；第3组为预制3个孔洞的花岗岩试样Cir，孔洞中心位置分别距离自由端25、35和45 cm，孔洞半径相同。岩样的密度约为2 920 kg/m3，纵波波速约为4 600 m/s，弹性模量约为62 GPa。

实验在50 mm杆径的SHPB(split Hopkinson pressure bar)水平冲击实验平台上进行，发射腔内放置纺锤型冲头，可以实现半正弦应力波加载[16]，冲头形状如图1所示。实验中采用0.3 MPa恒定气压进行冲击加载，并在一旁架设高速摄像仪同步记录实验过程；高速摄像仪拍摄窗口大小设置为1 024×192，每秒摄像帧数为29 105。

2.2 实验结果

根据前文分析，试件的长度至少要大于二分之一波长方能满足层裂发生的条件，由文献[8]可知入射压缩波的波长约为72 cm，因此试样长度满足要求。据公式(2)计算可得，试样产生首次层裂的范围距自由端为18～36 cm。试样层裂实验结果如表1所示。

结果发现，完整杆首次层裂位置为15.7和18.6 cm，与理论计算范围18～36 cm略有偏差，这与实验的入射加载波并非完全对称的半正弦曲线及材料的离散性有关。实验中采用了高速摄像仪记录试件整个破坏过程，含预制缺陷试样其层裂位置均发生在缺陷附近。如图2 所示，含孔洞及裂隙试样其层裂均发生在预制缺陷附近。由此基本可以推定，孔洞及裂隙等缺陷的存在影响了层裂拉伸面的发生位置。完整杆的破坏过程与文献[8]类似。

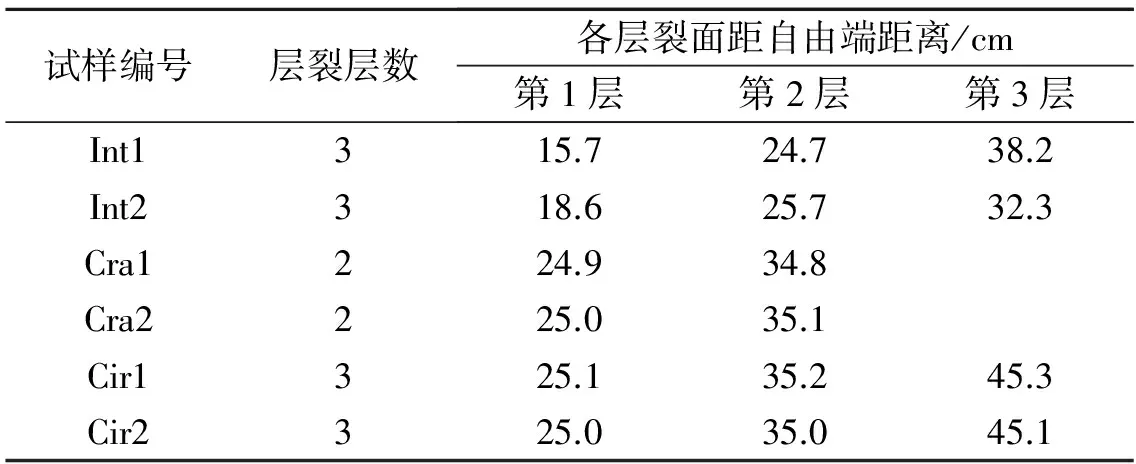
表1 层裂实验结果Table 1 Results of spalling test

2.3 实验结果分析

根据损伤力学的观点[16]，岩石内部的裂纹和缺陷在张应力的作用下会不断活化和发展，促进岩石内部的损伤积累；岩石的损伤量越大，其破坏越容易。本实验中，预制孔洞及裂纹增大了岩石的初始损伤，在孔洞及裂纹段，其动态抗拉强度低于完整段的岩杆，因此在这些缺陷处往往更易破坏。需要注意的是，对于含缺陷的层裂杆，其左端的预制缺陷已经远离了完整杆的初始层裂位置，然而依旧发生层裂，其实是预制缺陷影响了反射拉伸波的传播过程。当反射拉伸波抵达左端预制缺陷时，15.7～18.6 cm区域正处于拉伸波的上升沿，其应力尚未达到此处动态抗拉极限，由于缺陷的存在，裂纹(或孔洞)尖端产生应力集中，此时应力快速上升并先于15.7～18.6 cm处抵达该位置的动态抗拉极限，因此左端预制缺陷处发生了初始层裂。其余缺陷处发生的层裂则是由于层裂杆中残余应力进一步作用的结果[8]。

3 PFC2D模拟对比与分析

采用PFC2D软件反演了层裂实验。模拟的SHPB加载系统与实验一致，其中入射杆等材料参数见文献[16]；通过改变冲头的刚度以获得更短的入射波长，模拟的层裂杆波速为4 754 m/s。图3显示了层裂杆模型, 在其上布置了若干监测圆。经监测可知，层裂杆中入射压缩波波长为58 cm，根据公式(2)计算可得完整杆初始裂纹位置为14.5～29.0 cm。

最终的模拟结果如图4所示，第1层裂位置均在预制缺陷附近，其中预制孔洞模型及预制裂纹模型第2层裂位置分别为20.3～21.3、17.2～18.2 cm。图5为预制孔洞模型部分监测圆的应力时程曲线，图右方为其层裂段的裂纹扩展图像。

如图5所示，入射压缩波及反射拉伸波经过监测圆1时应力均会明显升高，这充分反映了缺陷处应力集中的现象；此外，监测圆1的反射拉伸波上升沿明显比监测圆4的更陡峭，且持续时间更短，这一点恰好印证了第2.3节中所提的预制缺陷对应力波传播的影响, 即预制缺陷处的应力会以更高的速率上升。与实验结果不同的是，由于模拟杆的反射拉伸波上升沿更短，因此在区域20.3～21.3 cm范围处，其拉伸应力率先达到该处的动态抗拉极限，因而区域20.3～21.3 cm最先产生裂纹。但当预制孔洞附近应力达到该处的动态抗拉极限时，由于应力集中的影响，此处的裂纹扩展速度要大于区域20.3～21.3 cm的裂纹扩展速度，因此孔洞周边会先于区域20.3～21.3 cm产生初始宏观断裂面，即第1层裂面，具体见图5；而区域20.3～21.3 cm则在剩余拉伸波的作用下继续发生裂纹扩展，生成第2层裂面。预制裂隙模型与预制孔洞模型类似，但由于前者其反射拉伸波上升沿比后者略缓，持续更长，因此其第2层裂面更靠近自由端。此外，从图2和图5中可以发现，缺陷位置在发生层裂前没有新的裂纹产生。这说明压缩应力波在途经预制缺陷时岩石处于弹性变形或稳定塑性变形阶段，其压缩波对预制缺陷处造成的损伤几乎可以忽略。综上，对比实验与模拟结果，可以明确知道，改变反射拉伸波的上升沿长度，可以有效地改变层裂的破坏过程及位置。反射拉伸波上升沿越长，预制缺陷处越容易发生初始层裂，反射拉伸波上升沿越短，预制缺陷处越不容易发生初始层裂。

4 结 论

(1)预制缺陷的存在改变了应力波在岩杆中的传播。在预制缺陷处由于应力集中，应力波变得陡峭，应力的上升速率加快，其反射拉伸波上升沿会变短。

(2)预制缺陷对花岗岩层裂过程的影响跟反射拉伸波的上升沿有关；上升沿越长，预制缺陷处越容易发生初始层裂，上升沿越短，预制缺陷处越不容易发生初始层裂。若反射拉伸波的上升沿足够长，则初始层裂面发生在靠近自由面的预制缺陷处；如若反射拉伸波稍短，则初始拉裂纹发生的位置则可能偏离预制缺陷位置；同时，预制缺陷还增大了岩石初始损伤，使得预制缺陷处的抗拉强度低于无缺陷处的抗拉强度。因此，预制缺陷处更容易发生层裂破坏。

(3)初始层裂面的位置除了与反射拉伸波的上升沿有关，还与层裂面的裂纹扩展速度有关。预制缺陷处由于应力集中现象，其裂纹扩展速度要快于无缺陷处位置的裂纹扩展速度。因此，预制缺陷较无缺陷处更容易形成初始层裂面。

参考文献：

[1] DAVISON L, STEVENS A L, KIPP M E. Theory of spall damage accumulation in ductile metals[J]. Journal of the Mechanics and Physics of Solids, 1977,25(1):11-28.

[2] 王泽平,恽寿榕.延性材料层裂的数值模拟[J].爆炸与冲击,1991,11(1):20-25.

WANG Zeping, YUN Shourong. Numerical calculations of spallation in ductile solids[J]. Explosion and Shock Waves, 1991,11(1):20-25.

[3] 王礼立.应力波基础[M].北京:国防工业出版出版,1992:46-50.

[4] 白以龙,柯孚久,夏蒙棼.固体中微裂纹系统统计演化的基本描述[J].力学学报,1991,23(3):290-298.

BAI Yilong, KE Fujiu, XIA Mengfen. Formulation of statistical evolution of microcracks in solids[J]. Acta Mechanica Sinica, 1991,23(3):290-298.

[5] WEERHEIJM J, DOORMAAL J C A M V. Tensile failure of concrete at high loading rates: new test data on strength and fracture energy from instrumented spalling tests[J]. International Journal of Impact Engineering, 2007,34(3):609-626.

[6] 张磊,胡时胜,陈德兴,等.混凝土材料的层裂特性[J].爆炸与冲击,2008,28(3):193-199.

ZHANG Lei, HU Shisheng, CHEN Dexing, et al. Spall characteristics of concrete materials[J]. Explosion and Shock Waves, 2008,28(3):193-199.

[7] LI X B, LOK T S, ZHAO J, et al. Oscillation elimination in the Hopkinson bar apparatus and resultant complete dynamic stress-strain curves for rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2000,37(7):1055-1060.

[8] 李夕兵,陶明,宫凤强,等.冲击载荷作用下硬岩层裂破坏的理论和试验研究[J].岩石力学与工程学报,2011,30(6):1081-1088.

LI Xibing, TAO Ming, GONG Fengqiang, et al. Theoretical and experimental study of hard rock spalling fracture under impact dynamic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2011,30(6):1081-1088.

[9] YANG S Q, JIANG Y Z, XU W Y, et al. Experimental investigation on strength and failure behavior of pre-cracked marble under conventional triaxial compression[J]. International Journal of Solids and Structures, 2008,45(17):4796-4819.

[10] WONG L N Y, EINSTEN H H. Systematic evaluation of cracking behavior in specimens containing single flaws under uniaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2009,46(2):239-249.

[11] 李地元,李夕兵,李春林,等.单轴压缩下含预制孔洞板状花岗岩试样力学响应的试验和数值研究[J].岩石力学与工程学报,2011,30(6):1198-1206.

LI Diyuan, LI Xibing, LI Chunlin, et al. Experimental and numerical studies of mechanical response of plate-shape granite samples containing prefabricated holes under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2011,30(6):1198-1206.

[12] 李地元,成腾蛟,周韬,等.冲击载荷作用下含孔洞大理岩动态力学破坏特性试验研究[J].岩石力学与工程学报,2015,34(2):249-260.

LI Diyuan, CHENG Tengjiao, ZHOU Tao, et al. Experimental study of the dynamic strength and fracturing characteristics of marble specimens with a single hole under impact loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2015,34(2):249-260.

[13] 朱晶晶,李夕兵,宫凤强,等.单轴循环冲击下岩石的动力学特性及其损伤模型研究[J].岩土工程学报,2013,35(3):531-539.

ZHU Jingjing, LI Xibing, GONG Fengqiang, et al. Dynamic characteristics and damage model for rock under uniaxial cyclic impact compressive loads[J]. Chinese Journal of Geotechnical Engineering, 2013,35(3):531-539.

[14] 金解放,李夕兵,邱灿,等.岩石循环冲击损伤演化模型及静载荷对损伤累积的影响[J].岩石力学与工程学报,2014,33(8):1662-1671.

JIN Jiefang, LI Xibing, QIU Can, et al. Evolution model for damage accumulation of rock under cyclic impact loadings and effect of static loads on damage evolution[J]. Chinese Journal of Rock Mechanics and Engineering, 2014,33(8):1662-1671.

[15] 张守中.爆炸与冲击动力学[M].北京:兵器工业出版社,1993.

[16] 李夕兵.岩石动力学基础与应用[M].北京:科学出版社,2014.