光学非球面磁性复合流体抛光运动控制及误差分析

, , ,

(上海理工大学 机械工程学院, 上海 200093)

引 言

随着科学技术的高速发展,高精度的光学元件在现代光学系统中扮演着越来越关键的角色。鉴于光学非球面元件具有简化光学系统、提高光学系统精度的优点,其在航空航天、军事、医疗等方面的应用日渐广泛,如激光聚变装置、热成像装置、空间望远镜、数码相机等各类光学仪器[1]。随着光学非球面元件的需求量越来越大,高精度光学非球面元件的加工技术也在逐步完善。抛光作为光学元件冷加工过程中的最后一个步骤,主要有数控小磨床抛光、磁流变抛光、离子束抛光、计算机控制光学表面成型技术等抛光加工方式[2-6]。

20世纪80年代,Kawata等[7]研发了磁流体(magnetic fluid,MF)抛光技术,在磁流体中混入纳米级磁性磨粒,通过磁场辅助控制,对聚丙烯平片进行抛光加工。该磁性流体具有较好的松散性和较高的流变性,但是由于纳米级磁性磨粒的黏度较低,产生的保持力较小,导致加工效率较低,不利于抛光加工。20世纪90年代,Kordonski等将电磁学和流体动力学的理论相结合,克服了在一般磁介质辅助抛光加工中效率较低,面形不易控制等缺点,研发了磁流变抛光(magnetorheological finishing,MRF)技术[8]。磁流变抛光液含有微米级磁性磨粒,黏度较高,加工效率高,但是流变性不够好。21世纪初,Shimada等将含有纳米级磁性磨粒的MF和含有微米级磁性磨粒的MRF混合在一起,研发了一种新型的超精密加工技术磁性复合流体(magnetic compound fluid,MCF)抛光[9]。MCF不仅具有较好的流变性,且黏度较高,磨粒分布稳定性较好,加工效率高,具有良好的抛光性能。为实现MCF抛光的良好效果,在利用MCF进行抛光的加工过程中,抛光运动控制显得尤为重要。抛光轨迹规划作为抛光工艺的重要流程,直接影响着加工效果、加工时间和工件使用寿命。对于传统轨迹规划的研究已经有不少成果,其基本的理论包括:参数线法、截面线法和等残余高度法等[10-13]。但这些方法大部分都是针对车削、磨削工艺进行研究,并没有充分考虑抛光加工的特点。近年来,相关专家针对抛光加工特点建立了很多抛光轨迹规划方法。厦门大学潘日等[14]基于大口径轴对称光学非球面,设计并制造了气囊抛光系统,并对机构进行了仿真分析。吉林大学的曲兴田等[15]对抛光轨迹在非球面上所产生的去除区域的覆盖情况进行了研究,并基于传统的阿基米德螺旋线提出了一种新型的等重叠率螺旋线抛光轨迹规划方法,但是他们的研究内容都未涉及MCF抛光。针对上述问题,本文采用磁性复合流体抛光头,利用工件表面相对抛光头的几何关系,设计了一种直线光栅抛光轨迹,通过仿真模拟进行误差分析,研究得到抛光过程中各个轴进给步长对误差影响的规律,为后续光学非球面磁性复合流体抛光加工中的精度控制起到一定的指导作用。

1 抛光路径规划

1.1 加工路径规划

在抛光加工过程中,抛光头沿着所规划的抛光轨迹进行驻留抛光加工,实现对非球面光学元件表面材料的抛光去除,抛光轨迹规划的优劣直接影响光学元件的抛光面形精度、表面粗糙度和生产效率。通常采用直线光栅式加工轨迹和阿基米德螺旋式加工轨迹,如图1所示。在利用阿基米德螺旋线轨迹的抛光加工过程中,由于其在平面投影上的行距变化,导致轨迹间去除区域的接触面积变化较大,对抛光后工件的表面质量影响较大。因此,本文将采用直线光栅式抛光轨迹对光学非球面元件抛光展开研究。

1.2 加工平台

为实现上述直线光栅式抛光加工轨迹,本文采用五轴精密数控抛光台,其结构如图2(a)所示。光学非球面元件固定在加工平台上,抛光台设有五个驱动电机,每一个驱动电机对应一个轴,驱动电机为X、Y、Z轴提供沿平面的直线运动,为A、C轴提供绕中心的旋转运动。抛光头安装在Z轴导轨上,通过电机驱动抛光头沿Z轴方向直线运动。图2(b)为磁性复合流体抛光头实物图。

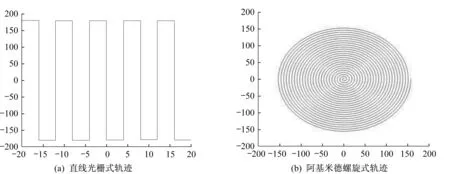
图1 抛光轨迹示意图Fig.1 Schematic of polishing trace

图2 加工系统Fig.2 Polishing system

1.3 路径规划算法

在实际光学系统中,非球面的应用非常广泛。一种非球面方程可表示为

式中:R为非球面曲率半径;k为非球面系数。

基于上述非球面参数方程,采用直线光栅式轨迹规划得到抛光工件上各加工点的坐标P(x,y,z)。根据抛光头自转轴在加工过程中与工件局部抛光点的法线之间的夹角(进动角)始终不变的几何关系[16-17],求出点P(x,y,z)关于工件表面的单位法矢量为

(3)

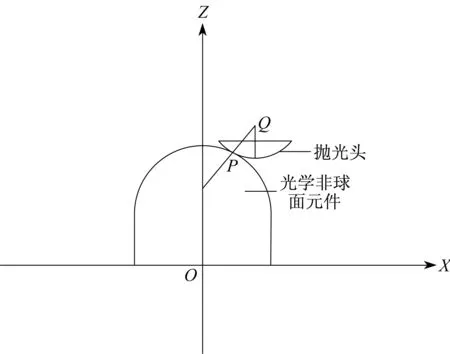
图3 抛光头中心坐标计算Fig.3 Calculation of the center of the polishing head

图3所示。根据几何关系可得工件上抛光点和抛光头中心点的关系。即计算出抛光头中心点Q的位置坐标为

式中r为抛光头部分半径。

最后根据前文所述的直线光栅式的路径规划,即可求出抛光头中心加工轨迹。

2 加工误差分析

为了研究抛光过程中各参数对抛光加工精度的影响,对加工过程中产生的弓高误差进行分析和计算。根据MCF抛光已有研究表明[14],在利用MCF进行抛光的加工过程中,工件的去除轮廓呈W型。在此,假设每个抛光点加工时的驻留时间t都相等,抛光头对工件去除轮廓的一半可近似的看成抛物线方程

y=A(x-x0)2+y0

(6)

其中点P(x0,y0)为工件表面上某个加工点。根据非球面进动过程中进动角ρ不变的原理,加工到下一点P1(x1,y1) 时,抛光头要偏转θ角,与偏转前方程的关系为

(7)

偏转后的方程为

ycosθ+xsinθ=A((xcosθ-ysinθ)-x0)2+y0

(8)

联立式(3),求得两方程的交点坐标为N(xn,yn),连接P和P1点做直线PP1:

(y-y0)(y1-y0)=(x-x0)(x1-x0)

(9)

过N点做NM垂直于PP1,由于在该方向上采用直线插补方式,那么直线PP1就是抛光的实际轨迹,而理想的抛光轨迹是弧线PP1,那么X轴方向上的弓高误差d就可以定义为MN两点的的距离。

图4 X-Z方向误差Fig.4 Error along X-Z direction

根据几何关系得到误差的表达式为

(10)

3 加工模拟与讨论

根据上述抛光加工方法、相关误差分析与计算,对抛光加工过程中所产生的弓高误差进行仿真模拟研究。仿真模拟中,抛光头部分圆弧半径35 mm,非球面工件参数如表1所示。

根据直线光栅式的运动迹规划以及抛光头相对于工件表面的几何关系,仿真模拟出抛光头中心实际加工轨迹,如图5所示。

表1 非球面工件各参数Tab.1 Parameters of aspherical lens

图5 抛光头中心运动轨迹Fig.5 Motion trace of the center of the polishing head

如图6(a)所示,基于直线光栅式的抛光路径规划,其Y方向的弓高误差d随着进给步长的增大而增大。MATLAB仿真结果表明:在Y轴上,当y的值从-180到0时,弓高误差d呈逐渐减小的趋势,在X轴方向上,同一时刻第二条路径的弓高误差减小的趋势比第一条减小的的趋势更大;当y的值从0到180时,弓高误差d呈逐渐增加的趋势。如图6(b)所示,在y等于0附近时,误差降到最低。在y取到最大值180时,误差达到最大。

图6 弓高误差分布Fig.6 Bow height error distribution

通过改变X轴和Y轴的进给步长,经过多次模拟仿真,得到如图7所示数据。当X轴步长为7,Y轴步长分别为5,10,15时,误差最大值分别为93.6,98.77,103.78,最小值为1.24,4.92,10.48,平均值为41.24,41.96,42.85。不难看出,随着Y轴步长的增大,弓高误差d的最大值,最小值以及平均值都在随之增大。

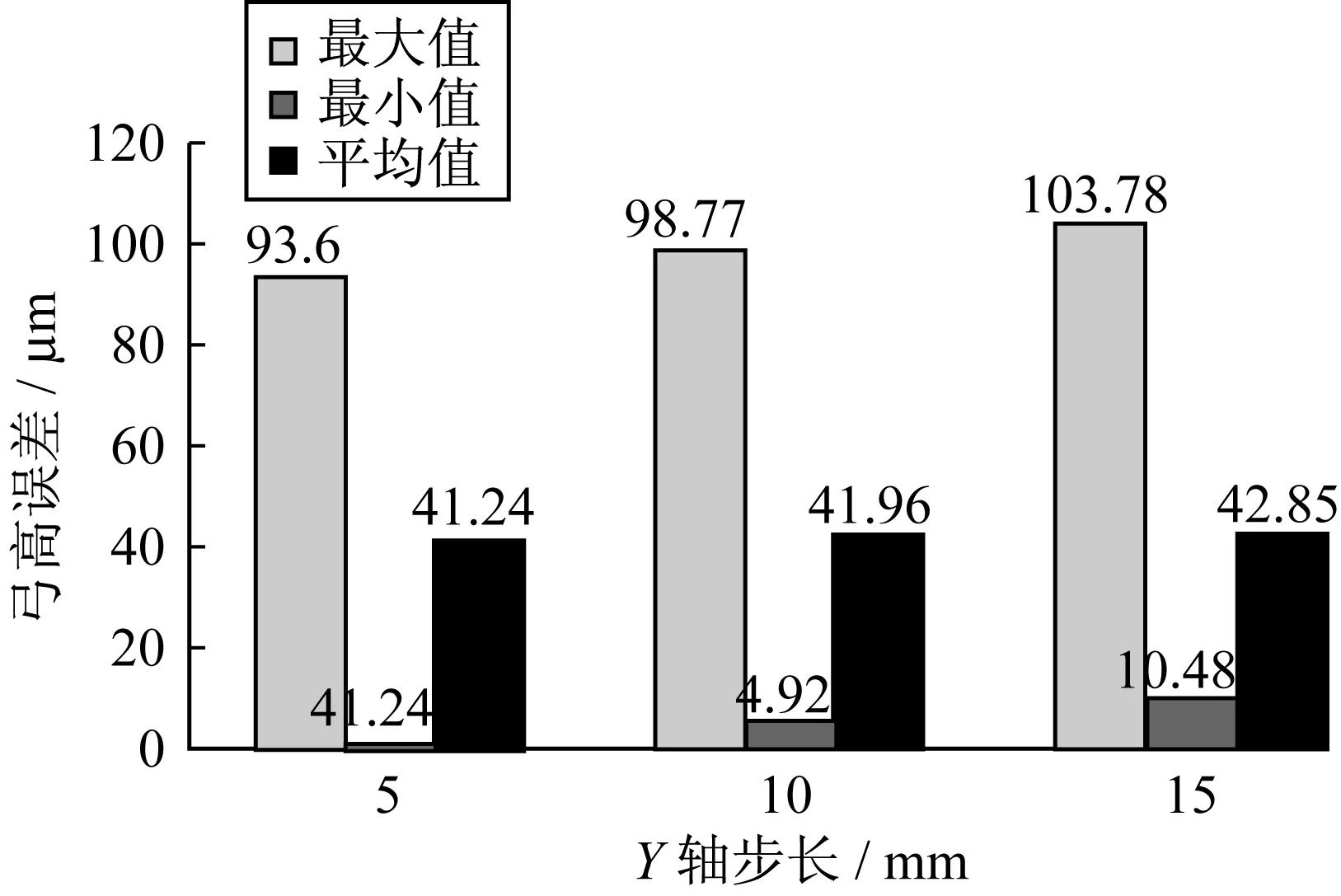
图7 各轴步长与误差关系Fig.7 The relation between the step and the error for differentaxes

4 结 论

(1) 针对非球面光学元件抛光的加工需要,提出采用直线光栅式的加工轨迹对工件进行加工。针对磁性复合流体的特殊性,设计抛光运动控制算法,建立误差模型;根据误差模型计算抛光加工过程中产生的的弓高误差;通过改变不同参数,对工件表面进行误差分析。

(2) 误差的仿真分析结果表明:在YZ平面上,当Y轴上的步长增大时,弓高误差d会随着Y轴上步长的增大而增大。

参考文献:

[1] 杨力.先进光学制造技术[M].北京:科学出版社,2001.

[2] 李铭,张彬,戴亚平,等.多层介质膜光谱调制反射镜的反应离子束刻蚀误差容限[J].强激光与粒子束,2009,21(5):761-766.

[3] 侯晶,许乔,雷向阳,等.基于Marangoni界面效应的数控化学抛光去除函数的研究[J].强激光与粒子束,2005,17(4):555-558.

[4] 王健,鄢定尧,李洁,等.非球面聚焦透镜数控加工技术研究[J].强激光与粒子束,2003,15(10):951-954.

[5] 杨炜,郭隐彪,许乔,等.超精抛光中边缘效应对材料去除量的影响[J].强激光与粒子束,2008,20(10):1653-1657.

[6] 王建,郭隐彪,朱睿.光学非球面元件机器人柔性抛光技术[J].厦门大学学报:自然科学版,2014,49(5):636-639.

[7] 张峰,余景池,张学军,等.磁流变抛光技术[J].光学 精密工程,1999,7(5):1-8.

[8] 张峰.磁流变抛光技术在长春光机所研究进展[J].激光与光电子学进展,2015,52(9):266-272.

[9] SHIMADA K,WU Y B,WONG Y C.Effect of magnetic cluster and magnetic field on polishing using magnetic compound fluid(MCF)[J].Journal of Magnetism and Magnetic Materials,2003,262(2):242-247.

[10] 吴福忠,柯映林.组合曲面参数线五坐标加工刀具轨迹的计算[J].计算机辅助设计与图形学学报,2003,15(10):1247-1252.

[11] FENG H Y,TENG Z J.Iso-planar piecewise linear NC tool path generation from discrete measured data points[J].Computer-Aided Design,2005,37(1):55-64.

[12] GUO H R,WU Y B,LU D,et al.Ultrafine polishing of Blectroless nickel-phosphorus-plated mold with magnetic compound fluid slurry[J].Materials and Manufacturing Processes,2014,29:1502-1509.

[13] 潘日,王振忠,郭隐彪,等.大口径轴对称非球面气囊抛光进动运动建模及控制[J].机械工程学报,2012,48(11):183-190.

[14] 曲兴田,王宏一,樊成,等.等重叠率螺旋线的非球面抛光轨迹规划[J].西安交通大学学报,2015,49(6):126-131.

[15] HE W,LEI M,BIN H Z.Iso-parametric CNC tool path optimization based on adaptive grid generation[J].The International Journal of Advanced Manufacturing Technology,2009,41(5/6):538-548.

[16] 樊文刚,王小椿,姜虹,等.一种开阔自由凹曲面五坐标加工多点刀位算法[J].西安交通大学学报,2010,44(9):69-73.

[17] GUO H R,WU Y B,LU D,et al.Effects of pressure and shear stress on material removal rate in ultra-fine polishing of optical glass with magnetic compound fluid slurry[J].Journal of Materials Processing Technology,2014,214(11):2759-2769.