压剪共同作用下混凝土的损伤演化研究

肖 洋， 彭 刚， 黄 超， 罗 曦， 彭竹君

(1. 防灾减灾湖北省重点实验室(三峡大学)， 湖北 宜昌 443002； 2. 三峡大学 土木与建筑学院， 湖北 宜昌 443002)

随着科学技术的发展，混凝土作为一种重要的工程材料，越来越多地被用于各种复杂结构；许多新的力学现象不断出现，这就要求混凝土破坏机理的研究必须向更深更广的层次发展[1]。

刘军等[2]为了有效描述混凝土的非线性力学性能，在连续损伤力学和不可逆热力学理论框架下，采用显式积分算法建立了一个新的混凝土弹塑性损伤本构模型。Mihai等[3]结合大量的定向断裂模拟力学模型，提出一个独特的纤维钢筋混凝土本构模型(FRC)。Shahsavari[4]为了考虑混凝土在拉伸和压缩中的不同行为，利用共轭的损伤和愈合力表达式，提出了一个研究混凝土材料损伤和愈合现象的本构模型。万征等[5]对Hsieh模型进行了3点改进，并且建立了三维弹塑性本构模型。胡海蛟等[6]进行了5种加载速率下的动态循环加载压缩试验，对混凝土损伤特性及变化规律进行了统计分析。杜成斌等[7]采用混凝土塑性损伤本构模型来描述各相材料的受载力学性能。马怀发等[8]提出了一种适用于复杂应力状态下的双折线弹性损伤模型。Haussler-Combe等[9]基于黏弹性观点，并考虑高加载速率下混凝土的惯性效应，提出了相应的损伤本构模型。

综上可知，对于混凝土损伤模型的提出以及损伤机理的研究大多集中在静态抗压方面，对于混凝土在压剪多种应力状态下的损伤机理分析以及损伤模型的提出还有待展开。为此，本文开展了3种不同加载速率4种不同法向压力作用下的混凝土抗剪试验，提出新的损伤变量计算方法，分析其损伤演化过程，并建立相应的损伤本构模型。

图1 试验设备Fig.1 Loading equipment

1 试验设备及试验过程

1.1 试验设备

本次试验所用设备为三峡大学与长春朝阳实验仪器有限公司联合研制的10 MN大型多功能液压伺服静动力三轴仪(见图1(a))，该设备可进行常三轴混凝土动静力加载试验，最大竖向动、静力荷载值分别为5和10 MN。加载系统有位移、变形与负荷3种控制方式，最大采样频率为104Hz，可实时采集数据并记录。图1(b)为剪切盒。该剪切盒由上下两部分组成，外框架由4根钢柱固定，能保持整体的稳定性。在受到横向剪切荷载作用时，下半部分通过底部螺栓与外框架连接并保持不动，上半部分通过滑槽盒相对外框架做滑移运动。

1.2 试件的加工与处理

试验所采用的混凝土试件设计强度为30 MPa，由水泥、砂、自来水、碎石按一定比例搅拌而成。水泥为P· O 42.5普通硅酸盐水泥；粗骨料是粒径为5～40 mm的连续级配碎石；细骨料是连续级配天然河砂，经过筛分后实测细度模数为2.3，属于中砂。混凝土的配合比为：水175.0 kg/m3，水泥291.0 kg/m3， 细骨料676.9 kg/m3，粗骨料1 257.1 kg/m3。

试验所用混凝土试样为边长300 mm立方体试件，成型方式为钢模浇筑。为了搅拌均匀，本文采取先干拌后湿拌的方法；振捣完成后，将表面磨平处理，室温下放置24 h后拆模；拆模后，将混凝土放入标准养护室养护，保证相对湿度为95%以上，温度为(20±2)℃；28 d后将混凝土移至室外自然养护。

1.3 试验加载过程

①预加载：试件装入剪切盒对中后推入加载设备上。分别向竖向和水平向施加10 kN的荷载。②正式加载：对试件分别施加10, 180, 360, 540, 720 kN的轴向恒定荷载，保持恒定。然后在水平向按照不同的加载速率加载，直至得出包含下降段在内的完整的剪切力-位移(试验所测位移即为后文中的总变形)曲线。③卸载以及后续处理：得到完整的试验曲线后，停止加载，开始卸载，卸载完成后，清理残渣，仪器归位。

2 损伤演化过程分析

2.1 损伤变量的确定

混凝土材料属于弹塑性损伤材料，其能量的损耗不仅表现为与弹性无损材料相比的能量的耗散，也表现为材料内部变形模量的退化和塑性变形的发展[10]。罗曦等[11]对Najar能量法进行了改进。

(1)

式中：Er为任意点卸载再加载的变形模量；E0为混凝土的弹性模量；εe为任意点的弹性应变；ε为任意点的总应变。

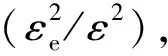
结合本文工况，在混凝土试件完全破坏之前，由于材料自身存在的抗力，在加载到某一变形点卸载后也将存在可以恢复的变形和不可恢复的变形。其中，可以恢复的变形为弹性变形se，不可恢复的变形为塑性变形sp。因此在剪切荷载-变形(Fτ-s)坐标系中，可以等价定义损伤变量如下式(2):

(2)

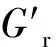
式(2)为本文最终确定的损伤变量计算方法，该式是在假设试件达到某一变形点卸载后再加载不产生新的损伤，即卸载和再加载的应力-变形曲线重合的基础上成立的。

2.2 损伤演化表达式的确定

2.2.1压剪应力状态下混凝土刚度的退化 丁发兴[13]从能量法的角度推导了受压时混凝土的刚度退化与应变能的关系。结合本文工况，在剪切荷载-变形(Fτ-s)坐标系中，可等价得到受剪时混凝土刚度退化与应变能的关系式为：

(3)

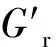
(4)

式中：Fτξ-1和Fτξ分别为某一分段前后的剪切荷载；sξ-1和sξ分别为微分段前后的变形量。

2.2.2压剪受力状态下弹塑性变形 可通过下列公式求得混凝土的弹性变形和塑性变形。

(5)

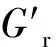
将式(3)和(5)代入式(2)中，即可得到基于理论推导的混凝土在压剪受力状态下的损伤演化表达式：

(6)

2.3 压剪受力状态下的损伤演化过程

由式(6)可得荷载-位移曲线与损伤演化曲线对比图(见图2)，图中荷载采用归一化处理，即纵坐标为Fτ/Fτpk。由于本文设计的工况较多，仅以18 mm/min加载速率为例。

观察图2可以发现，损伤演化可分为3个阶段：①线弹性阶段；②损伤加速变化阶段；③损伤收敛阶段。

图2 不同法向压力下混凝土损伤演化(18 mm/min)Fig.2 Damage evolutionn of concrete

从损伤发展的程度来说，由于损伤变量是定义在[0,1]之间的变量，其最终必定收敛于1，而在损伤变量开始无限趋近于1时，也可近似作为荷载-变形曲线开始平稳变化的收敛点，这些收敛点随法向压力和应变速率的不同而不同。混凝土在受剪状态时，当损伤变量无限趋于1时已经开始发生相对滑移，阻碍剪切变形发展的只是由法向压力产生的摩擦力，此时材料本身已经失去了其结构意义。因此以本文方法计算得到的损伤变量在该点附近趋于最大值是合理的。

损伤发展的速度先增大后减小，对应损伤发展的曲线由凹变凸，且在剪切强度附近时， 损伤发展的速度达到最大，该点往往是曲线凹凸变化的转折点。这是因为混凝土在达到剪切强度之前，一般尚未形成宏观裂缝，损伤发展的速度随着内部微裂隙的增加而增加。当达到峰值应变后，宏观裂缝开始形成，损伤发展的速度也达到最大。在这之后，由于宏观裂缝的存在，混凝土结构开始变得松散，随着变形的继续增大，混凝土内部将沿着这些裂缝继续破坏而很难产生新的裂缝，即本身松散的材料虽然会变得更加松散，但是随着材料应力的下降，在加载速率恒定时，其破坏程度的变化将会变缓，所以材料的损伤速度也会变慢。因此本文方法计算的损伤变量在剪切强度附近速度达到最大也是合理的。

3 损伤演化对比分析

本文试验涉及两种控制因素：法向压力和加载速率。这两种控制因素对混凝土的力学性能有不同的影响，对混凝土受载过程中损伤的发展影响也不相同。下面分别分析法向压力和加载速率对混凝土压剪受力作用下损伤演化的具体影响。

3.1 法向压力对混凝土损伤演化的影响

为研究法向压力对混凝土损伤演化的影响，将相同加载速率，不同法向压力下混凝土的损伤演化过程列出，如图3所示。从图3可以发现，在相同加载速率下，混凝土损伤的发展随着法向压力的增大而滞后，说明法向压力的存在阻碍了损伤的发展。

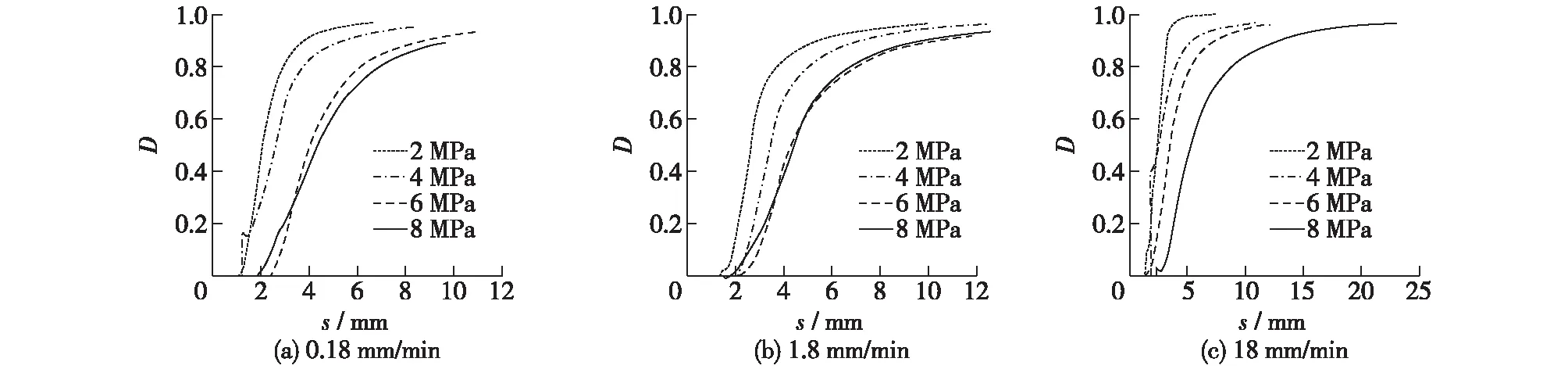
图3 不同加载速率下混凝土损伤演化对比Fig.3 Comparison of damage evolution of concrete under different normal stresses

分析产生这种现象可能的原因如下：混凝土受力过程中，内部裂缝不断产生和扩张，损伤也在不断发展，最终裂缝是沿着剪切破坏面相互贯穿的，剪切破坏面也可以理解为混凝土受力时最薄弱的面，在其余部位虽有裂缝产生，但剪切破坏面的破坏速度一定是最快的，可以理解为混凝土破坏的最短路径，只要裂缝在这条最短路径上完全贯穿，混凝土就已经破坏完全。

从混凝土的损伤发展来看，混凝土在压剪受力状态下，特别是在法向压力较大的时候，损伤可能在除了剪切破坏面的其他部位发展，但是发展的速度没有剪切破坏面上的快，如果以损伤变量的大小去衡量损伤发展的快慢，剪切破坏面上的损伤变量是最大的，它可以代表整个混凝土的损伤发展，所以混凝土损伤的发展就是描述其剪切破坏面的破坏情况，混凝土沿剪切破坏面的完全破坏意味着混凝土的完全破坏，也意味着损伤的完全发展。

在法向压力没有对混凝土造成明显损伤时，法向压力的增大增加了试件的整体受力性能，在其他控制因素不变时，法向压力越大，混凝土受载过程中就会有越多的荷载被传递到剪切破坏面外的其他位置，破坏面上所承担的荷载就会被分担得越多，混凝土整体的损伤演化就会越慢，所以表现为图中所示的损伤发展随着法向压力的增大而滞后的现象。

3.2 加载速率对混凝土损伤演化的影响

为研究加载速率对混凝土压剪受力状态下损伤演化的影响，将相同法向压力，不同加载速率下混凝土的损伤演化列出，如图4。从图4可以观察得到，加载速率对压剪受力状态下混凝土损伤演化影响的规律性没有法向压力对其损伤演化强。整体上，混凝土的速率效应表现为：在法向压力一定时，混凝土的损伤随着加载速率的提高而滞后。

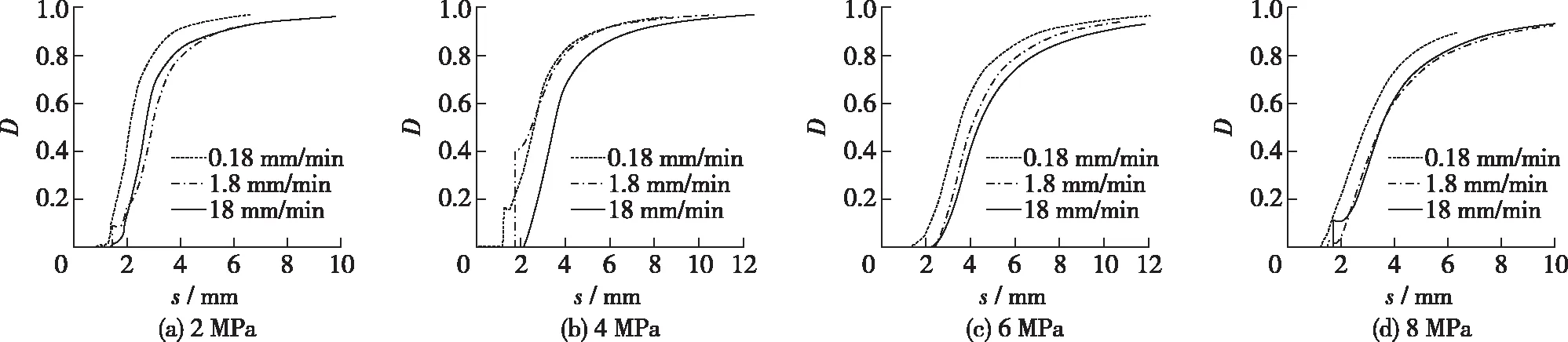
图4 不同法向压力下混凝土的损伤演化Fig.4 Damage evolution of concrete

与法向压力对混凝土损伤演化影响的分析类似，产生这种现象的原因可能是：随着加载速率的增大，损伤来不及在剪切破坏面这一最短破坏路径上发展，而有更多的机会在混凝土的其余部位发展，从而分担了破坏面上的损伤，导致混凝土整体损伤发展的滞后。

4 损伤全曲线描述

4.1 剪切荷载-变形全曲线

早期的混凝土抗剪试验大多只得到了曲线的上升段[14-15]。很早就有学者指出，尽管混凝土的峰值强度是混凝土力学性能中很重要的一个标准，但是从损伤力学的角度出发，在混凝土受载过程的整个损伤演化过程中，峰值点并不具有特殊意义[16]。因此，在混凝土抗剪试验中，全方位地了解混凝土的损伤演化，得到完整的试验曲线十分必要,图5为不同加载速率下混凝土剪切荷载-变形全曲线。

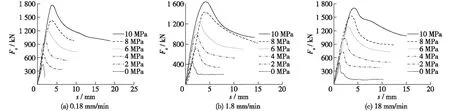
图5 不同加载速率下混凝土剪切荷载-变形全曲线Fig.5 Shear load-deformation curves under different loading rates

由图5可以看出，与混凝土抗压的受力曲线类似，曲线大致可分为3个阶段：①当剪应力比较小时，混凝土处于近似弹性阶段，此时曲线也处于近似线性的阶段；②当剪应力接近剪切强度时，曲线开始表现出比较强的非线性，曲线斜率迅速降低并由正变负；③当变形继续发展，混凝土开始进入应变软化阶段，曲线斜率变化速度也开始放缓，进入平稳期。这也说明，混凝土虽然属于准脆性材料，但在其受剪过程中，破坏并非突然发生，而是一个渐变过程。

4.2 损伤本构模型

与混凝土受压情况类似，受剪情况的损伤曲线分布近似呈S形，大量研究表明，S形的损伤演化曲线近似服从基于经验公式的Weibull统计分布[17]。Weibull损伤模型能够很好地描述混凝土在压剪受力状态峰值强度以前的损伤情况，但是Weibull损伤模型并不能准确地描述峰值强度后的实际情况。因此本文在剪切强度之前采用Weibull统计分布，剪切强度之后在过镇海损伤模型[18]的基础上引入曲线形状控制参数a和b来描述峰后曲线的收敛段。对应损伤变量表达式如下所示。

(7)

式中：spk为任意点的峰值变形；a和b为下降段的形状控制参数，且与法向压力的大小有关，a和b的值可通过拟合得到。

(8)

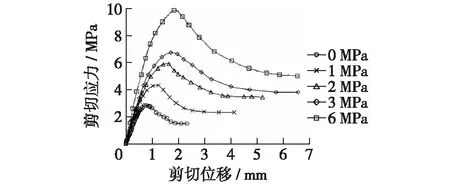
图6 Getdata描点过程Fig.6 Seedling point process

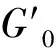
为验证本文全曲线模型在混凝土压剪受力时的适用性，下面将本文模型与文献[19]的数据进行对比，本文通过Getdata软件将文中数据进行再现(见图6)，文中加载速率为0.1 mm/s，法向压力为6 MPa。

文献[19]中的曲线为应力-位移关系曲线，按照式Fτ=τA(τ为剪切应力；A为剪切面面积)将应力换算成荷载后，将得到的荷载-变形试验数据代入本文模型，对峰值点前后的荷载-变形数据进行分段拟合，本文仅以10 mm/s工况下法向压力为0，1，3，6 MPa的拟合结果为例，如图7。

由拟合结果可以发现，文献[19]中抗剪荷载-变形试验曲线通过在峰后引入形状控制参数a和b，可有效解决荷载-变形曲线不收敛的问题，使本文提出的模型与实测荷载-变形曲线整体吻合良好。试验各工况混凝土参数取值见表1。

5 结 语

(1)通过对Najar能量法的改进，提出了一种新的损伤变量计算方法，该方法有明确的物理意义，计算上免去了复杂的积分运算，与实际受载情况吻合较好。

(2)根据损伤演化过程，混凝土在压剪受力状态下的损伤演化可分为线弹性阶段、损伤加速变化阶段和损伤收敛3个阶段。

(3)法向压力对混凝土损伤演化起到显著的影响作用，法向压力的增大减缓了混凝土损伤发展速度，随着加载速率的增加，混凝土损伤的发展有滞后趋势。

(4)本文在试验中得到的剪切荷载-变形曲线包括了上升段和下降段，弥补了之前进行类似试验只得到上升段曲线的不足，并且建立的荷载-变形曲线模型在试验曲线上升段和下降段吻合程度高。

参 考 文 献：

[1] 封伯昊, 张立翔, 李桂清. 混凝土损伤研究综述[J]. 昆明理工大学学报, 2001, 26(3): 21- 30. (FENG Bohao, ZHANG Lixiang, LI Guiqing. A summary of research on damage of concrete[J]. Journal of Kunming University of Science and Technology, 2001, 26(3): 21- 30. (in Chinese))

[2] LIU Jun, LIN Gao, ZHONG Hong. An elastoplastic damage constitutive model for concrete considering unilateral effects[J]. China Ocean Engineering, 2017, 27(2): 169- 182.

[3] MIHAI I C, JEFFERSON A D, LYONS P. A plastic-damage constitutive model for the finite element analysis of fibre reinforced concrete[J]. Engineering Fracture Mechanics, 2016, 159: 35- 62.

[4] SHAHSAVARI H, BAGHANI M, SOHRABPOUR S, et al. Continuum damage-healing constitutive modeling for concrete materials through stress spectral decomposition[J]. International Journal of Damage Mechanics, 2016, 25(6)： 900- 918.

[5] 万征, 姚仰平, 孟达. 复杂加载下混凝土的弹塑性本构模型[J]. 力学学报, 2016, 48(5): 1159- 1171. (WAN Zheng, YAO Yangpin, MENG Da. An elastoplastic constitutive model of concrete under complicated load[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(5): 1159- 1171. (in Chinese))

[6] 胡海蛟, 彭刚, 谢玖杨, 等. 混凝土循环加卸载动态损伤特性研究[J]. 工程力学, 2015, 32(6): 141- 145. (HU Haijiao, PENG Gang, XIE Jiuyang, et al. Study on dynamic behaviour of concrete by cycle loading and unloading conditions[J]. Engineering Mechanics, 2015, 32(6): 141- 145. (in Chinese))

[7] 杜成斌, 江守燕, 徐海荣, 等. 湿筛混凝土试件的静、动破坏数值模拟[J]. 河海大学学报(自然科学版) , 2012, 40(2): 195- 200. (DU Chengbin, JIANG Shouyan, XU Hairong, et al. Numerical simulation of static and dynamic failure of wet-screened concrete specimen[J]. Journal of Hohai University(Natural Science), 2012, 40(2): 195- 200. (in Chinese))

[8] 马怀发, 王立涛, 陈厚群, 等. 混凝土动态损伤的滞后特性[J]. 水利学报, 2010, 41(6): 659- 664. (MA Huaifa, WANG Litao, CHEN Houqun, et al. Mechanism of dynamic damage delay characteristic of concrete[J]. Journal of Hydraulic Engineering, 2010, 41(6): 659- 664. (in Chinese))

[10] 殷有泉. 岩石的塑性、损伤及其本构表述[J]. 地质科学, 1995, 30(1): 63- 70. (YIN Youquan. On rock plasticity, damage and their constitutive formulation[J]. Scientia Geologica Sinica, 1995, 30(1): 63- 70. (in Chinese))

[11] 罗曦, 彭刚, 刘博文, 等. 用改进Najar能量法分析混凝土单轴受压损伤特性[J]. 水利水运工程学报, 2016(5): 103- 108. (LUO Xi, PENG Gang, LIU Bowen, et al. Analysis of damage characteristics of concrete under dynamic uniaxial compression based on improved Najar energy method[J]. Hydro-Science and Engineering. 2016(5): 103- 108. (in Chinese))

[12] GB 50010—2010 混凝土结构设计规范[S]. (GB 50010—2010 Code for design of concrete structures[S]. (in Chinese))

[13] 丁发兴, 余志武, 欧进萍. 混凝土单轴受力损伤本构模型[J]. 长安大学学报(自然科学版), 2008, 28(4): 70- 73. (DING Faxing, YU Zhiwu, OU Jinping. Damage constitutive model for concrete under uniaxial stress conditions[J]. Journal of Chang’an University(Natural Science Edition), 2008, 28(4): 70- 73. (in Chinese))

[14] 董毓利, 张洪源, 钟超英. 混凝土剪切应力-应变曲线的研究[J]. 力学与实践, 1999, 21(6): 35- 37. (DONG Yuli, ZHANG Hongyuan, ZHONG Chaoying. Study on stress-strain curves of concrete under shear loading[J]. Mechanics in Engineering, 1999, 21(6): 35- 37. (in Chinese))

[15] 刘凯华. 再生混凝土压剪复合受力性能的试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. (LIU Kaihua. Experimental study on behavior of recycled concrete under combined compressive and shearing stressses[D]. Harbin: Harbin Institute of Technology, 2014. (in Chinese))

[16] 吴科如. 混凝土在压力荷载下弹性变形和残余变形的变化及其脆性系数[J]. 同济大学学报, 1983(1): 72- 85. (WU Keru. The elastic and permanent deformation fractions of concrete under uniaxial compression and its factor of brittleness[J]. Journal of Tongji University, 1983(1): 72- 85. (in Chinese))

[17] 王春来, 徐必根, 李庶临, 等. 单轴受压状态下钢纤维混凝土损伤本构模型研究[J]. 岩土力学， 2006, 27(1): 151- 154. (WANG Chunlai, XU Bigen, LI Shulin, et al. Study on a constitutive model of damage of SFRC under uniaxial compression[J]. Rock and Soil Mechanics, 2006, 27(1): 151- 154. (in Chinese))

[18] 过镇海, 张秀琴. 混凝土在反复荷载作用下的应力-应变全曲线[J]. 冶金建筑, 1981(9)： 14- 17, 13. (GUO Zhenhai, ZHANG Xiuqin. Full stress-strain curve of concrete under cyclic loading[J]. Metallurgical Construction, 1981(9)： 14- 17, 13. (in Chinese))

[19] 王怀亮, 田平. 动态压剪作用下碾压混凝土强度和变形研究[J]. 水利与建筑工程学报, 2016, 14(2): 18- 24. (WANG Huailiang, TIAN Ping. Strength and deformation characteristics of RCC under dynamic compressive-shear loading[J]. Journal of Water Resources and Architectural Engineering, 2016, 14(2): 18- 24. (in Chinese))