博观约取 厚积薄发
——浅谈“分数的认识”的教学
浙江宁波市鄞州区邱隘镇中心小学(315100) 陈 飞
在区青年教师研讨班的一次教材研读活动中,我整理的内容是“分数与小数的认识及运算”,在整理的过程中发现,如果没有对教材进行充分的挖掘与深刻的研读,课堂教学再华丽也是徒然的。作为数学教师,如果没能在课堂上真正理解并呈现数学教学的本质,那么,教学设计越是精致,课堂实施越是完美,给学生带来的唯有更加严重的“南辕北辙”。秉着“对教材的挖掘再充分一些、再深刻一些”的原则,我对“分数的认识”的教学进行了深入的研究。
一、尽博观,积累厚识,探求分数本质
何谓分数?这是教师教学前首先要思考的问题。
分数概念就是起源于“分”,在表达平均分结果的时候,遇到了分的结果比1还要小的情况,这时候只用自然数显然是不够的,于是引进了分数,这时的分数是把一个物体平均分成若干份,表示这样的一份或几份,这就是分数的初步认识。后来分数扩展到可以把一个物体平均分,如果把一些物体、一个计量单位等看成一个整体,平均分后,其中的一份或者几份,可以用自然数来表示,但也可以理解为是这个整体的几分之一或几分之几。
至此,分数的概念就完整了,但这还没能体现引进分数的本质:分数是一个不同于自然数的新数,又与小数、百分数、比、除法和概率等概念有着紧密的联系。因此定义分数时,还可以再充分一点,再深刻一点,以a/b为例,至少可以从下列六种角度来讨论分数的意义。
(1)平均分:把单位“1”平均分成b份,再取出a份。例如:将一个蛋糕切成五等份,取出其中的三份。
(2)部分与全体的比较:全体为b时,a是b的部分。例如:“一块蛋糕的一半”或“三个苹果中的两个”。
(3)小数的另一种记法。例如:0.6=3/5。
(4)除法运算的结果:表示a除以b的商。例如:“5÷3”的结果是“5/3”。
(5)比的意义:两个自然数a和b,b≠0,把比值a/b叫作分数。例如:“一根6米的竿子”和“一根3米的竿子”的长度比为1/2。
(6)测量:用来测量一个不满一个单位量的量的数值问题。例如:1米和2米的中间到底有多长呢?结果是1又1/2米。
二、巧约取,小贴金泥,另辟教学蹊径
教学,需要一种智慧。我渴望拥有它,但它却总是与我若即若离,因为它不可言说、无以言传。然而,在对“分数的认识”的教材进行深刻研读后,我却有了新的领悟——教学的智慧在于对教材的把握。
1.要联系自然数来初步认识分数
在“分数的初步认识”这一课中,学生第一次建立分数的概念。教材编排有以下特点:(1)由一个物体组成单位“1”。如一个月饼、一个纸片等。(2)只出现常见的分母比较小的分数(分母一般不超过10)。(3)只出现真分数以及分子分母相等的假分数。(4)不正式定义分数,只通过直观手段建立初步的分数概念。
考虑到学生的年龄特点和思维能力,教师不必对分数的本质挖掘过深,只要让学生理解分数的“面积模型”即可:三年级学生只要“知其然”,等到五年级再“知其所以然”。因此,课堂结构一般是:
(1)巧设生活情境,引出分数。
(2)借助整数经验,创造分数。
(3)在丰富的数学活动中深化认识,理解分数。
[案例1]情境与冲突
出示主题情境图(图略),并引导学生思考:
①把4个苹果平均分给2人,每人分得几个?
②把2瓶矿泉水平均分给2人,每人分得几瓶?
(结合学生的交流,教师揭示:每份分得同样多,数学上叫作“平均分”)
③把1个蛋糕平均分给2人,每人分得多少?
(学生在交流中自然得出“一半”)
④每人分得的苹果、矿泉水可以用以前学过的数来表示,那“一半”该用怎样的数来表示呢?
(学生交流各自的想法,教师结合学生的交流,揭示课题:认识分数)
“平均分”是初步认识分数的基础,在分配苹果、矿泉水和蛋糕的过程中,教师巧妙地唤醒了学生“平均分”的经验,为学生初步认识分数做好了铺垫。同时,随着问题的发展,学生的思维视角能从“自然数”中突围,实现了由自然数到分数的和谐过渡。
[案例2]探索与建构
(1)直观感知,初步认识
①引导:我们把蛋糕平均分成了几份?“一半”是其中的几份?
揭示:“一半”正好是2份中的1份,可以用1/2来表示。
②追问:这一份(指2份中的1份)是蛋糕的1/2,另一份(指2份中的另1份)呢?
小结:把一个蛋糕平均分成2份,每份都是它的1/2。
(2)动手操作,深化认识
①出示一张长方形纸,引导学生思考:怎样表示它的1/2呢?
②出示操作要求:先折一折,再把它的1/2涂上颜色。
③在学生表示出长方形纸的1/2后,组织学生交流各自的表示方法。
④深究:折法不同,涂色部分的形状也不同,为什么涂色部分都是长方形的1/2?
小结:不管怎样对折,只要平均分成2份,每份都是长方形的1/2。
(3)观察判断,拓展认识
出示如图1所示四个图形,引导学生思考:下列图形中,哪些图形的涂色部分可以用1/2表示?

图1
小结:只有把一个图形平均分成2份,每份才是这个图形的1/2。
教师在教学1/2时如此浓墨重彩、层层推进,其意图在于:这样认识1/2,学生便可以很好地建构分数的概念,从而形成较强的知识迁移能力,为自主认识其他的几分之一做好铺垫。在每一层次的教学中,教师让学生反复理解“把一个物体平均分成2份,每份就是这个物体的1/2”,这里的“2份”和“每份”都是学生已经熟识的自然数,能借助自然数帮助学生理解1/2,是教师对三年级学生思维水平有了准确把握。
2.分数的意义教学要从单位“1”的意义建构着手
“分数的意义”这一课的主要特点是:(1)单位“1”变成了一些物体;(2)正式定义分数,用规范化的数学语言建构分数的意义。
教学时,重点突出单位“1”的抽象性,通过建构分数的“面积模型”“集合模型”和“数线模型”,使学生理解单位“1”作为标准量和单位量的内涵;不仅要学生用形式化和规范化的数学语言表达对分数意义的认识,更应引导学生深入建构每一个具体分数的意义。课堂结构一般为:(1)回顾面积模型(一个物体);(2)建立集合模型(一些物体);(3)感受数线模型(分数的本质);(4)深化对分数意义的理解。
[案例3]分数的“面积模型”→“集合模型”
师(往学生面前一站):认识张老师吗?能用自然数来表示张老师吗?
生1:用“1”表示。(板书:1)
师:除了人以外,还有什么也可以用“1”来表示呢?
生2:一个班级也能用“1”来表示。
师:这时候的“1”和我们一年级的“1”一样吗?
生3:一年级的“1”表示的是一个代号,这时候的“1”是一个整体。
师:3个苹果能用“1”吗?怎么能让3个苹果看起来就是“1”?
生4:放在一个盘子里。
师:把3个苹果看作一个整体,就能看成“1”。
师:那6个、9个、18个苹果……也能看成“1”吗?
生5:能。
师:一旦把3个苹果看作“1”,那6个苹果应该看作几?
生6:2。3 个苹果是“1”,6 是 2 个“1”,就是“2”。
师(出示12个苹果):有4个这样的“1”,就是几?
生7:4。
师:有5个这样的“1”,一共是几个苹果?
生8:15 个。
师:3个苹果看成的“1”就成了一个计量单位。在数学上,可以称作单位“1”。
单位“1”的含义应建立在对“1”(面积模型)的理解上,因此教师由表示一个物体的自然数1引入,过渡到可以表示一些物体(集合模型)组成的整体的自然数“1”,“1”的内涵获得了一次重要的拓展和提升。那么如何帮助学生实现由“1”向单位“1”的实质性跨越?教师将学生置身于实际计量的数学活动中,让学生通过观察和比较认识到,无论把什么看作“1”,只要包括几个这样的“1”,就可以用“几”来表示,丰富了学生对单位“1”内涵的认识。
[案例4]建构分数的数线模型
师(在学生认识了3/4后,出示数轴):你能在数轴上找到3/4吗?
生1:把0~1之间的线段平均分成4份,取其中的3份,就是3/4。
师(出示图2):1/4和2/4都能在这上面找到位置。那2在哪里?
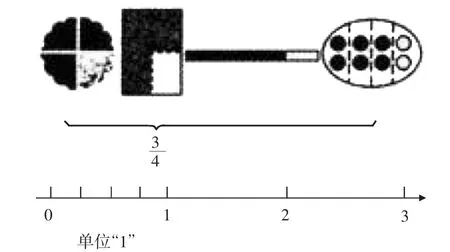
图2
生2:把数轴延长,在2个“1”这么长的地方,就是2。
师:如果不满单位“1”,就用分数来表示,如果满了单位“1”,有几个单位“1”就是几。
师(在学生认识了更多分数后):认识了这些分数的含义,那它们在刚才的数轴上也能找到相应的位置吗?如果我们还是把0到1这一段看作单位“1”(出示图3),1/3又该如何表示呢?
图3
生3:很简单!只要把它平均分成3份,再表示出这样的1份就行了。
师:既然1/3表示的就是0到这里的一段,有时我们就直接用这一个点(指第一个三等分点)来表示1/3。
师:既然这样,那2/5、5/8又分别在什么位置呢?在自己的作业纸上找一找、标一标。
三年级学习分数,是建立在面积模型(部分-整体)的维度上,但随着分数学习的不断深入,在五年级就应该让学生体会到分数的集合模型和数线模型,实现由分数的无量纲性到有量纲性转变。上述片段中,教师在学生认识3/4的同时,借助数轴这个载体,通过将3/4纳入数轴体系,使学生直观地认识到,和1、2、3等自然数一样,分数同样可以在数轴上找到相应的位置。随后教师又进一步引导学生认识1/3、2/5、5/8等分数,建构每一个分数的含义,在数轴上找到这些分数相应的位置,这是将分数的集合模型上升到数线模型,在抽象层面上建构起一般分数的意义。
三、细回味,满树幽香,教材研读味无穷
苏轼曾语:“博观而约取,厚积而薄发。”这句话对于数学教学同样适用。只有通过别人的实践和自己的亲身体验,去芜存精、去伪存真,才能获取有价值的知识。
1.博观而约取,领会知识内涵
教材研读要着眼于对文本内涵的挖掘,从而抓住知识的本质。张奠宙教授说过:“数学教学设计的核心是如何体现‘数学的本质’‘精中求简’‘返朴归真’,呈现数学特有的‘教育形态’,使得学生高效率、高质量地领会和体验数学的价值和魅力。”因此,在教学之前,教师首先要明确教材在教学中的重要性,深入探究知识的本质。
2.厚积而薄发,发展深度课堂
教师在领会知识的内涵后,才能更好地梳理教学体系,把教材中零碎的数学知识进行归类,明确知识在体系中的地位,分析不同学段的教学要求,确定每节课的具体目标,并且落实到位。
教师用数学的魅力,轻轻地打开学生心灵的窗户,让学生可以洞察这门学科的奥秘。这一切,正是因为教师有了知识“博观”——对文本的多角度理解,课前“厚积”——能在不断变化的课堂情境中以不同的教法解读教材,学生才能自然地理解数学知识,感受数学思想方法,走向有深度的课堂。
综上所述,一名优秀教师的成长不是靠华丽的教学设计,而是得益于他们对教材的深刻解读。我们想要教得清楚,想要学生学得到位,就要在尊重与学习教材的基础上深入理解教材,弄清教材内容前后的联系,领会教材中每一个知识点呈现的意图,使学生获得更深、更广、更高效的知识。

