主成分分析应用(I)——主成分回归分析

胡良平

(1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029 *通信作者：胡良平，E-mail：lphu812@sina.com)

1 概 述

1.1 基本概念

本期《基于SAS与R软件的主成分分析》一文介绍了“单组设计多元定量资料”这种特殊的数据结构，并指出：分析这种数据结构的统计分析方法占全部多元统计分析方法中的绝大部分，主成分分析法是其中一个最基本的方法，可以被灵活地运用于多重回归分析之中。

1.2 何为主成分回归分析

主成分回归分析(the Principal Components Regression Analysis)是将作为自变量的多个定量因素转换为全部互相独立的综合变量(即主成分变量)，构建定量因变量依赖所求得的“全部主成分变量”变化而变化的回归模型，这样完成的多重线性回归分析被称为“主成分回归分析”[1]。

1.3 为何要使用主成分回归分析

由于在经典统计学中，要求自变量互相独立，此时，才可以构建多重线性回归模型。当自变量之间存在多重共线性时，经典统计学理论认为：所建立的多重线性回归模型的质量就不高，甚至可能是不能解决实际问题或违反专业知识的回归模型(指某些回归系数的正负号不符合基本常识和专业知识要求)。消除自变量之间的多重共线性关系，有多种具体方法，本文拟采用“主成分回归分析法”。

1.4 问题与数据结构

【例1】为推算成年人的收缩压(SBP,mmHg)，研究者测量并收集了50名成年人的年龄(age)、身高(height,inches)、体质量(weight,pounds)和体质量指数(BMI)。结果见表1[1]。试以SBP为因变量、其他四个变量为自变量建立多重线性回归模型。

表1 50名成年人的测量数据

续表1：

33397321027．7113534776213825．2415035397323030．3412536406917025．1012637446211521．039938276114026．4511439297322029．0313940786311019．4915041626520834．6111242227112517．4312743376417630．2112544387219526．4513645226514023．3010846796112523．6215647246214626．7010848326714122．0810549427019227．5512150426818528．13126

1.5 对数据结构的分析

在表1中，单从数据角度看，基本满足进行多重线性回归分析的要求；但严格地说，题目中并没有交代清楚：这50例受试者是从一个什么样的总体中以什么方式抽取的，更具体的疑问是：他们在收缩压(SBP)这个指标上是否具有同质性？若有些人属于“严重高血压患者”、有些人属于“中度高血压患者”、有些人属于“轻度高血压患者”、有些人属于“临界高血压状态人群”，还有些人属于“正常血压人群”，而且，这50人组成的样本不是从各群体中按相同比例随机抽取的，那么，他们就不具有同质性，此资料也就不值得进行任何统计分析。

在本文中，假定资料具有同质性，且确定样本含量也是有一定依据的。再结合医学专业知识，人的年龄、身高、体质量和体质量指数确实对收缩压有一定的影响(严格地说，应找全所有可能影响收缩压的因素，应确定一个同质的研究总体，按不少于80%的效能从此总体中随机或分层随机抽取足够大的样本含量)，笔者仅从统计建模角度展开下面的论述。

2 探索性分析

2.1 构建基本的多重线性回归模型

基于本刊2018年第1期《基于经典统计思想实现多重线性回归分析》一文介绍的方法，利用下面的SAS程序构建基本的多重线性回归模型：

data a1;

input id age height weight bmi sbp;

cards;

(此处输入表1中50行6列数据)

；

run;

proc reg data=a1;

model sbp=age height weight bmi;

run;

因篇幅所限，输出结果从略。从输出的结果中可看到：截距项无统计学意义，需要将其删除后重新拟合多重线性回归模型。在前面的过程步程序的“model语句”的“；”之前增加一个选择项“/NOINT”，得到的结果表明：weight和BMI两个自变量都无统计学意义，若将它们都从回归模型中删除，则可被利用的自变量就很少了。于是，考虑这4个自变量之间是否存在某种线性关系，从而导致不够理想的结果出现。

2.2 对全部自变量进行共线性诊断

采用下面的SAS过程步程序对全部自变量进行共线性诊断：

proc reg data=a1;

model sbp=age height weight bmi/noint collin;

run;

【SAS主要输出结果】

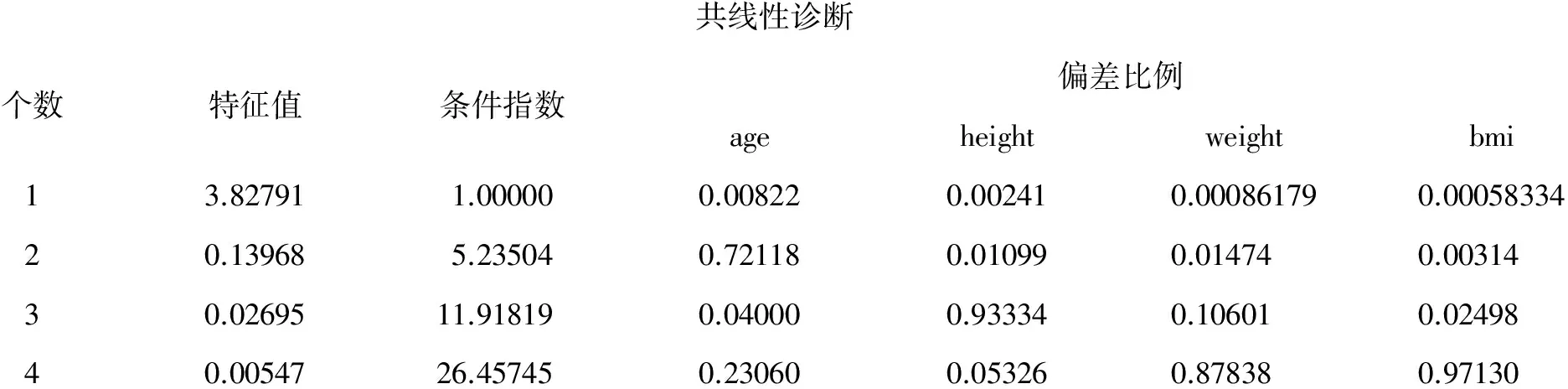
共线性诊断个数特征值条件指数偏差比例ageheightweightbmi13．827911．000000．008220．002410．000861790．0005833420．139685．235040．721180．010990．014740．0031430．0269511．918190．040000．933340．106010．0249840．0054726．457450．230600．053260．878380．97130

由上面的最后一行后4列的计算结果可知：weight和BMI的“偏差比例”都大于0.5，说明它们之间确实存在较严重的共线性关系。

3 主成分回归分析

3.1 对全部自变量进行主成分分析[2]

所需要的SAS过程步程序如下：

proc princomp data=a1 out=b1 prefix=z;

var age height weight bmi;

run;

此程序输出结果为：产生4个主成分变量z1-z4及其取值，这是中间结果(暂不呈现了)存储在名为b1的数据集中。

3.2 基于z1-z4作主成分回归分析

所需要的SAS过程步程序如下：

proc reg data=b1;

model sbp=z1-z4;

run;

输出结果(此处从略)中包含无统计学意义的变量，需要采取变量筛选方法淘汰掉无统计学意义的主成分变量。所需要的SAS过程步程序如下：

proc reg data=b1;

model sbp=z1-z4/selection=backward sls=0.05;

run;

输出结果(此处从略)表明：此模型的复相关系数R平方=0.3262，残差方差=200.41879。

3.3 仅对有共线性的自变量进行主成分分析

所需要的SAS过程步程序如下：

proc princomp data=a1 out=b2 prefix=z;

var weight bmi;

run;

此程序输出结果为：产生2个主成分变量z1-z2及其取值，这是中间结果(暂未呈现)存储在名为b2的数据集中。

3.4 基于独立自变量age、height和主成分变量z1-z2作主成分回归分析

所需要的SAS过程步程序如下：

proc reg data=b2;

model sbp=age height z1-z2/selection=backward sls=0.05;

run;

输出结果(此处从略)表明：此模型的复相关系数R平方=0.3470，残差方差=194.24348。

3.5 改变筛选变量的策略

前面筛选自变量时假定需要保留“截距项”，下面假定不需要保留“截距项”，所需要的SAS过程步程序如下：

proc reg data=b2;

model sbp=age height z1-z2/noint selection=backward sls=0.05;

run;

【SAS主要输出结果】

方差分析源自由度平方和均方F值Pr>F模型37408772469591285．20<0．0001误差479031．34023192．15618未校正合计50749908

变量参数估计值标准误差II型SSF值Pr>Fage0．522340．114394006．5347820．85<0．0001height1．516260．0695091470476．02<0．0001z13．209081．44250951．010674．950．0309

此模型的复相关系数R平方=0.9880，残差方差=192.15618。

3.6 基于两种途径得到的主成分回归模型的比较

前面获得两个二重回归模型拟合效果接近，第2个比第1个稍好，因R平方更大、残差方差更小，但它们之间的差别很微小；第3个模型为三重线性回归模型，残差方差192.15618比第2个模型的194.24348略小，然而，R平方=0.9880比第2个模型的0.3470更大。

4 慎用主成分回归分析

4.1 通过改变筛选自变量的策略来提升回归模型的拟合效果

一般来说，不要急于采取主成分回归分析方法，而应首先考虑改变筛选自变量策略来提升模型拟合效果。就本例而言，直接采取前进法、后退法和逐步法筛选全部自变量，并分别假定模型中包含“截距项”与不包含“截距项”。

经尝试，包含截距项时，三种筛选方法得出的结果一致，结果如下：模型对资料的拟合效果不太好，R平方=0.3723，残差方差=186.73058。

经尝试，不包含截距项时，三种筛选方法得出的结果一致，结果如下：模型对资料的拟合效果较好，R平方=0.9883，残差方差=186.89456。这个结果比上面基于主成分回归分析得到的最好结果更好。

4.2 通过引入派生变量和改变筛选自变量的策略来提升回归模型的拟合效果

可以引入4个自变量的平方项和交叉乘积项(共10项)，再加上原先的4个自变量，总共14个自变量参与自变量的筛选。筛选时，仍采取前面提及的策略，即基于包含“截距项”与不包含“截距项”且分别采用前进法、后退法和逐步法筛选，得到最好的结果如下：

方差分析源自由度平方和均方F值Pr>F模型874477093096761．06<0．0001误差425137．61575122．32418未校正合计50749908

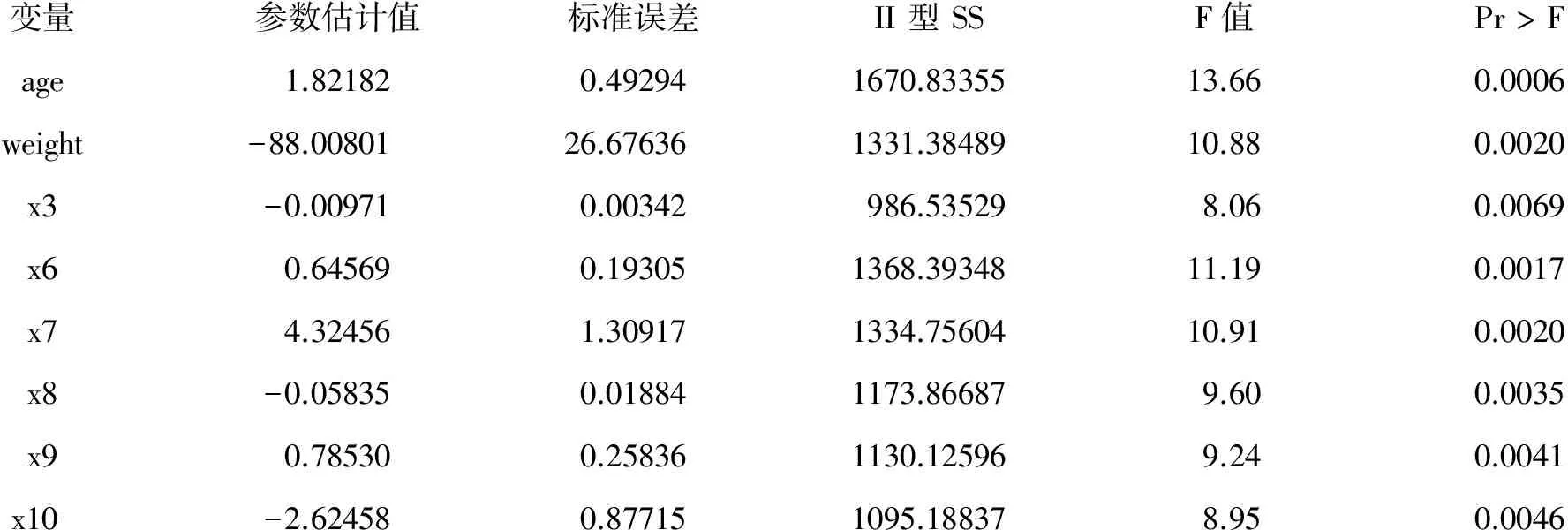
变量参数估计值标准误差II型SSF值Pr>Fage1．821820．492941670．8335513．660．0006weight-88．0080126．676361331．3848910．880．0020x3-0．009710．00342986．535298．060．0069x60．645690．193051368．3934811．190．0017x74．324561．309171334．7560410．910．0020x8-0．058350．018841173．866879．600．0035x90．785300．258361130．125969．240．0041x10-2．624580．877151095．188378．950．0046

以上结果表明：模型对资料的拟合效果很好，R平方=0.9931，残差方差=122.32418。

前面的“x3、x6～x10”分别代表：x3=age*weight、x6=height*weight、x7=height*bmi、x8=weight*weight、x9=weight*bmi、x10=bmi*bmi。

这个模型对资料的拟合效果要好于前面未引入派生变量的最好模型的拟合效果。

值得注意的是：weight的回归系数为“-88.00801”，这个“负值”表明：体重越重的人收缩压(SBP)越低，这似乎不符合临床专业知识。但应当注意：模型中还包含了“x6=height*weight”和“x9=weight*bmi”这两项，它们的系数都为正，且乘积的结果是很大的数值。所以，在整体上，此模型是不违反临床专业知识的。

4.3 小结

显然，上面的最后一个多重线性回归模型中的很多“项”之间存在严重的多重共线性关系，若对它们采取“主成分分析”提取主成分变量，再进行主成分回归分析，最终结果如下：

(1)基于全部8个变量(age,weight,x3,x6-x10)构建主成分回归模型且假定包含截距项，R平方=0.5931，残差方差=129.30182。

(2)基于全部8个变量(age,weight,x3,x6-x10)构建主成分回归模型且假定不包含截距项， 无法构建多重线性回归模型。

(3)基于6个有共线性关系的变量(weight,x6-x10)产生的6个主成分变量再加上2个独立变量(age和x3)构建主成分回归模型且假定包含截距项，R平方=0.6095，残差方差=1560.03944。

(4)基于6个有共线性关系的变量(weight,x6-x10)产生的6个主成分变量再加上2个独立变量(age和x3)构建主成分回归模型且假定不包含截距项，R平方=0.8892，残差方差=1731.12908。

以上的结果都不如仅引入派生变量但不采取主成分变量构建的多重线性回归模型的拟合效果好。故笔者建议：一般应慎用主成分回归分析。

类似文献[3]的资料都可能用到多重线性回归分析，当然，也就有可能会用到主成分回归分析。经验表明：应慎用主成分回归分析，而在引入派生变量的前提下，采取不同的筛选自变量的策略，有可能获得比较理想的多重线性回归模型。

参考文献

[1] 胡良平. 面向问题的统计学——(2)多因素设计与线性模型分析[M]. 北京: 人民卫生出版社, 2012: 215-228, 264-272.

[2] 胡良平. 面向问题的统计学——(3)试验设计与多元统计分析[M]. 北京: 人民卫生出版社, 2012: 19-39.

[3] 赵巍峰, 彭敏, 谢博, 等. 健康教育对精神分裂症患者病耻感影响的持续性[J]. 四川精神卫生, 2017, 30(6): 519-523.