基于图像处理的伺服系统精度测量方法及装置
庞增拴,李欣
(河北省机电一体化中试基地河北石家庄050081)
电机伺服控制系统在空间通信和军事技术领域有着广泛的应用,是雷达、光电精密跟踪系统、光电测控仪等设施不可或缺的组成部件[1]。这几年随着科学技术的变革,现代化的发展对伺服控制系统的精度要求越来越高。因此,除了不断提升传感器、伺服电机等部件的使用性能之外[2-4],优化的精度测量方法和误差补偿也变得越加重要。
国内外相关技术人员也提出很多电机伺服控制系统定位精度测量方法,如使用千分尺、读数显微镜、线纹尺、激光双频干涉仪和光栅测量等[3-5],这些测量方法需较高的人力和物力,仅能靠经验与肉眼观测得到结果,精度不够。因此提出了一种以ARM为控制核心,搭建了激光发射模块和图像采集模块的测试平台。
1 测试平台组成及测试原理
测试平台主要由PC机,被测电机,激光发射模块,十字分划板和图像采集及处理模块五部分组成。被测电机主要包括航向和俯仰两个运动方向。激光发射模块采用PL-6505D激光器,激光光斑大小为1 mm,光束发散度为0.5mrad;图像采集及处理模块使用arm5728控制器,通过USB摄像头完成图像采集及处理。测试平台主要组成框图如图1所示,测试平台构成部件如图2所示。
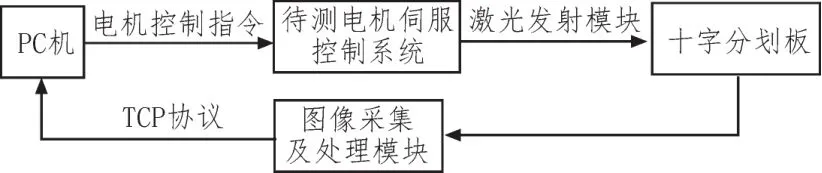
图1 测试平台组成框图

图2 测试平台构成
激光发射模块固定在与电机动子无机械接触固件上如图2(a)所示,这样可大大减少测量误差[6]。十字分划板安装在距激光发模块为L距离处,测试原理如图3所示。

图3 电机伺服控制系统测试原理
根据图3可知:

其中,L为激光发射模块和十字分划板的距离,α为伺服系统的俯仰角,h为激光光斑移动距离。伺服控制系统俯仰运动,激光光斑呈现在十字分划板上为竖直位移,而航向运动则呈现为水平位移。两个方向的测试原理相同,文中则以俯仰运动为例,说明了测试原理及方法。由式(1)可知,根据光斑的移动距离,可得到伺服系统的俯仰角度,从而把角度测量转化为位移测量。
2 亚像素中心提取测量方法
2.1 十字分划板亚像素中心点提取
经过图像采集系统得到的测试图像如图4所示,根据测试原理可知得到十字分划板中心和激光斑中心的距离,即可得伺服电机的俯仰角度。

图4 测试图像
现有的十字中心提取方法主要分为像素级和亚像素级两大类[7-9]。像素级提取的中心最少为像素宽,不能满足测量的精度要求,仅适用十字中心位置的粗略估计[10-12]。文中针对十字线条纹图像为直线这一特征,提出了一种十字线条纹亚像素中心的提取方法。预处理条纹图像去除噪声,局部区域二值化;利用最小二乘直线拟合和重心法,精确提取十字线亚像素中心。
1)图像二值分割
由于后续处理将利用十字线的二值信息,故需分割条纹图像,获取十字线条纹目标区域。分析图像可知,条纹目标与背景较分明,固采用最大类间方差法(OTSU)进行图像二值化,然后采用形态学开闭可平滑二值十字条纹目标的边界、去除孤立点、填充细小空洞等,处理后图像如图5所示。
2)十字线亚像素中心的精确提取
分别利用四条直线对十字线的竖线条纹和横线条纹进行直线拟合。本文中将对竖线条纹的两条边界直线求取为例进行说明。根据二值化分割后的图像可知,竖条纹每行像素的的二值图分布规律如图6所示。对每行进行扫描时,得到图像的二值化由1变为0的点集为:

图5 二值分割图像

该点集合构成竖条纹的左边界直线。同理图像的二值化由0变为1的点集为:
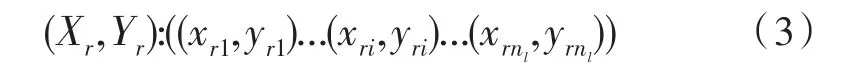
该点集构成竖条纹的右边界直线。

图6 十字竖条纹像素二值分布规律
利用最小二乘法分别拟合两条直线得[13]:

其中,
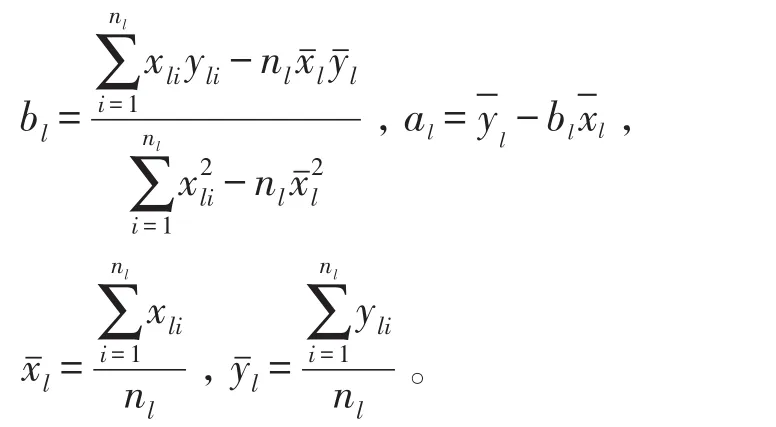
同理可得到右边界直线。
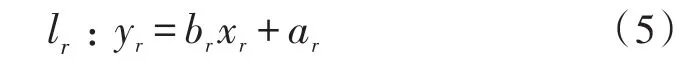
利用上述算法得到十字线的四条边界线。得到四条直线的交点分别为(xlu,ylu),(xru,yru),(xld,yld),(xrd,yrd)。根据4个交点利用重心法求得十字线的亚像素中心点坐标(x,y)为:

2.2 激光光斑的亚像素中心点提取
理想点光源成像的光斑灰度近似符合二维高斯分布并具有较好的对称性,因此可以基于矩形提取窗口进行激光光斑的亚像素中心点提取[14-18]。
1)矩形提取窗口获取
利用上文提到的二值化和形态学方法获得激光光斑的区域如图8所示。再利用闭合区域提取方法获得光斑的外接矩形如图9所示。该矩形左上角像素坐标为(x1,y1),右下角像素坐标为(xn,yn),像素(xi,yi)处的灰度值为f(xi,yi)的窗口,即为高斯拟合中的矩形提取窗口。

图7 光斑区域

图8 光斑的外接矩形
设矩形窗口内像素灰度分布近似符合二维高斯函数
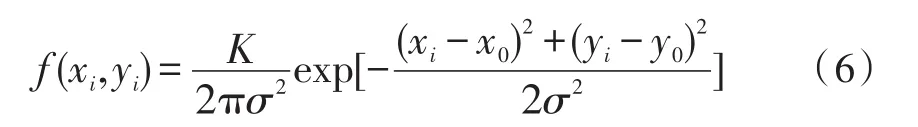
式中 (x0,y0)为光斑中心坐标,σ为高斯函数的均方差,与物距、焦距、离焦量和光圈大小有关,K为能量系数[17]。对式(6)两边同时取对数得:

从而可得方程组

最小二乘解为:
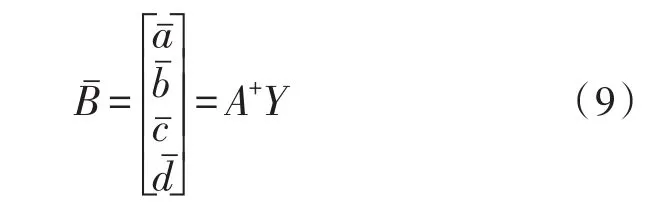
其中,表示B的最小二乘解,A+为矩阵A的广义逆矩阵,进一步得

(0,0)即为激光光斑的亚像素中心点坐标。
3 实验结果及分析
把测试平台放在高精度二维转台上,用PC机控制电机俯仰方向旋转一定角度θ,通过采集十字分化板图像,在arm5728控制器上利用十字分化板和激光中心提取算法分别提取亚像素中心(x,y)和,试验平台如图9 所示。
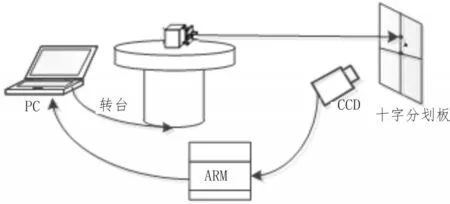
图9 试验平台
通过标定摄像机的内参和外参,根据(x,y)和像素距离可得实际距离h。代入式(1)得到电机测量角度θ′。然后旋转转台使(x,y)和重合,记录旋转角度(-θ″),则θ″即为使用高精度转台测量的电机旋转角度。测量数据见表1。
根据19组测量数据可知,使用该方法测得的角度最大绝对误差≤7.2″具有较高的测量精度。在测量过程中L的测量精度也将影响角度测量,因此使用高精度的激光测距仪测得L的大小,也会有效的减少测量误差。

表1 实验测试数据统计表
4 结论
为了满足电机伺服控制[18-19]的高精度要求,针对电机标定和精度测量提出了一种基于图像处理的亚像素电机伺服控制精度测量方法。采用最大类间方差法进行图像二值化,利用形态学开闭方法去除杂波,获取十字分化条纹和激光光斑的有效面积信息。再采用图像灰度信息分布规律对图像进行横列扫描和重心相结合的方法提取十字分化的亚像素重心;并且采用最小二乘高斯曲面拟合法提取激光光斑的亚像素中心。算法有效结合了十字条纹的宽度信息和激光光斑能量分布信息,降低了噪声引起的局部灰度极值对中心定位精度的影响,弥补了十字分化不对称性引起的误差。实验结果表明,本文算法具有较高的测量精度。因此利用该方法对伺服控制系统进行标定和精度测量简单,有效。
参考文献:
[1]王文毅.激光跟踪伺服控制系统研究[D].北京:北京信息科技大学,2015.
[2]丁仁杰,吴志波,邓华荣,等.高自动化卫星激光测距系统研究与设计[J].激光与红外,2017,47(9):1102-1107.
[3]翟少雄,王长胜,谭立,等.空间高精度扫描伺服系统的驱动控制[J].光学精密工程,2016,24(5):1104-1111.
[4]刘炯钟,林敏,郭斌.嵌入式伺服压机系统高精度位置控制的研究[J].组合机床与自动化加工技术,2015(4):91-93.
[5]李莹莹,张志毅,袁林.线结构光光条中心提取综述[J].激光与光电子学进展,2013,50(10):9-18.
[6]HENRIKSEN S J,BETZ R E,COOK B J.Digital hardware implementation of a current controller for IM variable-speed drives[J].IEEE Trans on Industrial Application,2014,35(5):1021-1029.
[7]邹焱飚,王研博,周卫林.焊缝跟踪应用的线激光视觉伺服控制系统[J].光学精密工程,2016,24(11):2689-2698.
[8]董巧玲.不同误差影响模型下总体最小二乘法在多元线性回归中的应用研究[D].太原:太原理工大学,2016.
[9]Wedowski R D,Atkinson G A,Smith M L,et al.Dynamic deflectometry:A novel approach for the on-line reconstruction of specular freeform surfaces[J].Optics&Lasers in Engineering,2012,50(12):1765-1778.
[10]刘常杰,李斌,郭寅,等.焊接机器人实时引导中光条快速提取算法研究[J].激光技术,2015,39(5):642-647.
[11]Popovic B M,Bandur M V,Raicevic A M,et al.Different methods for fingerprint image orientation estimation[J].Proc of 20th Telfor,2012:20-22.
[12]苏小勤,熊显名.快速线结构光中心提取算法[J].计算机应用,2016,36(1):238-242.
[13]张秋佳,赵玉华.基于加权插值算法的激光光斑中心检测[J].激光与红外,2016,46(1):81-84.
[14]陈和,杨志浩,郭磐,等.激光光斑中心高精度定位算法研究[J].北京理工大学学报,2016,36(2):181-185.
[15]孙立环,赵霄洋,高凌妤,等.基于亚像素定位技术的激光光斑中心位置测量[J].激光技术,2017,41(4):511-514.
[16]王杰飞,刘洁瑜,赵晗,等.一种改进的激光光斑中心亚像素定位方法[J].激光技术,2015,39(4):476-479.
[17]WANG Zh J,ZIOU D,ARMENAKIS C,et al.A comparative analysis of image fusion methods[J].IEEE Transactions on Geoscience &Remote Sens⁃ing,2012,43(6):1391-1402.
[18]王韬,马训鸣,刘霞,等.电液力伺服系统模型参考控制方法[J].西安工程大学学报,2015,29(5):589-593.
[19]李抗,张蕾,李鹏飞,等.交流永磁同步伺服电机的参数自整定模糊PI控制[J].西安工程大学学报,2015(3):325-331.
[20]覃秋松,麦云飞.模糊工程PID在气动位置伺服中的应用[J].电子科技,2015,28(11):104-109.

