一种融合协同过滤和用户属性过滤的混合推荐算法
曹俊豪,李泽河,江龙,张德刚
(云南电网有限责任公司教育培训评价中心,云南昆明650000)
目前,云南电网年培训人次达6万,具有规模大、内容覆盖面广、专业多、专业性强等特点,如何根据每个用户行为数据对用户推送其感兴趣的项目(如设备知识点)成为培训中一个难题。于此,本次研究中提出了一种融合协同过滤和用户属性过滤的混合推荐算法,即移动端通过用户行为收集用户习惯行为信息,利用该算法对用户的基本行为习惯进行分析整合,结合用户的兴趣为其推荐对应的项目服务。在平台“基于数字编码的移动学习管理平台”中的实验及实际应用中表明,本文算法在对比其他推荐算法具有较优的信息推荐效果[1-2]。
1 混合推荐算法
1.1 协同过滤下邻居用户的寻找
当前,信息推荐领域算法种类繁多,一般常见的是协同过滤算法。协同过滤算法是通过分析所有用户对物品的偏好,发现与当前用户爱好相似的邻居用户群,根据发现的相似用户群对当前的匹配用户进行信息推荐;另一种类型是基于项目的协同过滤算法,这种算法是在分析物品与物品之间相似度后,根据当前用户爱好为其推荐相似的物品[13-14]。本文中混合算法是一种基于用户的算法,通过对不同用户之间的相似度进行匹配,推荐给用户相似邻居的个性化推荐内容。本文考虑到用户的兴趣会随时间不断发生变化,提出了时间热度这一概念,并对相似度计算进行优化。
1)用户评分矩阵
系统中需要在得到匹配用户对项目的兴趣评分的基础上,利用评分值反映用户对项目的兴趣值。评分值范围一般在1~5,为概似值范畴,相对的评分值越高,即表示当前匹配用户对项目的兴趣度越大[15]。设 I1、I2、...、IM 为系统的项目,U1、U2、...、UN为系统的用户,将用户对项目的评分填入对应的矩阵单元中,即可得到用户-项目评分矩阵,如表1所示。

表1 用户-项目评分矩阵
2)时间热度
对于传统的算法,其在当前用户的邻居寻找时,对时间方面并无涉及,但时间概念对用户的兴趣具有较大的影响,若将这一因素忽略往往导致推荐的内容同用户需求之间产生较大的变化。为了寻找对推荐结果更有价值的相似用户,考虑用户近期访问的项目比早期访问过的项目更能反映用户兴趣,本文在相似度计算公式里面加入了时间热度因素,避免了在相似度计算时忽视了时间概念对用户兴趣的影响,增加寻找相似用户的可信度。
时间热度是指用户访问项目的时间新鲜度,访问时间离当前时间越近则新鲜度越高,时间热度就越高,反之亦然。设Dui表示用户u访问项目i的时间与用户u最早访问系统任一项目的时间间隔(在数据库中有相应的时间记录),定义时间热度函数WT(u,i),它是一个和Dui相关的函数值。在本文研究中,为了能够对访问项目的重要性进行重点突出,其通过设计一种关于Dui的递减函数来对其进行表示[16],即对于 Dui>Duj,有 WT(u,i)≥WT(u,j)。时间热度函数计算公式如下:

上述公式为线性函数,其中Lu指的是用户u在进行推荐系统使用时的时间跨度,也就是该用户最早访问的项目同当前需要访问项目之间的时间间隔,a∈(0,1)称为权重增长指数。
3)Pearson相关系数的优化
计算用户相似度的方法有很多,最常见的一般是Pearson相关系数。用户集U、项目集P以及给定的用户所对项目的评分矩阵R(如表),ra,p表示了匹配用户a对兴趣项目p的评分,`ru表示匹配用户u对兴趣项目P评分的平均值,则用户a和用户b的相似度表示如下:

在传统的算法中,当其在对当前用户兴趣进行分析时,往往会将时间这一影响因素考虑在外,而在文中通过Pearson系数[17]对算法进行了改善,从而能够为用户推荐更加具有价值的内容,改善的公式内容为:
从公式(3)中可以看出,引入时间热度之后,在计算a和b的相似度时,用户历史中近期的兴趣将会反映更加充分。利用优化后的公式(3)可计算出当前用户与其余用户的相似度,在得到似度的基础上可以用Top-N原则票选出当前匹配用户的N位邻居用户。
但是通过本文提出的改进的用户相似度计算公式(公式(3))计算得出的相似用户集合,其集合中也有可能会存在与目标用户兴趣差异很大的相似用户,所以在一般情况下并不能对用户群中匹配的所有的相似用户都可以有很好的信息推荐效果。由这样的相似用户产生的推荐准确率是比较低的。之所以会存在这种现象,主要是由于评分矩阵比较稀疏的缘故导致的,接下来要做的就是要再次过滤掉这类相似度比较低的用户。
1.2 用户属性过滤下相似度低的邻居用户滤除
要求在用户属性过滤下对计算出的相似度比较低的邻居用户进行滤除,需要得到对应用户的特征矩阵。而计算对应特征值则需要对用户的一系列属性进行特征提取,提取方法广泛,在得到了对应用户的特征矩阵后,即可计算出相应用户与用户之间的相似度。
1)建立用户的特征矩阵
一个用户可有多种属性,本文提取其中较能反应用户特征的7种属性来构建用户特征矩阵,分别是:工种、学历、工龄、归属部门、性别、岗位、技能等级。特征矩阵如表2所示。

表2 用户特征矩阵
2)计算用户之间的相似度
用户特征属性包括工种、学历、工龄、归属部门、性别、岗位、技能等级,则用户u的特征属性可以用向量 UAttru=(au1,au2,au3,au4,au5,au6,au7)来表示。其中,从u1到u7分表代表以上用户特征属性。对于数值属性,如工龄,根据实际经验本文规定若二者工龄相差超过3,则认为二者不同;对于分类属性,例如工种、学历、归属部门、性别、岗位、技能等级则采用原始值。若用户u和用户v的第i个属性相同,我们令USimUAttr(u,v,i)=1,否则USimUAttr(u,v,i)=0。用户u和v的相似度可以用下面的公式来计算[18]。
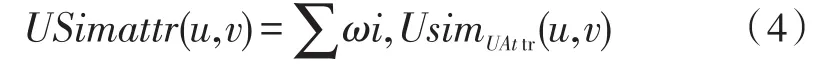
式中:为第i个属性的权重,所有属性的权重值相加为1。
1.3 推荐步骤的描述
融合协同过滤和用户属性过滤的混合推荐算法其具体实现流程有以下几个步骤:
1)由用户访问项目的具体时间,根据公式(1)计算时间热度。
2)对于待推荐用户,利用前文中改进过的相似度计算公式(3),得到当前匹配用户与其他用户的相似度,结合Top-N原则票选出由N位匹配用户所组成的相似邻居用户集。
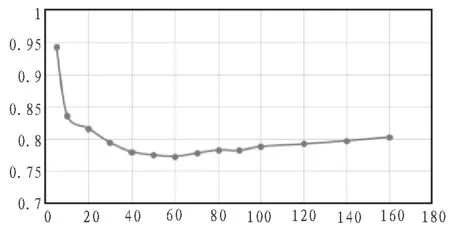
3)依据本文前面介绍特征矩阵建立方法建立对应用户的特征矩阵,并且可以通过公式(4)得到的N位邻居用户逐一与当前匹配用户的相似度比较分析,根据相似度大小由小到大对匹配用户N位邻居用户整理,经过排序分析,以票选方式选择出最终的对应M位可信邻居(M 4)匹配用户a对项目p的预测评分ra,p的计算公式如下: 5)在得到预测的基础上,由Top-N方法票选出最终能代表当前匹配用户最佳信息推荐项目的项目集合。 数据稀疏度是指不包含数据的单元与总单元的相对百分比,其计算公式如下: 式(6)中:A表示已包含数据的单元数,P表示总单元数。本文采用自《基于数字编码的移动学习管理平台》产生的数据集,包含897个用户对122个项目的8 600条兴趣评分,评分的值为1到5,根据公式(6)可计算出数据稀疏度为0.921 4。在数据集中随机性抽取其中百分之八十作为训练集,另外百分之二十作为测试集。利用所抽取的百分之八十的训练集中的数据和本文所属的算法来算出测试集中所有单元的预测评分,对比测试集中的实际评分可对算法的推荐质量进行分析。 在实验中的评价指标采用平均绝对误差(MAE)。实验中计算得出的测试度量集合中的测试用户对项目的预测评分一般与实际的用户评分有一定的偏差,而MAE可以通过这种偏差对度量结果的准确性进行度量,一般而言,MAE测试度量值越大,推荐质量越低;越小,推荐质量越高,也即推荐可信度越高。具体的MAE计算公式为: 预测的用户评分集pi为{P1,P2,…PN},对应实际的用户评分集qi为{q1,q2,… ,qN}, 为了验证文中混合推荐算法的有效性,分别对传统的协同过滤算法(UserCF)和本文混合推荐算法(Hybrid Recommendation Method,HRM)进行了对比实验,实验的结果如图1~2所示。图横坐标为K值(用户数),纵坐标为评价指标MAE值。 1)从两个图可得出,基于协同过滤算法的MAE值在整个k值区间都要大于本文混合推荐算法的MAE值,MAE越小,表示推荐质量越高,由此可说明本文所述的混合推荐算法在整体推荐精准度上优于传统的协同过滤算法。 2)从两个图可得出,当k>60后,随着k值的增加,两种算法的MAE值都有所增加,但是基于协同过滤算法的MAE值的增长速率明显高于基于本文混合推荐算法的MAE值的增长速率,MAE值增长速率越低,则表示推荐稳定性越好,由此可说明本文所述的推荐算法在稳定性上要优于传统的协同过滤算法。 图1 基于协同过滤算法的MAE值 图2 基于本文混合推荐算法的MAE值 相关参数关系分析和信息推荐方法对比实验表明,本文所支持的融合协同过滤和用户属性过滤混合推荐算法在一定程度上是行之有效的算法,相对于传统经典的协同过滤算法一定呈上缓解了数据稀疏矩阵所造成的用户相似度不高的问题,其推荐范围更广,推荐可信度也更高,推荐效果更优。但是本文提出的算法还存在一些其他问题,例如在用户属性过滤下比较对应匹配用户与用户之间相似度值时,对匹配用户的不同属性特征在计算模型中的权重如何分配等问题还有待进一步的深入研究。 参考文献: [1]刘庆鹏,陈明锐.优化稀疏数据集提高协同过滤推荐系统质量的方法[J].计算机应用,2014,24(12):88-91,95. [2]张亮.基于协同过滤与划分聚类的推荐算法研究[D].长春:吉林大学,2014. [3]王雪.协同过滤推荐算法的改进研究[D].鞍山:辽宁科技大学,2016. [4]一种适应于e-Learning环境的复杂推荐算法[J].环球信息,2014,17(2):271-284) [5]温梅.个性化推荐中基于贝叶斯网络的用户兴趣模型研究[D].武汉:华中师范大学,2013. [6]李克潮,蓝冬梅.一种属性和评分的协同过滤混合推荐算法[J].计算机技术与发展,2013,23(7):116-119,123. [7]郝丽燕,王靖.基于填充和相似性信任因子的协同过滤推荐算法[J].计算机应用,2013,33(3):834-837. [8]陈彦萍,王赛.基于用户-项目的混合协同过滤算法[J].计算机技术与发展,2014,24(12):88-91,95. [9]许智宏,王宝莹.基于项目综合相似度的协同过滤算法[J].计算机应用研究,2014,31(2):398-400. [10]李克潮,梁正友.适应用户兴趣变化的指数遗忘协同过滤算法[J].计算机工程与应用,2011,37(6):226-243. [11]杨秀萍.融合用户评分和属性相似度的协同过滤推荐算法[J].计算机与现代化,2017,33(7):16-19. [12]刘欣.面向社会化媒体的内容推荐若干关键技术研究[D].北京:北京邮电大学,2015. [13]王三虎,王丰锦.融合用户评分和属性相似度的协同过滤推荐算法[J].计算机应用与软件,2017,34(4):305-308,321. [14]Xiangyu Tang,Jie Zhou.稀疏数据下的动态个性化推荐[J].IEEE知识与数据工程汇刊,2013,25(12):2895-2899. [15]李梁,张海宁,李宗博,等.融合用户属性的协同过滤推荐算法在政府采购中的应用[J].重庆理工大学学报:自然科学,2015,31(1):76-81. [16]纪科.融合上下文信息的混合协同过滤推荐算法研究[D].北京:北京交通大学,2016. [17]邹永贵,望靖,刘兆宏,夏英.基于项目之间相似性的兴趣点推荐方法[J]计算机应用研究,2012,29(1):116-118,126. [18]陈庚午.混合推荐算法在云计算平台的研究与应用[D].沈阳:中国科学院研究生院(沈阳计算技术研究所),2016.
2 实验以及结果分析
2.1 实验数据与度量

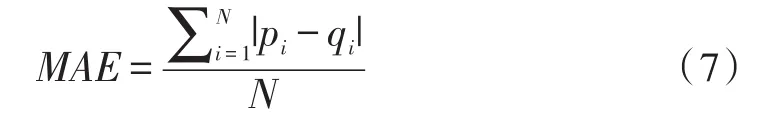
2.2 结果分析

3 结束语

