基于混沌和神经网络的图像加密研究
王晋 丘嵘 王祥

摘 要:为保证信息传输过程中图像的安全性和可靠性,文中提出了一种基于混沌和神經网络的图像加密算法。该算法应用改进型Henon映射产生的混沌序列,通过BP神经网络进行训练,得到基于混沌神经网络的非线性序列。利用该隐式的非线性序列,结合图像加密算法,对图像进行加密。经实验测试和安全性分析,该加密算法安全性高,稳定性较好。
关键词:混沌;神经网络;改进型Henon映射;序列训练;图像加密
中图分类号:TP309.7 文献标识码:A 文章编号:2095-1302(2018)04-00-03
0 引 言
随着互联网技术的高速发展,人们越来越重视信息安全问题,其中图像作为信息传递的重要载体,对安全性和保密性要求尤其高。传统的加密算法(如DES或者RSA)虽然可以用于图像加密,但效率不高,易被破解,因此寻求一种安全高效的图像加密技术十分必要[1]。分析目前几种常见的图像加密方法,如图像像素空间置乱、灰度值变换、空间位置与灰度值双重变化[2],这种只通过像素置乱对图像加密的方法易被统计学分析所破解,而图像灰度值变换主要利用密钥产生伪随机序列,因此其核心是生成难以破解的伪随机序列。
混沌系统对初值极为敏感,其产生的混沌信号能够生成伪随机序列,可作为保密系统中的密钥流[3]。但由于混沌映射参数和状态模拟精度的限制,在一定程度上,混沌序列表现出局部线性和强相关等缺点,因此单纯利用混沌序列产生的伪随机序列进行加密存在一定的局限性[4]。神经网络[5]是一种高度非线性动力学系统,K.Aihara等人首次将生物神经元的混沌行为概念引入神经网络理论中,并用来预测复杂非线性系统。文献[6]提出了一种基于Hopfield混沌神经网络的图像加密算法,设计了一种基于混沌控制参数的置乱扩散结构;文献[7]针对流密码对明文变化不敏感的缺陷,提出了一种基于细胞神经网络(CNN)的图像加密算法。这些算法启发我们利用神经网络来训练混沌序列(本文选择了改进型Henon混沌映射[8])。经训练后得到的非线性序列不仅具有更加随机和无序性等特点,还保持了混沌系统的敏感性,增强了抗线性攻击和差分攻击的能力[9]。本文根据此训练结果,结合图像加密算法,设计了一种基于混沌神经网络的图像加密算法,经实验分析得,该算法加解密效果好,密钥敏感性强,抗统计分析能力强,提高了图像信息的安全性。
1 混沌映射选择
Henon混沌系统的系统方程见式(1):
当b=0.3,a∈[1.07,1.4]时,系统处于混沌状态。但该Henon映射产生混沌的参数区间较小,为了增大混沌参数区间,本设计采用改进型Henon映射[7]产生训练前样本,改进的Henon系统方程见式(2):
当a=3.3,b=0.3时,系统处于混沌状态。图1(a)~(c)分别为改进型Henon映射的参数分岔图和吸引子图,可以得出系统在混沌状态时的具体参数范围。当a=3.3时,系统的混沌范围为b∈[-0.027,0.56];当b=0.3时,系统的混沌范围在a∈[1.8,2]∪[2.4,2.7]∪[3,3.6]区间。通过Jacobi方法计算可得,该系统的李雅普诺夫指数为L1=1.172 0,L2= -3.061 6。相比较Henon映射的李雅普诺夫指数,改进后的系统李雅普诺夫指数明显提升,映射范围加大,系统的不可预测性更强,可采用该混沌序列作为神经网络的非线性序列训练样本。
2 神经网络对混沌序列的训练
将x,y的初始值代入式(2),同时,取a=3.3,b=0.3,循环迭代M×N次后,产生非线性混沌序列{x(i)},{y(i)},本文取{x(i)}作为神经网络的输入训练样本。采用三层BP神经网络对改进型Henon混沌序列进行训练,即将x (1), x(2),…, x(N)构成的序列作为神经网络的输入,以产生x(N+1), x(N+2), x(N+n)构成的序列,利用训练后的序列进行加密。本文采用的神经网络训练参数设置如下:输入层到隐含层神经元权值设置为1,隐含层到输出层权值设置为wi=0.5,神经网络中阈值设置为0(简化网络结构),激励函数采用Laguerre函数:
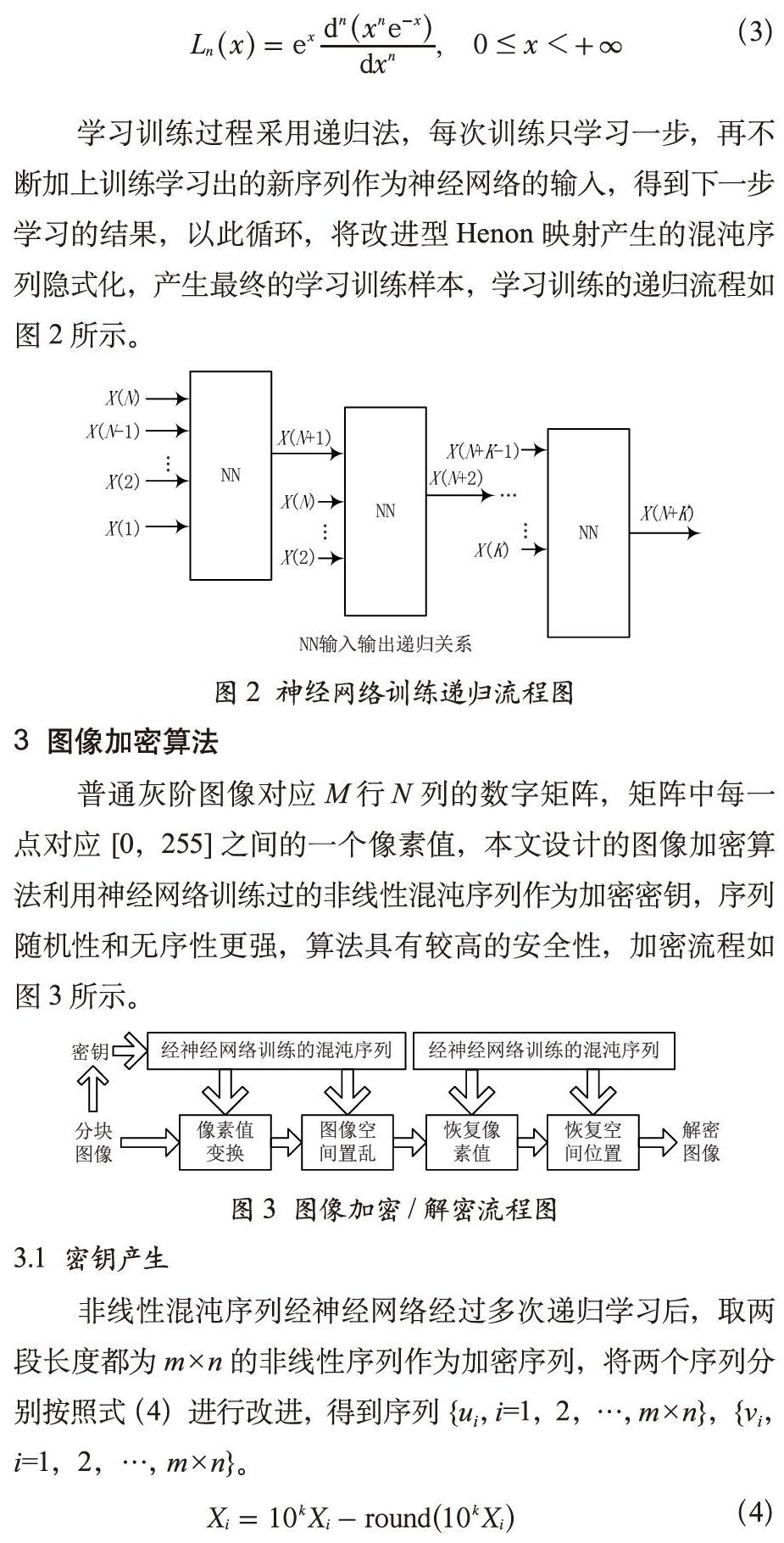
学习训练过程采用递归法,每次训练只学习一步,再不断加上训练学习出的新序列作为神经网络的输入,得到下一步学习的结果,以此循环,将改进型Henon映射产生的混沌序列隐式化,产生最终的学习训练样本,学习训练的递归流程如图2所示。
3 图像加密算法
普通灰阶图像对应M行N列的数字矩阵,矩阵中每一点对应 [0,255]之间的一个像素值,本文设计的图像加密算法利用神经网络训练过的非线性混沌序列作为加密密钥,序列随机性和无序性更强,算法具有较高的安全性,加密流程如图3所示。
3.1 密钥产生
非线性混沌序列经神经网络经过多次递归学习后,取两段长度都为m×n的非线性序列作为加密序列,将两个序列分别按照式(4)进行改进,得到序列{ui,i=1,2,…,m×n},{vi,i=1,2,…,m×n}。
3.2 图像处理
输入要加密的图像,得到图像的大小为M×N,边界用0填充,将图像处理为m×n。
3.3 图像像素变换
把待处理图像按照2×2进行分块,如图4所示,以块单位的方式对图像进行像素值变换。利用加密序列ui和vi构造图像像素变换矩阵。分别将ui和vi序列平均分为2组,然后将这4组序列转换成4个变换矩阵,记为A1,A2,A3,A4。采用按位异或的方式,分别用A1,A2变换1号、2号两个分块,用A3,A4变换3号,4号两个分块,将变换后的图像标记为K1,K2,K3,K4。
3.4 图像空间置乱
将序列ui和vi等分为4份,利用ui构造4个行置乱矩阵,记为M1,M2,M3和M4;利用vi构造4个列置乱矩阵,记为N1,N2,N3和N4。对应图像像素变换后的四个分块K1,K2,K3,K4按式(5)进行图像空间置乱,可得二次加密后的图像。
解密方法为上述过程的逆过程。
4 实验结果
本次试验采用BP神经网络训练改进型Henon混沌序列,实验参数设置:BP神经网络输入层含1个神经元,隐含层含5个神经元,输出层含1个神经元,输入层到隐含层神经元权值设置为1,隐含层到输出层权值设置为wi=0.5,神经网络中阈值设置为0。改进型Henon方程中x,y的初值分别取0.1和0.2,对标准图像Lena图像进行加密与解密。图像加解密结果如图5所示。
5 安全性分析
为了验证此算法的有效性和可行性,从以下几个角度对加密后的图像进行了分析。
5.1 统计学角度分析
从Lena图像直方图角度进行了分析,原始图像和加密图像的直方图比较如图6所示。曲线①代表原始图像的直方图,曲线②代表加密后图像的直方图,从直方图中可以看出加密信息在0~255内分布均匀,包含了原始图像的特征并展示了良好的效果。加密图像的直方图明显与原始图像不同,加密图像的直方图具有更高的安全性。
5.2 密钥空间角度分析
只有密钥空间能够承受住强力攻击,加密系统的良好性能才能得到保证。将两个密钥值之间的数学差设为10-10,对密钥进行微小改动,测试该加密系统对混沌初值的敏感性效果,测试结果如图7所示。由图7可知,当密钥有微小变化时,加密后的图像解密无法成功,因此可得出该加密系统对密钥的微小改变比较敏感,良好性达到要求的效果。
5.3 图像相关性角度分析
从水平、铅直和对角线三个方向,隨机选取了2 000个像素点,对原始图像与加密图像的相邻像素相关性进行分析计算,得到表1所列的相关系数。
由具体数字可知,加密后图像的相关系数远远小于原始图像,难以破译。
6 结 语
本文首先用改进型Henon映射产生的混沌序列,在BP神经网络中进行训练,得到基于混沌神经网络的非线性序列。经神经网络隐式混沌映射关系后,直接获取映射关系将变得十分困难。然后利用该隐式的非线性序列,结合图像加密算法,对图像进行加密和解密。最后从统计学、密钥空间和图像相关性角度对该算法进行了安全性分析,验证可知该算法加解密效果好,密钥敏感性强,抗统计分析能力强。未来工作的重心将放在对多维混沌系统进行神经网络训练上,同时优化加解密算法,进一步提高算法的效果和效率,以及提升系统的抗干扰能力。
参考文献
[1]ZHANG Y Q, WANG X Y. A symmetric image encryption algorithm based on mixed linear–nonlinear coupled map lattice[J].Information sciences,2014, 273(8):329-351.
[2]郑凡,田小建,范文华,等.基于Henon映射的数字图像加密[J].北京邮电大学学报,2008,31(1):66-70.
[3] MASSIMO C, FABIO C, ANGELO V. Chaos from simple models to complex systems[J]. Geier, 2009,15(3):916-923.
[4]刘家胜.基于混沌的图像加密技术研究[D].合肥:安徽大学,2007.
[5]孙亚军,王思明.并行人工神经网络通信开销的研究[J].计算机研究与发展,2000,37(2):155-158.
[6]李锦青,柏逢明,底晓强.基于Hopfield混沌神经网络的彩色图像加密算法研究[J].长春理工大学学报(自然科学版),2012,35(4):117-121.
[7]任晓霞,廖晓峰,熊永红.基于细胞神经网络超混沌特性的图像加密新算法[J].计算机应用,2011,31(6):1528-1530,1535.
[8]蒋诗意,王光义,靳培培.基于改进型Henon映射的图像加密算法[J].杭州电子科技大学学报(自然科学版),2017,37(5):1-6.
[9]王雅娟.基于混沌神经网络的图像加密算法[D].泉州:华侨大学,2013.

