UML活动图的正确性检测

陈慧峰　余晓菲　蒋建民

摘 要：UML（统一建模语言）活动图广泛用于软件开发过程，然而它是半形式化的模型，不能进行推理，无法保证其正确性。为了保证它的正确性，必须先把它转化为形式化模型再进行检测。现有工作已将活动图转换成变迁系统、进程代数、Petri网等模型，需要增加或丢失大量信息。本文提出一种新的方法，该方法直接将活动图转换成被称为依赖结构的形式化模型，不会增加或减少活动图的任何信息。基于依赖结构模型我们首先讨论了检测活动图的正确性方法，然后介绍相应的工具；最后用一个实例来详细说明检测过程。该工作有助于软件工程师正确地使用UML活动图对软件系统进行分析和设计。

关键词：活动图；形式化模型；正确性

中图分类号：TP311.5 文献标识码：A

Abstract：UML activity diagrams are widely used in the software development process.But since they are semi-formal models，we can neither reason nor guarantee their correctness.In order to ensure their correctness，they must be transformed into formal models and then can be detected.Existing work has transformed activity diagrams into formal models such as transition systems，process algebras and Petri nets.However，these models need to add or decrease a large amount of information.In this paper，a new method is proposed，which directly transforms activity diagrams into formal models called dependency structures without adding or decreasing any information.Based on the dependency structure models，we first present a method of checking the correctness of a UML activity diagram and then introduce a corresponding tool.Finally，an example was used to demonstrate the checking process in detail.This work is helpful for software engineers to properly use UML activity diagram to analyze and design software systems.

Keywords：activity diagram；formal models；correctness

1 引言（Introduction）

统一建模语言（UML）[1]是国际对象管理组织（OMG）认可的面向对象软件的标准化建模语言。它具有简单、统一的特点，而且能表达软件设计中的动态和静态信息，目前已成为软件开发可视化领域建模语言的工业标准。在软件系统的开发过程中，UML可以在软件开发整个生命周期中使用。实践证明，正确地使用UML可以帮助设计者缩短设计时间，减少开发成本。

UML活动图作为统一建模语言最重要的组成部分之一，它广泛用于软件系统的开发过程，它贯穿于需求分析到系统建成后测试的各个阶段。当前，在软件开发过程中许多工程师不能规范使用活动图，这导致无法正确地进行需求分析和设计，以致于整个软件开发项目失败，浪费了大量的时间和金钱。因此需要规范、正确地使用UML活动图。

本文给出了UML活动图形式化定义，由此可以确定给定的UML活动图的规范性，并将活动图转换为称为“依赖结构”的形式化模型，基于形式化模型可以检测该活动图的正确性。在本文中，我们开发了一个原型工具，并用一个实例详细演示了检测活动图规范化和正确性的过程。

UML活动图形式化的定义一直以来是一个热点问题，林添荣等[2]基于Hoare逻辑给出了UML活动图形式化定义，并根据此定义得出若干性质。Trickvoic等[3]用Petri网作为UML活动图形式化语义并给出了UML活动图转换为Petri网的规则。王聪等[4]给出的UML活动图操作语义是基于状态变迁，处理起来相对复杂。朱雪阳等[5]根据UML活动图定义了一种称为XYZ活动图的中间结构，然后将XYZ映射为XYZ/E条件元。崔萌等[6]在UML活动图的基础上加入了时间概念，然后定义了一种“实时”活动图。

由于UML活动图是半形式化的模型，我们不能直接推理和完成自动分解。这就需要我们选择合适的形式体系的活动图的语义模型。主流形式体系大致分为变迁系统[7，8]，进程代数[9-12]和Petri网[13]等。变迁系统是一个基于自动机的模型，包括狀态和转换。这些变迁可以是活动，动作或事件。当一个UML活动图被翻译成一种变迁系统[14，15]，因为在活动图中不存在状态信息，我们需要增建状态信息。同样地，如果一个活动图被转换成一个Petri网，在这样的Petri网的地方也需要被附加地建立[16，17]。进程代数是一个动作/根据活动积分。如果一个活动图映射到一个过程中，我们必须添加表达活动图[18，19]的同步控制同步事件名称。此外，现有的一些努力，例如Daw[20]提出了活动图的操作语义。这样的语义实际上是一种基于变迁系统的结构操作语义。

我们采用依赖结构作为形式化模型[21-23]，该模型是本文作者及团队成员耗费近10年研究基于事件的形式化模型而开发出的新模型。该模型考虑到了简单、实用、轻量级，并参阅Petri网有的令牌机制，进程代数的组合运算操作。更重要的是活动图直接可以转换成依赖结构，无需增加或减少任何信息。

2 活动图形式化定义（Formal definition of activity diagram）

活动图是用来描述系统的动作行为，我们能够定义一个活动图的抽象语法。在这里，以表示A集合的基，定义为在A上的一个二元关系。下面我们给出活动图的定义

定义2.1：一个活动图是一个四元组，其中：

（1），这里，AN是活动节点的集合，ON是对象节点的集合，，Ch是分支节点的集合，Me是合并节点的集合，Fo是分叉节点的集合，Jo是汇合节点的集合；

（2）是节点间的关系；

（3）Ia是初始节点的集合；

（4）Fa是终止节点的集合。

为了正确使用活动图，必须对活动图进行规范化处理。在UML活动图的规范[1]中，一个初始节点没有输入并只有一个输出，活动节点有一个输入和一个输出，分叉（Fork）有一个输入和多个输出，汇合（Join）有多个输入和一个输出，分支（Choice/Decision）有一个输入和两个或多个输出，合并（Merge）有多个输入和一个输出，终止节点有一个输入没有输出。表1提供UML活动图各类节点的入度和出度具体要求。

上面给出了活动图的形式化定义，基于定义2.1，我们可以定义节点的出度和入度。

定义2.2：设是一个活动图，设，，。和分别称为的入度和出度。

有了一般活动图和它的节点的入、出度定义，我们就可以定义“规范的活动图”。

定义2.3：设是一个活动图，如果对任意满足如下条件：

（1）若是活动节点或对象节点，则并且；

（2）若是初始节点，则并且；

（3）若是终止节点，则并且；

（4）若是分叉节点，则并且，是有限正整数；

（5）若是汇合节点，则并且，是有限正整数；

（6）若是分支节点，则并且，是有限正整数；

（7）若是合并节点，则并且，是有限正整数。

我们称G是一个规范的活动图。

命题2.1一个规范的活动图是一个活动图。

证明：根据定义2.1和定义2.2直接可得。

实际上，一个规范的活动图是一个特殊的活动图，它满足一些规范化的条件。

从定义2.1可以看出，活动图实际上是一个有向图，可以直接通过图的遍历算法，获取每个节点的入度和出度，当遍历整个活动图时，可以判断活动图节点的出度和入度是否满足定义2.3。如果每个节点的入度和出度满足定义2.3，则活动图是规范的；否则，该活动图是不规范的。

上述方法是从语法角度来判断活动图的规范性，但更重要的是检测活动图的正确性，即判断是否死锁，下面部分我们将讨论将活动图转换成形式化模型，并对活动图进行正确性检测。注意，我们可以将任何活动图（不一定是规范的活动图）转换成形式化模型，并检测它的正确性。

3 形式化模型（Formal models）

依赖结构形式化模型包含四部分：转换关系、同步关系、选择（排斥或冲突）关系和优先级关系。下面我们介绍该模型。

3.1 依赖结构

为了方便叙述，本文首先给出一些辅助性的记法。假定E是事件的集合，表示集合E的幂集，而且令。一个“事件集”是指事件的集合，如果一个事件集中的所有事件都已经出现，则称该事件集是“可用的”，否则称它是“不可用的”。

定义3.1：依赖结构是一个七元组，其中：

（1）是非空的、有限的事件集合；

（2）是初始可用的事件节点的集合；

（3）是转换关系；

（4）是同步关系，并且满足：；

（5）是选择关系，并且满足：；

（6）是优先级关系；

（7）是最后可用的事件集的集合。

一个转换依赖（A，B）就是集合B中所有事件都依賴于集合A中所有的事件。一个集合时称同步集；一个集合 时称选择集。任何一个同步集或者选择集中至少有2个事件，同步关系不采用二元关系，目的是区分一个共享的同步的事件。例如，一个事件e分别和同步，但我们可以要求和这两个事件不相互同步，也就是说同步关系不具传递性。因此，同步关系没定义成在事件集上的对称并传递的二元关系。选择关系也需要去考虑类似情况。任意集合表示所有A集合中的事件都相互同步。只有当A集合中所有的事件出现时，依赖于A中的所有事件才可能出现。任意集合表示B集合中的所有事件都相互排斥，也就是说，B集合中一个事件出现，则B集合中其他事件都不能出现。

优先级依赖控制并发事件，也就是说这些事件相互独立。初始可用的事件集即系统开始运行之前可用的事件集。终止事件集是指在系统执行过程中该事件集可用后，该系统或它的子系统就停止运行的事件集。

这里，对于任意的集合，若则称是一个转换依赖，表示为，读作“B依赖A”，并且A，B分为称转换依赖的前置事件集和后置事件集。对于任意的集合，若则称是一个优先级依赖，表示为。

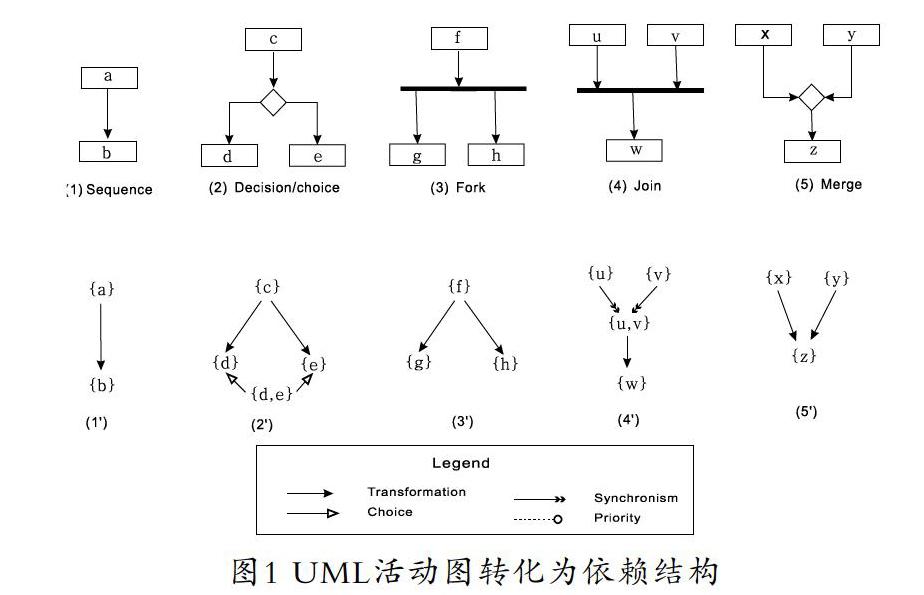
一个依赖结构能图形化表示。如图1所示，图中一个事件集表示成一个集合，一个转换依赖表示为从一个事件集指向另一个事件集的一个箭头，优先级依赖表示为终点带圆圈的虚线。为了图形化表示类似转换依赖关系的同步关系，每一个同步的事件形成的集合和同步关系表示为一个事件集指向它的同步事件集的双箭头。选择关系图形化表示为一个选择事件集指向可执行的单个事件集的空心箭头。

3.2 执行语义

依赖结构的执行语义模拟了所建模系统的执行过程。正如前文所述，在依赖结构中的每一个转换依赖（不包含优先级依赖）对应于一个活动（操作或动作），也就是一个执行步骤。若一个转换依赖的前置依赖集是可用的，则称该转换依赖是“已激活的”。只有已激活的转换依赖才可能被执行。为此，将计算过程中的当前可用的事件集，以及当前已激活的转换依赖作为一个整体，称为一个“状态”。

定义3.2：设是一个依赖结构，DS的一个状态是一个二元组，其中，是可用事件集的集合，是已激活的轉换依赖的集合并满足。DS的初始状态为，这里，和。

这里定义了状态，下面给出状态演化规则。

定义3.3：设是一个依赖结构，和是DS的两个状态。如果下列条件成立：

我们称能够通过执行转换依赖（A，B）演化成，表示为。

第一个条件要求当前可执行的转换依赖（A，B）是当前状态下已激活的转换依赖，第二个条件要求不存在一个事件比B中的事件优先出现，第三个条件要求新状态中已激活的转换依赖包含后继可激活的转换依赖，最后一个条件要求是：如果存在一个已激活的转换依赖它的前置依赖集是A，那么新状态下仍然保留事件集A，否则移除事件集A，新的可用的事件必须添加到新的状态中。

3.3 性质

为了把依赖结构用于分析系统的性质和行为。本节先定义一些依赖结构的性质。

定义3.4：设是一个依赖结构，并设是DS的初始状态。

（1）如果在DS中存在一个状态S，且存在一个状态序列，使得，其中，则称状态S在DS中是可达的。如果在DS中存在两个状态S和并且存在状态序列使得，其中，则称状态可达至状态S，表示为。Sta（DS）表示DS中所有可达状态的集合。

（2）设，如果并且，则称S是终止的；如果S不是终止的并不存在一个状态使得，则称S是死的。如果任意状态S是终止的或者存在一个终止状态，使得，则称DS是弱终止的。如果使得S是死的，则称DS是死锁。如果不存在使得S是死的，则称DS是无死锁的。

作者所在研究小组已经在文献[21-23]中对系统中死锁的存在与否进行了研究，并提出了一个可达性算法用于检测死锁。

命题3.1设是一个依赖结构。

（1）如果DS是弱终止，则称DS是无死锁的。

（2）如果并且，则称S是死的。

证明：由定义4.4直接可得。

上述命题表明（1）一个无死锁的系统比弱终止的系统是更一般的系统；（2）如果一个状态已激活的转换依赖集为空并且可用事件不都是终止事件，则该状态是死的。

4 转换规则（Transformation rules）

这里我们列出了活动图转换为依赖结构的具体规则，如图1所示。一个活动看成一个事件，一个活动节点看成一个事件集，下面给出六个转换规则。

（1） 一个活动节点与另一个活动节点通过一个带箭头的线（活动边）连在一起（如图1（1）所示），该带箭头的线对应着一个转换依赖，如图1（）所示。

（2）一个活动节点通过一个菱形分支到两个活动节点，如图1（2）所示，该菱形的分支结构对应着一个选择依赖，如图1（）所示。

（3）一个活动节点通过一条粗横线分叉成两个活动节点，如图1（3）所示，该粗横线的分叉结构对应着两个转换依赖，这两个转换依赖有相同的前置集，如图1（）所示。

（4）两个活动节点通过一条粗线汇合到一个活动节点，如图1（4）所示，该粗线的汇合结构对应着一个同步依赖，如图1（）所示。

（5）两个活动节点通过一个菱形合并成一个活动节点，如图1（5）所示，该菱形的合并结构的对应着两个有相同后置集的转换依赖，如图1（）所示。

（6）初始节点和终止节点只是起一个控制作用，在这里当作特殊点不用进行转换，但初始节点的后置节点转换为依赖结构图中的初始节点，终止节点的前置节点转换为依赖结构图中的终止节点。

命题 4.1设是一个规范的活动图，并假定通过上述转换规则得到依赖结构，则下面结论成立。

（1）若a在G中是活动节点或对象节点，则；

（2）若a在G中是初始节点并且，则；

（3）若b在G中是终止节点并且，则；

（4）若a在G中是分叉节点，则；

（5）若a在G中是汇合节点，则存在一个同步集；

（6）若a在G中是分支节点，则存在一个同步集；

（7）若a在G中是合并节点，则。

证明：（1）因为一个活动看成一个事件，一个活动节点看成一个事件集，所以（1）正确。（2）由转换规则（6）可得，初始节点并没有进行转换，但它的后继节点对应着依赖结构图中的初始节点，因此该结论正确。（3）由转换规则（6）可得，终止节点并没有进行转换，但它的前置节点对应着依赖结构图中的终止节点，因此（3）正确。（4）通过转换规则（3）可得，若a在G中是分叉节点，它只是起控制作用，并不属于 ，因此（4）正确。（5）通过转换规则（4）可得，若a在G中是汇合节点，正好对应着一个同步依赖，因此（5）正确。（6）通过转换规则（2）可得，若a在G中是分支节点，正好对应着一个选择依赖，因此该结论正确。（7）通过转换规则（5）可得，若a在G中是合并节点，它起的是控制两个或多个活动合并，则它不是一个活动。

5 工具及实例研究（Tool and case study）

我们的工具DS Tool是在开源图形软件JFDraw的基础上建立起来的，JFDraw是基于Java开发的矢量图形软件，拥有标准的矢量图形（矩形、直线、圆、弧、曲线），支持多种文件格式 （XML、JPG、PNG）。DS Tool将JFDraw的绘图功能修改成可以直接画UML活动图和依赖结构图，并以XML文件保存节点和图形信息。通过第4节的转换规则，可以将UML活动图转换成依赖结构模型，然后通过依赖结构的可达性算法，判断依赖结构是否存在死锁，从而确定活动图的正确性。

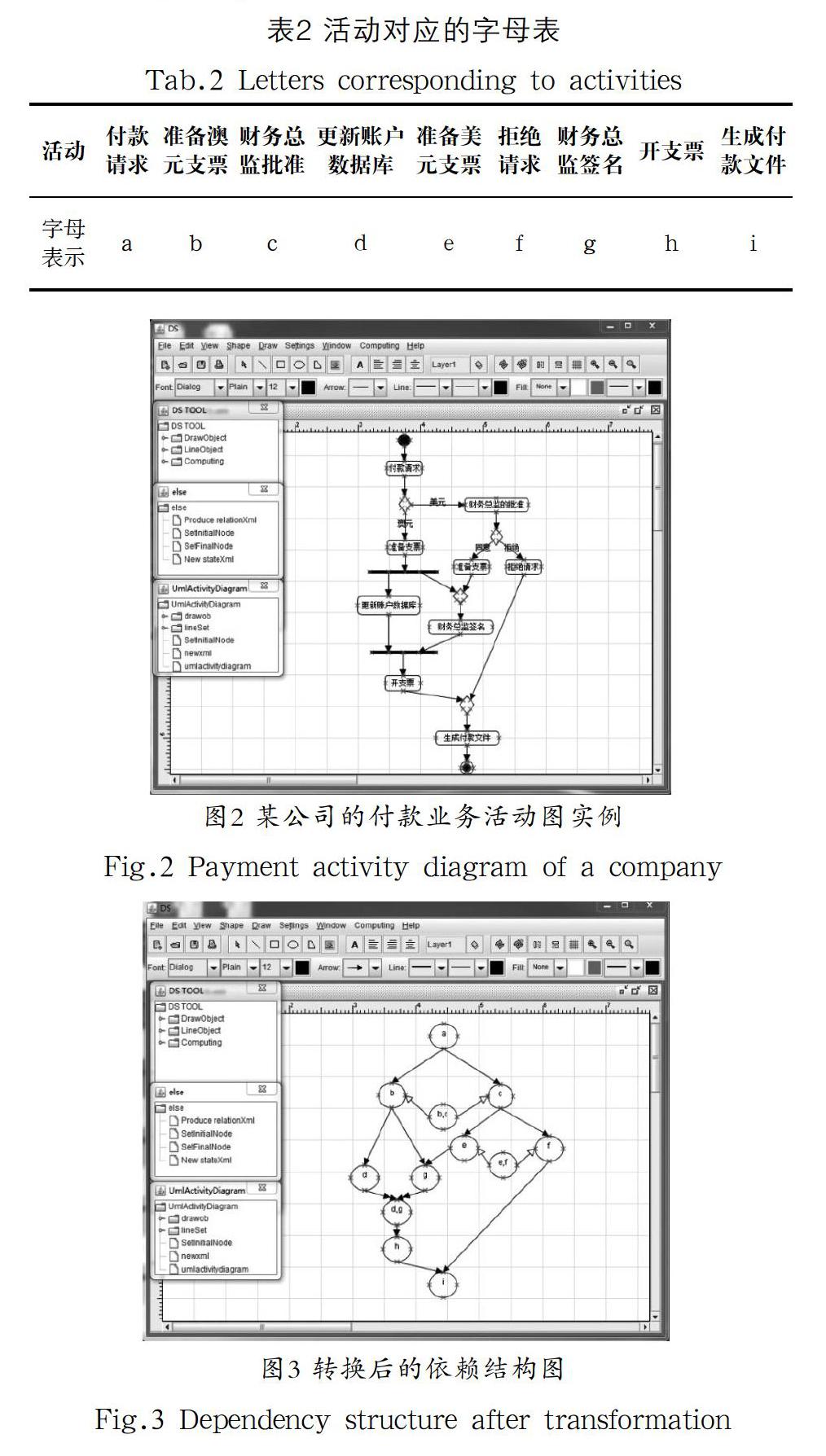
这里讨论一个实际应用的例子，通过该实例来演示如何使用我们的工具来判断活动图的正确性。图2是某公司的付款业务的活动图实例，从付款请求开始，可选择美元或者澳元。若选择美元，则需要财务总监批准，当财务总监批准，则准备支票并由财务总监签名，否则拒绝请求。若选择澳元，就直接准备支票，然后财务总监签名并更新账户数据库，最后开支票。无论哪种付款方式都将生成付款文件。

为了简化问题，将图2的活动图的活动用字母代替，在表2中给出了所有活动对应的字母。通过表2转换后得到图3所示的依赖结构图。利用我们工具中对依赖结构的可达性算法可以计算出在d和g同步过程出现死锁，即财务总监签名后，并没有更新账户数据库，如图4所示。

我们的工具对实例的活动图处理后生成13种状态，发现在第9个状态即 执行完后出现死锁。

6 结论（Conclusion）

本文首先给出了UML活动图形式化的定义，在此基础上再用算法对UML活动图进行正确性检测，然后将UML活动图转换为形式化模型依赖结构，并给出了依赖结构的执行语义、相关性质和活动图转换为依赖结构的规则，基于依赖结构检测UML活动图的正确性，最后通过我们的工具演示某公司的付款业务的活动图实例来判断活动图的正确性。该工具有助于工程师和软件开发初学者正确画UML活动图，在将来的工作中我们将进一步完善该工具，使其成为真正的CASE工具。

参考文献（References）

[1] Object Management Group.Unified Modeling Language Specification v2.2[EB/OL].http：//www.omg.org/spec/UML/2.2，2009-02-01.

[2] 林添荣，蒋建民.活动图的一种逻辑语义[J].福建师范大学学报，2010，26（3）：26-30.

[3] Trickvoic I.Formalizing activity diagram of UML by Petri nets[J].Journal of Mathematics，2000：30.

[4] 朱雪阳，唐稚松.UML活动图的时序逻辑语义[J].计算机研究与发展，2005，42（9）：1478- 1484.

[5] 王聪，王智学.UML活动图的操作语义[J].计算机研究与发展，2007，44（10）：1801-1807.

[6] 崔萌，李宣东.UML实时活动图的形式化分析[J].计算机学报，2004，27（3）：339-346.

[7] O.Marchal，P.Poizat， J.C.Royer.Checking Asynchronously Communicating Components Using Symbolic Transition Systems[J].CoopIS/DOA/ODBASE，2004（2）：1502-1519.

[8] M.Nielsen，G.Rozenberg，P.S.Thiagarajan，Elementary transition systems[J].Theoretical. Computer.Sci.，1992，96（1）：3-33.

[9] T. Bolognesi，E.Brinksma.Introduction to the ISO specification language LOTOS[J].Computer Networks and ISDN Systems，1987，14（1）：25-59.

[10] C.A.R.Hoare.Communicating Sequential Processes[J].Prentice-Hall，1978，21（8）：666-677.

[11] R.Milner，J.Parrow，D.Walker.A calculus of mobile processes[J].Information and Computation，1993，100：1-77.

[12] R.Milner.A Calculus of Communicating Systems[J].LNCS 92，Springer Verlag，1980，147：11-26.

[13] T.Murata.Petri Nets：properties，pnalysis，and applications[J].Proceedings of the IEEE，1989，77（4）：541-580.

[14] R.Eshuis，R.Wieringa.Tool support for verifying UML activity diagrams[J].IEEE Trans. Soft.Eng.，2004，30（7）：437-447.

[15] R.Eshuis.Symbolic model checking of UML activity diagrams[J].ACM Trans.on Soft.Eng. and Meth.，2006，15（1）：1-38.

[16] T.Staines.Intuitive mapping of uml 2 activity diagrams into fundamental modeling concept petri net diagrams and colored petri nets[J].ECBS，2008：191-200.

[17] H.St¨orrle.Structured nodes in uml 2.0 activities[J].Nordic Journal of Computing，2004，11（3）：279-302.

[18] I.Abdelhalim，S.Schneider，H.Treharne.An optimization approach for effective formalized UML model checking[J].SEFM，2012：248-262.

[19] J.K¨uster.A Classification of UML2 Activity Diagrams[J].Technical report，IBM ZRL Technical Report，2006：3673.

[20] Z.Daw，R.Cleavel.An extensible operational semantics for UML activity diagrams[J].SEFM，2015：360-368.

[21] Huifeng Chen，Jianmin Jiang，Zhong Hong，et al.Decomposition of UML activity diagrams[J].Software：Practice and Experience，2018，48（1）：105-122.

[22] Jian-Min Jiang，Huibiao Zhu，Qin Li，et al.Event-based mobility modeling and analysis[J].ACM Transactions on Cyber-Physical Systems，2017，1（2）：1-32.

[23] Jian-Min Jiang，Zhu，Huibiao，et al.Analyzing Event-Based Scheduling in Concurrent Reactive Systems[J].ACM Transactions on Embedded Computing Systems，2015，14（4）：1-27.

作者簡介：

陈慧峰（1992-），男，硕士生.研究领域：形式化方法.

余晓菲（1993-），女，硕士生.研究领域：形式化方法.

蒋建民（1972-），男，博士，教授.研究领域：形式化方法.