真空预压处理吹填土地基的数值模拟分析

卢俊言，孙树林，杨 扬，曾庆军

（1．中建市政工程有限公司，北京 100071；2．河海大学地球科学与工程学院，江苏 南京 211100；3．中交四航工程研究院有限公司，广东 广州 510230）

0 引言

真空预压法作为一种常用软土加固方法，具有工期短、加固效果好及节省工程费用等诸多优点，广泛应用于围海造地及港口建设等工程［1-4］。对真空预压吹填土地基处理工程的模拟与分析对于其加固效果和机理研究有重要意义。应舒等［5］针对因场区面积过大而导致的加固效果不明显的问题，提出二次插板，并通过数值模拟分析证明二次插板的加固效果更好；庄妍等［6］通过对某真空预压工程数值模拟，研究排水板参数与沉降量的关系，得出塑料排水板的打设深度对最终沉降影响最大；武亚军等［7］通过对软土地基采用不同加载方式进行数值模拟，并与实测数据进行对比，得出慢速加载方式较瞬间加载方式更有利于地基土加固。

1 工程简介

1.1 工程概况

广州南沙港区某真空预压加固吹填土地基工程试验区加固面积近2万m2，分区方式如图1所示。主要施工工艺为在吹填土表面铺设土工布和土工格栅，布置1m厚的中细砂垫层和0．6m厚的中粗砂垫层。试验区打设23m长的SPB-B型塑料，呈正方形分布，间距1m；水平排水管预埋在砂层表面下25cm处，各排水板间距不得大于6m。砂层上部铺有2层密封膜以保证各加固区的封闭性，各分区由砂袋组成的覆水围堰分开。设计加载方式为抽真空度至80kPa，使土体产生水压差，从而使土体内的自由水经塑料排水板排出地表而逐渐固结，逐步增加土体强度，改善其工程性质。

图1 试验区各分区分布

1.2 工程地质条件

该地基处理工程地处沿海软土地区，属第四系全新统海相沉积的饱和软土。工程场区自上而下分布如下：第①层为吹填土层，灰色，饱和，流塑～软塑状态，平均厚度3．1m；第②层为淤泥层（混砂），灰色，饱和，流塑～软塑，含粉、细砂、碎贝壳及腐殖质，平均厚度12．2m；第③层为淤泥质土，灰色，饱和，流塑～软塑，含泥质结核，平均层厚8．30m；第④层为黏土～粉质黏土灰黄色，浅灰色，棕红色，中等～硬，局部含铁质胶结物碎粒，平均层厚3．9m。

2 数值模拟

2.1 模型建立

在真空预压数值模拟中，需要将三维空间问题等效为平面应变问题。本文参照文献［8-9］，将砂井地基等效为砂墙地基。由于工程中的竖向排水体为塑料排水板，并非砂井，所以需将排水板尺寸转化砂井尺寸。HANSBO［10］提出塑料排水板转化砂井的等效直径为：

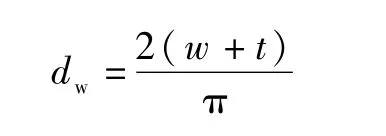
式中，w和t分别为塑料排水板横截面上的长宽，即其宽度和厚度。

本文模拟的是面积为55．5m×90．0m的试验分区1-1。根据对称性原则，模型加固区的宽度取试验分区短边的一半进行模拟与分析，即27．8m。影响区为从加固区边缘向外延伸50m，并用于研究真空预压对周围环境的影响。有限元模型的计算深度取30m，共分4个土层。有限元模型简图如图2所示，左边为加固区，右边为影响区，等效砂墙的深度与插水板打设深度一致，即23m。

吹填土地基采用修正剑桥模型模拟，各土层参数如表1所示。试验区里呈正方形布置的防淤堵SPB-B型塑料插水板间距为1m，深度为23m，截面面积为100mm×4mm，渗透系数为5×10-5m／s。

表1 有限元模型中的土层参数

试验区的整个加载过程分为3个阶段，分别为插板阶段、抽真空阶段和卸载阶段。由于吹填土地基中存在未消散的超静孔隙水压力，所以在插板期间，吹填土地基会产生一定量的沉降。因此在有限元分析中，应加上超静孔压而引起的沉降。抽真空阶段膜下真空度达到稳定为-80kPa。卸载阶段，射流泵工作停止，其表层真空负压降为0。

有限元计算网格划分如图3所示。相应的约束条件为：1面为全约束，即xy方向约束，无横向和竖向位移；2面为水平约束，即x方向约束，其中左2为轴对称约束，两者都只有竖向位移，无横向位移；3面和4面分别代表影响区和加固区的地表面，无约束，可自由变形，同时4面的加载方式由加载曲线确定。网格形状为四边形，网格单元类型为CPE4P，按照二次缩减积分法进行有限元计算。

图3 有限元模型网格划分及边界条件

2.2 模型验证

将实测成果与有限元计算模型结果进行对比，总结吹填土地基加固区中心的沉降规律及孔压变化情况，验证有限元模型的正确性。

2.2.1 地表沉降

根据真空预压有限元模型沉降云图可看出，模型的变化趋势与实测沉降变化趋势一致。根据边界条件和荷载情况，模型左边界即加固区中心的沉降量最大，而离加固区中心越远，地表沉降量越小，这与实测数据的变化规律是一致的。从沉降云图中还可看出，在真空预压加固区23m深度左右沉降较大，这说明真空预压的加固效果主要在插水板深度范围内。

从有限元模型单元节点竖向位移矢量图可看出，随着深度增加，土体沉降量越小，这符合真空度在插水板中传递存在井阻效应的规律。同时，在插水板打设深度以下的土体仍然存在较小沉降，这验证了真空预压的加固效果可达到插水板打设深度下数米。

图4为加固区中心的有限元模型沉降量和实测沉降量随时间变化曲线，模型计算结果与实测结果拟合效果较好，实测最终沉降量2．138m，模拟最终沉降量2．098m，总沉降误差为1．9%。插板期间实测沉降为0．4m，有限元分析中的插板期间沉降量为0．429m，这部分沉降为吹填土地基中的超静孔隙水压力随排水路径的缩短而消散引起的。真空预压期间，模型的沉降量先是较实测大，随着时间推移，实测沉降量超过模型沉降量，但两者沉降值基本符合，且两者的变化趋势一致，均为前期沉降量大、沉降速度快，后期沉降量小、沉降速度缓慢。真空卸载期间，有限元计算模型中土体发生了一定量的反弹，反弹量为0．043m。

图4 加固区中心地表沉降示意

2.2.2 孔隙水压力

从有限元计算模型的真空恒荷载期间土体孔隙水压力云图可看出，真空预压恒荷载期间，表层土体中的孔压变化最大，其大小略低于恒荷载时膜下真空度。随着深度增大，土体中孔压变化越来越小，这说明真空预压技术存在井阻效应，但在插水板打设深度以下，土体孔压仍有变化，这也说明真空预压加固的影响深度大于排水板的打设深度。从恒荷载期间的孔压云图中还可看出，模型右边的影响区的孔压也存在变化，离加固区越近，孔压变化越大。

将试验区1-1分区中心处不同深度土体中的孔隙水压力随时间变化的实测数据与有限元模型计算数据进行对比，选取深度分别为-3，-12，-21m，并分别绘制成曲线，如图5所示。可以看出，尽管计算值和实测值有一些差距，但有限元模型计算的孔压变化趋势和实测孔压变化趋势基本一致。其中，深度为-3m处土体的实测孔压最终变化量为-79 kPa，模型孔压变化量为-72 kPa；深度为-12m处土体的实测孔压最终变化量为-56kPa，模型孔压变化量为-61kPa；深度为-21m处土体的实测孔压最终变化量为-24kPa，模型孔压变化量为-31kPa。图中不同深度孔压的实测曲线在某个时刻存在回升，这是由停电、漏气及其他不可抗拒的自然原因引起，由于该类情况持续时间短，且加载总时间满足设计要求，并不会影响最终加固效果。随着深度增加，有限元计算出来的孔压变化值减小，这符合实测数据的变化规律。同时，在真空卸载后，有限元计算出来的各个深度的孔压持续增加到一个稳定值，符合工程实际情况。

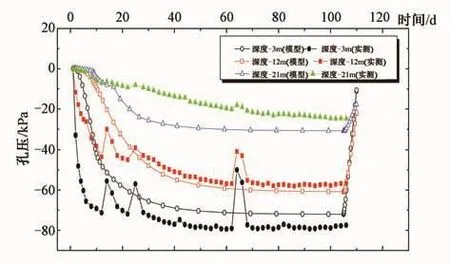
图5 加固区中心处不同深度孔压变化示意

通过对吹填土地基中心处沉降和孔压的有限元计算结果和现场实测结果对比分析可知，两者拟合度较高，这验证了数值模型的正确性。

3 固结度计算

固结度是判定加固效果的重要参数，工程上使用较多的是双曲线法和三点法判断地基后期沉降变化规律，即根据某时刻的沉降量演算该时刻的地基固结程度。

3.1 双曲线法推算固结度

双曲线法即选择实测沉降量和时间曲线，选定1个拐点to（通常选取恒荷载下的1个时刻），把实测St-t曲线的起点放在拐点处，由于沉降曲线近似双曲线。依据JTS 147-2—2009《真空预压加固软土地基技术规程》，得公式如下：

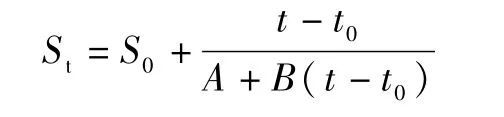
式中，S0为满载开始时的实测沉降量（cm）；St为满载t时刻的实测沉降量（cm）；t为满载预压时间（s），从满载时刻算起；S∞为最终沉降量（cm）；A、B为待定常数。

当时间t→∞，由式可得最终沉降量：

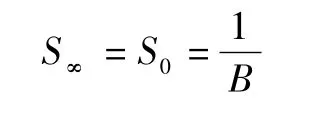
为求取待定常数A、B，将式改为：

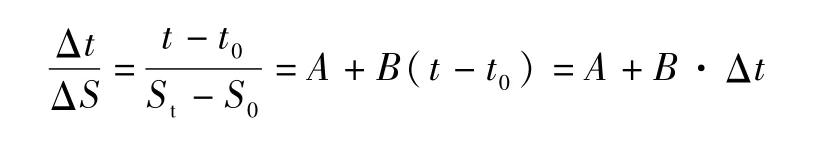
从上式可知，它是关系的直线方程。所以，只需算出某一时刻的B值即可得出该时刻的固结度。

如图6所示，以1-1分区中心沉降为例，分别以t＝0，10，20，30，40，50，61，71，81，90，96 d对应沉降量S＝731，999，1 191，1 323，1 437，1 533，1 603，1 663，1 710，1 731，1 738mm。S0＝731mm，抽真空前沉降量为400mm，B为0．000 8，可算出最终S∞＝2 381mm，实测最终总沉降量为2 138mm，最终固结度Uε＝St／S∞＝89．8%。

图6 双曲线模型预测最终沉降

3.2 三点法推算固结度

三点法又称对数曲线法，现简要对三点法计算的原理和计算过程进行分析。在实测前期的S-t曲线选择结束施加荷载后的3个时间点t1、t2和t3，并且t3尽量选择和曲线末端对应，时间差 （t2-t1）和（t3-t2）的值应控制的大一点且保证2个时间差相等。具体公式如下：

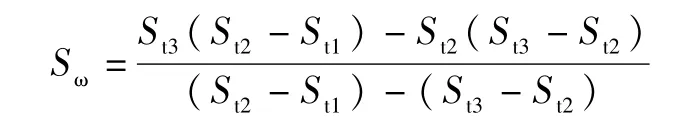
以1-1分区中心沉降为例，选定恒荷载期内的t1取10月6日，S1＝1 107mm，t2取11月15日，S2＝1 557mm，t3取12月25日，S3＝1 738mm，即可求出各沉降标位置土体最终沉降量，试验区1-1分区最终沉降量S∞＝1 860mm，实际沉降量为1 738mm，插板期间地基土的沉降量为400mm，所以最终固结度Uε＝St／S∞＝94．6%。

4 结语

1）在有限元模拟中，将吹填土中未消散的超静孔压等效为线性荷载施加在吹填土地基表面，以模拟插板期间的沉降。有限元计算得出插板期间沉降量为0．429m，实测插板期间沉降量0．400m，插拔期间沉降误差为7．3%。模拟最终沉降量2．098m，实测最终沉降量2．138m，总沉降误差1．9%。

2）真空恒荷载期间，加固区土体的沉降及孔压变化值与实测值有相同的变化趋势，影响区孔压也产生消散，并且消散值随着离加固区越近而变得越大。真空卸载后，模型计算出加固区中心表层土体发生微小反弹，反弹量约0．043m，可供同类工程参考。

3）双曲线和对数曲线法推算1-1分区固结度分别为89．8%和94．6%，说明真空预压加固吹填土地基的效果明显。

参考文献：

［1］TANG XW，ONITUKA K．Consolidation of ground with partially penetrated vertical drains［J］．Geotechnical engineering journal，1998，29（2）：209-231．

［2］LIU Y，XIAO S F，WANG Q．Research on indoor scale-sown test of dredger fill［J］．Rock and soilmechanics，2004（4）：519-528．

［3］许胜，王媛．真空预压法加固软土地基理论研究现状及展望［J］．岩土力学，2006，27（S2）：943-947．

［4］孙立强，闫澍旺，李伟．真空-堆载联合预压加固吹填土地基有限元分析法的研究［J］．岩土工程学报，2010，32（4）：592-599．

［5］应舒，陈平山．真空预压法中塑料排水板弯曲对固结的影响［J］．岩石力学与工程学报，2011，30（2）：3633-3640．

［6］庄妍，王晓东，崔晓艳．真空预压在有轨电车软土地基中的应用及数值模拟研究［J］．岩土工程学报，2016，38（1）：141-146．

［7］武亚军，覃萍，孙德安．不同加载方式下真空加固吹填软土的现场试验与数值模拟［J］．水运工程，2013（8）：165-172．

［8］赵维炳，陈永辉，龚友平．平面应变有限元分析中砂井的处理方法［J］．水利学报，1998（6）：53-57．

［9］陈小丹，赵维炳．考虑井阻和涂抹的砂井地基平面应变等效方法分析［J］．岩土力学，2005，26（4）：567-571．

［10］HANSBO S．Consolidation of clay by band-shaped prefabricated drains［J］．Ground engineering，1979，12（5）：6-18，21．