生物氧化预处理过程中氧化槽温度的预测控制∗

梁甜，高丙朋

(新疆大学电气工程学院，新疆乌鲁木齐830047)

0 引言

生物氧化预处理过程是用微生物对包裹金的矿物进行氧化，需要提取的矿物就会被解离或者以裸露状态混在氧化渣中，经过后续处理从中提取目的元素[1−2]．在实际生产过程中，由于受高寒地区高海拔、昼夜温差大等条件的影响，使得氧化槽内温度在不同季节、不同时间呈现出较大差异．因此，对氧化槽内温度进行控制实现快速性、稳定性是保证细菌活性及氧化还原进程的关键．

模型预测控制作为一种以预测模型、滚动优化和反馈校正为基础的过程控制优化算法[3]．在实际工业生产过程中，模型预测控制因其处理非线性能力得到广泛应用，并且取得了很多有意义的研究成果[4−7]．文献[8]对模型预测控制的发展现状做了简要综述并指出非线性预测控制对控制理论的进一步发展与应用的重要意义．文献[9]针对预测模型参数优化问题，提出了一种以多智能体参数寻优算法，设计了MAPSO支持向量回归模型．文献[10]设计了一种鲁棒预测控制器，用来解决一类非线性、不确定系统．文献[11]将TS模糊模型与基于粒子群优化的约束状态反馈预测控制相结合，用来解决具有严重非线性且带有系统约束的的控制问题．由于高寒地区外界环境对生物槽内部温度的严重影响，本文提出一种以在线最小二乘支持向量回归机（OLS-SVR）为模型的非线性预测控制方法．采用基于种群交流选择机制的自适应混沌粒子群算法滚动优化非线性模型预测控制的目标函数，求得最优控制量．仿真结果验证了该算法的有效性．仿真结果表明，所提算法能更好的保持氧化槽内温度达到稳之，保证氧化还原反应的高放进行．

1 预测模型

1.1 OLS-SVR建模原理

假设一个n维训练样本集为：{(xj,yj)|j=1,2,...,xj∈Rn,yj∈R}，式中，xj是输入样本，yj是输出样本．利用一非线性映射φ将样本映射到高维特征空间，设回归函数为：

式中，ω为权值矢量，b为偏差．

根据结构风险最小化原则，其优化问题如下：

式中，C为惩罚因子，ξi为松弛变量．

引入Lagrange乘子αi，式(2)的Lagrange函数为：

式中，αi≥0，i=1,2,...,N.

根据KKT条件消去ω，ξ可得如下函数：

其中，α=[α1···αN]T，Y=[y1···yN]T，Ω=φT(x)φ(xi)=K(x,xi)，K(x,xi)是满足Mercer的一个核条件函数，可得LS-SVR估计函数为：

本文选取径向基核函数为

为了实现在线建模，本文采用一种递推LS-SVR算法[12]．当增加训练样本时，可以利用上一次所得的参数通过递推得到新的参数，避免了求逆矩阵．算法如下：

令Φ=可得再令可得当新样本加入时有：

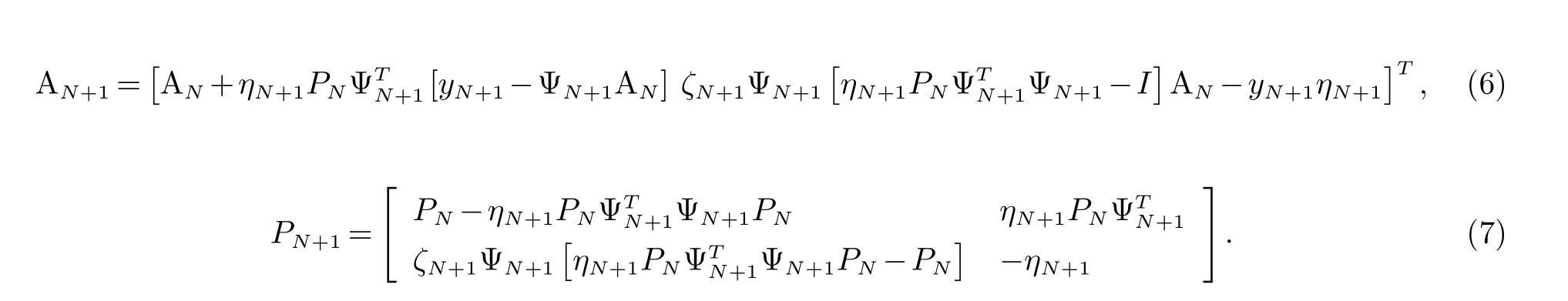
其中，

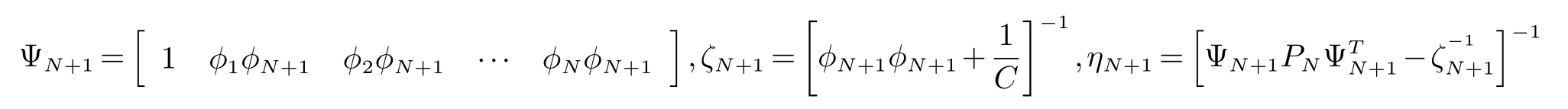
虽然递推LS-SVR算法可以避免求复杂矩阵的逆，但随着新数据的加入，模型参数维数也随之增大，内存需要也不断增加．所以要在建模过程中保持样本集大小不变，即一个新样本加入到样本集的同时删除一个旧样本．通过增加数据的递推LS-SVR算法的逆运算可得减少一个数据时的递推算法如下：

设当前样本集为：

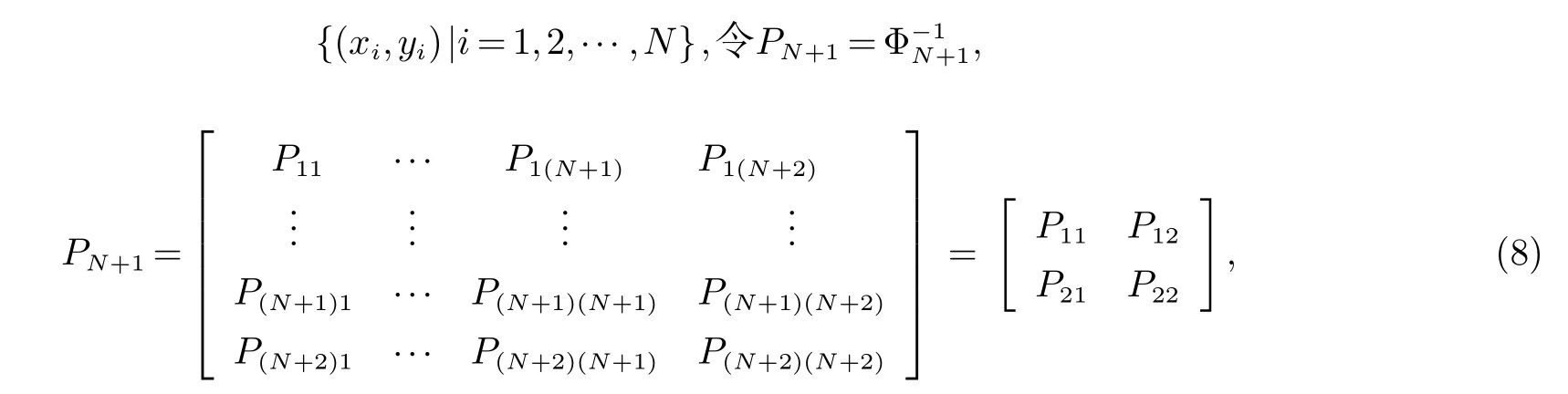
其中，

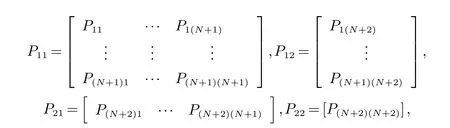
当要删除数据{xN+1,yN+1}时有：

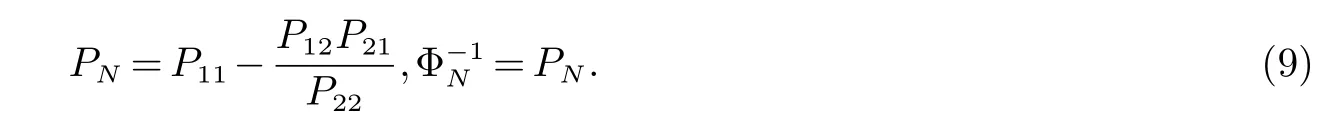
1.2 OLS-SVR预测模型

将被控对象的非线性系统描述为：

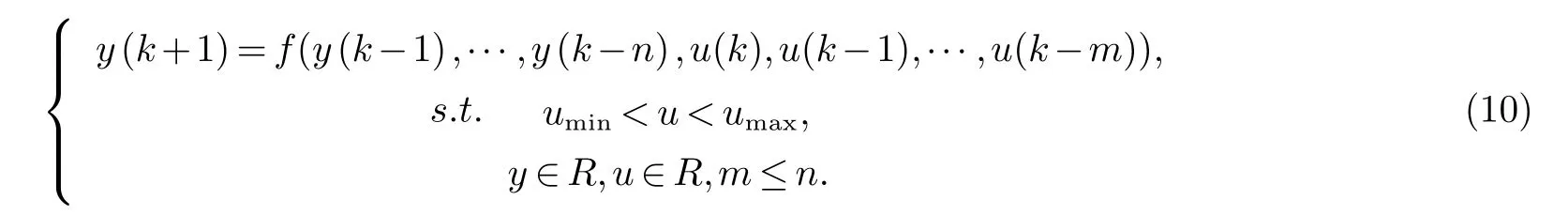
式中：f为生物氧化预处理过程氧化槽温度的OLS-SVR非线性模型，u和y分别表示输入、输出向量，m和n分别为其阶次．

将连续控制序列u(k−m),u(k−m+1),···,u(k)和相应输出y(k−n),y(k−n+1),···,y(k)作为OLS-SVR的输入输出．令

通过训练OLS-SVR得到非线性方程可得进一步OLS-SVR预测模型：

为了获得多步预测模型，移动式(12)中的时域，ym(k+j)为k时刻第j步预测输出，有：

2 滚动优化及反馈校正

本文对生物氧化预处理过程中氧化槽温度进行预测控制．对于式(10)所描述的非线性系统的目标函数为：

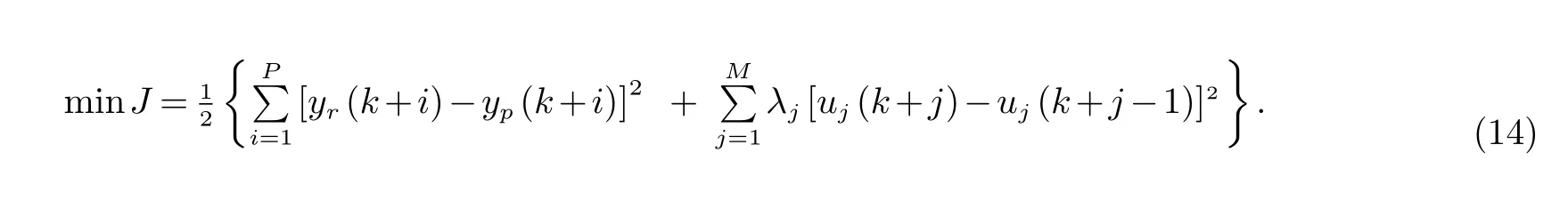
其中，P为预测时域，M为控制时域，λ为加权系数，u(k),u(k+1),···,u(k+j)为控制输入序列，yr(k+i)及yp(k+i)分别为i步参考输出和预测输出，有：

其中，h为补偿系数．

通过式(15)和(16)来建立反馈校正．

NMPC滚动优化的目的是寻找最优控制序列u(k),u(k+1),···,u(k+j)使得目标函数J最小，本文采用基于种群交流选择机制的自适应混沌粒子群优化算法实现对氧化槽温度在线求解的动态优化问题．

3 基于种群交流选择机制的自适应混沌粒子群优化算法

3.1 自适应混沌粒子群优化算法

在一个PSO系统中，多个候选解同时存在并相互作用，每一个解称为一个“粒子”，在解空间中飞行以寻求最佳的位置，每个粒子通过跟踪和记忆与相邻粒子在历史搜索中的最佳位置来调整自己，最终求得最优解．

搜索空间中的一个粒子状态具有两个特征：位置和速度，分别通过下面的式(17)和式(18)进行调整．

其中，Vi为粒子i的速度向量，Xi为粒子i的位置向量，pbest为粒子i前一时刻的最佳位置，gbest为种群中所有粒子的一个最佳位置，r1和r2为[0,1]之间的随机变量，C1、C2为加速常数，ω为惯性权重．

令ω根据粒子群的目标函数进行自适应变化，自适应惯性权重系数定义如下：

其中ωmax和ωmin分别代表ω的最大值和最小值，f为粒子当前的目标函数值favg和fmin分别为所有粒子的平均和最小目标函数值．

为了克服自适应粒子群算法局部搜索能力弱的缺点，引入混沌搜索来加强算法的局部搜索能力．混沌优化主要有两个重要步骤，首先将混沌空间映射到被优化问题的解空间，然后利用混沌遍历性、随机性等特征来实现对优化问题的求解．

采用Logistic来构建混沌动态：

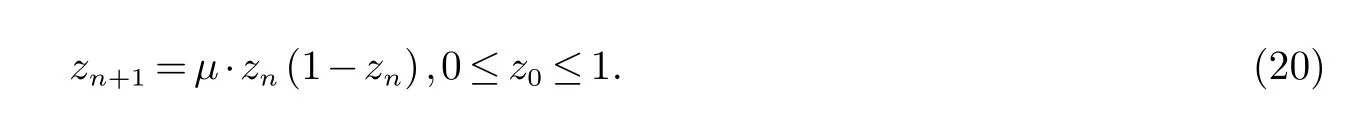
其中，µ为控制参数，x为变量n=0,1,2,···，当µ=4时，系统完全处于混沌状态．在算法早熟收敛时，位置更新如下式：

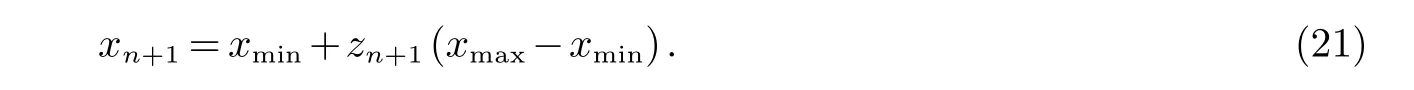
3.2 种群交流选择机制

为了更好地平衡算法的全局搜索和局部搜索能力，本文提出了一种基于种群交流选择机制的自适应混沌粒子群优化算法．即在APSO搜索完成后，通过种群交流选择机制选择具有较高适配度的粒子进行混沌局部搜索．此方法的优点在于：利用种群交流选择机制可以使具有较高适配度的粒子获得更多执行混沌搜索的机会．种群交流选择机制的实现步骤如下：

Step1:把群体分成A和B两部分，对A群体采用轮盘赌选择机制，对B群体采用锦标赛选择机制；

Step2:A内的少部分粒子进入B内，B群体拿出同等数目的粒子与之交叉．同理，B内的少部分粒子进入A内，A拿出同等数目的粒子与之交叉，以此形成两个新的子体；

Step3:其余部分个体按照各自群体的选择方式产生新的群体；

Step4:两个新的子体分别进去新的群体；

Step5:达到要求的迭代次数时停止，否则回到Step1．种群交流选择机制示意图，如图1所示．

3.3 基于种群交流选择机制的自适应混沌粒子群优化算法步骤

Step1:参数初始化．随机初始化Xi及Vi；

Step2:以第i个粒子位置分别设置为该粒子的当前位置pbest和初始群体中最佳粒子位置gbest；

Step3:对每个粒子i，根据式(17)、(18)、(19)更新Xi及Vi．计算所有粒子的fi；

Step4:若粒子i适应度好于pbest的适应度，则粒子当前的Xi替换pbest，若粒子i适应度好于gbest的适应度，则粒子当前的Xi替换gbest；

Step5:计算所有粒子的fi．对每个粒子i，根据式(21)、(17)、(18)更新Xi及Vi；

Step6:对通过种群交流选择机制选择出来的具有较高适配度的粒子按式(20)、(21)执行混沌局部搜索；更新pbest及gbest；

Step7:若满足停止准则，输出当前最优解，否则令k=k+1返回Step3．

图1 种群交流选择机制

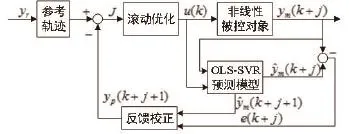
图2 非线性系统模型预测控制的结构框图

3.4 预测算法步骤

Step1:设定算法参数．对系统初始化；

Step2:用OLS-SVR对现场采集的输入输出样本进行训练，建立OLS-SVR预测模型；

Step3:通过比较系统实际输出和估计输出得到预测误差err(k)；

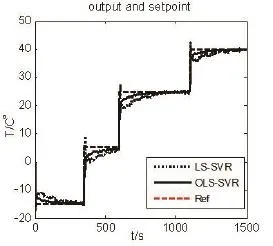
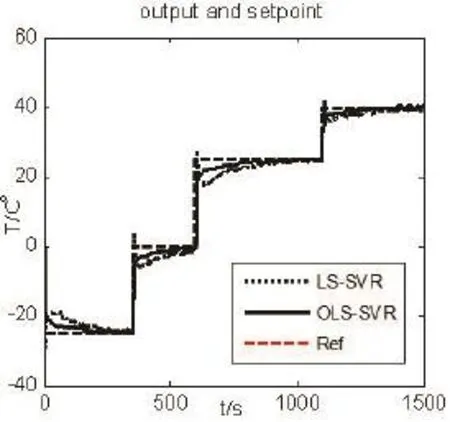
Step4:用测试样本对OLS-SVR模型进行测试，若err(k)

Step5:通过式(15)和(16)进行在线的反馈校正，得到系统的实际预测输出值yp(k+i)；

Step6:采用基于种群交流选择机制的ACPSO优化算法对NMPC进行在线滚动优化，若满足终止条件，输出最优控制序列，否则，执行Step7；

Step7:将控制量u(k)应用于系统，令k=k+1返回Step3．

通过上述分析，可得基于OLS-SVR非线性系统模型预测控制的结构框图，如图2所示．

4 仿真结果

以新疆某生物氧化-氰化提金厂作为对象进行相关研究，从已处理的数据中选取200组数据作为初始数据，150组数据中前100组数据作为训练样本，剩下数据作为测试样本．在生物氧化预处理过程中分别用LS-SVR和ROLS-SVR模型建立温度预测模型．选取矿浆浓度、进气量作为模型输入，温度作为模型输出，使用测试样本对两种模型进行测试，预测结果如表1所示．

我们选取了不同时刻的温度进行预测控制．控制时域为2，预测时域为2，λ=0.01，误差精度ε=0.000 01，粒子群个数为20，最大迭代数为100，采样时间为15min，得到仿真结果如图3、4、5、6所示．由仿真结果可见，外界温度对系统影响较大，随着室外温度的升高，氧化槽内温度的控制效果会更好，在不同起始温度下，OLS-SVR系统的响应速度快，调解时间短，能更稳定的达到设定值．

表1 OLS-SVR和LS-SVR的预测结果比较

图3 起始温度T=-25◦C

图4 起始温度T=-15◦C

图5 起始温度T=5◦C

图6 起始温度T=25◦C

5 结论

由于高寒地区昼夜温差大，极端天气出现频繁，对生物氧化预处理过程中氧化槽温度有极大影响，本文提出一种以OLS-SVR的非线性模型预测控制算法．采用基于种群交流选择机制的自适应混沌粒子群算法对非线性模型预测控制的目标函数滚动优化，求得最优控制量．通过与基本LS-SVR算法进行比较，仿真结果表明，在不同外界温度下，本文算法仍然响应速度快、调节时间短、超调小，能更好的使氧化槽温度达到稳定，保证氧化还原反应的高效进行．

参考文献：

[1]Li Q,Li D,Qian F.Pre-oxidation of high-sulfur and high-arsenic refractory gold concentrate by ozone and ferric ions in acidic media[J].Hydrometallurgy,2009,97(1–2):61-66.

[2]杨玮.复杂难处理金精矿提取及综合回收的基础研究与应用[D].长沙:中南大学,2011.

[3]Qin S J,Badgwell T A.A survey of industrial model predictive control technology[J].Control Engineering Practice,2003,11(7):733-764.

[4]Rodriguez J,Kazmierkowski M P,Espinoza J R,et al.State of the Art of Finite Control Set Model Predictive Control in Power Electronics[J].IEEE Transactions on Industrial Informatics,2013,9(2):1003-1016.

[5]Salsbury T,Mhaskar P,Qin S J.Predictive control methods to improve energy efficiency and reduce demand in buildings[J].Computers&Chemical Engineering,2013,51(14):77-85.

[6]Wang T,Gao H,Qiu J.A Combined Adaptive Neural Network and Nonlinear Model Predictive Control for Multirate Networked Industrial Process Control[J].IEEE Transactions on Neural Networks&Learning Systems,2016,27(2):416-425.

[7]Heidarinejad M,Liu J,Christof i des P D.Economic model predictive control of nonlinear process systems using Lyapunov techniques[J].Aiche Journal,2012,58(3):855–870.

[8]席裕庚,李德伟,林姝.模型预测控制—现状与挑战[J].自动化学报,2013,39(3):222-236.

[9]唐贤伦,李洋,李鹏等.多智能体粒子群优化的SVR模型预测控制[J].控制与决策,2014(4):593-598.

[10]苏成利,赵家程,李平一类具有非线性扰动的多重时滞不确定系统鲁棒预测控制[J].Acta Automatica Sinica,2013,39(5):644-649.

[11]王书斌,单胜男,罗雄麟.基于T-S模糊模型与粒子群优化的非线性预测控制[J].化工学报,2012,63(s1):176-187.

[12]李丽娟.最小二乘支持向量机建模及预测控制算法研究[D].杭州:浙江大学,2008.