基于改进DCNN结合迁移学习的图像分类方法∗
杨东旭,赖惠成,班俊硕,王俊南
(新疆大学信息与工程学院,新疆乌鲁木齐830046)
0 引言
近年来,深度卷积神经网络在计算机视觉领域的很多任务中取得了十分显著的成功,如目标检测[1,2]人脸识别[3,4],大规模图像分类[5]等.国内外研究学者针对DCNN模型做了很多研究.例如Shankar[6]等人对网络模型结构的研究,Goodfellow等人[7]对非线性激活函数的研究,Raymond等人[8]对池化层采用不同池化方法的研究.而采用SGD(Stochastic Gradient Descent)结合BP(Back Propagation)的方法进行训练与使用Softmax做分类已经成为DCNN模型的默认组成部分.在依靠SGD结合BP的方法优化模型时,标准SGD通过链式法则来计算和传播梯度,尤其是训练深层网络模型时,使用连续而完整的梯度进行传播对网络模型的表现起到了十分关键的作用,因此神经元或网络层出现的饱和问题会影响梯度信息的完整性.He等人[9]使用ReLU和PReLU代替sigmoid激活函数解决由sigmoid饱和导致的梯度消散问题.为去除神经元饱和,Krizhevsky等人[10]提出采用非线性分段函数代替sigmoid函数.为去除网络层饱和,Huang等人[11]提出了密集连接网络,使梯度信息可以在没有梯度消散的情况下从一层传播到任意层.研究发现只有过早的饱和是我们不需要的,而不是所有饱和情况.因此,本文采用注入噪声的方法来延迟早期饱和.Nair等人[12]的研究是将噪声加入到ReLU中使前馈网络产生更完整的梯度信息,Gulcehre等人[13]将噪声加入到sigmoid激活函数中,加入自适应权重噪声[14]和梯度噪声[15]等方法都可以有效提高模型性能.
Softmax函数与sigmoid函数公式结构十分相似,也同样存在饱和问题.研究者更多关注对DCNN模型特征提取能力的改进,而处在模型最后面的Softmax分类层往往被研究者忽略.在进行标准的SGD过程中,当接收到一个较大的输入时,Softmax存在的过早饱和问题会使梯度过早消失,导致BP只能反向传播不够完整的梯度,从而使模型无法进行更充分的参数更新.随着训练的继续,输入样本对梯度传播的贡献逐渐降低,参数难以更新网络优化停止.这也是模型陷于局部最小的原因之一,同时提高了过拟合出现的几率.受前人研究启发,本文通过注入噪声的方法来改进Softmax分类性能.首先,对Softmax函数的过早饱和问题做深入探究,然后提出一种延迟Softmax过早饱和的方法.在Softmax函数中注入噪声产生更为连续而完整的梯度用于反向传播,从而有效延迟过早饱和,使模型逃离局部最小,同时有效避免了过拟合以提高模型的泛化能力.最后,针对参数随机初始化训练困难、耗时长的问题,采用预训练模型参数来代替随机初始化参数,使模型可以在较短时间内达到较高的识别率.
1 基本概念
1.1 激活函数
在人工神经网络中,神经元上的激活函数定义了神经元输出的映射关系.Bengio教授在ICML2016的文章[13]中给出了激活函数的定义:激活函数是映射h:R→R,并且处处可微.激活函数在网络中的作用是提供非线性映射的能力,因此激活函数一般都是非线性函数,并且是训练深层网络不可或缺的部分.
1.1.1 软/硬饱和
对于激活函数h(x),当称为右侧软饱和;当称为左侧软饱和;若同时满足上述两种情况就统称此函数为软饱和激活函数,Sigmoid函数就是软饱和激活函数.与软饱和相对的是硬饱和激活函数,即:当|x|>c时h(x)=0,其中c为常数.如果同时满足右侧硬饱和与左侧硬饱和,就统称此激活函数为硬饱和激活函数.
1.1.2 梯度消失
对于Sigmoid激活函数来说,由于它的软饱和性,反向传播过程中的输入一旦落入饱和区域,梯度就会接近于0.这样的梯度贡献会导致网络参数很难得到有效训练,从而使网络的优化停止,这种现象被称为梯度消失.通常情况下,使用Sigmoid激活函数的网络在5层内就会出现梯度消失的现象.这正是过去很长一段时间里阻碍神经网络发展的重要原因之一.部分研究学者提出一些优化方法得到有效缓解,但梯度消失问题至今仍然存在.
1.2 迁移学习
现有比较成功的网络模型都是依靠大量的标注数据来实现它们的性能,而这些数据是经过了多年的精心收集,通常是有专利的,很少会公开.所以如何利用已经学到的知识去完成不同数据分布的新任务,成为提高深度学习泛化能力的关键.迁移学习就是在解决目标领域具体任务时,无法得到构建模型所需规模的训练数据,故将源领域学习到的知识应用到目标域中去的一种技术.通过使用之前在大数据集上经过训练并表现优秀的预训练模型,将其相应的结构和权重应用到目标域中去,这样不仅大大缩短了训练时间,还避免了由数据规模过小而引发的过拟合现象.图1展示了不同情况下使用预训练模型的方法.
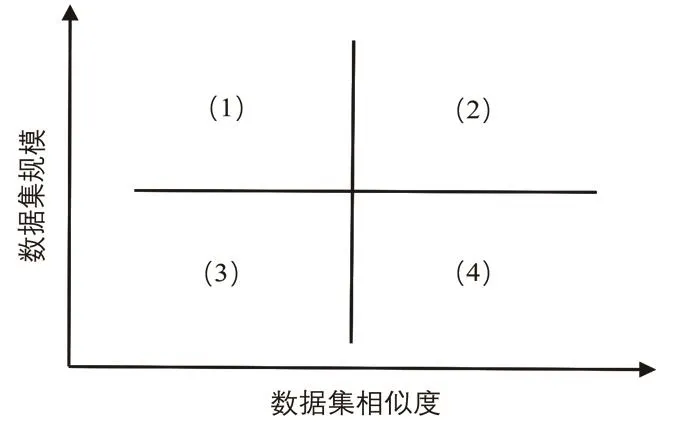
图1 不同情况下的预训练策略
四种预训练方法如下:
(1)该情况下数据集规模较大,数据集相似度较低,由于源领域与目标域数据差异较大,使用预训练模型效果不佳,因此应将模型中的权重全部随机初始化后在新数据集上重头开始训练.
(2)该情况下数据集规模较大,并且数据集相似度较高,这也是最理想的情况,此时保持预训练模型中原有的结构和权重不变,然后在新的数据集上进行训练将非常高效.
(3)该情况下数据集规模较小,数据集相似度较高,此时只需将输出层类别个数改为目标预要求个数,便可达到较高的准确率.
(4)该情况下数据集规模较小,同时数据集相似度也较低,此时可以冻结预训练模型中的前k层的权重,然后重新训练后面的n−k层,相似度不高依靠重新训练来弥补,数据集规模太小依靠冻结部分层权重来弥补.
2 改进方法研究
2.1 过早饱和探究
通过一个例子介绍一下Softmax的饱和情况,设输入的训练数据{(x1,y1),···,(xm,ym)},类别标签yi∈{1,2,···C}.使用SGD训练数据可以得到损失函数和它的偏导数如下

其中zj是Softmax输入向量Z的第j个元素,j∈{1,2,···C}.m输入数据总个数,在yi=j时,1{yi=j}取值为1;在yi/=j时,1{yi=j}取值为0.
为了更直观的分析,我们将多分类Softmax函数化简为二分类的情况,此时类别取值yi∈[1,2],因此我们可以画出二分类情况下Softmax函数及其导数,如图2所示.将横轴设为z1−z2,纵轴设为概率值.将z1>z2的情况定为类别yi=1(z1<z2定为类别yi=2),此时的值更接近于1.当z1>>z2时,P(yi=1|xi)≈1,梯度此时梯度消失无法继续贡献有用信息给反向传播,SGD陷入局部最小中,参数更新结束,模型难以继续优化.为了更直观反映梯度消失情况,将软饱和Softmax函数在z1−z2=0的邻域用一阶泰勒展开来近似,得到硬饱和Softmax函数f(z1−z2),公式如下
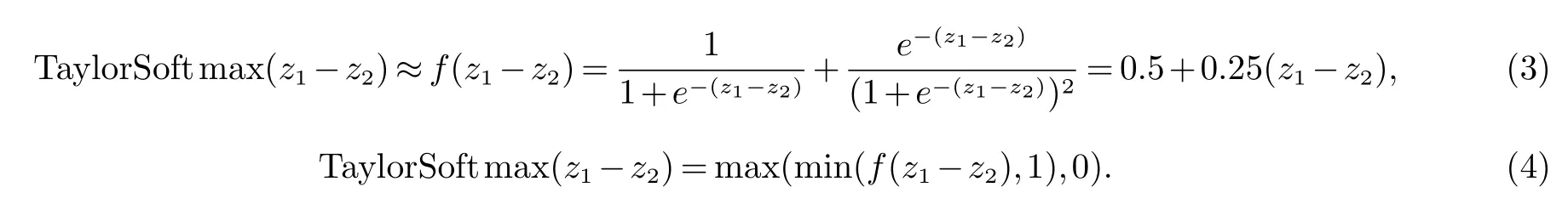
线性近似如公式(4)所示,再对其求导如图3所示,在|x|>5的区域内,硬饱和Softmax已经取值恒为零了.总之,过早的出现饱和会使训练过早的结束,所以应该避免过早饱和情况的发生.

图2 二分类Softmax函数及其导数图

图3 Softmax函数泰勒展开近似及硬饱和示意图
2.2 Softmax加入噪声
为了解决Softmax的饱和导致的梯度过早消失问题,在Softmax的输入zyi中加入合适的噪声来延迟过早饱和.加入噪声的输入应该比未加噪声的输入zyi要小,从而起到延迟饱和的作用,否则便会加快饱和.因此噪声n恒为正值,公式如下

其中n=µ+σξ,ξ∼N(0,1),n服从均值为µ=0,标准差为σ的分布,故变为

让参数σ来控制噪声,训练开始阶段需要较大的噪声来延迟饱和来增加梯度的取值范围,而后面需要较小的噪声来使模型快速收敛.
在DCNN网络模型中Softmax的输入zyi也是全连接层的输出这里Xi是输入的训练数据,Wyi是权重矩阵,byi是偏置向量,由于byi是常数并且zyi主要依赖于所以这里忽略byi.而WTyiXi=||Wyi||||Xi||cosθyi,θyi为两向量||Wyi||和||Xi||之间的夹角,Wyi可以看作是类别yi的分类器,随着训练的进行损失函数降低,它与输入Xi的夹角θyi也逐渐减小,此时需要较小的噪声有助于模型的收敛.让参数σ是一个关于||Wyi||||Xi||和θyi的余弦函数(当θyi减小时cosθyi增大,噪声增大训练将难以收敛,故需要将cosθyi变型为(1−cosθyi)),因此有公式

将(5)式带入到(4)式可得

公式(5)中超参数α用于调整噪声的范围,比较z′yi和zyi中的||Wyi||||Xi||大小,利用(1−cosθyi)去自适应降低噪声的输入加快模型的收敛.加入噪声的Softmax交叉熵损失函数变为

使用标准SGD优化模型时,加入噪声和未加噪声两种情况在计算前向传播和反向传播过程中,只有损失函数中的zyi存在差别.在两种传播中当yi/=j时,计算上没有差别,而反向传播中通过链式法则计算梯度加入噪声后变为

在反向传播过程中中的cosθyi用来表示.
3 实验部分
3.1 数据集介绍
MNIST是由纽约大学Courant研究所提供的一个手写数字数据库,包含6万张训练图片和1万张测试图片,共有10个类别,每张是大小为28×28的灰度图像.CIFAR-10是由Alex Krizhevsky、Vinod Nair和Geoあrey Hinton收集的,包括10个类别的6万张32×32的RGB彩色图像,其中训练图像为5万张,测试图像为1万张.

图4 MNIST和CIFAR-10数据集部分图片
3.2 实验采用模型
VGG模型已成为DCNN中常用的模型结构,它采用多个小尺寸卷积窗口的级联卷积层来代替大尺寸卷积窗口的单个卷积层,这样降低了模型参数减小计算复杂度,同时具有比单个卷积层更强的特征提取能力.网络使用Batch Normalization并采用ReLU作为神经元的激活函数,用均值归一化对数据进行了简单的预处理.所有实验是在Tensorf l ow1.0.1深度学习框架上进行.

表1 各数据集训练所用的DCNN模型结构
表1中2×conv[3*3,64]表示对输入做两次卷积操作,其中卷积核窗口大小为3*3,个数为64.Max pool
ing[2*2]表示采用最大池化的方法,池化窗口大小为2*2.这里所有卷积操作滑动步长stride=1,扩充padding=1,所有最大池化操作的滑动步长stride=2,扩充padding=0.
对MNIST数据集训练过程中数据输入批次为100,学习率恒为0.1,训练集完整迭代10次.CIFAR-10数据集初始学习率为0.1,当训练损失趋于稳定不再下降时将学习率变为0.01,训练集完整迭代20次.模型训练结束后,数据集的测试过程都使用原始未加噪声的Softmax进行分类评估.
3.3 噪声的正负探究
本小节主要探究公式(5)中减去正噪声n=σ|ξ|情况对模型训练的积极影响,并与不加噪声n=0情况,减去高斯噪声n=σξ和减去负噪声n=−σ|ξ|进行比较.本次对比实验使用CIFAR-10数据集,噪声系数选取α=0.01,训练准确率如图(5)所示.

图5 不同噪声情况下训练准确率

图6 不同噪声情况下对应的损失降低变化
从图5中可以看出,加入无噪声和负噪声情况下训练准确率很快升到了85%左右,这表明此时出现了过早饱和的现象,而加入负噪声平均准确率又高于无噪声情况,表明负噪声使Softmax的输入变大,这样一来使饱和更早出现,因此模型训练收敛很快.但从图6中可以看出,加入负噪声时损失值最高,此时更早出现饱和阻碍了SGD产生更宽泛完整的梯度,故而导致最终识别率效果不佳.加入高斯噪声和无噪声情况下,训练准确率是比较接近的,因为高斯噪声服从正态分布均值为零.n=σ|ξ|时训练准确率平均值最低、提升最慢,这表明过早饱和得到了有效延迟,测试错误率中可以看出,此时测试错误率达到了一个更低的值约7.5%,饱和延迟使SGD产生了更为宽泛的梯度,用于反向传播同时收敛速度也就相对变慢,因此花费更多的时间将会促使网络找到全局最小,从而进一步降低测试错误率.总之,只有在Softmax中加入正噪声n=σ|ξ|,才能有效延迟饱和并提高网络模型的整体性能.
3.4 噪声系数探究
前面提过α是控制噪声大小的超参数.加入噪声的Softmax函数,当超参数取值小到α=0时即噪声为零,等同于未加噪声的Softmax函数,随后使用SGD优化将收敛到局部最小时难以逃离,如果没有额外的训练数据,容易导致模型出现过拟合现象.当超参数取值过大,便会导致噪声覆盖掉有用的输入信息,SGD将完全受噪声影响进行随机更新,从而使网络模型无法收敛.因此,超参数α应选取一个合适的值更有助于模型的训练.

表2 不同噪声系数对识别准确率的影响
使用MNIST数据集来探究α不同取值对模型识别效果的影响,如表2所示.当α=0时,z′yi=zyi相当于未加噪声.α=0.1时在两个数据集上都达到了最低的错误率,相比不加噪声的原始Softmax的准确率有所提高.当α取到1时,准确率相比不加噪声情况,出现了降低的现象,这是由于噪声过大淹没了部分有用信息,并且收敛时间也会增长.综上所述,证明了选取合适的超参数α的值,加入的噪声将有助于提高SGD探索能力,使模型损失收敛至全局最优,从而改善DCNN模型的准确率.
3.5 预训练模型应用
使用CIFAR-10数据集来探究最佳预训练方法,首先CIFAR-10数据集(5万张图片)规模相比ImageNet(120万张图像)算是一个小数据集,同时ImageNet的1 000类图片主要来源于我们的日常生活,包括各种动物、家庭用品、通勤工具等,而CIFAR-10只包括4种通勤工具和6种常见动物,因此两个数据集的相似度较低.所以此情况选取2.2节中介绍的第四种预训练方法.
情况1:不使用预训练模型,模型卷积层和全连接层全部参数进行随机初始化.
情况2:冻结前4个卷积层,使它们使用预训练模型中的参数,其余卷积层和全链接层随机初始化后重新训练.
情况3:冻结前7个卷积层,然后操作与情况2一样.
情况4:冻结前10个卷积层,然后操作与情况2一样.
情况5:冻结前13个卷积层,然后操作与情况2一样.

图7 五种预训练策略准确率走势

图8 五种预训练策略损失变化情况
训练准确率如图7所示,可以明显看出各种情况训练迭代26个epoch后,未使用预训练模型参数的情况5准确率提升缓慢最终只有约47%,而其他几种情况随着网络模型冻结的卷积层减少,准确率在稳定提高,当模型中所有卷积层都使用预训练模型参数,而只去训练全连接层的参数时准确率达到了最高约92%.五种策略的损失降低情况如图8所示,最终准确率结果见表3.
不同预训练策略的耗时情况如图9所示,这里统计了除情况1的所有情况在CIFAR-10数据集上准确率达到90%时所需要的时间.从图中可以看出,随着冻结的卷积层越多,达到相同准确率所需时间越少.而情况1是不采用预训练模型中的参数进行重新训练,实验经过30h后准确率只有约60%,但损失仍有下降趋势,继续训练依然可以提供效果,但需要更长的时间.因此,实验充分证明了采用预训练模型可以在提高分类性能的同时缩短训练时间.

表3 不同预训练策略在26次迭代后的准确率

图9 准确率达到90%所需训练时间
3.6 方法比较
对比NiN、Maxout、DSN方法在MNIST和CIFAR-10数据集上的实验结果如表4所示.本文在MNIST数据集上采用表1中网络结构,学习率为0.001,噪声系数取值0.1,经过20次的迭代,本文方法达到了99.67%的准确率.在CIFAR-10数据集上同样采用表2中对应的VGG网络模型,这里学习率为0.005,噪声系数取值0.1,采用情况5对应的预训练策略,经过25次迭代后达到了92.35%的准确率,可以看出本文方法在两个数据集上的实验效果明显优于其他方法.

表4 两个数据集上不同方法对比
4 结束语
本文通过在Softmax中注入噪声来延迟饱和,使正向传播过程产生更为连续和完整的梯度,从而提高随机梯度下降法SGD找到网络全局最小的机会;探究了非负噪声的必要性、最佳噪声超参数取值和不同数量参数迁移的影响;最后借助迁移学习概念,利用预训练模型参数来代替随机初始化参数,使准确率提高并有效防止了过拟合问题.在公开数据集上的实验结果表明:本文所提改进方法具有良好的识别性能和较强的泛化能力.
参考文献:
[1]Ren S,He K,Girshick R,et al.Faster R-CNN:Towards Real-Time Object Detection with Region Proposal Networks[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2015,39(6):1137-1149.
[2]ˇSevo I,Avramovi A.Convolutional Neural Network Based Automatic Object Detection on Aerial Images[J].IEEE Geoscience&Remote Sensing Letters,2017,13(5):740-744.
[3]Wen Y,Zhang K,Li Z,et al.A Discriminative Feature Learning Approach for Deep Face Recognition[C].European Conference on Computer Vision,2016:499-515.
[4]Ding C,Tao D.Trunk-Branch Ensemble Convolutional Neural Networks for Video-based Face Recognition[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2017,5:23157-23165.
[5]Simonyan K,Zisserman A.Very Deep Convolutional Networks for Large-Scale Image Recognition[J].Computer Science,2014,2:361-369.
[6]Shankar S,Robertson D,Ioannou Y,et al.Ref i ning Architectures of Deep Convolutional Neural Networks[C].Computer Vision and Pattern Recognition.IEEE,2016:2212-2220.
[7]Goodfellow I J,Warde-Farley D,Mirza M,et al.Maxout Networks[J].Computer Science,2013,28:1319-1327.
[8]Raymond F E,Raymond B W.Fractional Max-Pooling[J].Theoretical Economics Letters,2015,5(2):225-237.
[9]He K,Zhang X,Ren S,et al.Delving Deep into Rectif i ers:Surpassing Human-Level Performance on ImageNet Classif i cation[C].IEEE International Conference on Computer Vision.IEEE,2016:1026-1034.
[10]Krizhevsky A,Sutskever I,Hinton G E.ImageNet classif i cation with deep convolutional neural networks[C].International Conference on Neural Information Processing Systems.Curran Associates Inc,2012:1097-1105.
[11]Huang G,Liu Z,Weinberger K Q.Densely Connected Convolutional Networks[C].Computer Vision and Pattern Recognition.2016:1364-1376.
[12]Nair V,Hinton G E.Rectif i ed linear units improve restricted boltzmann machines[C].International Conference on Machine Learning Omnipress,2010:807-814.
[13]Gulcehre C,Moczulski M,Denil M,et al.Noisy activation functions[C].International Conference on Machine Learning,JMLR org,2016:3059-3068.
[14]Blundell C,Cornebise J,Kavukcuoglu K,et al.Weight Uncertainty in Neural Networks[J].Computer Science,2015,5:324-332.
[15]Neelakantan A,Vilnis L,Le Q V,et al.Adding Gradient Noise Improves Learning for Very Deep Networks[J].Computer Science,2015,12:117-125.
[16]Lin M,Chen Q,Yan S.Network In Network[J].Computer Science,2013,14:482-490..
[17]Lee C Y,Xie S,Gallagher P,et al.Deeply-Supervised Nets[J].EprintArxiv,2014,6:562-570.

