贫困地区经济发展与教育扶贫关系分析——基于湖南省湘西州的实证

向延平

（湖南女子学院旅游系，湖南长沙410004）

一、引言

在经济发展与教育发展、教育扶贫间关系的协整研究成果方面，邓宏亮、黄太洋[1]运用空间面板回归和门槛面板回归模型对2000-2010年省级面板数据进行分析，探讨了经济发展中教育投入效应的空间外溢性及门槛特征。关晓斌[2]通过实证研究1996-2011年间北京地区高等教育投入与经济发展指标时间序列数据，验证了北京地区高等教育投入和经济发展指标之间存在明显的长期均衡关系。赵国春、梁勇[3]通过研究少数民族地区高等教育与经济发展协同性关系，发现总体上少数民族地区高等教育与当地经济发展的协同性逐年降低。高晓盼、赵秀恒[4]利用ARMIA模型、格兰杰因果检验、Johansen协整检验和向量误差修正模型（VEC）实证分析1985-2011年我国城市化进程中城市化、经济发展与高等教育水平发展情况。陶元磊、李强[5]引入高等教育其他外部治理主体为辅助变量，运用1999-2011年间31个省份面板数据，以空间相关性为基础，构建动态 VECM 模型分析两者之间长短期因果关系和强因果关系。本文以地处贫困地区的湖南省湘西土家族苗族自治州（简称湘西州）为例分析其经济发展与教育扶贫关系。

二、研究方法与数据来源

我们使用的脉冲响应模型[6]是向量自回归（VAR）模型和脉冲响应函数（IRF）。为了充分考虑研究数据统计特征，VAR模型数学公式为：

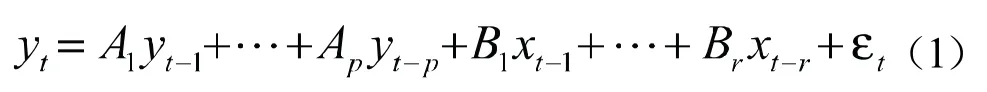
公式（1）中，yt：m 维内生变量向量；xt：d 维外生变量向量；p：内生变量的滞后阶数；r：外生变量的滞后阶数；A1…At和 B1…Br是待估参数矩阵；et：误差向量，t：年。

本文选取湘西州2005-2015年财政收入（FR）和教育资助（EA）两个指标展开分析，数据来源于历年湘西州《统计公报》，见表1。为避免异方差影响，我们将FR、EA所有数据进行自然对数变换，分别表示为LFR、LEA，其对数一阶差分分别表示为DLFR、DLEA。利用 Eviews8.0统计软件完成本文数据处理与检验。

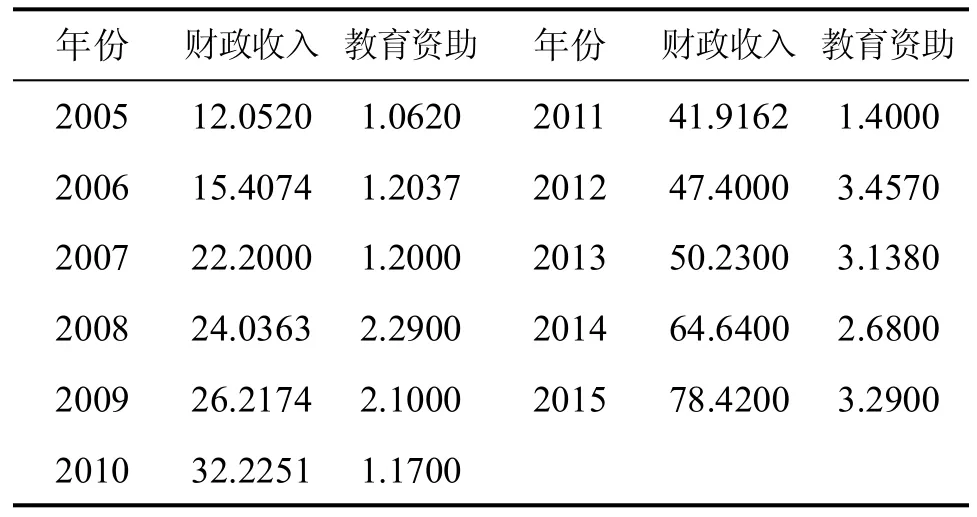
表1 湘西州财政收入与教育资助数据（单位：亿元）

三、研究结果与分析

1.序列图分析

LFR、LEA变化趋势图见图1，可以看出，LFR、LEA均呈现出连续增长的趋势，表明LFR、LEA两个序列是带有增长趋势的非平稳序列。由图2判断出DLFR、DLEA即LFR、LEA的一阶差分存在平稳性，于是我们对其进行VAR模型平稳性检验。

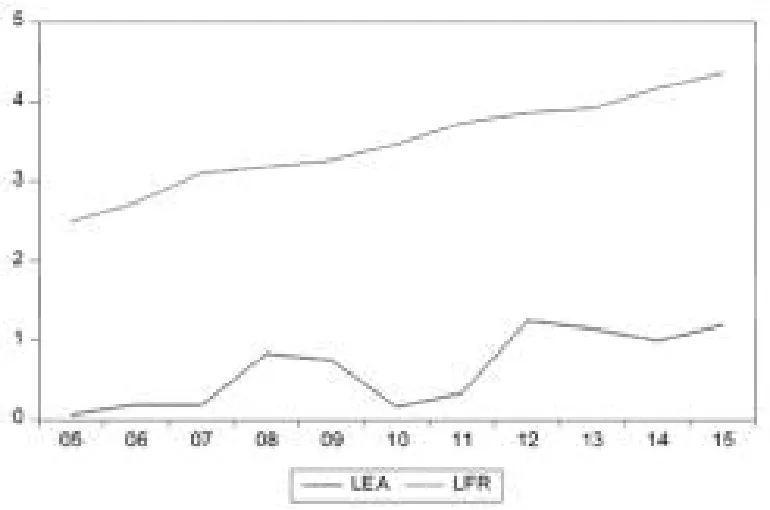
图1 LFR、LEA变化趋势

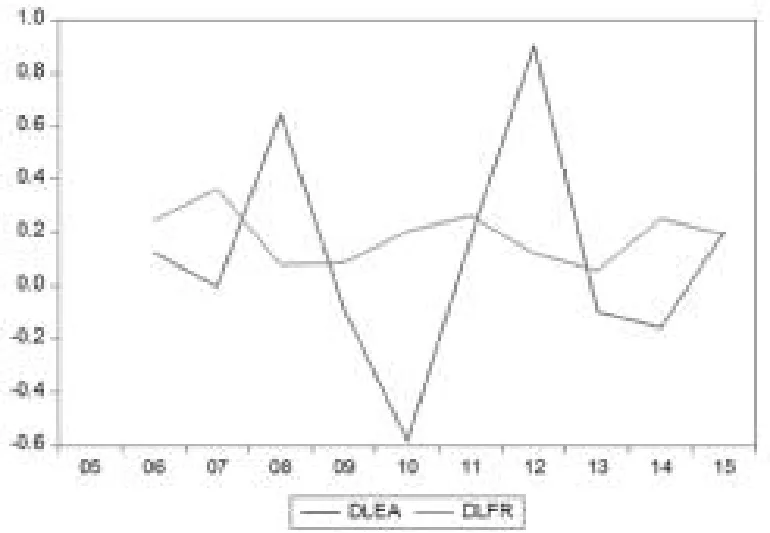
图2 DLFR、DLEA变化趋势

2.VAR模型平稳性检验

图3 LFR、LEA的AR根图

图3为LFR、LEA数据的VAR模型平稳性检验结果图，图中显示出全部特征根均小于1，表明LFR、LEA是一个平稳系统，呈现出平稳性特征。

3.VAR模型滞后期的选择

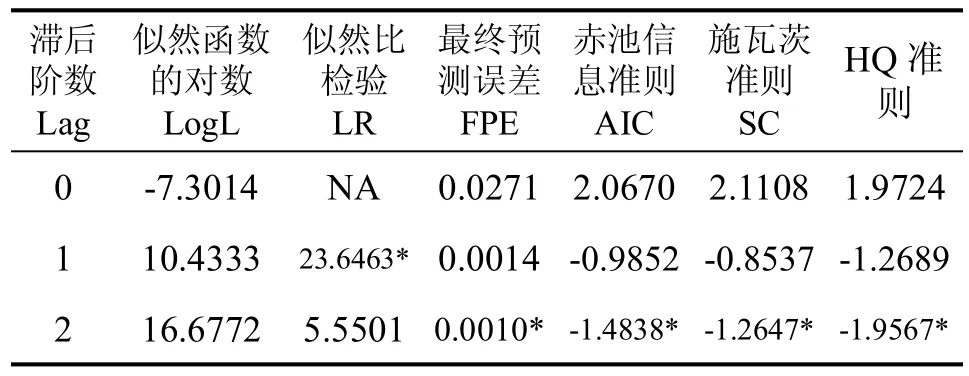
表2 VAR模型不同滞后期评价指标值

从表2中看出，VAR模型不同滞后期5个评价指标值（LR、FPE、AIC、SC、HQ）中有4个指标（FPE、AIC、SC、HQ）认为应建立VAR（2）模型，于是我们决定建立VAR（2）模型展开分析。

4.VAR模型估计

前文分析结果说明LEA、LRF是一个平稳数列，故我们应建立VAR（2）模型，见表3。

表 3 LEA、LRF 的 VAR（2）模型

进而我们得到VAR（2）模型的代数表达式，见公式（2）、（3）：

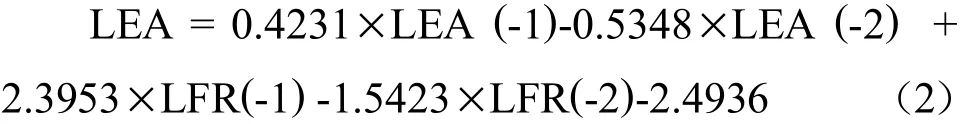
5.脉冲响应分析

LEA、LFR脉冲响应分析过程中，我们选择的CombinedGraphs（合成图）和None（非算法），同时假设冲击作用的滞后期是10年。

图5（1）是LEA对一个标准差新息的响应。由图5（1）可看出，LEA对自身的新息过程比较敏感，在受到单位冲击后立刻产生反应，呈现下降趋势，在第2期接近零，之后递减至第3期达到最低点，之后回升至第5期，第5期至第7期呈现下降趋势，第7期到第9期呈现回升趋势，总体呈现波动起伏状态，整体说明LEA对LFR呈现正响应。LFR对LEA的一个标准差冲击在初始期呈现零响应，第2期后递增达到最大，之后递减到第4期，第4期到第6期上升后下降到第8期，第8期持续上升，在冲击期间内也呈现波动起伏状态，同样整体说明LEA对LFR呈现正响应。

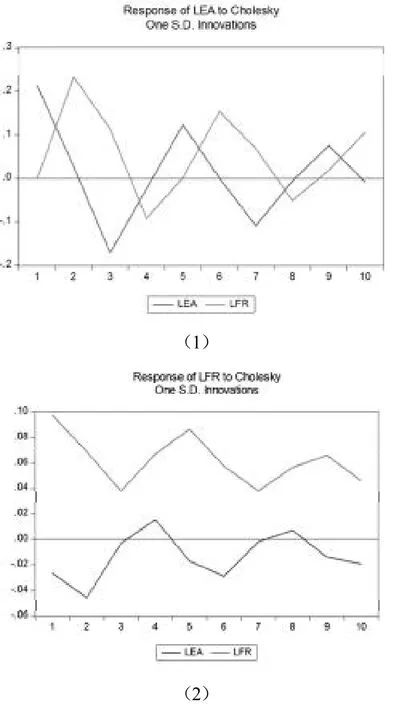
图5 LEA、LFR对一个标准差新息的响应

图5（2）是LFR对一个标准差新息的响应。由图5（2）可看出，LFR对其自身的一个标准差一开始处于零之下，虽有波动，但全部呈现出正响应。LFR对于LEA标准差的扰动一开始达到最高点，此后起伏不平，说明LFR对LEA呈现正响应不太显著。

6.格兰杰（Granger）检验

Granger因果关系检验结果见表4，滞后期为2时，FR不是 EA格兰杰成因的原假设拒绝，即说明FR是EA的格兰杰成因；同理，EA不是FR格兰杰成因的原假设拒绝，说明ES是RF的格兰杰成因，可认为EA是FR格兰杰成因的原假设接受。总之，ES和RF间存在相互影响关系。

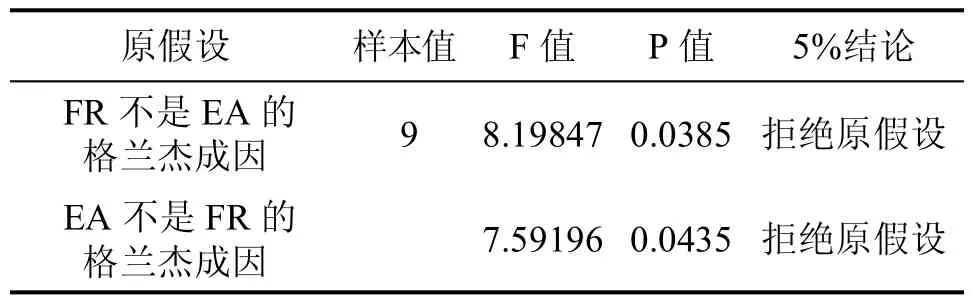
表4 Granger因果检验结果

四、结论

利用VAR模型和脉冲响应（IRF）分析并检验了湘西州2005-2015年财政收入（FR）和教育扶贫资助（EA）之间关系，结果表明：（1）在平稳性建议方面，FR和EA序列存在非平稳性，LFR和LEA序列则存在平稳性，从而我们可建立VAR模型。（2）在脉冲响应方面，LEA对LFR呈现正响应，LFR对LEA正响应不太显著，说明湘西州经济发展对教育扶贫产生了正面影响，湘西州教育扶贫对经济发展的正面影响不太明显。（3）在格兰杰成因方面，滞后期为2时，FR和EE之间存在相互影响；EA是FR的格兰杰成因，FR也是EA的格兰杰成因，结果说明湘西州经济发展促进了当地教育扶贫，教育扶贫同样促进了当地经济发展。

我们建议：（1）湘西州应充分利用当地经济资源，积极发展当地经济，促进旅游、矿产、特色农业等产业发展，增加政府财政收入，改善当地经济生态和教育环境，提高当地居民收入水平、生活水平和教育水平，以经济促教育，通过发展当地经济促进当地教育扶贫。（2）加大湘西州教育扶贫，提高教育资助力度、额度、广度和深度，扩大教育资助覆盖面，全面落实教育精准扶贫，重点是学前教育精准扶贫、中学教育精准扶贫和职业教育精准扶贫，做到教育扶贫对象精准，教育扶贫方式精准，精准管理教育扶贫资金，实现湘西州教育真扶贫和扶真贫，改善湘西州教育生态，全面提高贫困地区居民智力和技能，提升贫困居民教育水平和技术技能，以此促进当地经济发展，做到贫困地区真脱贫和脱真贫。

参考文献：

[1]邓宏亮，黄太洋.经济发展中教育投入效应的空间计量与门槛分析[J].中国高教研究，2013，（3）:25-31.

[2]关晓斌.北京地区高等教育投入与经济发展协调关系研究[J].中国人民大学教育学刊，2014，（4）:117-127.

[3]赵国春，梁勇.少数民族地区高等教育与经济发展的协同性研究[J].中国高教研究，2014，（5）:58-64.

[4]高晓盼，赵秀恒.城市化、经济发展与高等教育水平的实证研究[J].统计与管理，2014，（6）:43-44.

[5]陶元磊，李强.地方高等教育财政投入与区域经济发展的协同效应研究——基于省际面板数据的空间因果性分析[J].复旦教育论坛，2015，（1）:74-81.

[6]易丹辉.数量分析与Eviews应用[M].北京：中国统计出版社，2002.167.