基于两层压缩感知的频率—角度联合估计方法
魏爽 陶春贵 李莉 蒋德富


摘要: 介绍了一种基于两层压缩感知的频率/角度联合估计方法,第一层压缩感知算法采用单快拍模型求解方向波数,第二层压缩感知算法利用方向波数形成的参数逆矩阵求解频率参数,以此求得角度.为验证所提方法的性能,利用3路不同频率和角度的信号分别在不同信噪比(SNR)、快拍条件下对信源频率/角度进行估计.仿真实验结果表明:该方法在少快拍条件下可对信源的频率和角度进行精确估计.
关键词:
两层压缩感知; 频率估计; 角度估计; 方向波数; 信源定位
中图分类号: TN 911文献标志码: A文章编号: 10005137(2018)02017907
Frequency and DOA joint estimation method based on
twolayer compressed sensing
Wei Shuang1,2, Tao Chungui2, Li Li1, Jiang Defu2
(1.The College of Information,Mechanical and Electrical Engineering,Shanghai Normal University,Shanghai 200234,China;
2.College of Computer and Information,Hohai University,Nanjing 211100,China)
Abstract:
A frequency and angle joint estimation method based on twolayer compressed sensing is introduced.The first layer uses single snapshot model to solve the direction wave number,and the second layer uses the inverse of the parameter matrix to solve the frequencies,so as to obtain angel parameters.In order to verify the performance of the proposed method,signals of three different frequencies and angles were used to estimate the source frequency/angle under different singal noise ratio (SNR) and snapshot conditions.Experiments results show that in the condition of few snapshots,the proposed method can obtain the accurate estimation of the source frequency and angle.
Key words:
twolayers compressed sensing; frequency estimation; angel estimation; directional wave number; source location.
收稿日期: 20180201
基金项目: 国家自然科学基金(61401145);江苏省自然科学基金(BK20140858)
作者简介: 魏爽(1983-),女,副教授,主要从事多维信号估计与检测,智能优化和数据挖掘算法,目标定位与识别方面的研究.Email:weishuang@shnu.edu.cn
引用格式: 魏爽,陶春贵,李莉,等.基于两层压缩感知的频率-角度联合估计方法 [J].上海师范大学学报(自然科学版),2018,47(2):179-185.
Citation format: Wei S,Tao C G,Li L,et al.Frequency and DOA joint estimation method based on twolayer compressed sensing [J].Journal of Shanghai Normal University (Natural Sciences),2018,47(2):179-185.
0引言
信源定位是信号处理领域的一个重要问题,在实际应用中,为准确对信源进行定位,常涉及对频率、多普勒频移、波达时间、波达频率等参数的估计.随着通信技术的飞速发展,波达方向和频率联合估计技术广泛应用于雷达、勘探、射电天文、移动通信等领域,成为了信号处理领域的一个热点问题[1-6].
自从波达方向和频率的联合估计方法问世以来,学者们提出了许多同类方法.文献[7]提到一种基于空域滤波的频率和方向波数配对方法,该方法具有简单可行的优点.为提高方向波数估计精度,文献[7-9]提出基于信号奇异值分解的压缩感知方法,使空域滤波法在低信噪比(SNR)条件下的稳健性大大增强.
压缩感知理论(CS)是一种新的高分辨求解算法,大量文献研究表明该方法在低信噪比、少快拍数条件下对参数估计的稳健性较好[10-13],基于此,本文作者提出了一种两层压缩感知的频率/角度估计方法.通过利用压缩感知理论对方向波数和频率的求解,提高算法在低信噪比、少快拍条件下对信源定位的精确度.
1信号模型
假設有P个远场信号分别以θ1,θ2,θ3,…,θP角度入射到阵元数为N,阵元间距为d的均匀线阵上[1-8,14],信号对应的中心频率分别为f1,f2,f3,…,fP,则第i个信号(i=1,2,3,…,P)角度和频率的二维导向矢量
a(θi,fi)=[1exp[(-j2πfidsinθi)/c…exp[(-j2π(N-1)fidsinθi)/c]]T,(1)
其中,c=3×108 m/s表示光速,由于含有角度和频率信息,求解导向矢量是一个二维求解问题,为将其转化为一维求解问题,设共同含有频率和角度的因子Ki=fisinθi/c,(i=1,2,3,…,P),称K=[K1K2…KP]为方向波数.那么,
a(Ki)=[1exp(-j2πdKi)…exp(-j2π(N-1)dKi)]T,(2)
其中,dKi表示第i个信号在相邻阵元间之间的相位差,方向波数对应的阵列流型
A=[a(K1)a(K2)…a(KP)],(3)
其中A为N×P维矩阵.那么第t个快拍时刻线阵接收到的信号为
x(t)=As(t)+w(t),(4)
其中,x(t)N×l为第t个快拍时刻阵列接收的信号矢量,s(t)P×1=[sf1(t)sf2(t)…sfP(t)]T为第t个快拍时刻空间信号矢量,sfi(t)=exp[j2πfit/fs],t=1,2,…,L,fs是采样频率,w(t)N×1为第t个快拍时刻高斯白噪声.由(4)式可得在总共L个快拍中接收到的信号
X=AS+W,(5)
其中,XN×L=[x(1)x(2)…x(L)]为阵列接收信号,SP×L=[s(1)s(2)…s(L)]为L次快拍接收到的空间信号,WN×L为高斯白噪声.
2算法原理
2.1基于压缩感知的方向波数求解
利用联合估计的思想,将二维的频率/角度问题转换为一维的方向波数求解问题,可以大大简化计算复杂度.一些学者们研究发现,若要得到精確的角度估计必须先得到精确的方向波数估计值,虽然以多信号分类(MUSIC)算法为代表的经典谱估计方法[15-16]已能对方向波数进行高分辨估计,但这类算法所需快拍大,计算复杂.压缩感知方法[17-18]以分辨率高,所需快拍数少,利用很少的数据信息即可对信号进行精确恢复的特点,在信号处理领域得到广泛关注.
CS指出当信号具有(或在某个域具有)稀疏性特点时,可利用一个低维矩阵对该稀疏信号进行观测,抽取其中的一部分信息,将高维信号转化为低维信号,通过寻优求解的方法求出最优值.本研究中,方向波数在整个方向波数域内是稀疏的,因此只需利用潜在可能的方向波数值构造出过完备的正交稀疏字典,构造方法为:将整个方向波数域进行等格离栅,分为β个等份,以每一个离栅格点的导向矢量作为变换基矩阵的一个列,构造一个N×β维的变换基矩阵
Ψ=[a(K—1)a(K—1)…a(K—β)],(6)
其中,K—i(i=1,2,…,β)为等格划分后潜在可能的方向波数值,a(K—i)=[1exp(-j2πd—Ki)…exp(-j2π(N-1)dK—i)]T为构造的潜在方向波数导向矢量,那么第t个快拍时刻线阵接收到的信号可被稀疏表示为
x(t)=Ψy(t)+e(t),(7)
其中,y(t)β×1为第t个快拍时刻线阵接收到的信号的稀疏表示,e(t)为高斯白噪声.
高斯随机矩阵能很好地满足约束等距性条件(RIP),被广泛应用于压缩感知方法,因此利用高斯随机矩阵ΦM×N对信号进行观测,观测信号
z(t)=Φx(t)=ΦΨy(t)+Φe(t)=Ty(t)+Φe(t),(8)
其中,z(t)M×1为第t个快拍时刻线阵接收到的信号经过压缩观测后的观测信号,TM×LN为压缩感知恢复矩阵.
在信号满足压缩感知的条件下,通过求解l1范数对(8)式进行求解,数学表达式为
mins-ΦΨy—2+λy—1
(9)
求解模型(9)的算法有多种,本文作者所用信号稀疏度均为已知,以正交匹配追踪(OMP)算法对信号方向波数进行求解.
2.2方向波数和频率的配对算法
在求出信号方向波数后,只需求出信号的频率,然后将频率与方向波数进行配对,即可求出信号频率/角度的二维信息.对于信号频率的求解,有学者提出了基于空域滤波的频率和方向波数匹配的方法[8],利用自适应波束形成算法分别对所求方向波数所对应的信号进行空域滤波并对输出信号利用傅里叶变换(FFT)进行测频,获得每个方向波数所对应信号的频率,即实现信号频率与方向波数的匹配.实验结果表明:此方法可对频率和角度进行较为精确的估计[7-8].
本文作者提出一种基于压缩感知的方向波数和频率配对的估计算法,利用所求方向波数构造方向波数参数矩阵(以下简称参数矩阵)[19]
B=b(K^1)b(K^2)…b(K^P)」,
(10)
其中,b(K^i)=[1exp(-j2πdK^i)…exp(-j2π(N-1)dK^i)]T为求解方向波数导向矢量.用BN×P对阵列接收信号进行改写,改写后的信号(以下简称加参信号)
X^=XT(BT)^+=STAT(BT)^++WT(BT)^+,(11)
其中,X^L×P为加参信号,(BT)^+N×P为BN×P转置的广义逆矩阵,W^L×P为噪声信号,ΩP×P是一个近似于单位矩阵的方阵,称为干扰矩阵,当求解的方向波数越精确,ΩP×P越接近单位矩阵,此时对信号干扰越小,X^L×P就越接近原始信号空间信息.
(11)式所得的加参信号只含有频率信息,且目标频率在整个频域范围内具有稀疏的特性,因此适用于CS理论,可对整个频域进行等格离栅划分,以每一个离栅格点的导向矢量作为变换基矩阵的一个列,构造一个α×L维的变换基矩阵
Ψ^=[s^(1)s^(2)…s^(L)],(12)
s^(t)=[exp(j2πf—1t/fs)exp(j2πf—2t/fs)…exp(j2πf—αt/fα)]T,(13)
其中,f—i(i=1,2,…,α)为等格划分后潜在可能的频率值,s^(t)为潜在频率导向矢量.
均匀线阵经历L个快拍接收到的空间信号频率信息
X^=Ψ^TY^+E^,(14)
其中,Y^α×P为经历L个快拍时刻线阵接收信号的稀疏表示,E^α×P为噪声.利用高斯矩阵对信号进行降维观测得
Z^=Φ^X^=Φ^Ψ^TY^+Φ^E^=T^Y^++Φ^E^
(15)
其中,Z^M×P为L快拍期间线阵接收到的空间信号经过压缩观测后所得观测信号,T^M×α为压缩感知恢复矩阵.由于所得观测空间信號是矩阵形式,且Y^α×P每列只包含一个有用频率信息,只需对每列分别利用OMP算法求解即可得到相应的频率信息.
当求出完整的频率信息后还需对所求频率和方向波数进行匹配,以求解出相应的角度信息,利用所求频率构造匹配矩阵QL×P,将匹配矩阵QL×P中的每个元素与加参信号X^L×P中元素配对,找出最接近两矩阵的匹配矩阵模型,即完成信号频率与方向波数匹配,该匹配方法可以描述为:
minX^-QF
s.t.Q=[q(Y—z(1))q(Y—z(2))…q(Y—z(P))]
,(16)
其中,Y—Z=randperm(f—1f—2…f—P),f—i为所求信号频率(i=1,2,…,P),q(Y^z(i))=[exp(j2πf—i/fs)exp(j2πf—i2/fs)…exp(j2πf—iL/fs)]T为所求频率构造的导向矢量.
根据所求方向波数及频率的匹配情况,即可求出信号角度信息
θ—i=arcsin(K—ic/f—i),(17)
其中,K—i、f—i为相匹配的方向波数和频率.
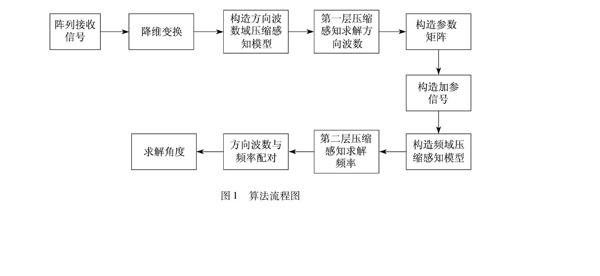
图1为所提出方法的流程图.
3仿真与分析
为衡量算法性能优劣,以空域滤波法为对照,设计了在不同快拍数、信噪比条件下对信号角度和频率进行联合估计的仿真实验,结果表明:所提方法可在信噪比较低的条件下,利用较少的快拍数对信号角度和频率进行精确估计.
为准确评价算法性能采用蒙特卡罗方法对算法进行仿真,利用均方根误差(RMSE)来描述算法的误差.
对实验中所涉及数据做如下规定,角度范围为[-90°,90°],频域范围为0~100 MHz,采用阵元数N=40的均匀线阵,分别选取角度为-20°、20°、45°,频率为40、60、80 MHz的信源,则真实的方向波数分别为-0.0456、0.0684、0.1886.利用单快拍压缩感知模型,采用OMP算法对方向波数进行求解,在求得方向波数后,分别利用相关性匹配、空域滤波及快速傅里叶变换相结合的方法对频率进行估计,在频率求解时以高斯矩阵作为压缩感知测量矩阵,变换基矩阵的维度为100,空域滤波过程中的傅里叶变换离散值取1 024.
3.1实验一
为直观比较所提算法与空域滤波算法对频率估计的性能,先采用OMP算法获得相同的方向波数,再分别用空域滤波法和所提方法估计出信号频率参数.图2(a) 信噪比为30 dB,快拍数L=100,图2(b)中信噪比为10 dB,快拍数L=10.
观察图2(a)、2(b)可发现,空域滤波后用傅里叶变换的方法与本方法均能准确求出信号的频率,在较低信噪比和较小快拍数条件下,空域滤波所得信号频谱能量分散,谱峰不够尖锐,而本算法在相同条件下,依然可以得到较为稳定的频率值.
3.2实验二
为验证本算法在不同信噪比条件下的性能,在快拍数L分别为10、100时,分析不同信噪比对信源频率的误差.不失一般性地,对数据进行500次蒙特卡罗循环.
从图3、4中可以发现,L=10、L=100两种情况对频率、角度估计误差均随着信噪比增大而减小.观察图3发现,同等条件下,两种方法在快拍数较大时对频率估计更加精确,且快拍数较大时,所提方法对频率估计精度优于空域滤波;观察图4 发现,快拍数增加会导致角度估计误差略有增大,而所提方法在两种快拍条件下对角度估计均优于空域滤波法.
对比图3、4发现,同等条件下,所提方法在小快拍数条件下,虽然频率估计误差比空域滤波法略大,但角度估计比空域滤波法更加精确.这是因为方向波数求解过程只用了一个快拍数据,快拍数的多少对方向波数求解没有影响,因此方向波数误差在信噪比相同时,几乎是固定的;方向波数的误差影响角度的求解,对于同一个方向波数值,当频率求解精确时必然导致角度求解误差增大,当频率求解误差大时,角度求解误差小.
4结束语
提出了一种基于两层压缩感知的频率和角度联合估计方法,首先仅使用单快拍信号,结合压缩感知方法求出方向波数估计值,构造方向波数参数矩阵,对参数矩阵求逆,得到信号空间信息.此时空间信息在频域内具有稀疏特性,再利用压缩感知对该空间信息求解得到信源的频率信息,最后需要利用相似性匹配完成方向波数和频率的配对,求出角度参数.该方法可在小快拍数的条件下对信源角度和频率进行精确估计,对于目标探测与识别、水下声呐系统、无线通信等问题的研究具有一定参考意义.
参考文献:
[1]Lemma A N,Van Der Veen A J,Deprettere E F.Analysis of joint anglefrequency estimation using ESPRIT [J].IEEE Transactions on Signal Processing,2003,51(5):1264-1283.
[2]Yun X L,Wei Z X,Bin Z G.Blind joint angle and frequency estimation based on uniform rectangular acoustic vector sensor array [C].Proceedings of the 10th International Conference on Natural Computation,Xiamen:IEEE,2014.
[3]李建峰,张小飞.基于四线性分解的双基地MIMO雷达的角度和多普勒频率联合估计 [J].航空学报,2012,33(8):1474-1482.
Li J F,Zhang X F.Joint estimation of angle and Doppler frequency in bistatic MIMO radar based on quadrilinear decomposition [J].Acta Aeronautica et Astronautica Sinica,2012,33(8):1474-1482.
[4]張小飞,陈华伟,仇小锋,等.阵列信号处理及MATLAB实现 [M].2版.北京:电子工业出版社,2015.
Zhang X F,Chen H W,Qiu X F,et al.Array signal processing and MATLAB implementation [M].2nd ed.Beijing:Publishing House of Electronics Industry,2015.
[5]Wang W Q,So H C.Transmit subaperturing for range and angle estimation in frequency diverse array radar [J].IEEE Transactions on Signal Processing,2014,62(8):2000-2011.
[6]许凌云,张小飞,许宗泽,等.基于任意声矢量传感器阵列的角度和频率估计算法 [J].仪器仪表学报,2012,33(10):2234-2240.
Xu L Y,Zhang X F,Xu Z Z,et al.Novel joint angle and frequency estimation algorithm based on arbitrary acoustic vector array [J].Chinese Journal of Scientific Instrument,2012,33(10):2234-2240.
[7]刘聪锋,廖桂生.基于空域滤波的方向波数域测向测频新方法 [J].电波科学学报,2010,25(1):60-65.
Liu C F,Liao G S.Novel method of angle and frequency estimation in direction wavenumber region using space filtering [J].Chinese Journal of Radio Science,2010,25(1):60-65.
[8]沈志博,赵国庆,董春曦,等.基于压缩感知的频率和DOA联合估计算法 [J].航空学报,2014,35(5):1357-1364.
Shen Z B,Zhao G Q,Dong C X,et al.United frequency and DOA estimation algorithm based on compressed sensing [J].Acta Aeronautica et Astronautica Sinica,2014,35(5):1357-1364.
[9]郑轶松,陈伯孝,杨明磊.一种基于空域滤波的空间临近相干源角度估计方法 [J].电子与信息学报,2016,38(12):3100-3106.
Zhen Y S,Chen B X,Yang M L.Direction of arrival estimation method for spatially adjacent coherent sources based on spatial filtering [J].Journal of Electronics & Information Technology,2016,38(12):3100-3106.
[10]Donoho D L.Compressed sensing [J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[11]Candès E J,Wakin M B.An introduction to compressive sampling [J].IEEE Signal Processing Magazine,2008,25(2):21-30.
[12]Tsaig Y,Donoho D L.Extensions of compressed sensing [J].Signal Processing,2006,86(3):549-571.
[13]Candès E J,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information [J].IEEE Transactions on Information Theory,2006,52(2):489-509.
[14]赵永红,张林让,刘楠,等.一种新的基于稀疏表示的宽带信号DOA估计方法 [J].电子与信息学报,2015,37(12):2935-2940.
Zhao Y H,Zhang L R,Liu N,et al.A Novel method of DOA estimation for wideband signals based on sparse representation [J].Journal of Electronics & Information Technology,2015,37(12):2935-2940.
[15]Asgedom E G,Gelius L J,Austeng A,et al.Timereversal multiple signal classification in case of noise:a phasecoherent approach [J].The Journal of the Acoustical Society of America,2011,130(4):2024-2034.
[16 ]Khan Z I,Kamal M M,Hamzah N,et al.Analysis of performance for multiple signal classification (MUSIC) in estimating direction of arrival[C].Proceedings of 2008 IEEE International RF and Microwave Conference,Kuala Lumpur:IEEE,2008.
[17]Bilik I.Spatial compressive sensing for directionofarrival estimation of multiple sources using dynamic sensor arrays [J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(3):1754-1769.
[18]Rossi M,Haimovich A M,Eldar Y C.Conditions for target recovery in spatial compressive sensing for MIMO radar [C].Proceedings of 2013 IEEE International Conference on Acoustics Speech and Signal Processing,Vancouver:IEEE,2013.
[19]顧建峰,魏平.基于伪协方差矩阵的频率和角度联合估计算法 [J].通信学报,2007,28(8):40-45.
Gu J F,Wei P.Joint frequencyangle estimation using a pseudocovariance matrix [J].Journal on Communications,2007,28(8):40-45.
(责任编辑:顾浩然,包震宇)

