三向预应力混凝土连续箱梁桥横向加劲肋拓宽研究

吴文清，翟建勋，张 娴，赵 昊，*，张 慧

（1.东南大学交通学院，南京 210096；2. 中铁工程设计咨询集团有限公司，北京 100055）

近十多年来，随着高速公路交通量的逐年增加，我国高速公路已经出现了比较严重的交通拥堵现象，影响了道路的通行能力和服务水平，因此，对原有道路进行拓宽改造已经迫在眉睫。目前，高速公路拓宽基本采用在原有高速公路两侧进行横向拓宽改造，可有效控制横向拓宽的建设成本[1-2]。在预应力混凝土箱梁桥横向拓宽拼接时，如果新旧箱梁采用直接拼接，通常需要纵向切割部分待横向拼接的既有箱梁翼缘板，以扩大翼缘板板端横截面积，便于横向植筋施工[3-4]。不过这种拼接方案并不适用于三向预应力混凝土箱梁桥的横向拓宽，因为在三向预应力混凝土箱梁桥的翼缘板内，横向预应力钢筋的存在使其不能被纵向切割。因此，对于三向预应力混凝土箱梁桥的横向拓宽工程，至今尚无可被广泛接受的合理拓宽方案[5-6]。

目前，针对这种连续箱梁翼缘板横向拼接的困难，在实际工程中一般有两种解决方案[7，11]。

（1）采用新旧翼缘板结构分离的方案。根据结构分离的横向拓宽设计要求，设置纵向伸缩装置能够满足新旧结构之间的横向和竖向变形要求，保证桥面平顺，且能够承受车辆的反复碾压而不损坏。例如中国银川黄河大桥[7-8]、伊朗Bozorgmehr 大桥[9]等拓宽工程，即采用了新旧主梁结构不连接的横向拓宽连接方案。经现场调查，银川黄河大桥共930 m（12×30 m+60 m+5×90 m+60 m）范围内新旧桥上部结构之间沿纵向预留2 cm宽缝隙，然后通过纵向伸缩装置将新旧桥面连接在一起，使得桥面平顺。调查发现，银川黄河大桥拓宽中采用了3种伸缩缝装置，分别为弹塑体无缩缝伸缩装置、JFC减振防滑伸缩装置、EMR树脂弹性混凝土伸缩装置。上述分离方案结构简单，但缺点也很明显，有证据表明[9]，尽管相互分离但新旧箱梁之间仍然存在相互动力作用，也无法有效控制新旧结构之间的变形差，易导致桥面铺装开裂破坏并造成高速行车安全事故。

（2）采用横向刚性连接的拼接方案。如沪宁高速公路塘河大桥横向拼接即采用了如图1所示的刚性连接方案[10-11]。由于横向刚性连接结构的刚度较大，新桥基础沉降对旧桥结构受力产生十分不利的影响。在软土地基条件下，新旧桥梁之间的沉降变形差比较明显，将会给拓宽结构桥梁的安全带来较大的不确定性。

针对上述软土地基条件下三向预应力混凝土连续箱梁桥的横向拼接难题，本文以京沪高速公路盐河大桥为研究背景，提出了一种新型横向拼接结构，并申报了发明专利“一种三向预应力混凝土连续箱梁桥的横向拓宽拼接结构”（申请号： 201510055081.X）。在保持新旧箱梁翼缘板结构分离的前提下，在新、旧箱梁翼缘板下侧增设沿纵向均匀设置的横向加劲肋群，将新旧箱梁翼缘板连接起来，而不用凿除设置有横向预应力钢筋的部分翼缘板，形成一种柔性的横向拼接结构，以达到该类箱梁桥横向拼接的目的，如图2所示。新旧箱梁结构横向拼接完成以后，借助于横向加劲肋群作为其横向传力途径，来传递新旧箱梁之间的相互作用，同时能够适应新旧基础较大的不均匀沉降差变形。相比于方案（2），加劲肋的刚度较小，适合华东及华南地区的软土地基。作为横向拼接结构的加劲肋，虽然只是常规的结构，但是把横向加劲肋应用于软土地基地区箱梁拓宽中是一种结构创新，它既能避免双箱梁结构横向分离所带来的结构变形差导致的交通安全问题，又是一种有效的横向连接结构形式。只要选择合适的结构刚度很有可能解决新旧箱梁之间较大变形差所带来的结构受力安全问题。需要特别强调的是，在软土地区进行箱梁桥横向拓宽时，面内刚度巨大的横隔板是不宜采用的一种结构形式，但是加劲肋由于抗弯刚度较小且易于调节刚度，非常适用于软土地区箱梁桥的横向拓宽中。为此，本文利用有限元方法重点分析横向加劲肋在各不利荷载作用下的受力状况，并通过简化模型进行理论分析，同时建立加劲肋局部有限元模型，分析加劲肋尺寸和间距的影响，以探讨该横向拼接结构的可行性。

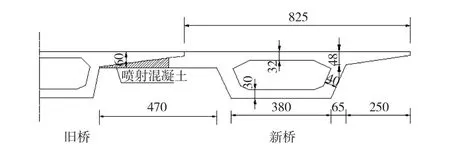
图1 塘河大桥横向拼接方案（单位：cm）

图2 盐河大桥箱梁拼接结构及尺寸（单位：cm）

盐河大桥位于淮江高速公路K7+550～K8+550路段，跨盐河和规划淮涟一级公路，原桥已于20世纪90年代末完成施工。盐河大桥跨径布置为（42+65+42）m，是采用悬臂现浇施工的三向预应力变截面连续箱梁桥。主梁结构采用C50混凝土，预应力钢束为7Φ5钢绞线。

原桥采用双向分离式车道，单幅桥面宽度为13.5 m，拓宽后桥面宽度为20.5 m。为了避开翼缘板横向预应力钢筋对翼缘板纵向切割的阻碍，拟采用增设横向加劲肋群的方式将新旧箱梁翼缘板连接起来。新旧箱梁翼缘板之间依然保留结构缝，结构不连接；同时采用在新旧箱梁拼接侧翼缘板底侧植筋或预留钢筋的形式布置钢筋骨架，现场搭支架，现浇混凝土加劲肋，从而将新旧箱梁翼缘板连接在一起。植筋时避开横向预应力钢筋位置。为保证施工质量，建议采用自密实混凝土。盐河大桥横向拼接方案如图2所示。加劲肋沿着结构纵向每隔一定间距连续布置。在通过初步分析之后，拟定横向加劲肋尺寸为：高度H=30 cm，厚度B=50 cm，纵向布置间距L=4 m。

1 加劲肋拼接拓宽结构对外界作用差异性的反应研究

由于建造时间有差异，导致新旧桥结构之间存在材料收缩和徐变变形差、基础不均匀沉降差等明显差异性作用，这些差异将引起新旧桥之间强烈的相互作用，同时，车辆偏载作用将对既有桥梁的内力状态产生附加差异影响。本文讨论的外界差异性作用主要有3类：新旧桥梁的材料收缩及徐变变形差、新旧桥梁基础沉降差和车道荷载。本文首先采用有限元分析方法对此展开分析研究。

1.1 有限元模型建立和加载工况

采用Midas civil建立实体有限元模型，混凝土结构采用8节点六面体实体单元，预应力钢筋采用植入式钢筋模拟，将钢筋的刚度添加到混凝土母单元中，未考虑普通钢筋对结构刚度的影响。新、旧箱梁均采用C50混凝土，预应力钢绞线张拉控制应力为1 395 MPa。

有限元模型定义了施工阶段，并模拟施工过程中及成桥后的边界条件。有限元模型中混凝土收缩徐变特性基于《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62—2004）考虑了收缩、徐变等混凝土时间依存材料特性。全桥有限元模型共有597 688个单元，758 545个节点。模型中总体坐标系的原点位于旧桥箱梁左边跨梁端支点截面外侧翼缘根部；x轴沿桥梁纵向，以向右为正；y轴沿桥梁横向，以旧桥方向为正；z轴沿桥梁竖向，以向上为正。

本文主要针对以下3个工况进行分析：

工况1：新建桥梁的材料收缩及徐变作用；

工况2：新建桥梁基础沉降作用；

工况3：车辆活载偏载作用。

1.2 加劲肋结构及主梁受力状态分析

由于横向加劲肋是横向拼接结构的关键构造，因此，本文重点分析加劲肋在上述各工况下的受力特性，包括变形特点和应力分布状态，以研究采用该柔性横向拼接结构的可行性。最后，本文分析了横向拼接对既有箱梁结构的纵向内力影响规律。

1.2.1 工况1：新建桥梁的材料收缩及徐变作用

假设拓宽时旧桥的收缩、徐变作用已基本完成，有限元模型中只考虑新建桥梁的混凝土收缩和徐变变形；当新旧结构通过加劲肋连接在一起时，新桥产生的收缩、徐变变形将会受到旧桥的结构约束，从而在新旧主梁之间产生相互作用内力和结构变形。为了减轻该附加内力作用，拓宽工程中一般在新桥施工完成3个月以后再将新旧箱梁连接在一起。在上述附加内力作用下，分析计算拓宽结构运营10年后的结构应力状态。本文着重分析主梁结构横向变形和加劲肋主拉应力状态。

（1）主梁横向变形

由于新旧箱梁之间的横向拼接作用，新桥主梁的纵向回缩变形受到旧桥主梁的约束，导致新旧梁体产生共同的横向变形，该横向变形方向偏向新桥一侧。假如横向固定约束设置在中间支座处，将使梁端在平面上出现明显的横向位移，导致梁端向外侧移动，横向位移最大值Δ=51 mm。为防止支座发生剪切破坏，桥梁拓宽施工中应采用剪切变形能力强的支座。整体变形使得旧桥主梁偏心受压，新桥主梁以及拼接加劲肋呈偏心受拉状态。

对于这种长联桥梁拓宽, 为了避免梁端过大的横向变形挤压侧向抗震挡块，相关文献[14-15]对长联多跨连续箱梁桥的横向拓宽提出了若干解决方案，如限制拼接拓宽的桥梁总长以避免出现较大的横向变位，或者沿桥长方向的中段采用拼接拓宽方案，每联端部1/3桥长范围内分离的局部横向拼接方案等思路，但方案都不够成熟。

（2）加劲肋纵向应力状态（x轴向）

新旧混凝土收缩、徐变差异作用下，使横向加劲肋呈现出复杂的应力状态。由于梁端横向变形最大，本文主要对靠近梁端的横向加劲肋应力状态进行分析。对于横向加劲肋的受力状态，从纵向（x轴向）和横向（y轴向）分别分析结构的应力状态。

靠近梁端的第1根和第2根加劲肋x轴向应力分布图如图3所示，图中应力单位为MPa，位于实体边线上方的是拉应力，位于实体边线下方的是压应力。

由于新箱梁回缩变形，旧箱梁通过加劲肋限制这种变形，因此在加劲肋与箱梁的接触面均出现拉应力，这种受力状态出现在边支座附近位置，影响范围持续到距离边支座第3个加劲肋（距离边支座约为14 m），加劲肋底部大部分处于受压状态。由图3可知，加劲肋x轴向最大拉应力出现在边支座截面位置处旧桥一侧端部，最大拉应力达到了1.6 MPa，且最大拉应力由边支座截面向跨中方向逐渐减小，距离边支座处第2个加劲肋的最大拉应力值降到了1.2 MPa。

图3 加劲肋顺桥向（x轴）正应力（单位：MPa）

（3）加劲肋横向应力状态（y轴向）

加劲肋的y轴向正应力分布如图4所示，图中应力性质与图3相同。

图4 加劲肋横桥向（y轴向）应力分布（单位：MPa）

由图4可知，收缩、徐变作用下，拼接加劲肋上下翼缘的横桥向基本处于受拉状态，拉应力峰值出现在旧桥侧加劲肋端部，其中边支座位置处的加劲肋拉应力值达到了2.1 MPa。加劲肋呈现拉应力的原因为：旧箱梁是在新箱梁的拉动下向新箱梁一侧横向变形，结果就呈现出新旧箱梁之间通过加劲肋传递横向拉力。

基于上述分析，可以认为横向加劲肋与既有箱梁腹板的交界面处产生了较大的拉应力，存在较大的开裂可能性。

1.2.2 工况2：基础不均匀沉降差作用

结构拓宽时，假设旧桥基础的沉降已经历多年且基本完成，而新桥基础的沉降还未完成，因此将产生新旧桥基础的不均匀沉降差，如图5所示，从而在新旧主梁之间产生附加的相互作用力。

图5 新桥支点沉降箱梁变形

分析时仅考虑新桥基础沉降，按整体沉降差5 mm考虑，该数据是参照有关的计算分析资料和实地沉降观测资料拟定而成[16]。分析表明，基础不均匀沉降差作用对结构产生的内力影响主要体现在靠近支座位置附近的结构。图6为主要控制截面的横向正应力图，应力单位为MPa。

图6 沉降差导致拼接部位的横向正应力分布（单位：MPa）

分析表明，新桥一侧加劲肋或翼缘板底部均出现拉应力，边支座截面处最大拉应力达到5.3 MPa，中支座截面处拉应力达到4.89 MPa，上述拉应力值均大于材料抗拉强度，而旧桥翼缘顶面在边支座截面处拉应力达2.52 MPa，中支座截面处拉应力也达到2.17 MPa。对于无加劲肋截面位置处，应力分布规律十分类似，但是相应应力值明显减小，说明支座沉降所造成的其他截面结构拉应力状态远小于支座截面应力状态，所以重点关注支座截面即可。

由于软土基础的基础沉降将历经很长一段时间，即基础沉降给混凝土横向拓宽结构的内力影响是长期的，因此在计算中应考虑混凝土应力松弛效应。按照文献[17，21]的研究成果，结构应力可进行折减, 本文建议折减系数可取0.45。基于上述因素，边支座截面处新桥翼缘底部拉应力可降低为2.35 MPa，中支座截面处相应拉应力降低为2.20 MPa。显然上述最大拉应力值小于C50等级混凝土的抗拉强度标准值2.65 MPa。尽管如此，还需在相应位置采取加强措施来降低混凝土开裂的危险性。

1.2.3 工况3：车辆活载偏载作用

本节研究在车道荷载作用下，横向拼接结构所承受的横向应力分布状态，重点是横向加劲肋的受力特性。因此，车道荷载的横向分布主要考虑在旧桥箱梁侧偏载布置。盐河大桥拓宽前的桥面宽度为13.5 m，单向2车道布置，外加1个紧急停车带。分析计算中采用新规范中规定的公路-Ⅰ级车道荷载进行加载，可考虑按3车道进行纵向加载，拓宽拼接前后的荷载横向分布如图7所示。纵向布置以中跨跨中截面挠度最大原则进行布载。

图7 车道荷载横向分布（单位：m）

（1） 结构位移分析

拓宽前后新旧桥主梁在相同活载作用下的竖向变形如图8所示，计算过程中未考虑预应力作用。以中跨跨中截面为例，拓宽拼接前后新旧桥主梁结构桥面板各点的挠度横向分布如图9所示。

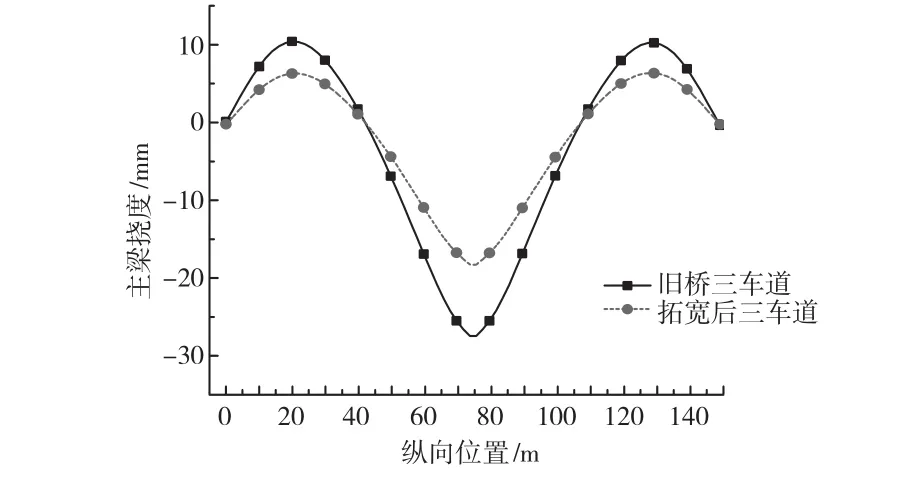
图8 活载作用下旧桥主梁挠度图

由图8可知, 在相同活载作用下，拓宽后整体箱梁的挠度相比拓宽前明显降低，旧桥中跨跨中截面箱梁顶板中心点的最大挠度为-27 mm，拓宽后该挠度减小到-18 mm，两者相比下降约33%，说明通过横向加劲肋的传力途径，使新建桥梁分担了相当一部分车辆荷载作用。另由图9可知，加劲肋拓宽拼接前、后旧箱梁顶板各点的竖向挠度在横桥向的分布规律基本相同，仅仅竖向挠度大幅度减小。这些事实都说明横向加劲肋可以有效地连接新旧箱梁，使得新旧箱梁具有较好的整体性。

图9 拓宽前后跨中截面变形变化图

（2）加劲肋应力分析

如图10所示，在旧桥侧偏载作用下，中跨跨中截面的旧桥侧加劲肋底部主拉应力达到了3.2MPa，处于开裂边缘。分析表明，加劲肋结构尺寸需进一步优化，需适当减小横向加劲肋结构刚度，以此降低横向拉应力值避免混凝土开裂。

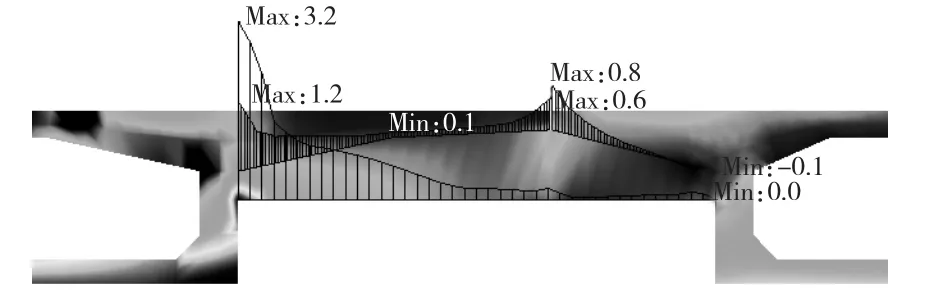
图10 中跨跨中截面加劲肋应力图（单位：MPa）

1.3 综合受力工况分析

通过上述分析可知，在各种荷载作用下加劲肋受力极值一般出现在角点。对上述已经完成的分析进行汇总，并适当考虑材料徐变效应对应力折减的作用，主要截面位置处加劲肋控制点的第一主拉应力参见表1。

由表1可知，对加劲肋受力影响最大的是支点截面基础沉降作用，其次是新旧桥材料收缩及徐变效应差影响，活载偏载作用对于跨中截面加劲肋的控制点应力影响较大。

在边支座截面，由于基础不均匀沉降导致的点4主拉应力较大，但考虑徐变作用所带来的应力折减效应，该应力折减系数取为0.45[19]，该项应力降低为2.59 MPa；收缩、徐变作用下各加劲肋的应力状态也超过了2 MPa，其中边支座截面点2处拉应力达到了2.85 MPa。

综上，各拉应力状态总和仍然较大，对结构的安全影响不容忽视，因此，该问题有待于进一步研究。可对横向加劲肋结构进行优化设计、采用抗拉性能好的钢纤维混凝土，以防止结构出现裂缝。

表1 加劲肋控制点处主拉应力表 MPa

2 拓宽后结构受力状态变化

上述分析仅针对横向加劲肋，本节将对拓宽后原有结构的内力变化状态进行分析讨论。

拓宽前后结构的内力借助梁格法模型来计算完成。原桥在拓宽拼接前后的结构形式、边界条件及其它各种作用的变化都会给原桥内力带来影响，现分析中主要考虑结构自重、预应力、收缩和徐变作用、温度梯度作用、基础不均匀沉降以及车辆活载等各项作用的综合影响。

为建立梁格法模型，盐河大桥横截面纵向梁格划分如图11所示。结构计算模型中，全桥共划分为1 813个单元。剪力-柔性梁格模型考虑了预应力钢筋的作用，材料参数均按照桥梁原有设计要求取值。

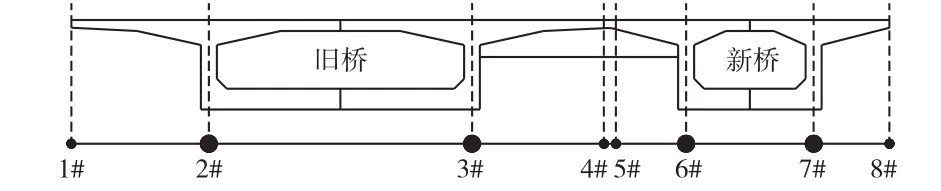
图11 盐河大桥拓宽箱梁横截面梁格划分示意图

梁格模型的支座约束条件按照实桥进行模拟，如图12所示。

图12 盐河大桥平面梁格划分示意图

计算分析当中，中纵梁和拼接加劲肋是主要控制构件，本文将主要分析上述构件的受力状况。主要控制截面有：1#边跨支点截面、2#边跨1/4截面、3#边跨跨中截面、4#边跨3/4截面、5#中支点截面、6#中跨1/4截面、7#中跨跨中截面，如图13所示。

图13 计算分析控制断面划分示意图

拓宽前后原桥主梁弯矩和剪力对比详见表2、表3 。

表2 拓宽前后原桥弯矩值 kN·m

表3 拓宽前后原桥剪力值 kN

上述计算成果表明，利用横向加劲肋群完成新旧箱梁横向拼接后，既有箱梁结构在各关键截面的内力有所变化。（1）截面弯矩:支点截面的负弯矩略有增加，增加幅度小于3.3%，不影响结构安全；各跨中截面的正弯矩都呈减小状态，如3#边跨跨中截面的弯矩减小12.06%。（2）剪力:支点位置剪力有所增加，如5#中支点截面剪力增加了10.98%，而其它截面的剪力变化很小。尽管如此，横向拓宽后5#中支点截面的剪力值仍小于该截面的抗剪承载力，结构仍是安全的。因此，利用横向加劲肋进行横向拼接后，原有箱梁结构各关键截面的抗弯和抗剪承载力仍符合设计要求，没有结构安全问题。

3 加劲肋参数分析

本节将研究加劲肋尺寸参数的变化对结构的影响，具体讨论加劲肋的高度、宽度和布置间距变化时新旧箱梁及加劲肋自身的受力变化情况，通过分析，可以得到如下结论：

（1）拼接加劲肋的构造尺寸对新旧箱梁受力变化影响较小，当拼接加劲肋构造尺寸变化时，新旧箱梁所受的最大、最小弯矩以及剪力的变化很小，变化幅度一般在5%上下，最大不超过10%。

（2）拼接加劲肋的构造尺寸对自身受力状态影响较大。选取图13中的7个控制截面，分析采用不同高度和厚度的加劲肋结构拓宽时，加劲肋自身的最大弯矩和最大剪力。图14为不同加劲肋高度的最大弯矩变化图，图15为最大剪力变化图，图16为不同加劲肋厚度最大弯矩变化图，图17为最大剪力变化图。

图14 不同加劲肋高度的最大弯矩变化

图15 不同加劲肋高度最大剪力变化

随着拼接加劲肋的高度和厚度的增大，拼接加劲肋受到的最大弯矩值和最大剪力值均明显增大，变化幅度较大，最大可达342%，最小也达到23.8%。当拼接加劲肋尺寸参数较小时，各拼接加劲肋所承受的最大弯矩值和剪力值相差不大，随着加劲肋高度和厚度的增加，支撑截面附近位置处加劲肋的最大弯矩值和最大剪力值明显增大，增幅最为明显。

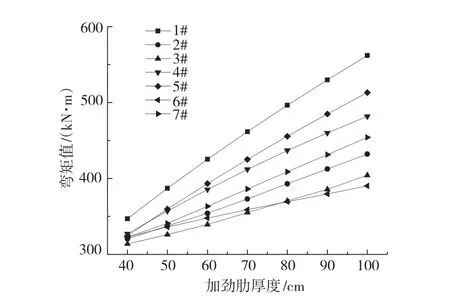
图16 不同加劲肋厚度最大弯矩变化

图17 不同加劲肋厚度最大剪力变化

（3）分析不同布置间距对加劲肋结构的影响，表4为不同布置间距对应加劲肋内力的数值表。表4中，最大弯矩是指承受最大弯矩的拼接加劲肋的弯矩值和对应剪力值，最大剪力同理；平均最大弯矩是指所有加劲肋在综合作用下所能承受最大弯矩值的平均值，平均最大剪力同理。从表4中可以看出，随着布置间距的增大，每根加劲肋所需承受的弯矩和剪力值也随之增大，即随着布置间距的增大及加劲肋数目的减少，每根加劲肋需要承担更大的内力。为了更好地查看加劲肋布置间距变化时内力极值的变化情况，以4 m基准“1”，分析结果如表5所示。

表4 不同布置间距对应加劲肋内力数值表

表5 不同布置间距对应加劲肋内力变化比值

由表5可知，随着布置间距的增大，加劲肋承担的弯矩值和剪力值也随之增大，每根加劲肋承担荷载的效率得到了提高。需要注意的是，设计中不能盲目增大布置间距，必须满足结构强度和变形的要求。

4 结论

本文基于有限元方法，研究分析了用于三向预应力混凝土连续箱梁桥横向拓宽结构中的横向加劲肋结构的静力受力特性，得到如下结论：

（1）在新旧箱梁结构的收缩、徐变变形差作用下，边支座截面的拼接加劲肋处于最不利受拉状态，尤其是横向拉应力较为明显，最大拉应力值达到了2.1MPa。加劲肋横向开裂可能性较大。

（2）新桥基础沉降作用下，新旧主梁存在明显的竖向变位差，致使新旧主梁拼接段处，新桥翼缘板或加劲肋底部以及旧桥翼缘顶部明显受拉，支座截面拉应力状态明显大于跨中其余截面，所以需重点关注各支座截面主拉应力状态；同时计算中考虑了混凝土应力松弛效应，沉降差造成的拼接结构拉应力仍然较大，因此仍需采取必要的结构加强措施来降低混凝土开裂的危害性，建议使用纤维混凝土等方法探讨有效解决拉应力过大问题。

（3）相比于拼接前旧桥箱梁来说，拓宽拼接后的结构整体刚度有明显提高，且能有效减小旧桥活载作用效应，说明横向加劲肋能够有效连接新旧箱梁，使得拓宽后结构共同受力和变形；拓宽后原有箱梁结构各关键截面内力有所变化，其抗弯和抗剪承载力仍符合设计要求，没有结构安全问题。

（4）加劲肋尺寸参数和布置间距的变化对新旧箱梁受力变化影响较小，对加劲肋自身的应力影响较大。尽管加劲肋自身仍然存在较大拉应力，需要进一步优化设计参数，但本文方法仍是一种可供选择的方案。

参考文献

[1]吴文清，叶见曙，鞠金荧，等.高速公路扩建中桥梁拓宽现状与方案分析[J].中外公路，2007，27（6）：100-104.

[2]吴文佑，吴文清，叶见曙.预应力混凝土桥梁拓宽的若干关键问题研究[J].公路交通科技（应用技术版），2009（8）：19-21.

[3]宗周红，夏樟华，陈宜言，等.既有桥梁拓宽改造纵向接缝研究现状与实例分析[J].福州大学学报，2009（2）：248-260.

[4]贺铁飞，孙铁钢.既有桥梁拓宽上部结构接缝处理方法分析研究[J].城市道桥与防洪，2012（6）：228-230.

[5]翟建勋.大悬臂混凝土箱梁桥横向拓宽拼接加劲肋的设计研究[D].南京：东南大学，2016.

[6]郝曙光.三向预应力连续箱梁桥拓宽的横向拼接构造设计与试验研究[D].南京:东南大学，2012.

[7]谢宝玉.银川黄河大桥拓宽的纵向缝设计[J].公路，2006（2）：19-23.

[8]吴文清，翟建勋，林晶.银川黄河大桥横向拓宽拼接构造使用状况调查研究[J].世界桥梁，2015（6）：83-87.

[9]Maadani S，Akbari R，Maalek S. Monitoring the dynamic characteristics of an urban bridge before，during and after widening[J]. Structure & Infrastructure Engineering，2015，11（7）：944-956.

[10]陈娣，刘斌.塘河大桥加宽改造技术方案研究[J].现代交通技术，2007，4（2）：52-55.

[11]王林，陈海卿.沪宁高速公路扩建工程塘河大桥拓宽施工[J].世界桥梁，2008（1）：22-24.

[12]方志，常红航，阳先全，等.混凝土箱梁桥拓宽拼接后收缩和徐变引起的横向效应[J].中国公路学报，2013， 26（6）：65-72.

[13]茹毅，刘其伟.收缩徐变作用下混凝土连续箱梁拼宽桥拼接段受力性能研究[J].中外公路，2016（2）：196-200.

[14]陈康明，吴庆雄，陈宝春，等.拓宽长联桥梁部分拼接方法与拼接构造试验[J].中国公路学报，2016，29（11）：99-107.

[15]刘桂红.长联空心板桥拼接方案研究[J].公路工程，2011，36（5）：40-43.

[16]吴文清，叶见曙，华斌，等.沪宁高速公路扩建桥梁拓宽关键技术研究[A].交通部公路科学研究院.全国既有桥梁加固、改造与评价学术会议论文集[C].北京：人民交通出版社，2008：120-129.

[17]Wollmann，G. P.，Anderson, R. B., & Roberts-Wollmann, C.L. Creep and shrinkage effects in spliced prestressed concrete girder bridges. PCI Journal，2003，48（6），92-105.

[18]韩重庆，冯健，吕志涛.大面积混凝土梁板结构温度应力分析的徐变应力折减系数法[J].工程力学，2003，20（1）：7-14.

[19]Bishara，A. G.，& Jang，S. Z.（1980）. Settlement-induced forces in concrete bridges. Journal of the Structural Division，106（7），1423-1436.

[20]温庆杰, 朱玉晓, 王东权. 箱梁桥横向拓宽后的基础沉降附加内力分析[J].中国矿业大学学报，2011，40（3）：351-356.

[21]Shi，X.，Li，X.，Ruan，X.，& Ying，T.（2008）. Analysis of structural behavior in widened concrete box girder bridges.Structural Engineering International，18（4），351-355.

[22]吴胜兴，周氐.大体积混凝土温度应力松弛系数的优化确定[J].河海大学学报(自然科学版)，1993（2）：47-53.