CEEMDAN结合LMS算法在轴承信号降噪中的应用
朱 敏,段志善,郭宝良,王 苗
(西安建筑科技大学机电工程学院,西安 710055)
滚动轴承是机械设备应用最广泛的部件之一,也是最易损坏的元件之一。所以对滚动轴承进行检测是非常必要的,提取滚动轴承的故障特征频率是诊断滚动轴承故障的关键[1-2]。轴承发生故障,故障信号大多数表现为非平稳的冲击脉冲信号,其宽度较窄[3],在实际测量当中,设备的工频以及背景噪声往往会淹没冲击信号。
经验模态分解(EMD)可以将原始信号分解为多个IMF分量,但是存在严重的模态混叠问题。完整经验模态分解(Complete Ensemble Empirical Mode Decomposition with adaptive noise,CEEMDAN)是EMD的改进算法,它在分解的每一阶段添加自适应的白噪声,消除模态混叠现象并且可以将重构误差降为最低。
基于EMD方法的降噪,关键是IMF的选择问题,IMF选择不当会导致降噪效果不佳或造成有用信号的丢失。文献[4]提出使用均方根误差与相关系数建立数学模型来选择有效的IMF分量重构信号来进行降噪。但是在有冲击信号的情况下,相关系数算得的值很小,方法就失去了效果。文献[5]在选择IMF分量中引入了排列熵的概念,当某一分量排列熵值大于0.6时,就舍去这一分量,这种方法很容易删去有效的信号。文献[6]计算各IMF分量相关函数与原信号自相关函数的相关系数,根据相关系数来选择合适的IMF分量,但是未给出相关系数的取值范围。
本文在IMF分量处理中引入了LMS(Least Mean Square)自适应滤波算法。这种方法是利用噪声信号与实际信号的均方误差最小,将噪声从实际信号中滤除。该方法能够自动地调节滤波器参数,以适应信号和噪声未知的或随机变化的统计特性,实现最优滤波[7]。
考虑到CEEMDAN与LMS算法的特点,提出一种CEEMDAN与LMS结合的方法。先将信号进行CEEMDAN分解,然后将分解所得的每个IMF分量对应使用LMS降噪,最后重构信号。本方法避免了取舍IMF分量所带来的误差,通过处理仿真与真实信号来验证方法的有效性。
1 EEMD与CEEMDAN
EMD是一种分析非线性和非平稳信号的自适应信号分解方法,其本质是将信号分解为具有不同频率的本征模态分量(IMF)。但当信号当中存在间断的跳跃变化时,将直接导致EMD分解产生不期望的模态混叠现象,导致分解结果失去实际意义[8]。现阶段研究EMD方法,主要还是集中在抑制模态混叠现象这一方面[9]。EEMD是基于EMD的一种解决模态混叠的算法;CEEMDAN是在EEMD的基础上发展的一种改进的算法。
1.1 EEMD
EEMD方法通过往原信号中多次添加不同的白噪声,分别进行EMD分解,然后对多次EMD分解所得的IMF进行平均而得到最终的实际分量,它能够有效改善EMD方法所产生的模态混叠现象,多次集成平均也起到了抵消白噪声影响的作用[10]。
EEMD算法的实现如下:
(1)令s(t)表示原始信号序列,vi(t)代表第i次实验中添加的具有标准正态分布的白噪声序列。第i次的信号序列表示为si(t)=s(t)+vi(t)其中i=1,…,I表示实验次数。
(2)将每一次实验产生的信号序列si(t)进行EMD分解,得到,其中k=1,…,K,表示分解的IMF模态个数。
(3)定义s(t)的第k个模态分量为IMFk,相应地对进行平均得到
1.2 CEEMDAN
EEMD所添加的白噪声序列通过有限次平均后,并未完全抵消,重构误差的大小依赖于集成的次数,虽然随着平均次数的增多可以逐渐减小,但很大程度上又增加了计算耗时。
CEEMDAN方法通过在每个阶段添加有限次的自适应白噪声,能实现在较少的平均次数下,其重构误差几乎为0。因此,CEEMDAN可以克服EMD所存在的模态混叠现象,同时解决了EEMD分解的不完整性以及依靠增大集成次数来降低重构误差而导致的计算效率低的问题[11-12]。
在EEMD分解中,包含不同白噪声的si(t)在每一次实验中均进行不同的分解。因此,每一次分解产生的余量信号均不同,即
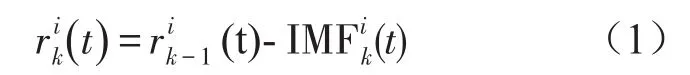
在EEMD基础上,Ceemdan通过添加自适应的白噪声以及计算唯一的余量信号获取IMF分量,以克服EEMD的不足,使得信号重构后与原信号几乎完全相同。
定义算子Ek(∙)为通过EMD方法所产生的第k个模态分量,CEEMDAN所产生第k个模态分量记为,CEEMDAN具体的算法实现如下:
(1)与EEMD分解方法相同,CEEMDAN针对信号s(t)+vi(t)进行I次实验,通过EMD方法分解以获取第1个模态分量,计算
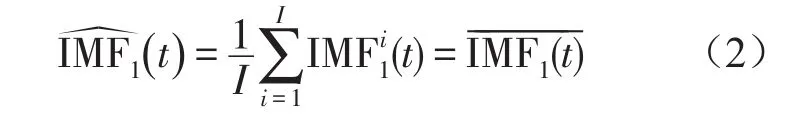
(2)在第1阶段(k=1),计算第一个唯一的余量信号,即计算
(3)进行i次实验(i=1,…,I),每次实验中,对信号进行分解,直到得到第1个EMD模态分量为止。在此基础上,计算第2个模态分量如下

(4)对其余每个阶段,即k=2,…,K,计算第k个余量信号,与步骤(3)的计算过程一致,计算第k+1个模态分量如下
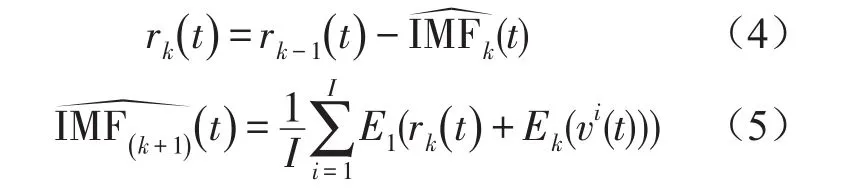
(5)执行步骤(4),直至所获取的余量信号不再能进行分解为止,其判断标准为余量信号的极值点个数至多不超过两个。
算法终止时,所有模态分量的数量为K。最终的余量信号为
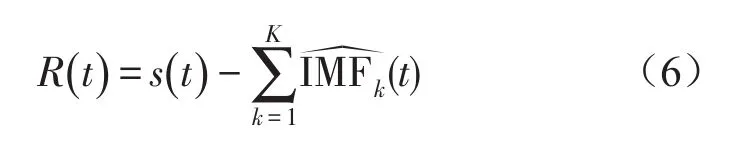
因此,原始信号序列s(n)最终被分解为
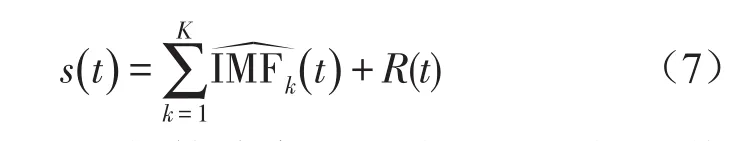
从CEEMDAN的算法实现及式(7)可看出,其分解过程是完整的,能对原始信号进行精确重构。该方法既能实现EEMD解决模态混叠的功能,通过添加不同的白噪声,也能够使重构误差减小。
2 LMS方法
LMS算法性能稳定、结构简单且易于实现,应用广泛,它的基本原理是将被噪声污染的信号与参考信号进行抵消运算,从而消除带噪声信号中的噪声[13]。关键是自适应噪声抵消系统的参数信号需要与待消除的噪声具有一定的相关性,而与检测或提取的信号不相关[14]。
图1中表示自适应噪声消除系统的原理图。系统的输入分两路,一路为有用信号s混有噪声,一路为消噪系统中自适应滤波器的参考输入(噪声n2),噪声n1和n2存在相关性,属于同一类型零均值平稳随机过程,噪声与有用信号s之间相关性较小,则系统的输出等于误差信号

其中:n′为噪声n2通过自适应滤波器的估计。
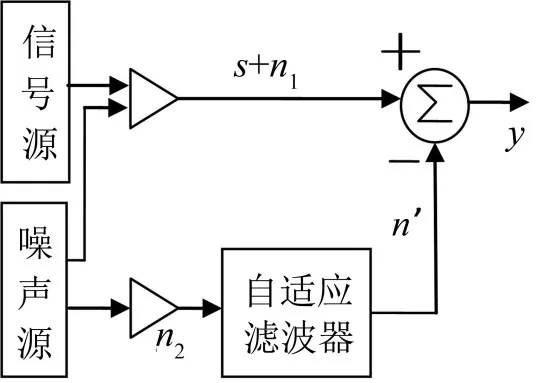
图1 自适应滤波器消噪原理
自适应消噪原理为:以输出信号的均方值作为评价指标,希望系统经过自适应算法使噪声全部被抵消,只剩下有用信号,即当自适应滤波器得到最优估计时,输出信号y就是对原始有效信号的最好估计。
假设系统测试k时刻滤波器加权矢量为W(k),M为滤波器长度或阶数,则均方误差的期望计算为
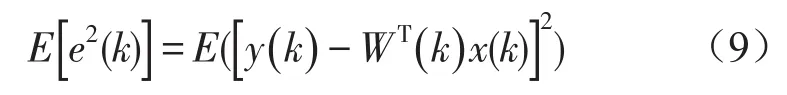
其中:x(k)为输入原始带噪信号矢量。
基于最小均方LMS算法,以稳态均方误差每次迭代的瞬时平方值替代其均方值,并以此来估计滤波器系数的梯度方向,滤波器估计的方法为

其中:μ为步长因子,其取值范围为1<μ<1/λmax,λmax是输入信号自相关矩阵的最大特征值。
3 评价准则
为了便于检验降噪方法的信号处理效果,使用均方根误差、信噪比作为评价标准
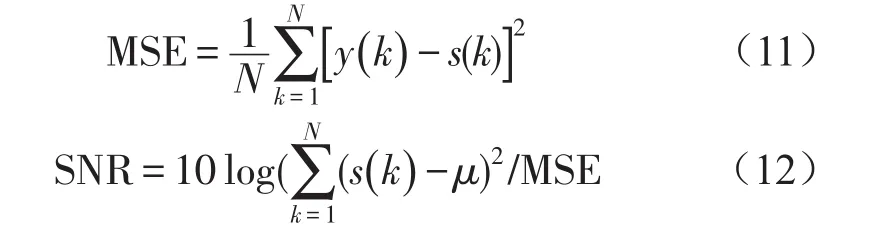
均方根误差是一个总体精度的衡量指标,MSE越小,说明重构信号与原始纯信号的逼近程度越好;信噪比为有效信号与干扰信号的比较,可以评价方法的去噪效果。
4 CEEMDAN结合LMS方法
LMS算法适用于频率单一的情况。考虑1种方法,就是可以将复杂的多频信号,分解为适合LMS处理的单频信号。CEEMDAN即能够解决EMD方法的频率混淆问题,也降低了EEMD计算后重构的误差。其分解得到信号的单频IMF分量,然后通过自适应算法对每1个IMF进行降噪处理。
下图2是CEEMDAN结合LMS算法的流程图。
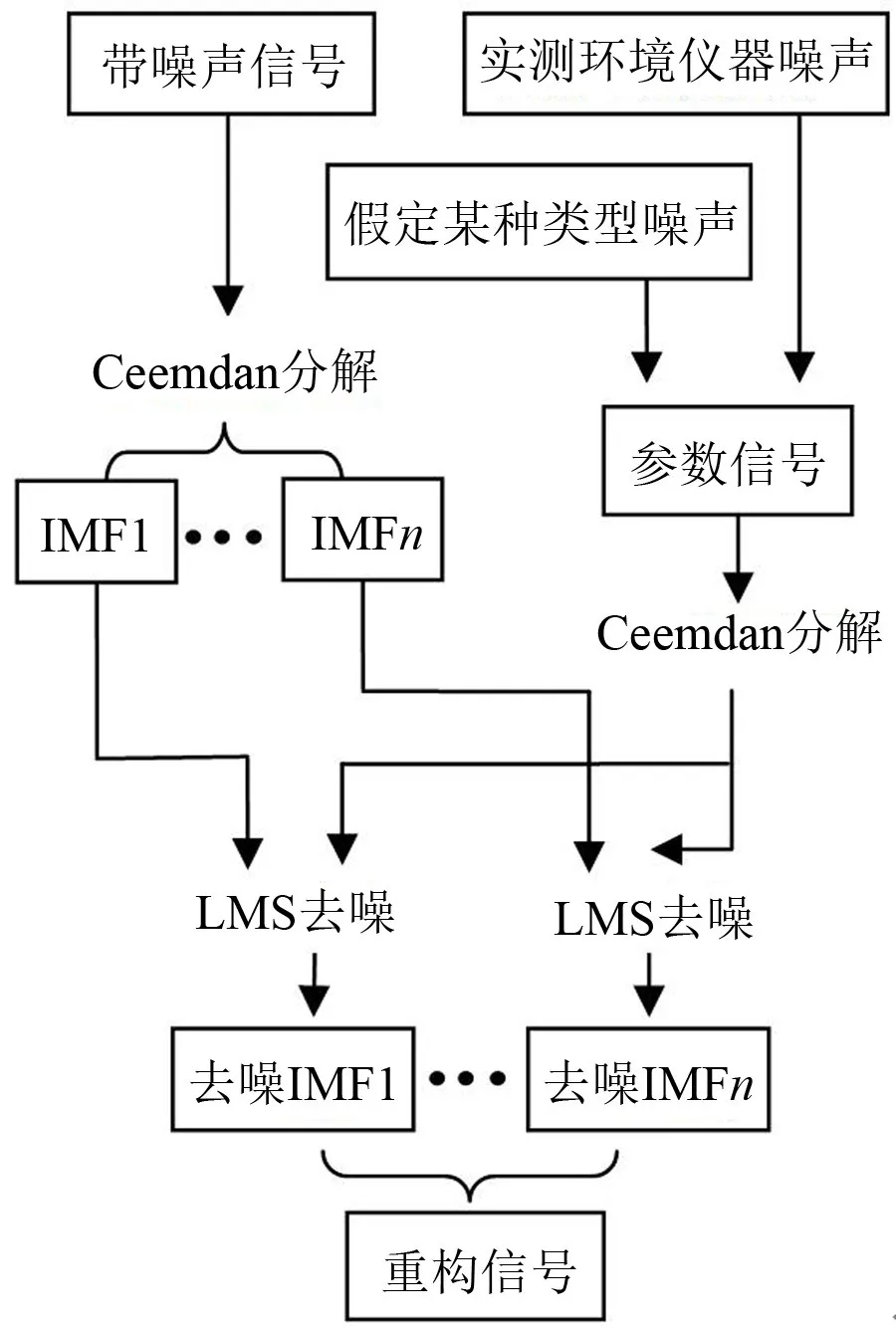
图2 CEENDAN结合LMS降噪流程
下面是新方法的具体步骤:
(1)将采集到的原始带噪声信号进行CEEMDAN分解,分解为多个IMF分量。
(2)将实际测量到的噪声信号同样也进行CEEMDAN分解,分解为多个IMF分量。如果环境噪声很难测到,可以使用某种仿真噪声代替。
(3)两次分解所得到分量一一对应,噪声分量作为参考分量,使用LMS算法对原始信号分量进行滤波处理得到去噪的IMF分量。由于CEEMDAN加入白噪声的作用,分解的频率以相同的频率下降[15]。
(4)最后,把去噪的IMF分量相加,得到了降噪后的信号。
5 新方法的仿真信号分析
设计1组仿真信号,这组信号是由有效信号与噪声信号组成。将噪声信号设置成与仿真信号频率相接近的信号,在振动筛信号分析中,针对物料与筛面冲击的作用,噪声信号还包括白噪声信号。
有效信号为

设置3组噪声信号分别是
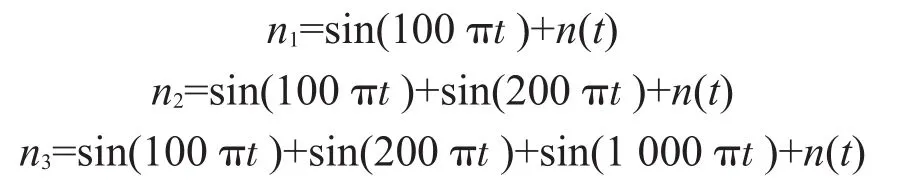
其中:n(t)为均值为0、方差为1的高斯白噪声。为了计算方便设置采样频率为fs=1 000 Hz,采样点个数为N=2 000。
以加入第1种噪声为例,将其合成信号(记作s1)进行降噪处理。先将信号进行CEEMDAN分解,分解得到11个IMF分量。同样将噪声n1也进行CEEMDAN分解,得到的分量对应作为每1组IMF分量的参考信号。每组IMF使用LMS滤波,滤除噪声信号。将滤波后的11组IMF组合形成新的信号,即降噪后的信号,记作s11。
图3与图4为降噪前后信号的时、频域图,由时域图对比可以看出经过降噪后的信号,噪声明显减少,可以清晰看出信号的波形;由频域图对比可以看到,白噪声信号产生的频率几乎被完全抑制,频率为50 Hz的正弦信号幅值由1.05减少为0.43。由此可以得出新方法对于信号降噪具有明显的效果。

图3 降噪前时、频域图
下面用另外两组噪声信号与有效信号组合,用均方根误差、信噪比比较降噪效果。
由表1、表2可以看出新方法对于平稳信号具有良好的降噪效果,设定相同的步长M、阶数μ,随着噪声信号的叠加个数增加,降噪前后的均方根误差将会增大。
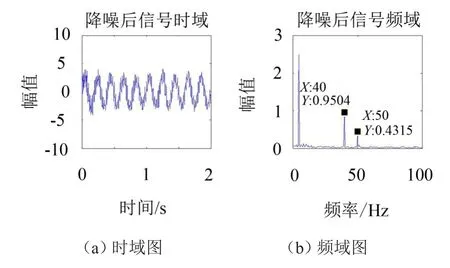
图4 降噪后时、频域图

表1 降噪前信噪比

表2 降噪处理后信噪比与均方根误差
做进一步研究,加大噪声,使原始有效信号与噪声信号的信噪比较降低。调整LMS算法中步长与阶数的值,通过对信号的处理,可以发现在信噪比大于-25 dB时,新方法对数据处理有明显效果;但在低于-25 dB时,信号中的有效成分基本被滤除。下图为添加噪声达到-25 dB时的去噪效果图,经过新方法去噪后信噪比由-25 dB提高到了-9.5 dB。
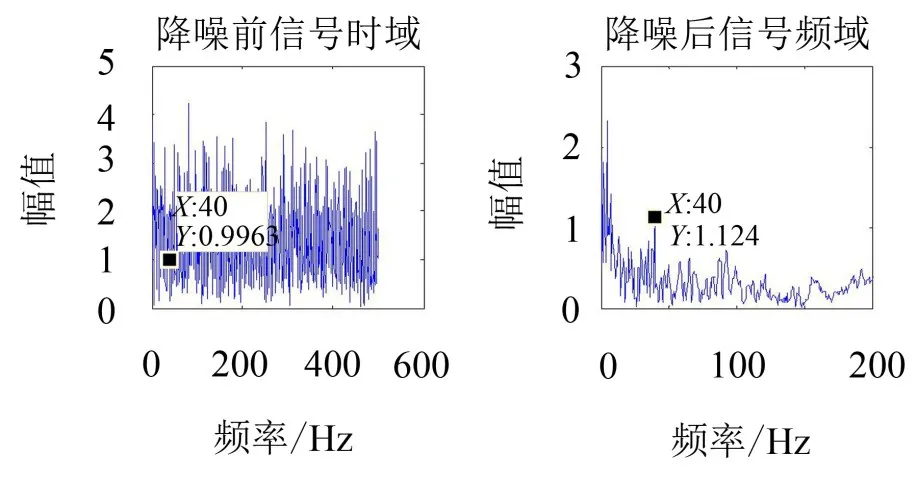
图5 信噪比为-25 dB时的降噪效果
所以此方法适用于包含噪声个数较少且信噪比大于-25 dB的情况下。
以上分析均为对平稳信号分析,在轴承的故障诊断中,轴承故障中90%是由内外圈故障引起[16],具有非平稳的特点。下面用非平稳信号进行分析。
采用有效信号为s=10e-10tsin(20πt),该冲击信号的频率设置为50Hz。噪声信号为n=sin(40πt)+n(t),n(t)为高斯白噪声。
图6(a)所示为原始有效信号,图 6(b)、图 6(c)为降噪前后的信号时域图,可以看出降噪前信号脉冲峰值大部分都被噪声淹没,降噪之后有效信号峰值变得明显。图6(d)、图6(e)为降噪前后频谱图,图6(d)中含有明显的噪声,经过新方法降噪后,工频成份与噪声含量明显较少,频率50 Hz及其倍频100 Hz、150 Hz,可以被清晰找到。
将降噪前后的信噪比列出表3,可以发现该方法提高了信噪比。
由以上分析可以得到,新方法不仅适用于平稳信号,也同样适用于非平稳信号,且降噪效果明显。

表3 非平稳信号降噪分析
6 新方法的实验信号处理
对振动筛轴承故障进行分析。实验研究对象为如图7所示的振动筛,使用传感器采集轴承振动的加速度信号。对信号先进行滤波处理,滤除不必要的高频成分。
振动筛在工作过程中往往会含有噪声信号,工作条件比较恶劣,使得信号中的故障信号很小,基于新方法对振动筛故障信号进行分析,参考信号来源于轴承正常工况下所测量得到的振动信号,同样也对参考信号滤波,滤除高频成分。
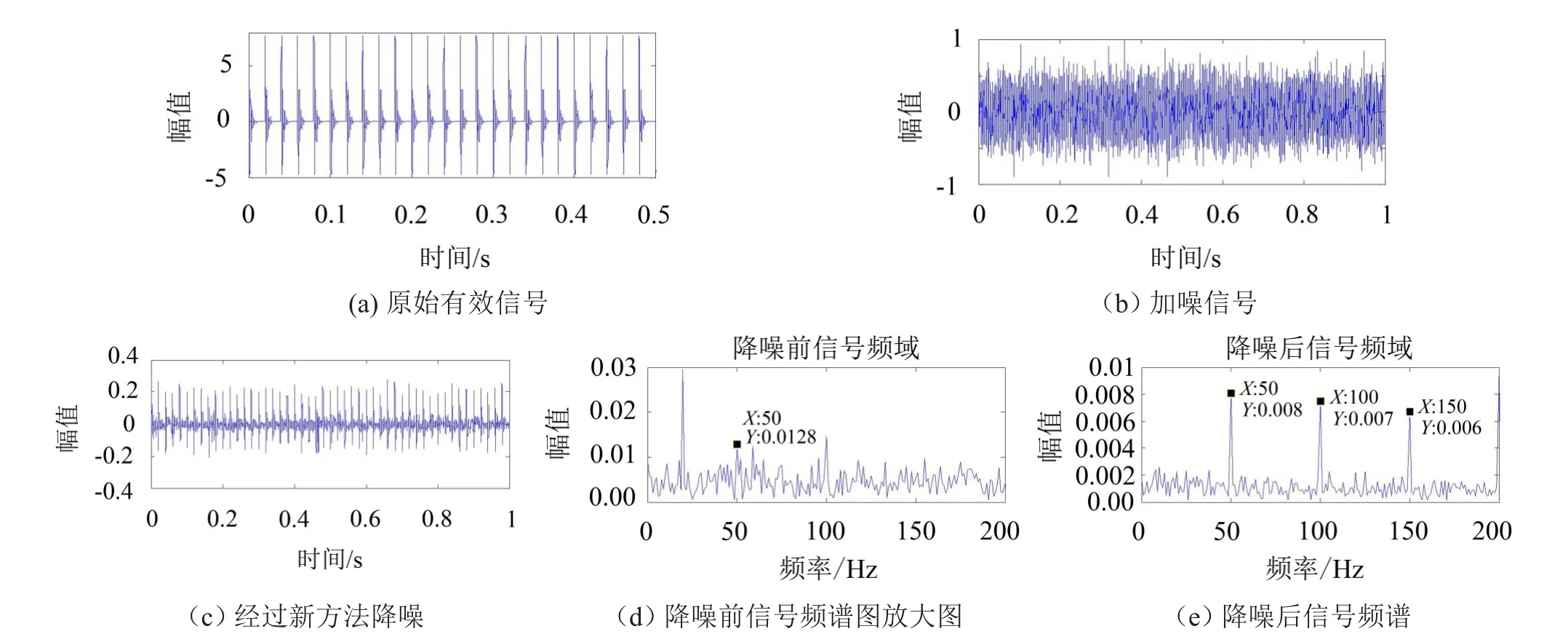
图6 非平稳信号降噪效果

图7 实验用到的振动筛及其轴承
图7为实验所用到的振动筛以及在该振动筛上使用的轴承。
在采集信号之前先要测量计算振动筛轴承的各个参数,轴承的各个参数如表4所示。
振动筛的工频fs为16.7 Hz,通过下列公式计算可得,外环故障特征频率fe为104.2 Hz,内环故障特征频率fi为145.9 Hz。
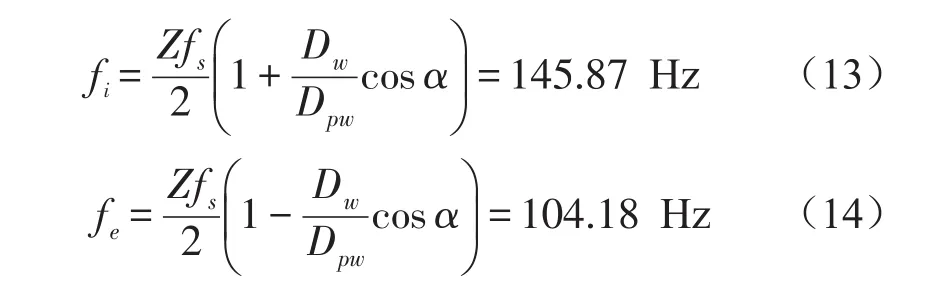
用上述新方法对实验所测信号数据进行处理得到的结果对比见图8。
图8(a)、图8(b)为原始信号与降噪后的时域图,对比可以看出信号中大部分噪声成份被滤除。图8(c)、图8(d)为降噪前信号频谱及其放大图,图8(e)为采用新方法降噪后的信号频谱图。图8(d)图中,原始信号的频谱噪声成分很多,无法找到有效的频率;图8(e)图中,工频信号被完全消除,噪声干扰减少,可以很清晰地找出104 Hz以及它的倍频成份。
分析这组数据得出结论:振动筛滚动轴承外环发生故障。通过仿真信号与实验信号分析,基于CEEMDAN结合LMS算法能够有效降低信号中噪声的含量,凸显冲击成分,并能够应用在振动筛轴承故障诊断中。

表4 轴承参数
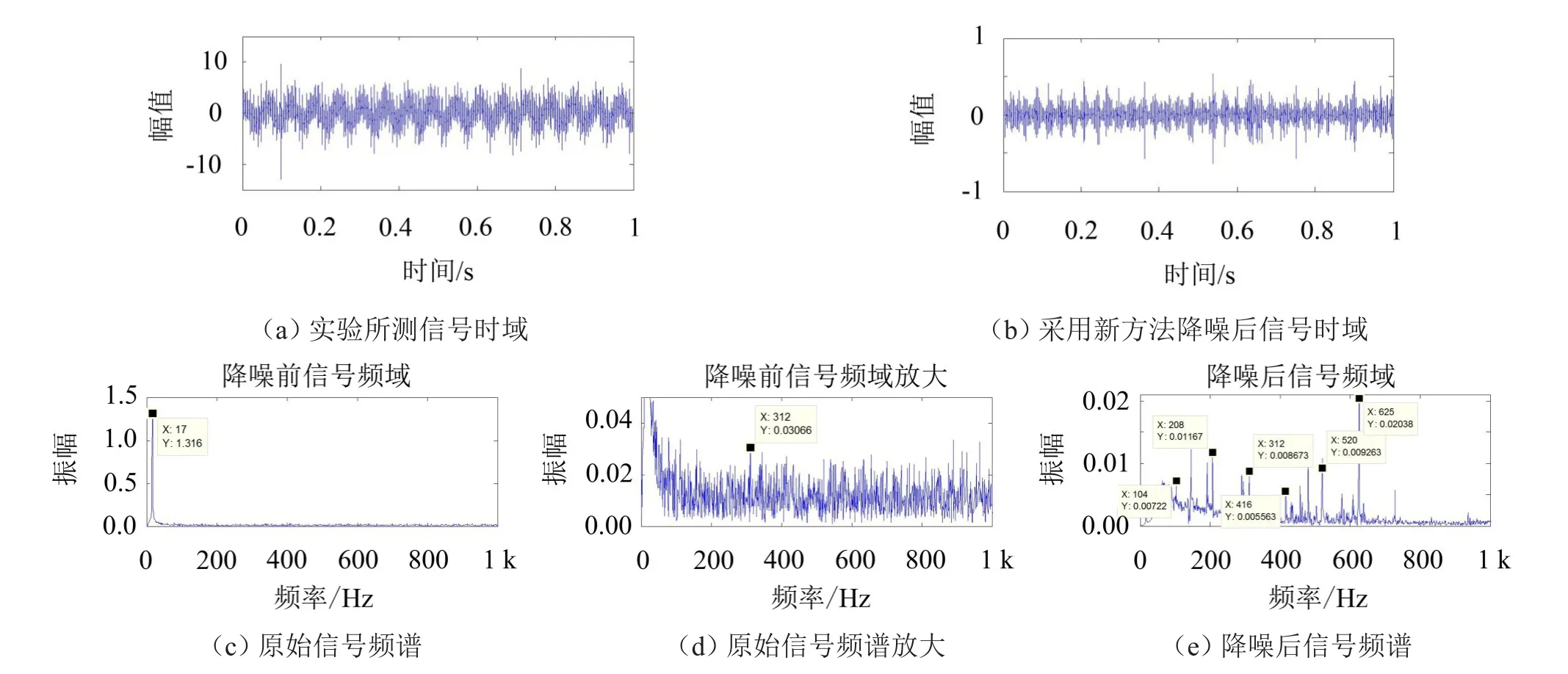
图8 试验信号降噪效果
7 结语
(1)基于CEEMDAN的信号提取方法,虽然适合于非线性、非平稳信号,但其分析过程中并不能将噪声干扰排除在外,而LMS算法的自适应滤波可以将有效信号与噪声信号分离,起到了很好的降噪作用。
(2)提出了CEEMDAN结合LMS的信号处理方法,该方法不仅适用于平稳信号,而且也适用于非平稳信号,可以有效提高信噪比。
(3)新方法可以应用在轴承故障诊断中。适用范围为信号信噪比高于-25 dB的情况,且噪声所含个数越少,降噪后的重构误差越小。
参考文献:
[1]姜战伟,郑近德,潘海洋,等.基于改进多尺度熵与VPMCD的滚动轴承故障诊断[J].噪声振动与控制,2017,37(3):156-161.
[2]高强,杜小山,范虹,等.滚动轴承故障的EMD诊断方法研究[J]. 振动工程学报,2007,20(1):15-18.
[3]孙晖,朱善安.基于自适应滤波的滚动轴承故障诊断研究[J]. 浙江大学学报,2005,39(11):1746-1787.
[4]郑一,孙晓峰,陈健,等.基于集合经验模态的随钻脉冲信号优良降噪算法[J].石油勘探与开发,2012,39(6):750-753.
[5]郑近德,程军圣,杨宇.改进的EEMD算法及其应用研究[J]. 振动与冲击,2013,32(21):21-46.
[6]陈任祥,汤宝平,吕中亮.基于相关系数的EEMD转子振动信号降噪方法[J]. 振动、测试与诊断,2012,32(4):543-546.
[7]宋知用.Matlab在语音信号分析与合成中的应用[M].北京:北京航空航天大学出版社,2016:176-181.
[8]张袁元,辛江慧.EMD方法的改进研究及其在机械信号中的应用[J].机械设计与制造,2016,(2):98-102.
[9]王婷.EMD算法研究及其在信号去噪中的应用[D].哈尔滨工程大学,2010.
[10]李军,李青.基于CEEMDAN-排列熵和泄漏积分ESN的中期电力负荷预测研究[J].电机与控制学报,2015,19(8):70-80.
[11]陈仁祥,汤宝平,马婧华,等.基于EEMD的振动信号自适应降噪方法[J]. 振动与冲击,2012,31(15):82-86.
[12]李锋,林阳阳.基于Ceemdan-SVM的液压泵故障诊断方法研究[J]. 液压与气动,2016(1):125-129.
[13]张袁元,李舜酩,胡伊贤,等.LMS方法的改进及联合EEMD在振动信号去噪中的应用[J].振动与冲击,2013,32(20):61-66.
[14]曹亚丽.自适应滤波器中LMS算法的应用[J].仪器与仪表学报,2005,26(8):452-455.
[15]FLANDRIN P,RILLING C,CONCALVES P.Empirical mode decomposition as a filter bank[J].IEEE Signal Processing Letters,2004,11(2):112-114.
[16]RUBINI R,MENEGHETTI U.Application of the envelope and wavelettransform analyses for the diagnosis of incipientfaults in ballbearings[J].Mechanical Systems and Signal Processing,2001,15(2):287-302.

