我国用电量的多元回归分析

申玉伟 曹晓祎

摘要

20世纪80年代以来我国用电量快速增长，为了研究我国用电量的影响因素，本文收集1995年2014年的电力消费量相关数据，并对其建立多元线性回归模型，对回归模型进行检验，合理预测我国电力需求量。

【关键词】用电量 多元回归 模型检验

1引言

电力工业己成为我国国民经济发展的基础产业。改革开放以来，我国的电力消耗量也保持快速增长。本文主要研究影响我国用电力量的因素，并建立预测我国用电量的多元回归模型。

2模型介绍

2.1模型基本假设

构建模型的基本假设如下：

（1）解释变量是确定性变量;

（2）随机误差项具有0均值和等方差;

（3）正态分布的假定条件为s～n（o，δ2），i=l，2，3，…;ε1，ε2，ε3，…相互独立。

2. 2模型的建立

多元線性回归模型记为：

Y=Xβ+ε

式中，因变量Y为n维向量;自变量x为n×p阶矩阵;误差项ε为n维向量。这意味着一共有n个观测值，有一个由向量Y代表的因变量及由X代表的p个自变量。

2.3模型的检验

在多元线性回归的标准输出中，对系数的t检验和方差分析的F检验是必不可少的。方程的显著性检验（F检验），旨在对模型中因变量与自变量之间的线性关系在总体上是否显著成立作出推断。方程的总体线性关系显著并不等同于每个自变量都对因变量的影响都显著，因此，必须对每个自变量进行显著性检验，以决定是否作为自变量被保留在模型中。这一检验是由对变量的t检验完成的。

3数据分析

3.1选取指标和收集数据

本文收集了1995-2014年共20年的相关数据，共选取9个指标。包括因变量y：每年电力消费量（亿千瓦小时）;自变量（Xl-XS）人口自然增长率（%。）、国内生产总值（亿元）、第一产业产值（亿元）、工业产值（亿元）、建筑业产值（亿元）、第三产业产值（亿元）、人均国内生产总值（元）、能源消费总量（万吨标准煤）。

3.2变量相关分析

用R软件进行相关性数据分析，找出影响我国用电量的主要因素。因变量y与自变量xl，x2，X3，X4，x5，x6，X7，xs的相关系数分别为-0.7798、0.9941、0.9905、0.9967、0.9846、0.9905、0.9946、0.9866，用电量与各个自变量之间关系很密切，可以认为存在线性相关关系。

3.3多元线性回归模型的建立与检验

由变量相关分析可知所选取的指标都与电力消费量存在线性关系，利用R软件对各指标数据建立多元回归模型，得出回归方程：y= -791.56081-137.10546x1-18.50722x2+1 8.15517x3 +18.11310 X4+17.96437x5 +18.41074x6 +3.51930x7+0 08423X8

在方差分析结果中，模型的F值为238，p<0.05，说明此模型有意义。t检验结果中偏回归系数b2，b3，b4，b5，b6，b8的p值都小于0.01，可认为解释变量X2， X3，X4，x5，X6，xs显著;Xl，X7的p值大于0.4，不能否定对β1=0，β7=0的假设，可认为xl，x7对y没有显著的影响。然而xl和x2所对应的偏回归系数都为负，这与经济现实是不相符的。出现这种结果的原因可能是这些解释变量之间存在高度的共线性。由数据散点图可知，x1与y的关系，可能是最偏离线性的。

3.4模型优化

3.4.1变量选择与模型建立

选用逐步回归法对变量进行选择。最终选择的变量为：x2，x3，X4 X5， X6和x8。对其进行多元线性回归分析。从方差分析表中，由F统计量的值可知回归方程是有意义的，且p<0.05，所以回归模型是有意义的。

3.4.2模型检验

优化后的多元线性回归方程为：

y= 388.20142 -17.85936x2 +17.69274x3+17.7932X4+17.39365Xs +18.00755x6+ 0.08218x8

由t检验结果可知，b2， b3， b4，b5，b6，b8的p值均小于0.05，所以这6个偏回归系数是有意义的，因此方程的各个系数也是具有统计意义的。

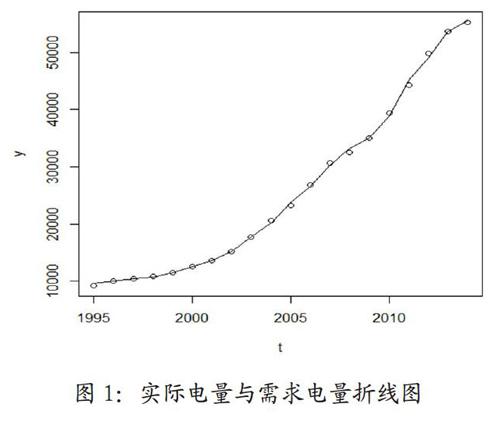
而且根据该线性回归模型计算所得出的电力需求量和实际电力消费量作出的折线图（图1），可以看到拟合效果不错。同时，标准残差和杠杆值图（图2）中绝大部分位于-2与2之间，并且关于0随机波动。

4结论

从本文所建的多元回归模型来看，能源结构持续优化调整，能源消费总量，国内生产总值，能效水平持续提高是影响我国电力消费量的主要因素。由参数估计结果可知，该模型在统计与经济意义上的可信度较强，同时回归模型拟合优度较好，能较好的预测未来我国电力消耗量。

参考文献

[1]徐丽娜.中国用电量需求模型的建立及需求预测[J].山西大同大学学报，2 01 3，2 9 （01）：18-19.

[2]王斌会.多元统计分析及R语言建模[M].暨南大学出版社，2016： 68-80.