具桩靴自升式钻井船插桩过程有限元模拟研究

安永宁

(1.交通运输部天津水运工程科学研究所，天津 300456；2.天津市水运工程测绘技术重点实验室，天津 300456)

自升式钻井船在海洋石油领域用途广泛，多用于钻井、修井，有时也被改造后用于采油作业中。自升式钻井船依靠3～4根桩腿插入海底面以下一定深度的持力层，获得承载力支撑上部荷载[1]。目前，许多自升式钻井船都在桩腿端部装有桩靴装置，桩靴一般为纺锤形或锥形，截面呈正多边形或圆形，截面最大尺寸在6～12 m范围。

桩靴的应用，提高了自升式钻井船插桩就位时的作业效率，增强了其在深厚软土海区的适用性，基础的自稳性也得到进一步增强。另外，较浅的插桩深度，一方面充分利用了浅部承载力，另一方面使得拔桩不再困难，易用性和安全性都显著提高。

新结构的应用需要相应理论方法的更新完善。在评价具桩靴自升式钻井船的插桩深度时，工程技术人员对于插桩作业中地基土的破坏机理、荷载影响深度等的认识并不明晰，在承载力计算时，有时将桩靴视作浅基础考虑，有时又视作桩基础考虑，这种疑惑甚至在具桩靴自升式钻井船的使用手册中都有反映[2-3]。

本文基于基础的极限破坏理论，应用有限元数值模拟手段，研究了具桩靴自升式钻井船插桩作用于均质地基土时，地基土的破坏模式和插桩荷载影响深度，以及不同承载力计算公式的适用性，解决了具桩靴自升式钻井船在实际应用中的工程技术疑难。

1 自升式钻井船承载力计算现状

目前，对具桩靴自升式钻井船的地基承载力及插桩深度进行评价时，常见的方法有两种，一种是以Skempton公式[4]、Terzaghi公式[5]、SNAME[6]规范等推荐的浅基础计算方法，另一种是以API RP2A[7]等规范推荐的桩基础承载力计算方法。

1.1 均质土浅基础承载力计算方法

(1)均质砂土。Terzaghi在假定条形基础且基础底面粗糙、地基处于整体剪切破坏、滑动范围内土体处于塑性平衡情况下，根据弹性楔形体的平衡条件得出了极限承载力计算公式

Pu=0.5γBNγ+γDNq+cNc

(1)

通常桩靴贯入地层属于圆形或方形基础作用，此时，若地基土发生局部剪切破坏，太沙基建议的相应修正公式如下

Pu=0.3γBNγ+γDNq+0.8cNc

(2)

以上公式中，c为地基土的黏聚力，γ为地基土的有效重度，B、D分别为基础的宽度(直径)和埋深，Nγ、Nq、Nc均为与内摩擦角相关的承载力系数，可查表求得。

(2)均质饱和软黏土。Skempton研究了饱和软黏土地基的极限承载力计算，解决了Terzaghi公式在φ=0条件下难以应用的问题

(3)

式中：Cu为基础底面以下0.707B深度范围内的地基土不排水抗剪强度；L为基础的长度，对于大部分桩靴，L=B；承载力系数Nc取5.14。

以上公式是基于均质地基土、破坏面已知、条形基础埋深固定不变等假定条件下，依据静力学平衡关系建立起来的，而海上自升式钻井船的桩靴基础一般为圆形或方形，地基土成层且非均质，插桩过程是不断贯入和破坏地基土的动态连续过程，很难满足公式的假定使用条件，因此，从理论上来说，将其用于计算桩靴承载力时不够精确。

1.2 SNAME规范桩靴承载力计算方法

美国造船与轮机工程师学会(the Society of Naval Architects & Marine Engineers, SNAME)发布的RecommendedPracticeforSiteSpecificAssessmentofMobileJack-upUnits中，给出了具桩靴钻井船插桩承载力的计算公式。

(1)在不排水饱和黏土中，不考虑回淤影响时，地基土可承担的桩靴极限竖向荷载按下式计算

(4)

式中：形状系数sc=1+(Nq/Nc)(B/L)，对于饱和黏土，通常Nq=1、Nc=5.14；深度修正系数dc=1+0.4(D/B)；A为桩靴最大横截面积；p0′为上覆的最大有效压力。

(2)在硅质砂或其他粒状土中，不考虑回淤影响时，地基土可承担的桩靴极限竖向荷载按下式计算

(5)

式中：γ′为地基土的水下有效重度；形状系数sγ=1-0.4(B/L)，sq=1+(B/L)tanφ；深度修正系数dγ=1，dq=1+2tanφ(1-sinφ)2f，当D/B≤1时，f=D/B，否则f=arctan(D/B)。

(3)在上软下硬层状土中，上层黏土会发生挤压，不考虑回淤影响时，地基土可承担的桩靴极限竖向荷载按Meyerhof给出的公式计算

FV=[(5+0.33B/T+1.2D/B)Cu+p0′]A

(6)

式中：T为软土层中桩靴最大截面至下伏硬土层的厚度。

(4)在上硬下软层状土中，桩靴可能会发生冲切，当上部硬土层为硬黏土时，如不考虑回淤影响，地基土可承担的桩靴极限竖向荷载按Brown给出的公式计算

(7)

式中：H为硬土层中桩靴最大截面至下伏软土层的厚度；Cu,t为上部硬土层的不排水抗剪强度，Cu,b为下部软土层的不排水抗剪强度。

当上部硬土层为砂土时，如不考虑回淤影响，地基土可承担的桩靴极限竖向荷载按下式计算

(8)

式中：FV,b为假定插桩在下伏软土层顶面且无回淤时的极限竖向荷载；Ks为冲剪系数，Kstanφ=3Cu/Bγ′。

SNAME方法在计算成层土的承载力时，假定桩靴预先插入一定的土层，没有考虑插桩过程对土层分布的影响以及不同的破坏机制，当上覆砂土层下伏软黏土层时，没有考虑到上覆砂土层的强度性质，只给出了下限解，因而得到的结果也不够精确[8]。

1.3 API桩基础承载力计算方法

美国石油学会(American Petroleum Institute, API)发布的Planning,DesigningandConstructingFixedOffshorePlatforms-WorkingStressDesign(API RP2A-WSD)中，给出了海上桩基础的单桩极限承载力计算方法，主要由极限桩端阻力和极限侧摩阻力两部分组成，在黏土和非黏土有着不同的计算方法。

(1)在不排水黏土中时，单桩极限承载力按下式计算。

Qd=Qf+Qp=fAs+qAp=αCuAs+9CuAp

(9)

(2)在非黏土中，单桩极限承载力按下式计算。

(10)

以上式中，f为单位桩侧阻力，As为桩侧总面积，q为单位桩端阻力，Ap为桩端总面积；α为不大于1的系数；Cu为计算点的不排水抗剪强度；K为横向压力系数，一般取1.0；δ为土与桩壁之间的摩擦角，Nq为与δ有关的支撑系数。

以上公式在计算无桩靴桩基础时，适用性较好。但当具桩靴钻井船插桩时，桩靴巨大的扩底效应完全扰动了桩侧地层，导致插桩产生的侧摩阻力很小，此外桩靴本身排出了相当大体积的土体，失去的这部分土体自重应增加到最终承载力计算结果中。因此，将API RP2A-WSD规范公式进行如下修正，更符合具桩靴钻井船插桩的力学作用原理

Qd=Qp+γV

(11)

上式也是一部分自升式钻井船操作手册中给出的推荐计算方法，其中V是桩靴排开土的体积。

API方法推荐的公式属于桩基础公式，但具桩靴的自升式钻井船插桩深度往往在5 m以内，或插桩深度小于桩靴尺寸，更符合浅基础的判断条件，API公式的应用效果如何尚需实际检验。

2 有限元数值模型建立

有限元法是一种求解偏微分方程边值问题近似解的数值技术。岩土材料有着非线性、各向异性等力学性质，大多数岩土问题非常复杂，通常难以得到准确解，而有限元法计算精度高，能适应复杂形状，在处理岩土工程问题中有着明显的优势[9-10]，一些学者利用有限元技术模拟了海洋工程插桩活动，取得了新的认识和符合实际的结果[11-19]。

本文拟采用有限元法，建立桩靴结构与海洋土体相互作用的有限元数值模型，对插桩活动进行数值模拟，通过将模拟结果与公式计算结果、插桩实例结果对比，来揭示具桩靴平台插桩时的地基土破坏方式，以及不同条件下的承载力计算方法。

2.1 单元及本构模型

桩靴单元为完全积分的线性实体单元，材料选用各向同性弹性材料，材料参数包括密度、弹性模量、泊松比。

土体单元为完全积分的线性实体含孔隙流体单元，材料选用各向同性弹塑性材料，其中，不排水黏土的本构模型为Mohr-Coulomb模型，材料参数包括密度、弹性模量、泊松比、内摩擦角(Friction angle)、剪胀角(Dilation angle)、黏聚力(Cohesion yield stress)、塑性应变(Abs plastic strain)、偏心率(Deviatoric/Meridional eccentricity)；排水无黏土的本构模型为修正的Drucker-Prager/Cap模型，材料参数包括密度、弹性模量、泊松比、p-t平面黏聚力(Material cohesion)、p-t平面摩擦角(Angle of friction)、帽子偏心率(Cap eccentricity)、初始屈服面位置(Initial yield surface position)、过渡面半径(Transition surface radius)、流动应力比(Flowstress ratio)，在帽子区域采用相关流动法则，在剪切破坏和过渡区域采用非相关流动法则。

Mohr-Coulomb模型屈服面函数为

F=Rmcq-ptanφ-c=0

(12)

(13)

cos(3θ)=r3/q3

(14)

以上式中，φ为材料内摩擦角，c为黏聚力，Rmc(θ,φ)为控制屈服面形状的函数，θ为极偏角，r为第三偏应力不变量。

Drucker-Prager模型屈服面函数为

F=t-ptanβ-d=0

(15)

(16)

以上式中，β为屈服面在p-t应力空间上的倾角，与φ有关，k为三轴拉伸强度与三轴压缩强度之比，d为屈服面在p-t应力空间t轴上的截距。

2.2 接触关系

桩土之间的接触关系为具有主从关系的面对面接触，以桩的接触面作为主面，土体接触面作为从面，采用罚函数算法(Penalty algorithms)，垂向接触属性为“硬”接触(Hard contact)，切向接触可有限滑移(Finite sliding)，滑移摩擦由Coulomb接触法则控制，桩土间的Coulomb摩擦系数为0.6。

2.3 荷载及边界条件

整体模型受到的外部荷载主要为重力和静水压力，初始条件主要有重力、孔隙比和孔隙水压力的分布，边界条件包括侧边界的水平位移约束(U1=0)、底边界的垂直位移约束(U2=0)、桩靴体的初始平动和转动约束。为了控制整体模型在桩靴贯入之前不发生较大变形，首先设定地应力平衡分析步(Geostatic step)，在考虑桩土质量、形状尺寸和整体受力情况下，使土体均匀沉降，达到地应力平衡状态。桩靴的贯入采用位移贯入法，在土壤力学分析步(Soils step)中，通过指定桩靴体的竖向位移-时间(U2-t)函数来实现，贯入速率不宜太快，在黏土中小于0.1 m/s，在无黏土中小于0.05 m/s，且开始时以缓慢贯入过渡。由于插桩过程是荷载的快速加载过程，孔隙水压力来不及消散，因此，采用瞬态(Transient)孔隙水压响应方式。

2.4 应力平衡方程和渗流连续方程

土体应力平衡方程采用虚功原理来表示，在某一时刻土体的虚功与作用在该土体上作用力(体力和面力)产生的虚功相等

(17)

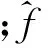
fω=(sn+nt)ρωg

(18)

在有限元法中，采用拉格朗日方程对该方程进行空间离散。

渗流连续方程是由同一时间内流入土体的水量等于土体的体积变化量这一连续条件来建立的

(19)

式中：vω为流体的平均流速；n是边界S的外法线；ρω0为参考密度(Reference density)。

该连续方程采用反向欧拉近似法进行时间积分，孔隙水渗流服从Darcy定律或Forchhermer定律。Forchhermer定律的表达式为

(20)

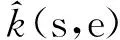
2.5 网格及模型尺寸

本文采用的桩靴整体类似于陀螺形，下部呈锥体，最大截面直径为9.14 m。土体范围总宽度为100 m，土体深度为40 m。桩靴周边的网格单元尺寸为0.5 m，向远处逐渐增大至5 m，以节省计算成本。整个模型共有节点738个，单元683个(图1)。

2.6 模型验证

图1 土体及桩靴的有限元网格Fig.1 FEM meshes of spudcan and soil

对数值模型进行验证，并修改和完善模型参数，可以提高模型的有效性和可信度。鉴于自升式钻井船的插桩过程极其复杂，直接观察其插桩阻力随深度的变化情况，目前尚很难实现，而进行室内模型实验不失为一种可行的验证方案。目前业界完成的模型实验并不多，本文以Craig和Chua完成的在离心机中模拟桩靴贯入黏土的试验[20]来验证数值模型，分别选取了不排水抗剪强度为39 kPa、63 kPa时的实验结果进行验证，由于是在黏土中进行实验，且贯入深度较浅，因此，验证时也加入了Skempton公式的计算结果，作为对比参考。

3 有限元数值结果分析

3.1 均质黏土中土体的破坏形式及承载力计算

2-a 39 kPa黏土中 2-b 63 kPa黏土中图2 桩靴贯入数值模型的离心机实验验证曲线Fig.2 Verification curve between FEM and experiment results

在均质黏土中，对桩靴贯入10 m深度地层的插桩现象进行了有限元仿真模拟，采用的土体黏聚力从10～80 kPa范围进行了试算，本文选取c=25 kPa时的模拟结果进行地基土的破坏形式、荷载影响深度及承载力计算方法的分析。c=25 kPa的黏土处于软(soft)和中等(firm)状态的界限，在中国渤海海域也较为常见，具有典型代表性。

(1)地基土破坏形式。插桩过程中的地基土破坏形式可用模拟结果中的等效塑性应变(PEEQ)来反应，图3给出了插桩深度分别为1.0 m、2.8 m、4.0 m时的地基土PEEQ等值线分布。可以看出，当插桩至2.8 m之前时，桩靴底部存在贯通的塑性应变区，并延伸到海底面，此时地基易出现整体滑移，地基土的破坏形式类似于整体剪切破坏；当插桩深度在2.8～4.0 m范围时，桩靴边缘的地基土体塑性应变较大，但在桩靴底部并未贯通，地基土的破坏形式类似于局部剪切破坏；当插桩深度大于4.0 m时，地基土中不再形成延伸至海底面的塑性区，桩靴四周的土体发生冲切破坏，使桩靴连续刺入土中，极限平衡区限制在微小的局部范围内，地基土的破坏形式类似于冲剪破坏。

图3 均质黏土中不同深度处等效塑性应变(PEEQ)分布图Fig.3 PEEQ contour line in different depths in homogeneous clay

由此可见，当在黏土中插桩深度过小时，地基容易出现滑移，对自升式钻井船的抗倾稳性不利，因此，在实际插桩时，除了承载力满足条件，还要保证一定的插桩深度。

(2)插桩荷载影响深度。本文以地基土的受压竖向位移(U2)和剪切应力(S12)的分布范围来表示插桩荷载的影响深度。当插桩至1.5 m深度时，土体U2和S12的分布范围开始与桩靴尺寸表现出较好的线性相关，当插桩至4.0 m以下深度时，即地基土的破坏形式类似于冲剪破坏时，U2和S12的分布范围与桩靴尺寸的比例基本趋于固定，图4给出了插桩深度为5 m时的U2与S12分布。土力学中有时将s/b=0.01所对应的荷载作为承载力特征值，本文在此以U2=0.01B作为插桩荷载影响深度的判别标准，模拟结果显示，U2=0.09 m(0.01B)的土体分布范围形似灯泡，其底界面距桩靴最大截面宽度处的垂向距离约为3.0倍基础宽度，桩靴底部土体的剪切应力分布范围似肾形，3.0B深度处的S12值约为10 kPa，为土体本构模型中黏聚力25 kPa的0.4倍。

图4 均质黏土中土体竖向位移(U2)和剪切应力(S12)分布图Fig.4 Distribution of U2 and S12 in depth of 5.0 m in homogeneous clay

(3)地基承载力计算。图5给出了c=25 kPa时的有限元模拟地基承载力曲线及各公式计算结果，模拟曲线形态近似于a<1的幂函数，在浅部地层中曲率较大，随着插桩深度的增大，其曲率逐渐趋小。

图5 均质黏土中有限元模拟与公式计算结果对比(c=25 kPa) Fig.5 Comparison between FEM simulation and formulas calculation in homogeneous clay

有限元数值模拟结果与Skempton公式、SNAME规范公式的计算结果相交于2.2～2.5 m深度范围，此后其走势渐趋一致，而SNAME结果与数值模拟结果更为接近。在2.2～2.5 m以浅，公式计算结果较大，这是因为Skempton公式和SNAME规范公式都假定基础已经埋置于特定深度、基础侧限存在边载土压力，而在数值模拟中，桩靴是自海底面开始贯入，贯入时并不存在边载，而且，在贯入深度较浅时，桩靴底部的塑性应变区贯通，不利于两侧土体边载土压力的发挥，因此，其承载力开始贯入时几乎为0，然后随着边载土压力的逐步发挥，承载力呈曲线形逐渐增大。在2.2～2.5 m以下深度，公式计算结果的数值偏小，这主要是由于公式假定极限承载力为地基土发生塑性破坏时的承载力，而数值模拟的插桩过程不断地破坏地基土，又不断下适持力层，极限承载力发生在地基土发生了塑性破坏之后，再加上土体本构模型属于弹塑性模型，因此模拟得出的数值更大。从桩靴贯入的形式来看，数值模拟的过程更接近实际插桩过程，在实际工程中，本文认为，Skempton公式和SNAME规范公式都可用于计算桩靴贯入均质黏土中的地基承载力，但在插桩深度过浅时(如2.5 m以浅深度)，公式的有效性会降低，本文建议忽略较浅部地层中的计算结果，将插桩深度设定在2.5 m以下深度，也有利于提高桩靴的抗滑移和抗倾稳性。

API RP2A规范推荐的计算公式属于桩基础公式，其计算结果与模拟结果的曲线相交于约6.9 m深度处，且其计算结果偏大，在实际工程中建议慎用。

3.2 均质砂土中土体的破坏形式及承载力计算

在均质砂土中，对桩靴贯入10 m深度地层的插桩现象进行了有限元仿真模拟，采用的土体内摩擦角从20～35°范围进行了试算，本文选取φ=24°时的模拟结果进行地基土的破坏形式、荷载影响深度及承载力计算方法的分析。在中国渤海海域，浅层沉积的砂土多为稍密—中密状态的粉砂或细砂，砂质粉土也较为常见，其土力学性质更接近粉砂，这些土的内摩擦角都较小。

(1)地基土破坏形式。图6给出了插桩深度分别为4.0 m和10.0 m时的地基土PEEQ等值线分布。当插桩深度较浅时，桩靴底部存在贯通的塑性应变区，并延伸到海底面，地基土破坏形式类似于整体剪切破坏，这与prandtl在较硬地基土基础浅埋情况的地基土破坏形式的认识一致[21]。当插桩至10.0 m以下深度时(略大于1倍桩靴直径)，逐渐转变为类似冲剪破坏。

(2)插桩荷载影响深度。图7给出了插桩深度为5 m时的U2与S12分布，模拟结果显示，U2=0.09 m(0.01B)的土体分布范围形似烧杯，其底界面距桩靴最大截面宽度处的垂向距离约为3.0B，桩靴底部土体的剪切应力分布范围似梨形，3.0B深度处的S12值约为30 kPa，为该深度处土体抗剪强度γ3.0Btanφ(97.6 kPa)的0.3倍。

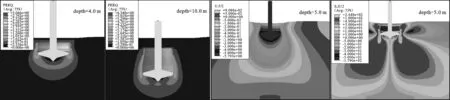
图6 均质砂土中不同深度处等效塑性应变(PEEQ)分布图Fig.6PEEQcontourlineindifferentdepthsinhomogeneoussand图7 均质砂土中土体竖向位移(U2)和剪切应力(S12)分布图Fig.7DistributionofU2andS12indepthof5.0minhomogeneoussand

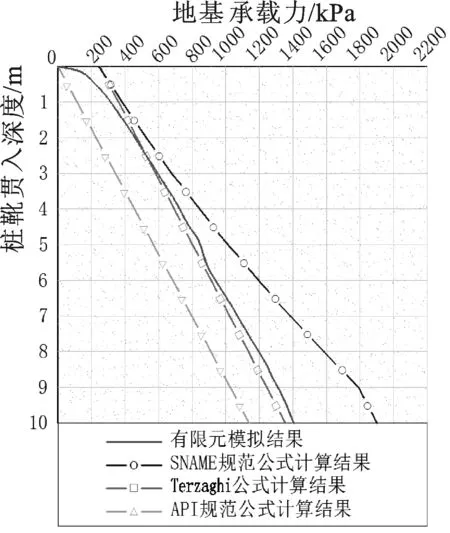
图8 均质砂土中有限元模拟与公式计算结果对比(φ=24°)Fig.8 Comparison between FEM simulation and formulas calculation in homogeneous sand

(3)地基承载力计算。图8给出了φ=24°时的有限元模拟地基承载力曲线及各公式计算结果，模拟曲线形态近似为直线，仅在1.0 m以浅为曲线。

有限元数值模拟结果与Terzaghi公式相交于约2.5 m深度处，此后无论是数值还是走势都非常接近，这说明Terzaghi公式适宜于计算桩靴贯入均质砂土中的地基承载力，在2.5 m以浅，公式的计算结果偏大，仍是由于公式考虑了边载土压力的影响，而在数值模拟中，这是逐步产生和发挥作用的，因此，本文同样建议在应用Terzaghi公式时，忽略较浅部地层中的计算结果。

SNAME公式的计算结果偏大，曲线走势也与数值模拟结果不一致，这可能是由于该公式在第二项同时考虑了有效上覆压力p0′和深度修正系数dq的影响，这2个参数都随深度的增加而增大，本文不建议在均质砂土中应用该公式。顺便一提，当不考虑dq的影响时，SNAME公式的计算结果与模拟结果更为接近，只是数值略大一点。

API RP2A规范公式属于桩基础公式，其计算结果尽管在曲线走势上与数值模拟结果接近，但其数值偏小，本文不建议应用。

4 结语

通过以有限元数值方法模拟具桩靴自升式钻井船贯入地层一定深度的动态过程，取得了地基土破坏形式、插桩荷载影响深度、地基承载力计算方法等多方面认识，按照地基土性质的不同，可分别总结为：

(1)在均质黏土中插桩时，随着插桩深度的增大，地基土先后经历了整体剪切破坏、局部剪切破坏、冲剪破坏3种破坏形式，插桩荷载的影响深度约为3.0B，Skempton公式和SNAME规范公式都适宜于计算均质黏土中桩靴荷载的承载力。

(2)在均质砂土中插桩时，地基土的破坏形式主要表现为整体剪切破坏，插桩荷载的影响深度约为3.0B，Terzaghi公式适宜于计算均质砂土中桩靴荷载的承载力。

(3)Skempton公式、SNAME规范公式(均质黏土中)、Terzaghi公式，都可用于计算桩靴贯入均质土时的地基承载力，但在插桩深度过浅时，受边载土压力未完全发挥等因素影响，公式的计算结果往往偏大，建议忽略较浅部地层中的计算结果，这也有利于提高桩靴的抗滑移性和抗倾稳性。

(4)将有限元数值模拟方法应用于海洋岩土工程仿真模拟，可适应复杂的工程边界条件和地基土类型，在研究难以观测的工程现象时极为方便，而在模型的建立与修缮方面无论是成本还是效率都远甚物理试验模型，因此具有无可替代的优势。

参考文献：

[1] 季春群, 孙春昌. 自升式钻井船地基承载力抗倾稳性及桩腿插深分析[J]. 上海交通大学学报,1996, 30(3):79-85.

JI C Q,SUN C C. Analysis of Stability Against Overturning and Foundation Bear Force for Jack-Up Rig[J]. Journal of Shanghai Jiaotong University,1996, 30(3):79-85.

[2] 胜利石油管理局钻井工艺研究院海洋所.中油海5钻井平台操作手册[R].东营: 胜利石油管理局,2007.

[3]中国船舶工业集团公司第708研究所.中油海62平台操作手册[R].东营: 胜利石油管理局,2009.

[4]Skempton A W. The bearing capacity of clays[J]. Building Research Congress,London,1951,1:180-189.

[5] 钱家欢,殷宗泽.土工原理与计算:第二版[M].北京:中国水利水电出版社, 1996.

[6] SNAME. Guidelines for site specific assessment of mobile jack-up units[M]. New Jersey: Society of naval architects and marine engineers, Technical and Research bulletin5-5A,1997.

[7] American Petroleum Institute. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design (API RP2A-WSD)[M]. New York: American Petroleum Institute,2004.

[8] 殷齐麟,董胜,樊敦秋.复杂地层中自升式平台插桩的数值模拟[J].工程力学, 2016, 33(9):204-210.

YIN Q L, DONG S, FAN D Q. Numerical Simulation of Penetration of Jack-up Platform in Complex Foundation Soils[J].Engineering Mechanics, 2016, 33(9):204-210.

[9] 王金昌, 陈页开.ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社,2006.

[10] 费康, 张建伟. ABAQUS在岩土工程中的应用[M].北京:国水利水电出版社, 2010.

[11] Hu Y, Randolph M F. A practical numerical approach for large deformation problems in soil [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1998, 22(5): 327-350.

[12]Mehryar Z, Hu Y. Penetration analysis of spudcan foundation in Ncclay [C]//Proceedings of the 12th International Offshore and Polar Engineering Conference.Kitakyushu, Japan, 2002:679-684.

[13] Erichson H L, Drescher A. Bearing capacity of circular footings [J]. ASCE, Journal of Geotechnical Engineering, 2002, 128(1): 38-43.

[14] Kellezi L, Stromann H. FEM analysis of jack-up spudcan penetration for multi-layered critical soil conditions [C]//Sarah M.Proceeding of BGA International Conference on Foundations.Dundee, Scotland, 2003:410-420.

[15] Kellezi L, Kudsk G. Spudcan Penetration FE Simulation of Punch-through for Sand over Clay [C] // Kellezi L.Proceeding of the 12th International Jack-up Conference.London, England, 2009:336-348.

[16] Kellezi L, Kudsk G. Spudcan Penetration FE Simulation of Punch-through for Sand over Clay [C]// Kellezi L. Proceeding of the 12th International Jack-up Conference.London, England, 2009:336-348.

[17] LIU J, HU Y X, KONG X J. Deep penetration of spudcan foundation into double layer soils[J]. China Ocean Engineering, 2005, 19(2): 309-324.

[18] Qiu Gang, Henke S, Jurgen Grabe. 3D FE analysis of the installation process of spudcan foundations [J]. Frontiers in offshore Geotechnics II, 2010:685-690.

[19] Qiu Gang, Jurgen Grabe. Numerical Simulation of the Deep Penetration Process of Spudcans into Sand Overlaying Clay Using the Extended Hypoplastic Models [C]//HUANG F J.Proceedings of the 22nd International Offshore and Polar Engineering Conference.Rhodes, Greece, 2012:681-688.

[20] Craig W H,Chua K. Deep Penetration of spudcan foundation in sand and clay[J]. Geotechnique, 1990,40(4): 541-556.

[21] 陈希哲. 土力学地基基础[M]. 北京：清华大学出版社，2000.