MEMS陀螺随机误差建模与Kalman滤波方法

张伟

（中国电子科技集团公司第二十研究所，西安 710068）

0 引言

随着现代微电子与微加工工艺的迅速发展，基于微机电系统（Micro Electromechanical System，MEMS）技术的MEMS陀螺仪迅速发展起来，相比于其他类型的陀螺仪，MEMS陀螺仪具有体积小、功耗低、成本低、重量轻等优点。目前，MEMS陀螺仪己经在众多军民用、用领域得到广泛应用，因此MEMS陀螺仪具有巨大的发展潜力和发展价值。但是由于制造工艺和设计水平的原因，目前MEMS陀螺仪相比其他陀螺其输出信号具有随机噪声大、稳定性差，易受温度等外界因素的影响等缺点，这直接影响了系统的测量精度，因此为提高稳定精度，进行有效的信号去噪处理消除误差，是非常必要的。

时间序列模型方法是对陀螺仪的各种随机噪声进行整体考虑，利用白噪声驱动下的 ARMA模型的线性组合对 MEMS陀螺仪输出的随机误差进行拟合，通过选取合适阶次的模型，在时域内对陀螺仪的随机误差的统计特性进行建模，是针对陀螺仪随机漂移问题的常见方法。

Kalman滤波是一种线性、无偏、以误差方差最小为估计准则的最优估计算法。在对随机误差建模后，通过Kalman滤波进行最优估计，可以有效降低陀螺信号随机漂移。

1 MEMS陀螺数据预处理和数据检验

按照时间序列建模的要求，数据应该是零均值、正态、平稳的，所以建模前应该对数据进行预处理和数据检验。这包括奇异点的剔除、常值分量提取和趋势项的剔除、平稳性检验和正态性检验。

1.1 数据预处理

本文所用数据为挪威SENSONOR公司生产的STIM210型陀螺仪在常温、静态条件下采集，采样频率10Hz。MEMS陀螺原始漂移信号如图1所示。

从图1可以看出原始漂移信号中没有明显的奇异点，如果有奇异点，可以采用拉伊达准则（又称3σ准则）剔除[1]，简单讲，就是将信号与采样

信号的均值做比较，如果差值的绝对值大于采样数据标准差的3倍，则认为该数据为奇异点，应该予以剔除。

再次，现阶段的高职生大多属于独生子女，且在互联网技术的发展环境中成长，因此他们接受外界信息的来源更加广泛，接收到新思想、新观念也比较多，在这一条件下，他们很难形成系统的、全面的、有效的判断，模糊的是非判断会严重影响他们的思政观念，容易出现跟风的情况，不能够明辨是非，凭借意气用事。

图1 MEMS陀螺原始漂移信号

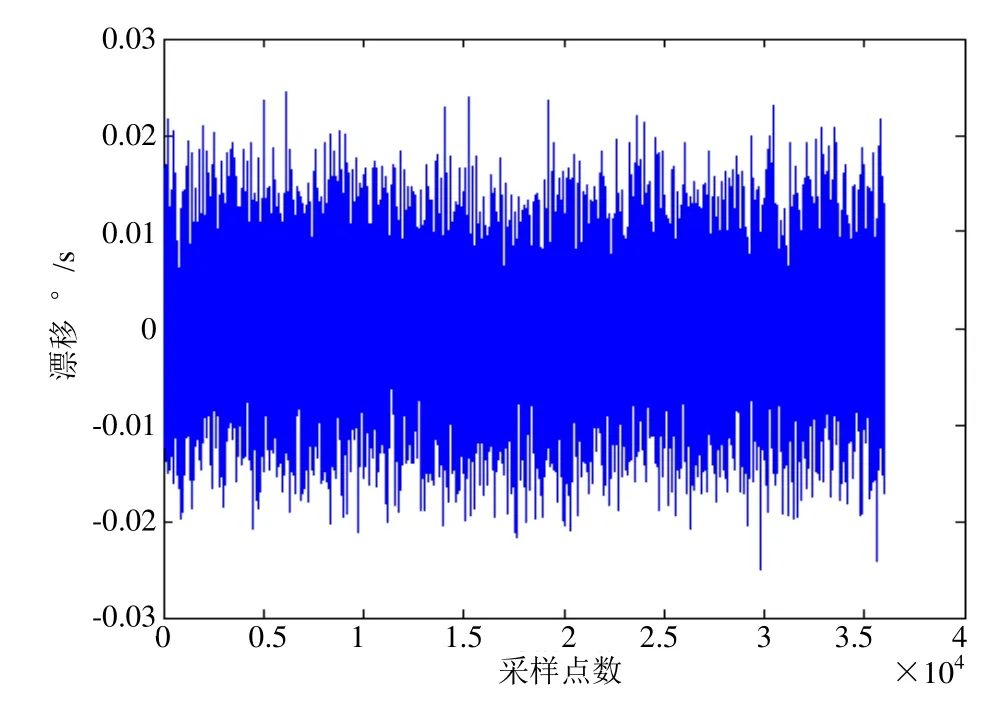
图2 去除常值分量的MEMS陀螺漂移信号

从原始漂移信号中还可以看出，数据中含有常值漂移分量和随机漂移分量，应该将常值漂移分量去除，是信号达到零均值的要求。本文采用实时平均算法对数据进行处理，采用当前时刻以及前面的50个点作为当前时刻的平均值，将当前时刻的采样值减去当前时刻的平均值，就可以得到零均值的时间序列。

1.2 数据检验

去除常值漂移后的序列即为 MEMS陀螺随机漂移信号，此时的漂移信号由于外部环境和MEMS陀螺本身的因素，还可能存在趋势项，所以还应该对信号进行进一步的数据检验。

1.2.1 平稳性检验

随机序列的平稳性检验方法按是否需要加入额外参数的区别可以分为参数检验法和非参数检验法两种，本文对陀螺漂移数据的平稳性检验采用非参数检验法中的轮次检验法。假设一个序列由随机变量Xt的N个观察值或一段时间内的采样均值组成，把Xt的观察值按与去除常值漂移后总体均值差值的正负性分成两个互斥的类，设定每个观察值一组同类的观察值的前面与后面为不同类的观察值或没有观察值即为一个轮次。得到该组数据的轮次值r后，查询轮次分布表，当显著水平α=0.05时，得到判断一组序列平稳的r值可接受范围，r值在可接受范围内则认为序列是平稳的，反之数列不平稳[2]。不平稳序列一般进行一到二阶差分，即可转换为平稳时间序列。

1.2.2 正态性检验

正态检验常用的方法是检验数列的偏态系数ξ（三阶距）和峰态系数υ（四阶距）是否满足正态随机变量的特性。偏态系数和峰态系数的定义为[3]：

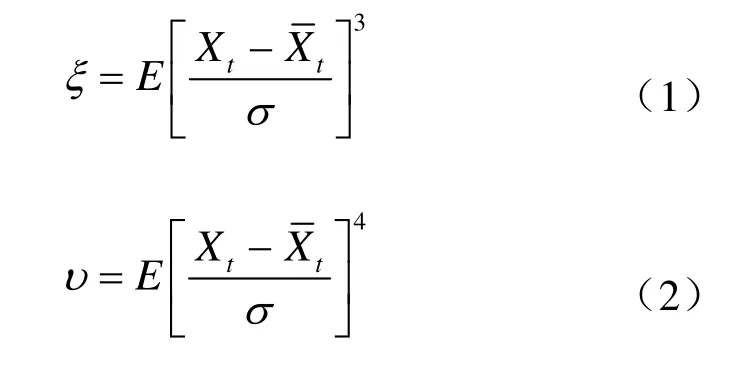
如果序列为正态，那么偏态系数ξ=0，峰态系数υ=3，具体计算时ξ和υ的估计值可用以下两式表示：

式中，为数列的均值，σ为数列的标准差。

图3 数列概率密度分布曲线图

本文采用一种更直观的方法，通过统计数列中各个量概率密度，并绘制数列的概率密度曲线图，便能简易的判断该组平稳数据是否服从正态分布。

2 MEMS陀螺随机漂移误差的时间序列建模

经过预处理的时间序列就可以用时间序列模型来建模，自回归滑动平均模型表示的是随机过程t时刻的观测值与t时刻之前的p个观测值存在相关性，且与t时刻的q个白噪声也存在着相关性，反映了t时刻的观测值与t时刻之前的各观测值存在自回归关系，同时也反映了t时刻的观测值与t时刻之前各白噪声之间的滑动平均关系。该模型用表示为：

式中：p—自回归模型AR阶数；q—滑动平均模型MA阶数；Xt—时间序列信号；ωt—白噪声序列。

特别地，当q=0时，模型退化为p阶AR模型，当p=0时，模型退化为q阶MA模型。

在建模前，首先要确定模型的类型和阶数，常用的方法有AIC准则和BIC准则，本文采用前者。MEMS陀螺漂移模型的阶次都比较低，一般不超过2～3阶，所以可以在阶数2～3的模型中选择AIC最小值对应的模型[4]。不同阶数模型对应的AIC值见表 1，所以本文选用 AR(1)模型对陀螺漂移进行建模。

表1 不同模型的AIC值对照表

由 MATLAB仿真软件求得数列 AR(1)模型的表达式如下：

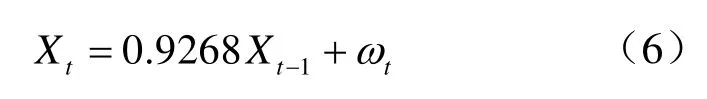
原始观测数据、AR(1)模型预测数据、和AR(1)拟合残差如图4、图5和图6所示。

3 Kalman滤波

卡尔曼滤波是一种线性、无偏、以误差方差最小为估计准则的最优估计算法，它的数学模型是一阶的，特别适合计算机处理[5]。

卡尔曼滤波问题可以描述如式（7）和式（8）。

图4 原始观测值

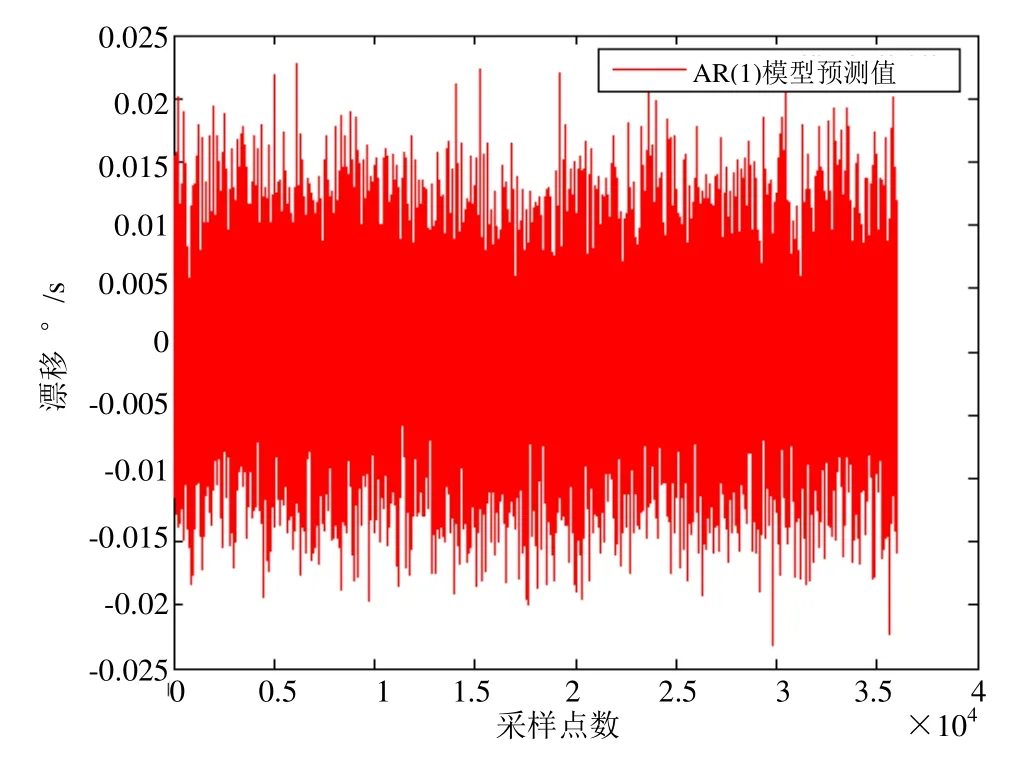
图5 AR(1)模型预测值

图6 AR(1)模型拟合残差

式（7）和式（8）分别为系统的状态方程和量测方程。假设：

（1）系统噪声Wk（方差为Qk）和量测噪声Vk（方差为Rk）是零均值白噪声或高斯白噪声序列，

（2）Wk与Vk互不相关，k≥0；

（3）系统的初始状态X0是具有已知统计特性的随机向量，其均值和方差为已知；

（4）Wk与Vk均与初始状态X0无关，k≥0

就可以构造以下标准卡尔曼滤波方程组：一步预测方程：

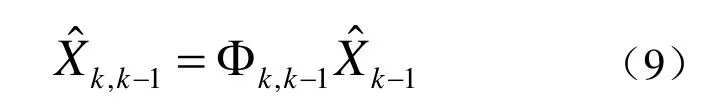
一步预测误差方差：

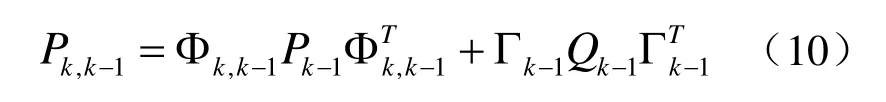
滤波增益方程：

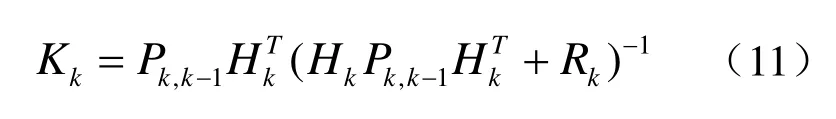
滤波方程：

滤波误差方差：

4 滤波结果

本文中，Pk的初值选为单位阵也就是1，Xk的初值选为量测初值，为 AR(1)模型中残差信号的方差，Rk为量测信号方差。这样就可以利用上面的Kalman滤波递推公式进行滤波。

将预处理后零均值、平稳、正态的陀螺原始信号作为滤波器的输入，输出原始数据和卡尔曼滤波后的数据对比如图 7所示，滤波前数据的方差为滤波后数据的方差为

5 结论

本文对 MEMS陀螺在静态下的信号进行了预处理，包括奇异值去除、常值漂移去除，平稳性检验、正态性检验，使数据满足时间序列建模的要求。并以此为基础用AR(1)模型进行了随机误差建模和Kalman滤波。结果表明，该方法能有效地减小MEMS陀螺的随机误差，具有一定的工程应用价值。

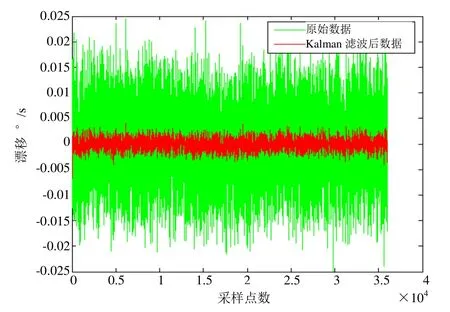
图7 Kalman滤波后数据与原始数据对比

参考文献：

[1]霍元正.MEMS陀螺仪随机漂移误差补偿技术的研究[D].东南大学硕士学位论文, 2015.

[2]吴峰.两轴平台稳定系统中 MEMS陀螺误差建模与分析[D].天津大学硕士学位论文, 2012.

[3]蒙涛, 王昊.MEMS陀螺误差建模与滤波方法[J].系统工程与电子技术, 2009,31（8）:1944-1947.

[4]吉训生, 王寿荣.MEMS陀螺随机漂移误差研究[J].宇航学报, 2006, 27（4）: 640-642.

[5]罗建军, 马卫华, 袁建平, 岳晓奎.组合导航原理与应用[M].西安: 西北工业大学出版社，2012.