爆破振动作用下铁路路基动力响应规律研究*

叶海旺 余 波 雷 涛 李 宁 王其洲 龙 梅

(1.武汉理工大学资源与环境工程学院；2.矿物资源加工与环境湖北省重点实验室；3.武汉理工大学图书馆)

随着我国经济建设的迅速发展和基建投入的增加,作为岩土工程施工中经济有效的重要手段，工程爆破技术不断被运用到这些基础设施建设当中[1]。近年来，邻近铁路路基的爆破开挖时有发生，由此产生的爆破振动对铁路路基坝安全性的影响一直受到铁道及相关部门的关注。但由于爆破振动的复杂性和传播介质的多样性，铁路路基坝在爆破荷载作用下的安全性分析尚未形成科学的标准。在进行工程爆破时产生的地震是一种十分常见的动力学现象，爆破地震波通过周边介质向四周传播，从而引起周边岩土介质的振动，遇到铁路路基坝时会与其发生相互作用，当振动达到足够强度时将直接威胁到路基坝的稳定性和安全性。

目前，对铁路路基动力学研究主要有理论分析、数值模拟及试验。在坝体动力响应的研究方面，刘军等[2]将混凝土、心墙、反滤层与堆石体作为坝体的简化材料，模拟了爆炸荷载作用下土石坝动力响应的特性；黄剑锋等[3]利用ABAQUS软件建立等效线性粘弹性模型进行地震响应分析,重点分析坝体的反应加速度、动位移、动剪应力、动剪应变和残余变形等动力反应情况；胡旬等[4]采用溃坝风险分析、渗流模拟、稳定性分析等多种方法研究在爆破震动波作用下的尾矿坝稳定性问题，确定影响尾矿坝安全的主要因素，判明在不同工况条件下尾矿坝稳定性的安全边界条件。但对于铁路路基坝这种特殊坝体，大多学者研究铁路路基的动力响应分析均从列车荷载出发，孙常新等[5]采用有限元分析方法计算分析了铁路路基的动力响应(位移)在列车荷载作用下的分布规律，分析了影响路基位移值的各种因素，对路基动力响应(位移)随车速变化的“双峰现象”成因进行了分析。尹壮飞等[6]利用Fortran语言对列车荷载作用下高速铁路路基的动力响应进行深入的研究，从土体深度、列车速度以及轴重等方面对高速铁路路基的动力响应进行研究。董亮等[7]将三维一致粘弹性人工边界单元引入ABAQUS有限元软件，验证了该人工边界单元在无砟轨道高速铁路路基动力响应分析方面的有效性。然而对爆破作用下铁路路基坝动力响应方面研究较少。本文以丽水市水阁至腊口新建公路的路堑开挖爆破工程为背景，采用理论分析、现场试验和数值模拟相结合的方法，对爆破地震波作用下的铁路路基坝动力响应进行分析，以期提出安全合理地控制标准。

1 工程概况

丽水市水阁至腊口公路工程第三合同段起点位于大梁山隧道中部ZK8+434(YK8+417)处，线路全长约3.825 km。采用一级公路标准，设计速度为80 km/h，路基宽24.5 m，分离式路基宽12.25 m。

施工过程中边坡修整、路堑开挖等工程均需要进行爆破施工，其中K10+617.259～K10+891段边坡开挖高度达49.2 m，最高边坡为五级边坡，坡体主要由强风化、中风化、微风化凝灰质粉砂岩组成。强风化岩为碎石状，镶嵌碎裂结构，厚2.5～3.0 m；中风化岩为裂隙块状结构，属较坚硬岩，岩石风化较弱。中心最大开挖高度约51.3 m，边坡最大开挖高度达49.2 m左右，每层爆破开挖高度为10 m。爆破区域距离金温货线路基最短距离为336 m，高程差为30～50 m。公路路堑爆破开挖与铁路路基位置关系见图1。

图1 公路路基挖方与铁路平面位置关系示意(单位：m)

2 现场爆破测试

在铁路路基坝坡顶布置监测点，采用Blast-UM爆破振动测试仪，监测数据见表1。

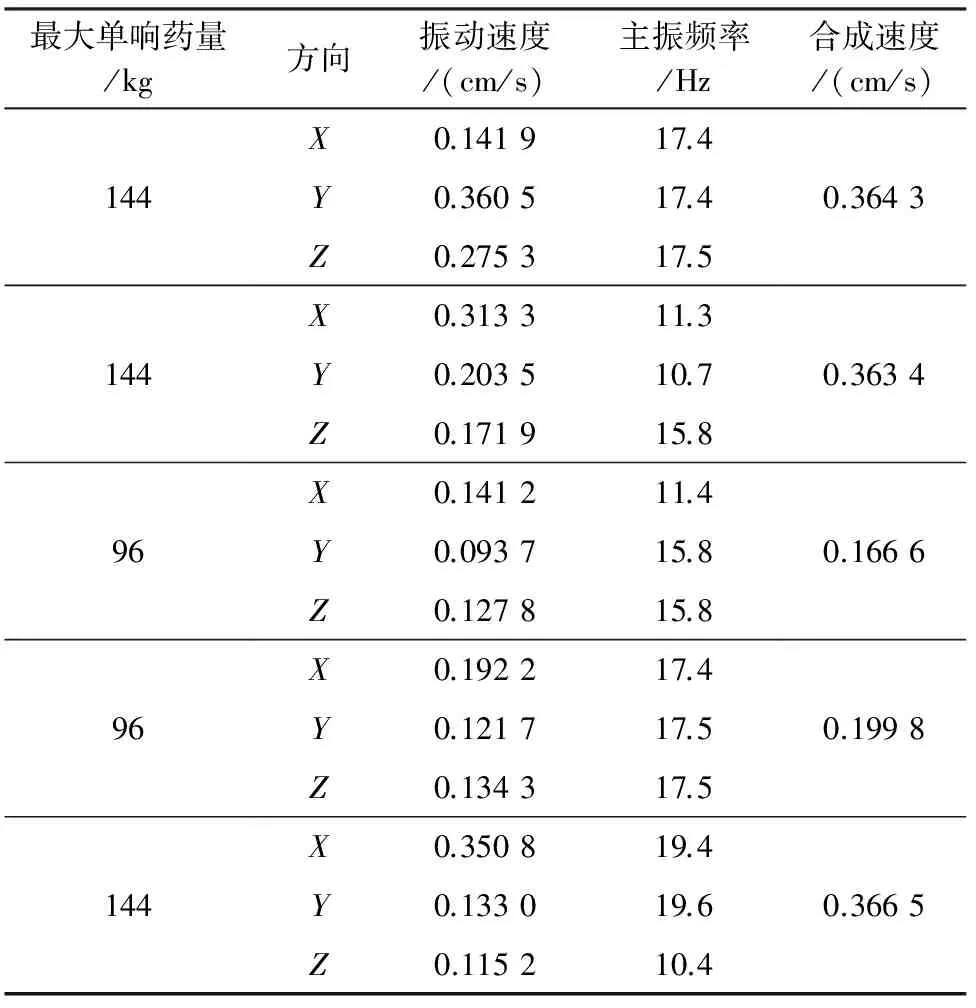
表1 部分现场实测数据

从表1可以看出，由于爆破区域距离铁路路基较远，爆破震动通过复杂的地质条件传播到路基，引起铁路路基震动，频率为10～20 Hz，所测数据可为爆破震动下铁路路基动力响应提供数据参考。

3 有限元模型及分析

3.1 模型建立

路基工程采用填料、石料、混凝土、水泥砂浆、钢材及土工合成材料等，应根据其类型、特征、性能、适应范围和应用结构形式、应用环境等确定[8]。依据该地区铁路路基坝实际情况，建立铁路路基坝模型，见图2。模型分为4层，从上至下每层高度分别为0.6，1.7，2.4，1.1 m。每层根据不同配比进行铺设，其材料参数见表2。

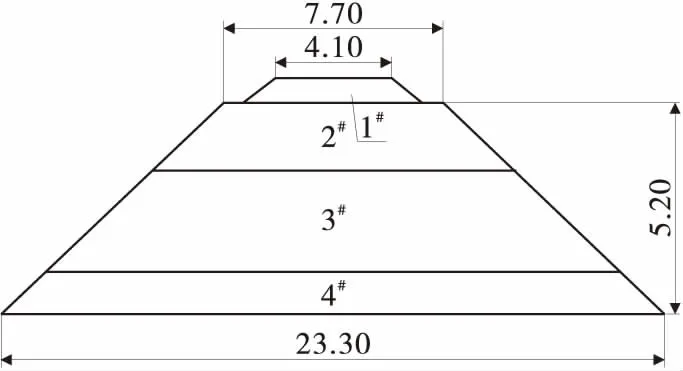
图2 铁路路基坝几何模型断面(单位:m)

分层编号密度/(kg/m3)弹性模量/MPa泊松比内聚力/kPa内摩擦角/(°)1#2500230．00．18--2#191029．30．3042323#188038．60．3238284#186010．70．353020

为简化分析，建立50 m长铁路路基坝模型，采用莫尔-库仑准则。对该模型进行网格划分，共有290 072个节点，28 800个单元，铁路路基坝有限元模型见图3。

图3 铁路路基坝模型

3.2 模态分析

在受到外界激励荷载时，结构运动状态取决于其物理特性，包括质量分布、弹性性能分布及耗能机制。以适当的表达式来表示这些特性，形成数学模型，是动力学分析的基础。研究铁路路基坝结构爆破地震波的动力响应时，其自身特性是必须考虑的因素。结构的自身特性反映在其固有频率和振型，与外部载荷无关[9]。模态振型是描述结构上点与点相对位置关系的一组比值，某阶固有频率作用下结构由振动发生最大形变的形态属于结构的固有属性。如果结构的组成构造、材料属性、约束条件没有发生改变，结构的振型也将维持原状。

采用ANSYS对铁路路基坝进行模态分析，分别为建模、加载、分析计算、后处理4个步骤，并采用Block Lanczos分块法查看模型前6阶模态结果，分析截止频率设置为9 999 Hz，计算得到坝体结构自振频率和振型，模型前6阶模态结果见表3，固有振型见图4。

表3 铁路路基坝前6阶模态分析结果

图4 铁路路基坝模型前6阶振型

图4显示铁路路基坝的第一阶最大位移出现在模型顶部的中间位置，第二阶出现在路基坝的护坡靠两端位置，为扭转变形，第三阶出现在护坡中间部位，第四～第六阶振型比较复杂。通常所说的结构的共振频率指的是结构的一阶固有频率，该铁路路基坝的一阶固有频率为3.737 9 Hz。

4 铁路路基坝动力响应分析

爆区铁路路基坝的爆破地震效应本质上是坝体对爆破产生振动的动力响应问题，具体表现在坝体受到地面振动作用时导致的应力、位移、速度等。爆破地震波特性可用质点的速度峰值、主频和持续时间来描述，它们是爆破地震波引起结构产生动力响应的主要因素。

利用有限元软件LS-DYNA分析爆破振动作用下铁路坝体结构的动力响应，对模型施加重力,和实测爆破地震波进行相关动力分析。对铁路路基坝模型底部及两端施加无反射边界，且在底部施加垂直于路基截面的约束，在路基模型底部施加爆破应力波，通过调整爆破地震波信号的特性参数来研究爆破地震波振速对坝体的爆破地震响应的变化规律。

4.1 铁路路基坝随地震波幅值响应规律

为了分析对比地震波强度对结构的影响和破坏作用，研究爆破地震波振速幅值与坝体受力情况之间的关系，取11月4日实测的爆破地震波信号，取其时间为1 s且包含各项振动速度最大的数据，绘制如图5所示的速度时程曲线,幅值为0.36 cm/s,主频为17.5 Hz，时长为1 s，维持频率和时长不变，将实测振速调整为原始数据的2倍(0.72 cm/s)、4倍(1.44 cm/s)、8倍(2.88 cm/s)、16倍(5.76 cm/s)、32倍(11.52 cm/s)后再施加至模型底面节点。从坝体底部至顶部，每层顶部布置一个测点，共4个测点。测点布置见图6。

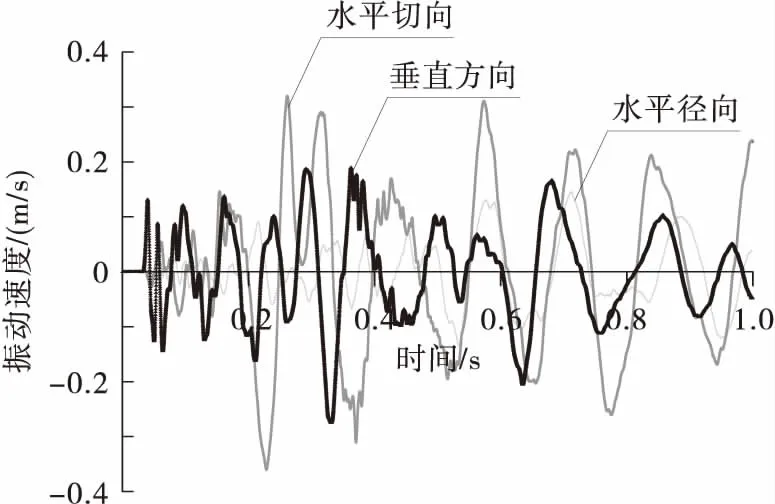
图5 爆破地震波三相速度时程曲线

图6 测点布置

在铁路路基坝底部加载不同幅值的爆破振动波，通过ANSYS建模、加载、计算后，运用LS-PrePost查看其响应结果，各测点竖直方向振动加速度幅值见表4。

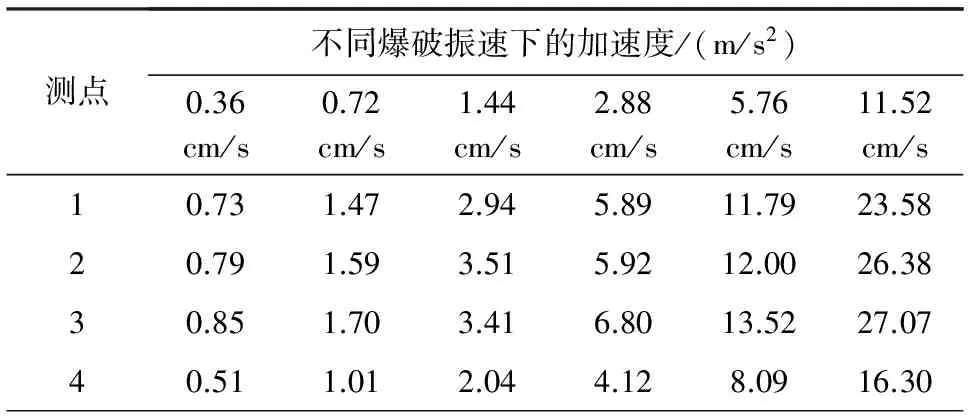
表4 不同爆破地震波幅值下坝体结构动力响应结果

由表4可以看出，保持爆破地震波频率和持续作用时间不变，随爆破地震波幅值的增大，各测点所测得的爆破地震波加速度也在增加，且与爆破地震波幅值成比例关系。测点3处振动加速度达到峰值，说明该处易发生破坏，需重点监测和保护。

4.2 爆破震动下铁路路基安全控制标准

目前，在爆破地震波破坏作用的研究中，大多采用地震烈度工程标准来评定建筑物的破坏状况，没有考虑结构类型、场地条件、地震波能量特性等因素。而爆破振动下铁路路基坝的安全控制标准并不完善，因此，研究并总结出一些爆破控制标准非常有意义。

容重增加法的基本原理是保持土体的抗剪强度指标C和φ为常数，通过逐步增加重力加速度G的方式，反复进行有限元分析，直至边坡达到临界破坏状态，而此时采用的重力加速度Gtrial与实际重力加速度G之比Ftrial可作为该边坡超载概念的安全储备系数，由于临界状态是通过容重的逐渐增加而达到的，故称为容重增加法[10]，其中Ftrial称为容重增加系数,即安全系数。重力加速度G值取9.8 m/s2。

根据我国《水利水电工程边坡设计规范》3.4.2 条文规定[11]，破坏后给社会、经济和环境带来重大影响的一级边坡，在正常运用条件下的抗滑稳定安全系数可取1.30～1.50。

从表4可知，当达到爆破振动16倍幅值5.76 cm/s 时，各测点爆破振动竖直方向加速度幅值最大为13.52 m/s2，Ftrial=1.38，在安全系数1.3～1.5范围内；当爆破振动超出16倍幅值时，可以判定已经发生破坏。

因此，经过多次试验模拟，为保证铁路路基坝安全，建议爆破振动速度控制在5.0 cm/s以内。

5 结 论

(1)利用ANSYS/LS-DYNA模态分析功能，根据坝体材料密度、弹性模量、泊松比等参数，通过选用合适的单元类型、网格、边界条件，分析了铁路路基坝的基本自振频率、振型等动力特性，得出一阶固有频率为3.74 Hz。

(2)铁路路基坝体在爆破振动作用下，其动力响应幅值随爆破地震波信号振速幅值的增大而增大，且增大系数与振速幅值增大系数总体保持一致。

(3)参考《水利水电工程边坡设计规范》中关于一级边坡的控制标准，提出爆破振动作用下铁路路基坝的安全控制标准为v≤5.0 cm/s。

[1] Alemdar Bayraktar,Ahmet Can Altunisik,Mehmet Ozcan.Safety assessment of structures for near-feild blast-induced ground excitations using operational modal analysis[J].Soil Dynamics and Earthquake Engineering,2012(39):23-36.

[2] 刘 军,刘汉龙,张 正.爆炸荷载下土石坝动力响应特征的数值模拟[J].防灾减灾工程学报,2010,30(1):10-16.

[3] 黄剑锋,张 峰,蔡云丽.尾矿坝动力数值模拟与永久变形[J].中州煤炭,2016(5):83-87.

[4] 胡 旬,卞宁东,曾霄祥.震动波作用下尾矿坝稳定性分析[J].现代矿业,2014,30(4):65-68.

[5] 孙常新,胡金虎,梁 波.准高速铁路路基动力响应数值模拟[J].计算力学学报,2010,27(1):173-176.

[6] 尹壮飞,曾鹏毅.某高速铁路路基动力响应研究[J].路基工程,2016(2):76-80.

[7] 董 亮,赵成刚,蔡德钩,等.高速铁路无砟轨道路基动力特性数值模拟和试验研究[J].土木工程学报,2008(10):81-86.

[8] 铁道第一勘察设计院.TB 10001—2005 铁路路基设计规范[S].北京：中国铁道出版社，2005.

[9] H Nohutcu，A Demir,E Ercan,et al.Investigation of a historic masonry structure by numerical and operational modal analyses[J].Structural Design of Tall and Special Buildings,2015,24(13):821-834.

[10] 肖 武.基于强度折减法和容重增加法边坡稳定性分析及工程应用[D].南京:河海大学，2005:23-25.

[11] 黄河勘测规划设计有限公司.SL 386—2007 水利水电工程边坡设计规范[S].北京：中国水利水电出版社，2007.