基于折叠法和灰关联分析的威胁雷达信号识别
,,
(国防科技大学电子对抗学院,安徽 合肥 230037)
0 引言
目前,各个国家对电子战的重视加快了电子战发展的进程,导致雷达辐射源的数目急剧增加,使得雷达所处的空间中雷达信号异常密集,信号密度大幅提高;另一方面,随着反侦察干扰技术的发展,现代雷达体制越来越先进,重频参差、重频抖动、频率捷变、频率分集、脉内调制或调相等新型体制雷达不断取代传统的常规脉冲雷达,使得雷达对抗信号环境越来越复杂多变。对于常规雷达信号而言,PRI是信号分选与识别的一个重要参数。但随着信号环境的密集化和信号调制样式的多样化,用传统的方法已不能对复杂体制雷达信号进行较好分析。文献[1]首先要利用脉冲流提取模板序列,然后再进行威胁雷达信号识别告警。由于识别系统先要提取雷达信号的模板序列,再进行序列匹配识别,这样雷达信号识别过程会比较繁琐,并且识别结果受由于噪声、干扰信号和测量误差会影响较大。文献[2]利用脉冲样本图重新对雷达信号进行描述,但是信号匹配识别过程是进行脉冲匹配,造成系统运算负担重,并且系统对某些复杂体制的雷达信号无法准确识别。针对传统雷达信号识别系统识别过程复杂繁琐、运算量大、对复杂体制的雷达信号识别能力差等问题,本文基于雷达信号的PRI参数对雷达信号分选进行分析,对到达时间(TOA)折叠法雷达信号分选和灰关联分析法进行研究,提出了基于折叠法和灰关联分析的威胁雷达信号识别方法。
1 TOA折叠法
雷达信号分选是雷达对抗信号处理的重要内容之一,也是在复杂战场电磁环境下准确、快速地识别威胁雷达信号的基础。信号分选过程就是从随机交叠的脉冲信号流中分离出各部雷达的单独脉冲列的过程,其利用同一部雷达信号参数的相关性和不同雷达信号参数的差异性来实现[4]。目前,常用的雷达信号分选方法有动态扩展关联法、直方图法、累积差直方图法(CDIF)、顺序差直方图法(SDIF)、PRI变换法、TOA折叠法。动态扩展关联法的优点是原理简单,易于实现,但是运算量较大,且容差的门限值较小,所以对脉冲干扰和脉冲丢失都很敏感。直方图法对任意TOA差值处理,所以运算量大,并且不能消除谐波的影响。为弥补这些不足,专家学者们对直方图法进行改进,其中最重要的有CDIF和SDIF。CDIF对传统直方图算法进行较大改进,它是基于脉冲自相关性的相关函数的改进算法,具有直方图统计和序列搜索的优点。但是CDIF算法的运算量也比较大,PRI的随机抖动可能会导致算法出现严重的错误,且在脉冲丢失数量较大的时候,CDIF将会检测出PRI的子谐波。SDIF算法对不同阶的差值不进行积累,而只检测当前级的差值直方图,也取消了两倍脉冲间隔的直方图值与门限的比较,这样便减少了算法计算量。但是对CDIF算法无法有效地分选新体制雷达信号。PRI变换算法虽能够较好适应复杂体制的雷达信号,很好地抑制了子谐波,但是计算仍较大,对PRI抖动的信号无法正确分选。TOA折叠分选是基于样本库中的威胁雷达信号先验知识,根据信号的TOA信息,通过时域折叠变换的方法,将全脉冲在平面上用图形显示出来,从而分选信号。设截获脉冲流共有N个信号脉冲,第i个脉冲的 TOA为tk,折叠平面的宽度为T0,每个信号脉冲在TOA折叠平面图形上用一个点表示,则平面内的第i个信号脉冲的坐标为(xi,yi):
(1)
式(1)中,Δx为单位时间所对应的x方向上的像素点,Δy为单位时间所对应的y方向上的像素点,mod(·)为取余数操作;int(·)为取整操作。xi,yi分别只与ti除以T0后的余数和商有关。
TOA折叠法信号分选的依据:由于不同雷达信号的PRI长度和PRI调制形式存在差异,所以在对截获脉冲流处理时,可通过改变折叠平面的宽度值T0,将不同PRI长度和不同PRI形式的雷达信号以不同的特征曲线显示出来。
1.1 常规雷达信号的折叠分选
对脉冲重复周期为PRI的常规雷达信号,其第i个信号脉冲的到达时间为
ti=t0+(i-1)·PRI+ε,i=1,2,…,N
(2)
式(2)中,t0为第一个脉冲信号的到达时间,t0 当平面折叠宽度值T0=PRI时, 因此,第i个信号脉冲将出现在第i行Δx·t0处,该信号每个周期内的脉冲在图形中构成一条近似垂直的直线。若平面折叠宽度值T0的取值小于信号脉冲重复周期PRI,则在图形中构成一条斜率为负的直线;若T0的取值大于信号脉冲重复周期PRI,则在图形中构成一条斜率为正的直线。 由于各PRI复杂调制信号的样式和重复周期不同,当平面折叠宽度T0为某种PRI调制信号的重复周期时,该种信号的特征曲线变得明显;平面折叠宽度T0变成另一宽度时,该种PRI调制信号特征曲线变得模糊(或混乱),而另一种PRI调制信号的特征曲线有可能变得清晰。总之,在对平面折叠宽度T0进行调整时可以显示出不同PRI信号的特征曲线。所以对于PRI复杂调制的雷达信号(参差调制、正弦调制、滑变调制等)而言,由于它们在大周期上仍是重复周期信号,TOA折叠分选同样能够显示出信号的PRI特征曲线。 例如某参差变化的复杂信号的TOA折叠用Matlab仿真结果如图1所示。 从图1可知脉冲序列的到达时间点在平面上形成4条斜率很大的曲线,该曲线称为信号的特征曲线,根据图中特征曲线的位置可进一步求出相邻脉冲之间的子间隔。一般情况下,雷达信号脉冲流是周期性变化的,所以我们可以从信号序列中选取一个周期的脉冲序列,作为该模式下的雷达脉冲信号样本模板[5]。而以雷达信号PRI为折叠宽度反映的也是一个周期内信号的特征,所以我们可以用信号的折叠结果进行威胁雷达信号识别。 灰关联分析是灰色系统理论的主要内容之一。它是定性分析和定量分析相结合、社会科学和自然科学相结合的有效工具。目前,灰关联分析理论已经被广泛地应用于各个领域,它的计算复杂度低于多数的统计方法,识别效果却通常能够达到较好的水平[7]。灰关联分析是根据数据列元素之间相似或相异程度来衡量序列的接近程度,为快速、准确地判断TOA折叠聚类后的信号是否为目标威胁雷达信号,本文用信号的子周期或重复间隔作为依据,进行灰关联分析威胁雷达信号识别处理。 1)求信号各子周期值 接收脉冲信号以目标威胁雷达的重复间隔T0为折叠宽度,经过前部分TOA折叠分选后得到的特征曲线能够显示出雷达信号的特征。为能够进一步判断折叠分选后的该信号是否为威胁雷达信号,需求出该信号的各个子周期。 (3) (4) 2)确定参考数列和比较数列 3)求灰关联系数 在进行灰关联分析前,为了消除各序列数据的量纲影响,先对原始数据进行规范化处理。本文采用区间值化法处理数据,按照下式处理得到新的数列。 对原始数据规范化后,绝对差计算公式为:Δij=PRIi′(j)-PRI0′(j) 由此可得PRIi(j)与PRI0(j)的灰关联系数为 (5) 将所得的分辨系数序列ρ(j)=(ρ(1),ρ(2),…,ρ(n-1))带入式(5)中,关联系数的计算公式变成: (6) 由于关联系数结果较多,为便于比较,采用灰关联度这个概念,记为γ(PRI0,PRIi)。计算灰关联度时,由于各个子周期在信号识别中的重要性相同,故分配的权重ωi(j)相同。 4)求各数列的灰关联度 定义第i个比较数列的灰关联度为 (7) 为验证上述的威胁雷达识别法,本文进行仿真实验验证分析。实际环境中,为减小后续信号处理的计算量,提高TOA折叠分选速度及灰关联分析识别的准确度,在进行折叠分选前会先对截获脉冲流进行预分选。雷达信号预分选的目的是降低信号密度,以利于信号分选。可利用脉冲宽度(PW)、载波频率(RF)、脉冲到达方向(DOA)、脉冲幅度(PA)等特征参数与存储器中预存的威胁雷达信号的脉冲特征参数进行匹配相关处理, 将不感兴趣的脉冲进行虑除。 对截获脉冲流进行预分选后,将剩余的脉冲流以威胁雷达信号的脉冲重复周期为平面折叠宽度进行TOA折叠分选处理,最后用灰关联分析法识别威胁雷达信号,基于折叠法和灰关联分析法的威胁雷达信号识别流程框图如图2所示。 图2 信号识别流程框图 仿真实验中截获信号脉冲流包含6部雷达信号,分别为1部PRI固定雷达信号, 1部PRI抖动雷达信号(抖动量δ=10%), 1部三参差雷达信号, 1部滑变信号,PRI滑变范围为100~310 μs;1部正弦调制信号,PRI调制均值PRI0=200 μs;1部PRI脉组捷变雷达信号,详细信息见表1。仿真实验使用的软件为Matlab 7.6.0;硬件设备为酷睿i3,双核,2.3 GHz的计算机一台;仿真系统平台为Windows10系统。 表1 雷达信号参数表Tab.1 Radar signal parameter table 本次仿真实验中采用脉冲宽度、载波频率对截获脉冲流进行预分选,然后分别以各个雷达信号的PRI为折叠宽度T0,进行预分选前后的折叠仿真,并将各个信号的折叠平面宽度增大进行折叠仿真,讨论信号特征曲线变化特征。图3为未经过预分选前对截获脉冲流进行TOA折叠分选的平面图;图4为经过预分选后进行TOA折叠分选的平面图。 从图3的仿真结果图可看出经过TOA折叠法处理后,与折叠平面周期宽度接近或相等的重复周期雷达信号的到达时间点分布比较集中,形成了斜率很大的曲线;而重复周期与折叠平面宽度不相同的到达时间点和噪声点,则是散乱分布在折叠平面内。但是对截获脉冲流未进行预分选就直接进行TOA折叠分选的话,分选结果中会存在相似重复周期的非目标威胁雷达信号的脉冲流,分选结果较为复杂,从而不利于后续对目标威胁雷达信号识别操作。 图4为经过预分选后进行TOA折叠分选的仿真结果图,对比图3与图4可知,经过预分选后的折叠分选结果可较清晰地看到目标威胁雷达的折叠后的特征曲线。从这些特征曲线中,我们可进一步用均值法求出各个相邻特征曲线的间隔时间,即雷达信号的子周期,为后续的灰关联分析提供依据。同时,从图3与图4中同一信号的仿真结果可知,对于不同PRI调制类型的雷达信号,其特征曲线显示效果存在差异。例如对PRI抖动调制信号,由于它的PRI抖动范围较大,形成特征曲线的点较为分散;甚至在未经过预分选的图3中不易找到信号2的特征曲线,而有些非目标雷达信号的特征曲线则较为明显。 下面以各个已知信号的PRI值加上0.1 μs为折叠平面宽度,进行各个信号分选后的折叠仿真,仿真结果如图5所示。由图5可知,折叠平面宽度比威胁雷达信号的PRI大时,信号的特征曲线变成向左倾斜的曲线。这是因为目标威胁雷达信号的到达时间点在折叠平面内的位置随着折叠宽度加大向左移动。同理可知,当折叠平面宽度比威胁雷达信号的PRI小时,信号的到达时间点在折叠平面内的位置随着折叠宽度减小向右移动,而信号特征曲线应该向右倾斜。另外,随着折叠宽度T0值的增大,在T0时间内包含的信号脉冲数量也增加,即信号在折叠平面内显示的曲线数量也会增加。 为验证TOA折叠分选适应复杂环境能力,将仿真实验中雷达信号数量增至60部,包括了前面的6部雷达信号。以信号3为威胁雷达信号,分别运用CDIF法、PRI变换法和TOA折叠法进行分选信号仿真,进行300次MonteCarlo实验结果取平均值得到表2。其中正确分选率为正确分选的实验次数与总实验次数的比值。 CDIF算法由于脉冲丢失可能存在子谐波,分选过程存在参差鉴别的环节,所以正确分选率最低。其中CDIF算法分选在计算到二阶差值直方图时才成功分选出信号,如图6所示。而TOA折叠法利用PRI对脉冲到达时间进行处理,对信号复杂体制适应能力强,方法简单,且无子谐波问题,脉冲丢失对分选影响也较小,所以正确分选率较高。脉冲流经过预分选后的TOA折叠分选结果如图7。 表2 三种方法的仿真结果Tab.2 The simulation results of the three methods 本文采用的灰关联分析法对分辨系数ρ的取值方法进行改进优化,采用了分辨系数序列取值的方法,现对本文中改进灰关联分析法进行验证。实验选重频调制较简单的信号1和较复杂的信号4进行比较,从表3中可知本文中优化后的灰关联分析法对复杂环境的适应能力得到提高。以信号4为目标威胁雷达时的灰关联分析结果如图8。从图8可知,实验得到的灰关联度曲线出现多个峰值,这是因为同一雷达信号的PRI子周期的所有顺序组合中存在相似的顺序组合。根据灰关联度越大,两者越相关的原则,我们将灰关联度最大的作为分析结果。 表3 不同灰关联分析的实验结果Tab.3 Experimental results of different gray relational analysis 本文提出了基于TOA折叠法和灰关联分析的威胁雷达信号识别方法。该方法先用折叠法对预分选后的脉冲流进行分选,然后利用雷达信号特征曲线计算目标雷达信号的子周期,再用改进的灰关联分析法进行威胁雷达信号识别。与传统信号识别方法相比,该方法简单易用,简化了雷达信号处理过程。通过仿真实验表明,本文提出的基于TOA折叠分选法和灰关联分析的威胁雷达信号识别方法是有效可行的,对复杂的电磁环境和复杂体制的雷达信号的适应能力强,识别结果准确度高。 参考文献: [1]马燕.自提取模板序列机载雷达威胁告警算法[J].雷达科学与技术,2014,12(6):639-648. [2]王遵禄,陈婷,罗景青.基于脉冲样本图的雷达辐射源识别方法[J].雷达科学与技术,2009,7(4):284-288. [3]赵闯,赵拥军,李冬海. TOA折叠平面特征点无监督聚类[J].现代雷达,2010,32(1):39-41. [4]王杰贵,靳学明.现代雷达信号分选技术综述[J].雷达科学与技术,2006,4(4):104-120. [5]龚亮亮,罗景青,吴世龙.一种基于模板脉冲序列的雷达辐射源识别方法[J].现代防御技术,2008,36(5):131-134. [6]Staelin D H.Fast folding algorithm for detection of periodic pulse trains[J].Proceedings of the IEEE,1969,57(1):724. [7]陈昊,侯慧群,杨承志,等. 基于改进灰关联的雷达辐射源识别方法研究[J].现代防御技术,2013,4(2):155-159. [8]林云,司锡才,周若琳,等.改进灰色关联算法在辐射源识别中的应用[J].通信学报,2010(8A):166-171.1.2 PRI复杂调制的雷达信号折叠分选
2 灰关联分析法威胁雷达信号识别
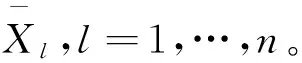
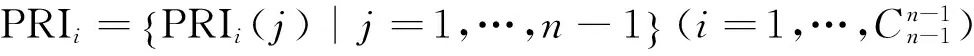
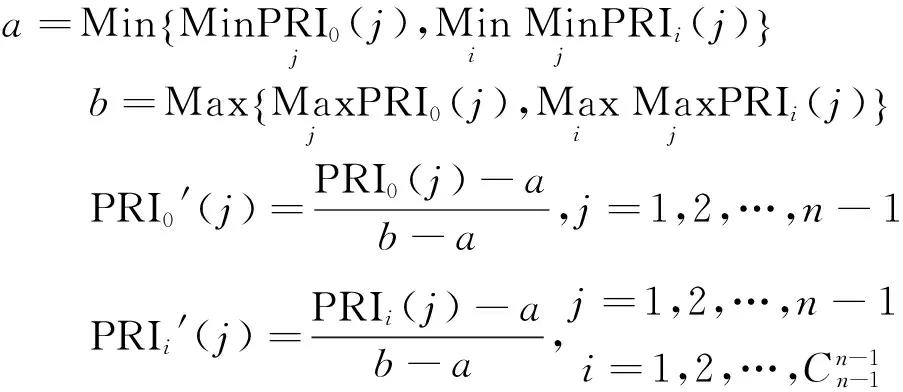
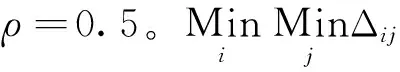
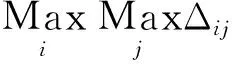

3 仿真分析
Fig.2 Signal identification process block diagram
3.1 TOA折叠分选仿真

3.2 灰关联分析结果分析

4 结论

