基于多频观测量的北斗卫星误差来源与组成检测方法

，， ，，

(1.北京航空航天大学电子信息工程学院，北京 100191；2.北京卫星导航中心，北京 100094)

0 引言

卫星导航系统的定位误差按来源分主要由与卫星有关的误差、与信号传播有关的误差、与接收机有关的误差三部分组成[1]。其中影响定位精度的系统误差(例如星历误差、卫星钟差等)与传播误差(例如电离层延迟误差、对流层延迟误差等)可以通过差分技术或建模得以消除[2]。

传播误差中的多径效应误差可以通过码和载波相位观测量组合来分析，这个组合是关于多径的时间序列的表达式，可以用MP(multipath)值表示[3]。近些年来，大量的研究人员利用北斗卫星导航系统的观测量对其误差进行了深入分析。其中，文献[4]利用三频组合分析了北斗同步卫星观测量的多径误差；文献[5]研究了码多径对信号特性和定位的影响，同时，利用组合观测量的方法还可消除电离层误差；文献[6]中分析了双频组合修正电离层误差方法；文献[7]研究了三频消除电离层误差的方法。有研究表明，北斗卫星导航系统的MEO和IGSO卫星上存在较强的多径误差[8]。考虑到传统的北斗卫星信号有三个频率的观测量，文献[9]研究了组合观测量的特性，文献[10]研究了三频载波相位的整周模糊度解算。文献[11]利用三频点的北斗卫星几何与电离层无关观测量对多径误差进行了分析；但受到传统码-载波观测量数量的限制，对误差的来源分析还不够精确和全面。

随着北斗卫星导航系统建设，2015年北斗试验卫星播发了四个民用频点的导航信号，为分析北斗卫星导航系统的误差来源提供更丰富的观测信息。针对上述问题，本文提出了基于多频观测量的北斗卫星误差来源与组成检测方法。

1 GNSS观测量误差模型

伪距和载波相位是全球卫星导航系统(Global Navigation Satellite System，GNSS)的两个基本距离测量值。导航卫星p的i频点上的载波相位观测量和码观测量，分别表示如下[12]：

(1)

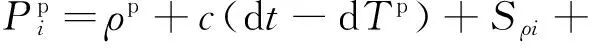
(2)

电离层是一种弥散性介质，其折射率是一个关于电磁波频率f的函数。若考虑二阶及以上电离层延迟分量，可得伪码以m为单位的电离层延时Iρ和载波相位测量值φ的电离层延时Iφ为[13]：

(3)

其中，Iρ为码的电离层延迟，Iφ为载波的电离层延迟，Ai为系数，f为频率。

北斗试验卫星能够提供B1I、B2a、B2b(或B2I)和B3I的四个导航信号[14]，如表1所示。

表1 北斗信号频点Tab.1 The frequencies of BeiDou signal

2 多频点码载波组合的计算

单频的码-载波组合可以表示为：

M1(Pi-Li)=Sφi-Sρi+Iφi-Iρi+
MPi-MLi+λiNi+εi-δi

(4)

三频码-载波组合可以写为：

M3(Pi,Li,Lj,Lk)=c1·Pi+
c2·Li+c3·Lj+c4·Lk

(5)

四个频点的码-载波组合为：

M4(Pi,Li,Lj,Lk,Lz)=c1·Pi+c2·Li+
c3·Lj+c4·Lk+c5·Lz

(6)

在式(4)—式(6)中，Pi，Li，Lj，Lk，Lz分别是同一颗卫星的四个频点信号的码和载波相位；c1,c2,c3,c4,c5为常系数项。

对于单频组合，从式(4)可以看出，误差中包含电离层误差，地面多径误差和星上误差等。对于三频组合方法，为了得到几何无关、对流层无关、一阶电离层无关的观测量，常系数项的取值为：

(7)

对于四频组合方法，为了得到几何无关、对流层无关的观测量、一二阶电离层无关的观测量，常系数项的取值为：

(8)

可分别计算出一组三频和四频观测组合值，如式(9)和式(10)所示：

(9)

(10)

3 BDS卫星测量误差检测与组成分析

为了对BDS定位测量误差组成进行分析，需要在不同地点采集不同频点的北斗试验卫星信号。因此，本文利用中频采集器对楼顶小天线的信号进行了连续采集，覆盖了北斗试验卫星四个频点(B1I，B2a，B2b，B3I)；然后，用北斗软件接收机提取出卫星各个频点的码相位和载波相位，再分别利用单频、三频、四频码-载波组合公式进行处理分析；同时，还对位于北京某地的定向天线进行了三频数据的采集，对比了北斗32号卫星观测量误差，实现了其组成成分的分析。

3.1 小天线单频、三频、四频组合波动情况

对位于楼顶的小天线采用单频码-载波组合方法，可以消除对流层延迟。剩余的误差主要来源于地面多径、一阶电离层误差、二阶电离层误差、星上误差。三频码-载波组合观测量则能够消除一阶电离层误差和对流层延迟。此时，剩余的误差主要来源于地面多径、二阶电离层和星上误差。而采用四频码载波组合方法能够在三频码载波的基础上进一步消除了二阶电离层，此时的误差主要来源于地面多径和星上误差。各组合方法所包含误差情况详见表2。

表2 各频点组合方法包含误差情况对比Tab.2 The comparision of error containd in different combinations

图1(a)、(b)、(c)分别表示小天线采集数据处理的北斗32号星B1I频点的单频、三频、四频码-载波组合波动图；图2(a)、(b)、(c)分别表示小天线采集数据处理的北斗32号星B2b频点的单频、三频、四频码-载波组合波动图；图3(a)、(b)、(c)分别表示小天线采集数据处理的北斗32号星B3I频点的单频、三频、四频码-载波组合波动情况。

3.2 定向天线三频码-载波组合波动情况

定向天线接收信号具有指向性，具有很强的抗干扰能力，其三频码载波组合可以忽略地面多径和电离层误差，误差主要来源于卫星自身的误差，图4表示定向天线采集数据处理的北斗导航32号星B1I、B2I、B3I三个频点的三频载波和三频码载波波动图，横坐标均为采样点，采样频率是25 Hz，纵坐标的单位是m。

定向天线实验数据表明，B1I/B2I/B3I三个频点的码-载波波动分别为0.2 m，0.3 m和0.3 m，误差要远低于之前地面小天线的结果，说明了之前的误差很大程度上来源于地面环境。

3.3 误差组成结果分析

将小天线采集的单频、三频、四频码-载波观测量组合波动和指向性天线的三频MP值波动情况进行对比，如表3所示。

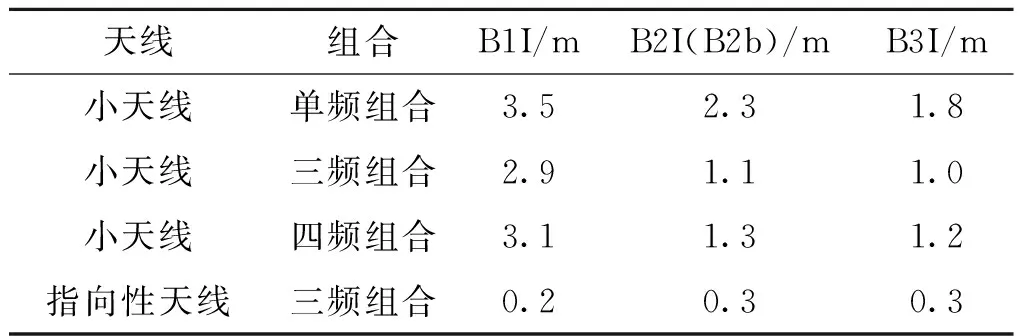
表3 小天线与定向天线B1I、B2I(B2b)、B3I多频码-载波组合波动值Tab.3 The fluctuations of B1I,B2I(B2b),B3I multiple-frequrncy code-carrier combination of the small antenna and directional attenna

三频组合在小天线单频组合的基础上消除了一阶电离层误差，因此二者差值为一阶电离层误差值；小天线四频组合在三频的基础上又消除了二阶电离层误差，因此二者差值即约为二阶电离层误差值；指向性天线的三频组合的波动本身可看作卫星自身信号误差。因此，可以对比分析出B1I、B2I、B3I三频点的电离层误差，地面多径误差和星上误差的值，结果如表4所示。B1I、B2I、B3I三个频点上，各部分的误差组成如图5(a)，(b)，(c)所示。

表4 B1I、B2I(B2b)、B3I三频点上各类误差比例值Tab.4 The proportion of different error on B1I,B2I(B2b),B3I frequency

从图5可以看出，若忽略对流层延迟的影响，B1I、B2I、B3I三个频点上误差来源主要是一阶电离层和地面多径误差，所占比例之和分别是总误差来源的88.5%，78.3%，72.2%；二阶电离层误差和星历误差所占比例为11.5%～27.8%，上述一、二阶电离层误差可以通过多频组合的方式消除。其余的误差主要为星上误差和噪声大约0.2～0.3 m，目前尚没有较好的消除方法，可以在后续开展进一步研究工作。

4 结论

本文提出了基于多频观测量的北斗卫星误差来源与组成检测方法。该方法利用单频、三频和四频码-载波相位的观测量组合，对小天线和定向天线采集数据进行了分析，实现了对北斗电离层、多径、星上误差的检测和分离。测量误差检测与组成结果分析表明，将总误差看作一、二阶电离层，多径误差和星上误差的集合；多径误差和一阶电离层误差约占总误差来源的70%～80%；电离层二阶误差约占总误差的10%左右，可以通过组合观测量的方法进行消除；星上误差和噪声可通过定向天线的码-载波组合波动偏差进行检测，约为0.2～0.3 m, 目前尚没有较好的消除方法。考虑到未来北斗卫星导航系统会继续播发四个频点的信号，多频码-载波组合观测量对导航卫星的不同误差来源进行检测与分离的方法，可推广到未来北斗卫星导航系统的误差检测和评估中。

参考文献:

[1]谢钢.GPS原理与接收机设计[M].北京：电子工业出版社,2014：78-89.

[2]袁赫良,金天,杨茜，等.采用相关曲线偏差的导航卫星多径信号分离方法[J].西安交通大学学报,2017,51(2)：65-71.

[3] Zhang X, Ding L. Quality analysis of the second generation compass observables and stochastic model refining[J].Geomatics and Information Science of Wuhan University,2013,38(7)：832-836.

[4] Wang G, Jong K D, Zhao Q, et al. Multipath analysis of code measurements for BeiDou geostationary satellites[J]. GPS Solutions,2015,19(1)：129-139.

[5] Zhang F, He H, Tang B, et al. Analysis of signal characteristics and positioning performance affected by pseudorange multipath for COMPASS[C]//China Satellite Navigation Conference(CSNC)2013.Wuhan:2013,493-503.

[6] Zhao W, Zhao N, Zhao H, et al. Analysis of the Pseudorange Multipath Impact on Dual-Frequency Ionospheric Delay Correction in Compass System[C]//China Satellite Navigation Conference(CSNC)2013.Wuhan:2013,355-365.

[7] Wang Z, Wu Y, Zhang K, et al. Triple-frequency method for high-order ionospheric refractive error modeling in GPS modernization[J]. Positioning,2005,01(1)：291-295.

[8] Wanninger L, Beer S. BeiDou satellite-induced code pseudorange variations： diagnosis and therapy[J]. GPS Solutions,2014,19(4)：639-648.

[9] Wang G, Jong K D, Li X, et al. Analysis of Characteristics of BDS Observable Combinations for Wide-Lane Integer Ambiguity Resolution[C]// China Satellite Navigation Conference (CSNC) 2014 Proceedings. Berlin Heidelberg: Springer,2014：411-425.

[10]Zhang X, He X. Performance analysis of triple-frequency ambiguity resolution with BeiDou observations[J]. GPS Solutions, 2016, 20(2)：1-13.

[11] Zhao Q, Wang G, Liu Z, et al. Analysis of BeiDou Satellite Measurements with Code Multipath and Geometry-Free Ionosphere-Free Combinations[J]. Sensors, 2016, 16(1)：123.

[12] Wang K, Rothacher M. Ambiguity resolution for triple-frequency geometry-free and ionosphere-free combination tested with real data[J]. Journal of Geodesy,2013,87(6)：539-553.

[13] Feng Y. GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals[J]. Journal of Geodesy,2008,82(12)：847-862.

[14] Feng Y, Li B. A benefit of multiple carrier GNSS signals： Regional scale network-based RTK with doubled inter-station distances[J]. Journal of Spatial Science,2008,53(2)：135-147.