卷积神经网络图像处理
柯研 王希龙 郑钰辉
摘要
随着互联网信息技术的迅速发展,图像类型的数据也呈现出爆炸式增长,如何能够快速有效地对这些图像信息进行处理,已经成为目前计算机领域的一个重要研究方向。传统的图像识别方法,主要是先通过提取一些特征点,然后再通过数学统计模型表示图像,最后通过图像匹配的算法对图像进行识别。然而随着人工智能,深度神经网络的发展,深度学习的技术已经广泛地应用于语音识别,自然语言处理,计算机视觉等多个领域,并且取得了巨大的成功。本文主要介绍一种对于处理图像非常有效的神经网络 卷积神经网络。
【关键词】深度学习 卷积神经網络 图像处理
近年来,随着研究神经网络特别是卷积神经网络相关领域的研究人员不断地增长,技术的发展也是日新月异,卷积神经网络也变的愈加复杂,越来越深。卷积神经网络是人工神经网络和深度学习相结合的结构,所谓深度神经网络或者深度学习指的是含有多层隐藏层的神经网络。目前,卷积神经网络已经成为人工神经网络中应用最广泛,效果最好的一种神经网络。卷积神经网络的大体结构与普通的人工神经网络非常相似,但是在大规模的图像数据集上着有非常好的效果。
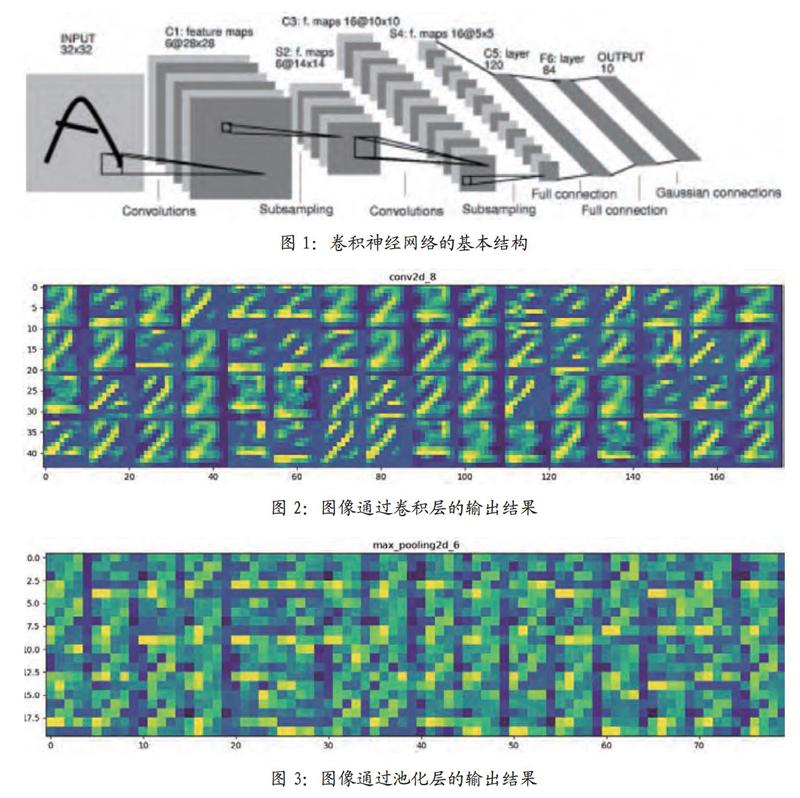
如图1所示,卷积神经网络的主要结构包括;卷积层,池化层以及全连接层。卷积神经网络属于前馈式神经网络,通过卷积,池化以及非线性激活函数映射这些操作一层一层地将高层的语义信息从原始数据中剥离出来,这就属于前馈运算。每个卷积层后都会有一个池化层,这是因为信息此时从低维映射到高维,参数非常多,维度也过高,不适宜作为下一层神经元的输入,所以必须对这一层的输出做一个降维的处理,因此引入池化操作。若是不对数据进行降维,则很容易造成过拟合,甚至导致维数灾难。
1 积神经网络结构
1.1 卷积层
卷积层对应的就是卷积操作,图像以矩阵X的形式输入,在卷积层中就是X与参数矩阵W做卷积操作的过程。其中W就被称作为卷积核,不同的卷积核能够提取到图像中的不同特征,一般而言我们会把很多卷积核拼接在一起运算,这样就可以尽可能多的获取图像中的信息。卷积核的每个元素与被卷积图像对应位置相乘,再求和。通过卷积核的不断移动,我们就有了一个新的图像,这个图像完全由卷积核在各个位置时的乘积求和的结果组成。二维卷积在图像中的效果就是:对图像的每个像素的邻域(邻域的大小就是卷积核的大小)加权求和得到该像素点的输出值,也就是可以使原信号的特征增强,并且降低噪声。
事实上,卷积网络中的卷积核参数是通过反向传播中不断优化训练学出的,除了可以学到类似于横向边缘、纵向边缘的卷积核,还可以学到任意角度边缘甚至检测颜色、纹理这些信息的卷积核。而且这些卷积核全都可以包含在一个足够复杂的深层卷积神经网络中。如图2所示,这是一张图像经过第卷积层之后的结果,与不同的卷积核卷积运算之后的结果也不相同。随着“组合”这些卷积核以及各种操作的进行,图像的信息会逐渐被抽象为具有高层语义的“概念”表示,然后就可以通过这些高层的语义信息进行后续分类这样的操作。
1.2 池化层
通常我们使用的池化操作为最大池化或者平均池化,与之前卷积层里的卷积核不同,池化层参数矩阵里的参数是不需要学习去变化的。实际使用时只需要提前指定好池化的类型、核大小以及池化操作的步长等超参数就不用再改变了。最大池化也就是在每次操作时,将池化核所覆盖的区域中所有值的最大值作为池化结果,平均池化亦然。池化操作后的图像矩阵大小相比于输入的图像矩阵变小了,也就是说池化操作其实就是一个下采样的过程。
如图3所示,这是一张图像经过第池化层之后的结果,我们可以看出相比于卷积层的输出,池化层的输出更加抽象,通过这样的下采样能够很好的保留主要信息,减少计算量。池化层具有以下这些特性:
(l)特征不变性。池化操作能够使模型更加关注特征的存在与否而不是特征所在的具体位置。这样可以很好的提高模型的泛化能力。
(2)特征降维。由于池化操作属于一个下采样的过程,因此能够减少图像矩阵的维数,在更广范围的范围内抽取特征。
(3)在一定程度防止过拟合,更方便优化。
1.3 激活函数
激活函数层又被称为是非线性映射层,也就是说激活函数的能够增加整个网络模型的表达能力即非线性的特性。如果没有激活函数,卷积池化这些线性操作层的堆叠仍然只能起到一个线性映射的作用,无法表达出图像中的一些非线性特征。通常使用的激活函数有sigmoid,tanh和relu。我们选择的激活函数应该具有如下的一些性质:
(1)非线性。我们需要激活函数去帮助网络模型表示出非线性的特征,线性的函数不符合我们的需求。
(2)连续且可微。我们通过反向传播,使用梯度下降法来优化参数,由于需要求梯度,激活函数必须是连续且可微的。
(3)单调性。激活函数是单调增长或下降时,则损失函数则会是一个凸函数,由于凸函数已经被广泛的研究,有很多已有的方法可以利用方便我们去优化。
(4)在原点处近似于线性。权值矩阵的参数初始化为接近0的随机值时,网络里的参数可以更快地学习更新。
1.4 全连接层
全连接层在卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层的操作就是将原始数据映射到一个新的特征空间上,全连接层则是将学习到的特征空间里的特征参数映射到样本的标记空间里。在实际使用中,全连接层可由全局卷积操作来实现,也就是用一个与前一层输出的图像矩阵大小相同的卷积核与前一层的输出做卷积运算,这样就能够将一个矩阵映射为一个数,而多个这样的卷积核组合就可以将前层输出的图像矩阵映射成一个固定长度的特征向量,一般来说,特征向量的长度也就对应分类的类别数。由于这个特征向量里的值是将经过多个卷积层,池化层以及激活函数所获得的图像特征进行高度提纯得到的,所以这个特征向量具有高层的特征信息,也就是包含了输入图像经过各种操作的所有特征的组合信息,这些信息就是图像中最具有特点特征,这样就可以通过这些信息输出图像具体所属类别的概率值来对图像进行分类。
1.5 损失函数
与很多机器学习模型一样,卷积神经网络也通过最小化损失函数来学习模型里的权值参数。损失函数可以体现出网络模型所输出的预测值与真实值之间的不一致程度,输出的函数值是一个非负的值,輸出值越小,那么说明网络的预测值与真实值越接近,也就是说模型的鲁棒性越好。一般在图像分类中我们选择逻辑回归中的softmax函数作为我们的损失函数。
2 总结
随着深度学习越来越火爆,人工智能也离我们越来越近了,卷积神经网络在工业界广泛的应用,使得我们能够越来越方便快捷地处理各种图像信息,而想要更好的使用卷积神经网络这个工具,就需要深刻地理解它每一部分的含义以及作用,只有这样我们才能知道如何调整各种超参数来优化网络,使其效果更好,在此基础上我们还能不断加深网络,让网络获取更多的信息,甚至是在结构上加入我们的创新,去解决各种各样问题,以此来推动神经网络的发展,推动深度学习的发展,让深度学习在更多的领域迸发出活力。
参考文献
[1]LeCun Y, Bottou L, Bengio Y, et al.Gradient-based learning applied todocument recognition [J].
Proceedingsof the IEEE,
1998, 86 (11): 2278- 2324.
[2lGulcehre C,Moczulski M, Denil M, et al.
Noisy activation functions [C]//Internat ional
Conference on MachineLearning. 2016: 3059-3068.
[3] Graves A, Fern a ndez S, Gomez F,et al. Connectionist temporalclassification: labelling unsegmentedsequence data with recurrent neuralnetworks [C]//Proceedings of the 23rdinternational conference on Machinelearning. ACM, 2006: 369-376.

