水轮机引水系统精细化模型参数辨识研究
方日升
(国网福建省电力有限公司电力科学研究院,福州 350007)
传统的水轮机调速建模模型未考虑到引水系统和尾水系统[1]的影响。水轮机效率与导水机构中水力损失[2]息息相关,在精细建模中必须考虑到水力损失的因素。国内外的学者对水轮机精细化模型进行一定的研究。文献[3]提出一种引水系统近似阀门结构的模型,但是忽略水力损失对水轮机出力的影响。文献[4]提出基于非线性微分几何控制理论,给出水轮机精细线性化过程,但是只考虑了混流式水轮机模型,并未考虑其他几类模型的情况,有一定的局限性。文献[5]提出考虑非线性环节的执行机构的精细化模型。
粒子群算法存在着精度较低、容易发散等缺点。文献[6]提出利用重采样的方法对全局最优粒子采取不同的策略,但对于粒子轨迹信息利用不够。文献[7]提出对粒子群参数区域进行划分,通过对粒子轨迹特性的分析,说明了种群进化对粒子轨迹的影响。本文通过粒子轨迹的分析,提出一种改进的粒子群算法,旨在提高粒子群算法的收敛性和精度。
本文通过黑箱辨识[8]与曲线拟合[9]的方法,提出一种水力损失率与开度之间的多次方表达函数,通过Matlab进行仿真,得出导水机构的水力损失表达函数。
1 水轮机引水部件的水力损失模型
水轮机引水部件的水力损失计算不论是对于水轮机性能估计还是水力优化[10]都有着重要的意义,但是其水能流动的复杂性让水力损失的计算[11]变得异常困难。目前的水力损失模型主要存在两个方面的难题:蜗壳蜗形段的损失计算只涉及于直管而未考虑到弯管也存在水力损失;导叶叶栅的损失模型较为复杂,不能做到精细的损失计算。
1.1 蜗壳水力损失的数学表达
蜗壳的水力损失可以分为三部分进行计算:直管部分的摩擦损失△H1;蜗形段的摩擦损失△H2;水流流向座环的收缩损失△H3。
(1)
式中λ——摩擦损失系数;l——直管长度;d——直管直径;V1——直管流速。
蜗形段分为直管和弯管损失两部分,△H21表示蜗形段直管损失,△H22表示蜗形段弯管损失。
△H2=△H21+△H22
(2)
(3)
(4)
式中K,c和F——表示速度矩、蜗壳系数及断面面积,均为φ的函数;ξl,Vl——表示弯道损失系数及断面速度,均为φ的函数。
底座的局部搜索损失△H3。
(5)
式中ξk——局部损失系数;Vrb——径向流速。
1.2 导水机构水力损失的数学表达
导水机构[12]内的水力损失由壁面边界层损失ζW和叶栅尾迹损失ζ1组成。
(6)
(7)
式中 △E——壁面能量损失;γ——流体重量;△El——叶栅栅后局部能量损失。
1.3 水轮机水力损失的数学表达
由蜗壳和导水机构两部分组成的总水力损失ζ可以表示为
ζ=ζs+ζwζl
(8)
由IEEE Working Group所提出的近似阀门的引水系统模型[13]为
(9)
式中ku,kp——比例系数;G——理想导叶开度;QNL——空载流量;Pt——机械功率;P——理想机械功率;PL——空载损耗功率。
在实际运行中,式(9)可以变为式(10):
(10)
在考虑水力损失的情况,式(10)变为式(11):
(11)
式中ξg——水力损失函数。
1.4 混流式、转桨式水轮机的模型
特殊情况下,考虑到混流式、轴流转桨式水轮机含有转轮桨叶,在水轮机运行中,还需要考虑其水力振动特性。在构造总目标函数时,不仅需要考虑水轮机水力损失,还需要考虑水力振动特性。这就需要搭建多目标优化模型[14]。
多目标优化与单目标优化问题存在着本质区别,因此需要将多目标优化问题转换为单目标问题。构建新的损失函数为
(12)
式中ω——权值;fj(x)——单目标的目标函数。
对于式(12),在优化时,第一个分目标函数为水轮机的效率函数η(y),即(1-ξg)。第二个分目标函数为尾水管水力振动函数a(y),a表示尾水管振动值。对于效率函数而言,值越大越好,而对于尾水管振动函数而言,值越小越好,则为了构建单一的目标函数,将式设计为
ζg=ω1η(y)+ω2[C-a(y)]
(13)
式中ω1,ω2——权重系数;C——一个较大的常数,根据尾水管水力振动测试数据确定。
1.5 水力损失函数的精细化模型
分析表明水力损失与导叶开度的关系比较复杂,很难得到准确表达式,因此通过黑箱原理与曲线拟合的方式,得到一种水力损失与导叶开度的关系:
(14)
水力损失模型定阶流程图如图1所示。

图1 水力损失模型定阶流程图
2 改进型粒子群算法
在传统的粒子群算法[15]中,粒子i在每次迭代过程中有以下信息:
(15)
pi为个体历史最优位置,pg为群体最优位置,vi为粒子当前速度,xi为粒子更新速度。
在任意t+1时刻,PSO迭代按照式(16)、式(17)进行更新:
vid(t+1)=wvid(t)+c1r1(t)(pid(t)-xid(t))+c2r2(t)(pgd(t)-xid(t))
(16)
xid(t+1)=xid(t)+vid(t+1)
(17)
式中ω——惯性权值;c1、c2——学习因子;r1、r2——[0,1]的随机数。
在传统PSO中,算法到了后期收敛性较差,并且容易陷入局部最优。
从表2可以看出,单株净菜CR民喜最重,达到4.9千克,CR春皇后次之,CR黄芯F1最轻,只有2.9千克。净菜率方面,CR民喜最高,达到87%,CR皇春3号最低,为79%。参试品种中,亩产在5836.25~10185.09千克之间,其中CR民喜最高,比CK增产64.5%,CR皇春3号最低,比CK减产5.7%。
针对PSO算法中的不足,通过对粒子轨迹特征的研究与自适应步长的引入,使得粒子在算法前期有较大的步长并向全局最优靠近,在算法后期粒子较小的步长防止粒子振荡并且提高自身的搜索能力,使算法快速收敛。
2.1 自适应步长
通过自适应调整步长已达到算法前期步长大,后期步长小的要求:
(18)
式中step——步长;a——衰减因子;gen——当前代数;gen.max——最大代数。
则速度vi为
vi(t+1)=vi(t)-a(vmax-vmin)
(19)
2.2 粒子轨迹分析
PSO中,ω、c1、c2这三个参数取值对于粒子在迭代过程中的行为影响很大,算法性能也会因三个参数的变化而发生改变。
由文献[16]可以得到不同参数下的闭环极点λ1、λ2:
(20)
(21)
分别从速度与位置的更新可以得到Z变换下的特征方程:
z2+z(φ1+φ2-ω-1)+ω=0
(22)
(z2+z(φ1+φ2-ω-1)+ω)(z-1)=0
(23)

(24)
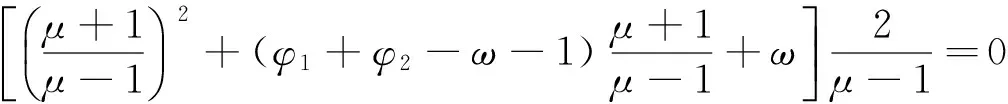
(25)
由Routh判据可知,系统稳定时系数均为正值,则
(26)
在文献[17]中得到的约束条件设置参数如下:
ω≈0.729,c1=c2≈1.494 45
这组参数被用于很多实例当中,均取得了不错的效果。
通过对粒子运行和速度轨迹的分析,当参数满足式(26)的情况下,对参数做进一步优化。对于式(23)中方程的特征根如下:
(27)
为了满足式(26),则根均在负半平面,对于式(23)存在振荡的阻尼系数:
(28)
考虑到ξ与参数ω、c1、c2之间的关系,并且阻尼ξ越小,振幅幅值越大,则可知若ω增大则ξ减小;c1+c2增大,ξ减小。
若pi和pg变化,则粒子运动的中心发生改变,即为粒子的状态在不断变化,而粒子的运动行为依然由ω、c1、c2这三个参数决定。
对参数ω、c1、c2做一下变换:
(29)
做如此变换后,ω由大变小,保证了前期粒子的多样性,后期阻尼变大,则系统振荡幅值变小,确保了系统最后收敛。c1由大变小,丰富了个体前期的多样性,不会过早收敛,后期向全局最优靠近。c2由小变大,使得粒子前期更依赖于自身的寻优,不会陷入过早的收敛状态。c1+c2且不断变小,也从一定角度上减小了系统后期的振荡。
2.3 算法改进效果验证
选用Schaffer函数对PSO与改进PSO进行性能比对[17-19],见表1,求函数的最大值:

(30)
分别对两种算法各进行30次。

表1 PSO与改进PSO算法性能对比
由表1可见,改进PSO算法最优解以及最优解次数均优于PSO算法,通过粒子轨迹以及自适应步长的改进方法可以有效地克服粒子陷入局部最优的问题。
3 算例分析
对某电厂水轮机模型进行辨识,水轮机型号为GZTF07B-WP-560,额定水头为9.3 m,额定出力为21.875 MW,额定转速为93.75 r/min,额定流量为255.86 m3/s。选取60组并网运行数据进行辨识。
目标函数为
(31)
式中p(t)——实际输出;p1(t)——仿真输出。
按图1的流程对函数进行辨识,辨识结果n=3,m=2,ω1=0.7,ω2=0.3。则模型为
ζg=0.7(a3y3+a2y2+a1y+a0)+0.3[C-(b2y2+b1yi1+b0)]
(32)
则代入式(25):

(33)
则待辨识的参数有[kup,kpQNL,a0,a1,a2,a3,C,b2,b1,b0]。辨识结果如表2所示。

表2 模型参数辨识结果
由表2可以看出,在考虑到损失的情况下,目标函数总体的均方差较小,更能反应出水轮机并网的输入输出特性。考虑水力损失的输出波形对比见图2。

图2 考虑水力损失的输出波形对比
由此电厂水轮机运行规程可以查得,最大水头11.9 m和最小水头4.7 m范围内,水轮机以额定转速负荷在相应水头下的出力60%~100%的范围内稳定运行。由图2可以看出,13.5 MW以下的仿真波形与实际差别较大,符合此电厂水轮机的运行规程。
考虑水力损失与未考虑水力损失的仿真波形对比见图3。
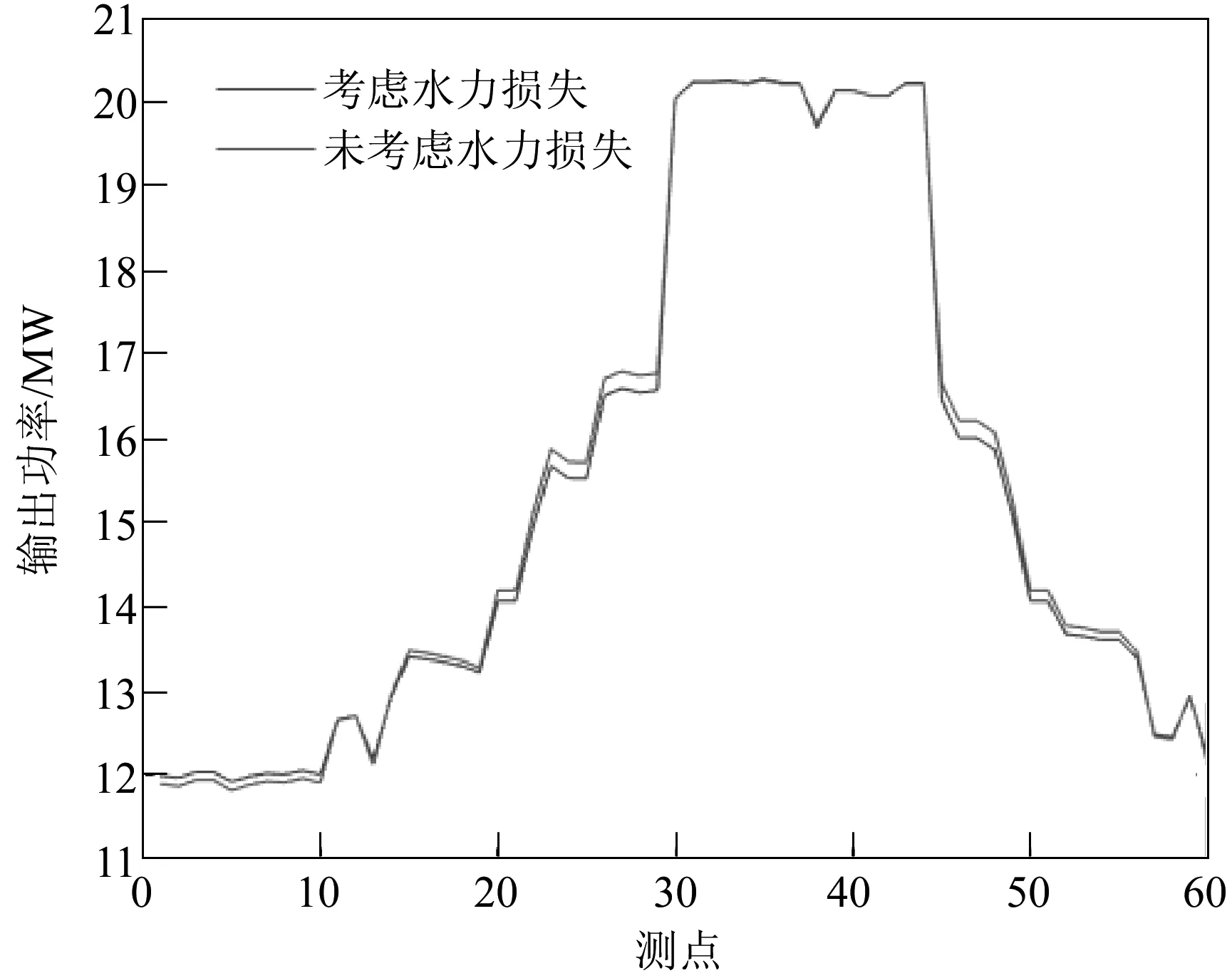
图3 考虑水力损失与未考虑水力损失的仿真波形对比
由图3可以看出,在未考虑水力损失的模型仿真图中总体会比考虑水力损失的模型仿真图稍大,这是因为水力损失在水轮机并网运行当中损耗了部分的能量,若不考虑损失,则不能很好地体现出水轮机并网运行的输入输出特性。
4 结语
本文考虑了水轮机并网运行时,水轮机内部存在水力损失,提出了一种精细化的水轮机阀门模型,并且考虑到混流式、轴流式水轮机存在水力振动,提出了通过多目标函数模型来精细化水力损失函数。结合了改进型粒子群算法进行模型辨识,通过自适应与根轨迹分析来提高粒子群算法的收敛性与精度。考虑水力损失的水轮机模型有很高的精度,通过仿真验证了模型的可行性。
参考文献:
[1] 任兴普, 袁端. 马马崖一级水电站引水与尾水系统布置设计[J]. 水电勘测设计, 2012(2): 16-18.
REN Xingpu, YUAN Duan. Design of diversion Mamaya-1 hydropower project[J].Shuidian Kance Sheji,2012(2):16-18.
[2]刘利娜. 水轮机水力振动的故障诊断[D]. 武汉:华中科技大学, 2003.
[3]UNKNOWN. Hydraulic turbine and turbine control models for system dynamic studies[J]. IEEE Transactions on Power Systems, 1992(1): 167-179.
[4]陈倩, 李全国. 水轮机模型的精确线性化[J]. 科学技术与工程, 2012, 12(14): 3344-3350.
CHEN Qian, LI Quanguo.The accurate linearization of the hydraulic turbine model[J].Science Technology and Engineering,2012,12(14):3344-3350.
[5]黄兴, 严畅, 范伟捷, 等. 水轮机随动系统仿真模型的精细化研究[J]. 水电能源科学, 2016, 34(10): 165-168.
HUANG Xing, YAN Chang, FAn Weijie, et al. Research of turbine servo system simulation model[J].Water Resources and Power,2016. 34(10):165-168.
[6]韩雪, 程奇峰, 赵婷婷, 等. 基于粒子滤波重采样与变异操作的改进粒子群算法[J]. 计算机应用, 2016, 36(4): 1008-1014.
[7]麻荣永, 杨磊磊, 张智超. 基于粒子迭代位移和轨迹的粒子群算法C1、C2参数特性分析[J]. 数学计算(中英文版), 2013(4): 109-115.
MA Rongyong, YANG Leilei, ZHANG Zhichao. Analysis the characteristic of C1, C2based on the PSO of iterative shift and trajectory of particle[J].Mathematical Computation,2013(4):109-115.
[8]赵子都. 黑箱 灰箱和白箱方法:系统辨识的理论基础[J]. 知识工程, 1992(2): 7-10.
[9]刘霞, 王运锋. 基于最小二乘法的自动分段多项式曲线拟合方法研究[J]. 科学技术与工程, 2014, 14(3): 55-58.
LIU Xi, WANG Yunfeng, LIU Yu. Research of automatically piecewise polynomial curve-fitting method based on least-square principle[J].Science Technology and Engineering,2014,14(3): 55-58.
[10]于润桥. 水力参数优化设计方法[J]. 石油钻采工艺, 1988, 10(1): 19-25.
[11]张文倬. 水力学沿程水头损失算式浅析[J]. 四川水利, 2000, 21(1): 46-48.
[12]廖伟丽, 李建. 水轮机导水机构力特性的数值实验研究[J]. 水力发电学报, 2002(4): 100-107.
LIAO Weili, LI Jianzhong. Numerical modeling and flow analysis of the diversion components and entire tandem cascade of hydraulic turbine[J].Journal of Hydroelectric Engineering,2002(4):100-107.
[13] PRABHA, KUMDUR. Power system stability and control: EPRI电力系统工程丛书[M]. 北京:中国电力出版社, 2001.
[14]梁志飞, 夏清, 许洪强, 等. 基于多目标优化模型的省级电网月度发电计划[J]. 电网技术, 2009, 33(13): 90-95.
LIANG Zhifei, XIA Qing, XU Hongqiang, et al. Monthly generation scheduling method based on multi-objective optimization model for provincial power grid[J]. Power System Technology,2009,33(13):90-95.
[15]马金玲, 唐普英. 一种新的改进粒子群算法研究[D].成都:电力科技大学,2007.
[16]韩璞, 孟丽, 王彪, 等. 粒子群算法中粒子轨迹特性研究[J]. 计算机仿真, 2015, 32(12): 235-240.
HAN Pu, MENG Li, WANG Biao, et al. Characteristics of Particle Trajectory in Particle Swarm Optimization[J].Computer Simulation,2015,32(12):235-240.
[17]石永生, 陈家琪. 一种改进的粒子群算法[J]. 河南科技, 2010(11): 50-51.

