基于小波变换的电能质量检测与分析

肖思丽，胡 洁，李建宁

(国网上海市电力公司青浦供电公司，上海 201799)

随着科学技术的不断发展，大量的电力电子设备在工业中得到了广泛应用，这些非线性元件对电网产生冲击性和不平衡性，引起了电能质量扰动问题，对电网电压造成严重波动和影响。如何解决扰动问题是电网急需解决的问题，而改善电能质量必须要找出问题所在，所以快速有效地检测电能质量扰动问题显得尤为重要[1-2]。

在分析电能质量问题中，傅里叶变换作为一种全局性的变化，窗口大小一旦选定就固定了，在非线性领域，具有一定的局限性。而小波变换是一种十分有效地时-频域分析工具，窗口的大小可以根据信号的频率高低自动调节，对信号进行多尺度分析，再利用小波变换的模极大值理论检测突变点发生时刻以及所产生的电压幅值，特别适合于突变信号和不平稳信号的分析[3-4]。

利用db4小波变换的方法对电力系统中存在的五种暂态电能质量扰动问题(电压间断、电压骤降、电压骤升、振荡暂态、脉冲暂态)进行检测与分析，并采用了基于模极大值的奇异点检测方法，从而快速提取扰动信号特征量，判断扰动类型。Matlab仿真结果的正确性和有效性，说明了该方法的可行性，为更快速精准地检测电能质量问题提供保障。在此基础上，本文提出基于小波变换的电能质量检测与分析的研究方法。

1 小波变换方法

1.1 小波变换

小波变换是一种时频局部化分析方法，即可以改变时间窗口和频率窗口对信号进行多维度分析。该算法的时间和频率分辨率随着频率的改变而变化，时间分辨率和频率成正比，频率分辨率和频率成反比[5-6]。

假定平方后在无穷区间都有界，且满足积分条件，并且傅里叶变换满足以下条件：

(1)

则称Ψ(t)为小波变化的母函数或者说是基本小波，并简称小波函数。

将任意二维空间S(R)中的函数q(t)基于小波函数进行一串的小波变换(Continaous Wavelet Transform，简称CWT)，可以用下式表示：

(2)

式中R——实数集；a——伸缩因子；b——平移因子；Wq(a，b)——小波变换系数；q(t)——被变换函数。

1.2 离散变换

当a，b连续变换时，CWT系数具有较大的冗余量，所以连续小波需要离散化。

这一离散化是针对连续的伸缩因子a和连续的平移因子b，并不是时间，用以消除变换中的冗余。

(3)

离散化小波变换系数表示为

(4)

其重构公式为

(5)

其中，c为常数。在低频时，小波变换时间分辨率较低，频率分辨率较高；在高频时，频率分辨率较低，时间分辨率较高。

1.3 Mallat快速算法

S．Mallat提出了一种基于计算离散栅格上小波变换的多分辨(多尺度)分析的快速小波算法——Mallat算法[7-8]。

该算法优势在于可以通过滤波器系数对各类信号进行快速分解和重构，而不需要知道相关小波函数和尺度函数等的具体结构。因此，可以利用该算法对电能质量扰动信号进行相应地检测和提取。

信号q(t)的多分辨率分解公式可以表示为

q(t)=∑k∈Zcj，kφj，k(t)+∑k∈Zdj，kψj，k(t)

(6)

式中cj，k——尺度系数；dj，k——小波系数。

多分辨分析将小波变换的多分辨率特性推广到了空间上的描述，从而印证了构建正交小波基的数学方法。通过对正交小波基的快速算法，进而得出了Mallat算法。多分辨率分析树形图如图1所示。

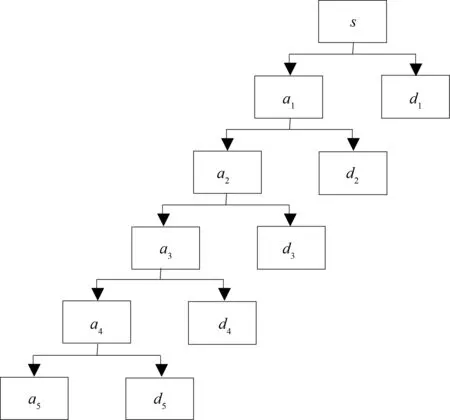
图1 多分辨率分析树形图

s=a5+d1+d2+d3+d4+d5

(7)

s为原始信号，a5是第五尺度上的低频分量，d1、d2、d3、d4、d5是相应尺度上的高频分量。

1.4 模极大值

通常信号在发生突变时，经过多尺度分析的小波变换后的系数可以取到模极大值，根据取得的模极大值进行分析，即可确定扰动信号发生的时间。一般突变点可以清晰地从d1和d2层高频系数中观察出。

为了让小波母函数能在频域和时域都能获得良好的局部特性，通常选取具有紧支性和正则性的函数作为小波母函数，紧支性表示时域的局部性，正则性表示频域的局部性。设K(t)为具有低通平滑作用的滤波函数，满足条件式(8)，并且具有二次可导性。

(8)

(9)

由Fourier变换的微分原理，ε1(t)和ε2(t)满足可容许性条件，即：

(10)

因此，ε1(t)和ε2(t)可作为小波函数。两个对应的小波变换如下：

WTx(τ)ε1(t，α)=x(τ)*ε1(t，a)

(11)

WTx(τ)ε2(t，α)=x(τ)*ε2(t，a)

(12)

WTx(τ)ε1(t，α)是信号x(τ)在尺度a下由K(t)平滑后的一阶导数，其极值点对应的是x(t)函数的突变点，此时为模极大值。WTx(τ)ε2(t，a)是信号x(τ)的二阶导数，二阶导数的过零点对应一阶导数的极值点，通过检测模极大值就可以准确判断信号突变点，从而对电能质量扰动信号突变实时进行定位检测。

中医制剂是医院院内专家经过长期临床实践、临床疗效较好的固定处方自制成药，是体现每家医院自身特色的重要组成部分。随着政府对中医的日渐重视和扶持，中医制剂得到了更大的发展空间，医院对于制剂的财务管理也需要同步跟进，这主要包括相应配套的成本、价格、收支、物资核算与管理财务管理支撑。本文拟在对中医制剂生产特点分析的基础上，阐述医院制剂财务管理实践中的成本核算、价格制定等环节处理方法。

2 扰动信号的提取

Daubechies小波函数(DBN)具有紧支性、正交性和消失矩的特点，针对突变的电能质量扰动信号有较好的灵敏性。在DBN系列小波中，db4小波在时域特性和频域特性两者上都能有很好的兼顾性能，能够较强捕捉扰动的信号。因此，采取db4小波对五种暂态电能质量扰动(电压间断、电压骤降、电压骤升、振荡暂态、脉冲暂态)进行检测分析。

对以下特征量进行提取。

(1)时间特征量。设扰动持续时间为Tdis，t2为扰动结束时间，t1为扰动开始时间。

Tdis=t2-t1

(13)

(2)电压幅值特征量。在扰动持续时间内的电压有效值称为扰动电压幅值，电压幅值的大小是暂态扰动的重要参数，IEEE1159定义的暂态扰动电压幅值变化范围如表1所示。

表1 暂态扰动电压幅值变化参数

(3)电压变化率绝对值。电压变化率作为暂态扰动的一个重要特征量，对于平缓的电压扰动，电压变换率的绝对值较小，而对于急剧的电压扰动，电压变换率的绝对值较大。电压变化率绝对值为

(14)

式中 Δt——采样间隔；Δu——扰动电压变化值。

(4)扰动频率。扰动频率是相邻两次扰动间隔时间的倒数，对于电压波动，扰动的频率比较小，而对于暂态扰动，扰动的频率通常较大。

对于暂态脉冲来说，不存在扰动频率，因此通过该特征量可以很好地辨别稳态、暂态扰动以及暂态扰动中的振荡情况和脉冲情况。扰动频率特征量为

(15)

式中t2，t1——两次相邻扰动的时刻。

3 暂态电能质量的Matlab仿真分析

在电能质量分析中，暂态电能质量干扰包括电压间断、电压骤降、电压骤升、振荡暂态、脉冲暂态等。对5种电能质量现象建立扰动信号数学模型，并运用小波变换的db4小波分析。

3.1 电压间断

电压间断指的是短时间内系统工频电压下降到0.1(标么值)以下，持续时间不到60 s的电磁扰动现象。其数学模型如下：

(16)

图2模拟的是电压间断的波形图，t1为扰动的起止时刻，t2为扰动的结束时刻。其中，ω=2π*50 rad/s，t1=0.04 s，t2=0.11 s，α=0，ψ=0。

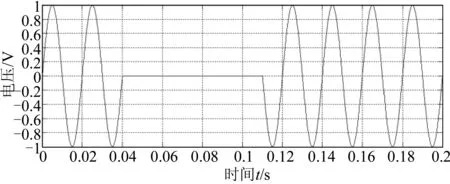
图2 电压间断波形

为了更好地分析电压间断现象，采用db4小波对该扰动信号进行5层分析，如图3所示。

图3 小波变换分析电压间断信号

图3中，α5是经过多频率分析得到的低频系数，反应了原始电压间断信号波形，根据小波变换突变点多检测原理，d1和d2是信号经过小波变换得到的第一层和第二层高频系数，图形中出现较大变化的时刻是模极大值出现的时刻，也是原始电压间断信号的开始与终止时刻。从图3中可以看出，电压间断开始于采样点400，并于采样点1 100结束。

3.2 电压骤降

电压骤降指的是暂时的电压下降，持续时间在半个周波到60 s，幅值在正常值的0.1～0.9(标么值)。其数学模型如下：

(17)

图4模拟的是电压骤降的波形图，t1为扰动的起止时刻，t2为扰动的结束时刻，其中，ω=2π*50 rad/s，t1=0.03 s，t2=0.12 s，α=0.9，ψ=0。

图4 电压骤降波形图

为了更好地分析电压骤降现象，采用db4小波对该扰动信号进行5层分析，如图5所示。

图5 小波变换分析电压骤降信号

从图5中可以看出，在采样点300和采样点1 200处出现了小波变换的模极大值，可以精确地判断出电压骤降点和恢复正常的时间点，电压骤降持续时间为0.09 s，骤降幅值至0.9。

3.3 电压骤升

电压骤升指的是短时间内电压的迅速升高，比如工频电压的有效值增到1.1～1.4(标么值) ，并且持续时间在0.01 ～60 s 的一种电磁扰动现象。其数学模型如下：

(18)

图6模拟的是电压骤升的波形图，t1为扰动的起止时刻，t2为扰动的结束时刻。其中，ω=2π*50 rad/s，t1=0.02 s，t2=0.1 s，α=1.3，ψ=0。

图6 电压骤升波形图

采用db4小波对该扰动信号进行5层分析，如图7所示。

图7 小波变换分析电压骤升信号

从图7中可以看出，利用小波分析可以精确地检测出电压骤升采样点200和电压恢复正常采样点1 000。实现扰动时间精准定位，骤升幅值至1.3(标么值)。

3.4 振荡暂态

振荡暂态是指系统电压在稳定的工作条件下发生突变。

(19)

图8模拟的是振荡暂态的波形图，t1为扰动的起止时刻，t2为扰动的结束时刻。其中，ω=2π*50 rad/s，A=1，An=1，λ=80，n=14，ψ=0，t1=0.03 s，t2=0.1 s。

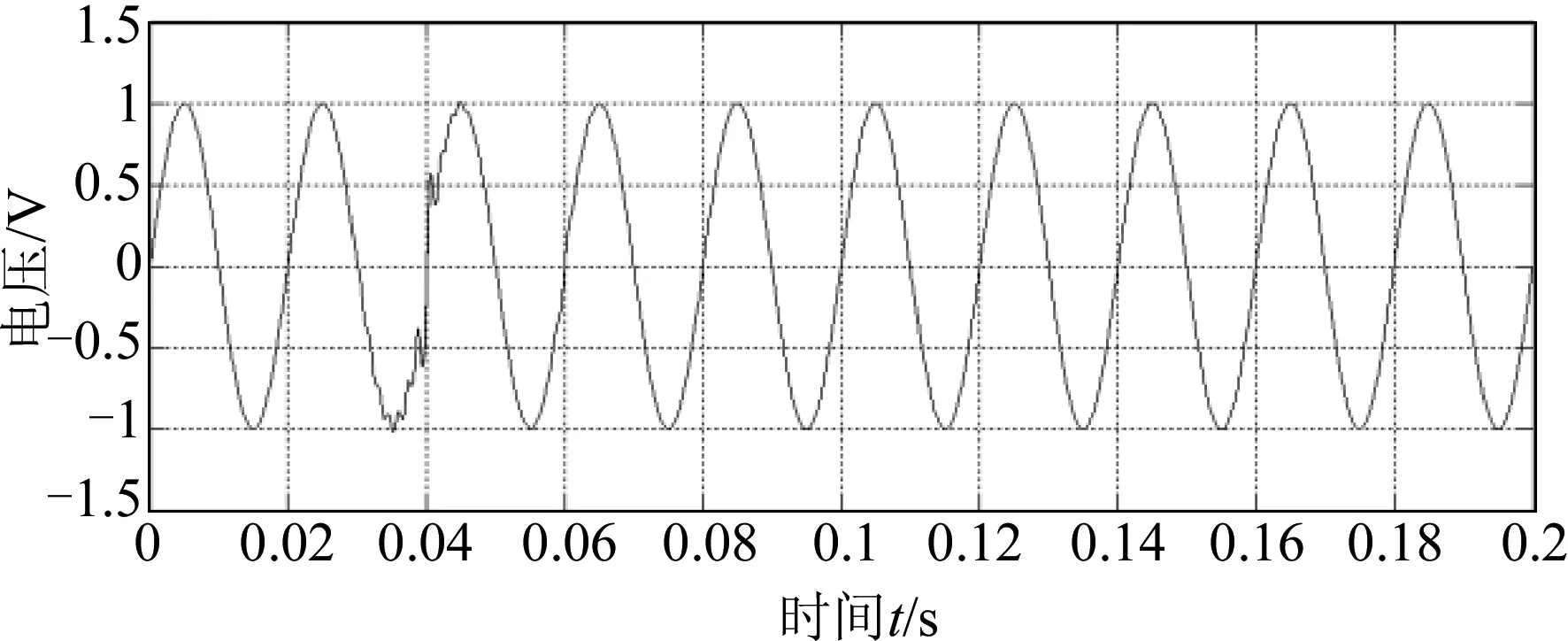
图8 振荡暂态波形图

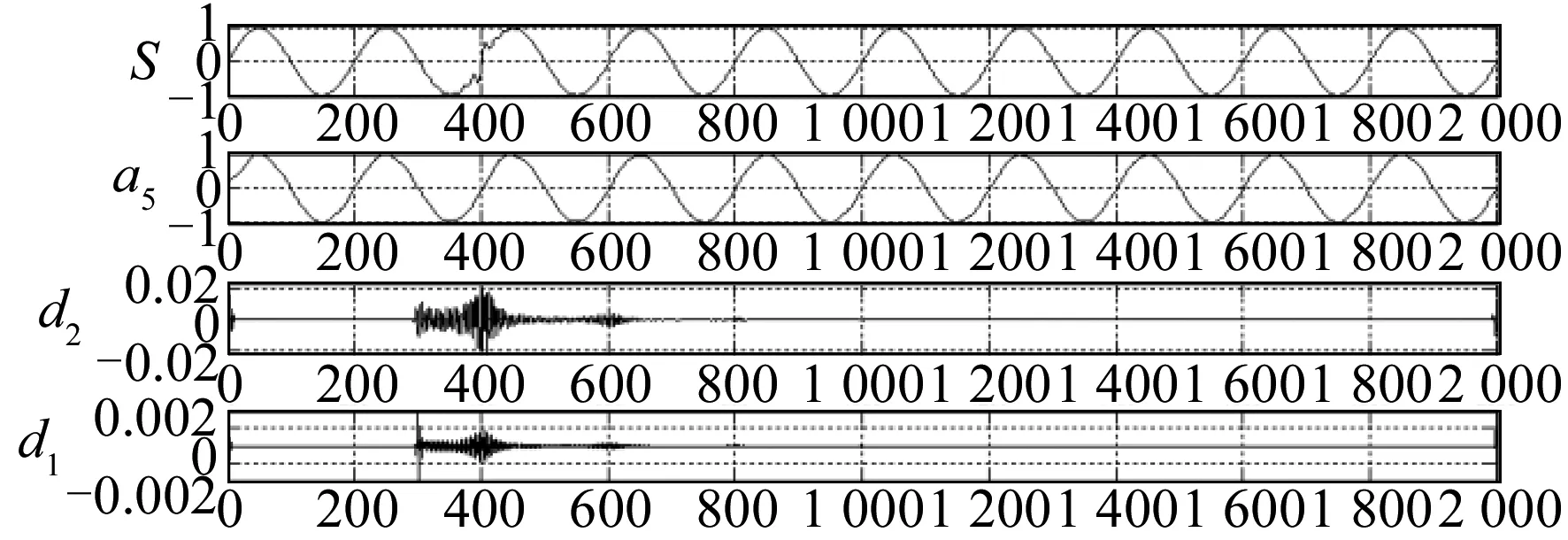
图9 小波变换分析振荡暂态信号

采用db4小波对振荡暂态进行检测分析，如图9所示。由图9可以得出，振荡暂态发生干扰的时刻为采样点300处，实现了扰动精准定位。

3.5 脉冲暂态

模拟含电磁暂态干扰的原始信号，其数学表达式可以表示如下：

(20)

图10模拟的是脉冲暂态的波形图，t1为扰动的起止时刻，t2为扰动的结束时刻。其中，ω=2π*50 rad/s，t1=0.021 s，t2=0.022 s。

图10 脉冲暂态波形图

采用db4小波对脉冲暂态进行检测分析，如图11所示。α5是信号进行小波变换后得到的低频系数，其波形和原来的波形基本一致无变化。d1和d2反应了高频信号的变化情况，在采样点210点处，d1和d2都出现了模极大值的情况，可以清楚地判断出脉冲暂态发生干扰的时刻。

图11 小波变换分析脉冲暂态信号

4 结语

针对暂态电能质量扰动的问题，本文提出了基于小波变换的电能质量检测与分析的方法。利用小波快速分解与重构的特性，使其能够快速分离高频次和低频次小波，从而检测和提取电能质量扰动信号。采用db4小波变换，在Matlab仿真环境下对电压间断、电压骤降、电压骤升、振荡暂态、脉冲暂态这五种现象进行仿真分析，根据小波变换上奇异点对应的模极大值可以精确地定位扰动信号发生结束时刻、持续时间以及幅值大小。通过仿真证明了此方法能够有效精准地检测电能质量扰动。

参考文献：

[1] 于东民. 小波变换在电力系统谐波检测中的应用 [J].科学时代，2014(18)：53-58.

[2]吴军基，刘皓明，孟绍良，等. 小波滤波器在电力系统谐波检测中的应用[J].电力系统及其自动化学报,1999(5):50-54 .

WU Junji, LIU Haoming, MENG Shaoliang, et al. Application of wavelet filter in harmonic wave detection of power system[J]. Proceedings of the CSU-EPSA,1999(5):50-54 .

[3]彭玉华.小波变换与工程应用[M].北京:科学出版社，1999.

[4]段虎，李益华 .小波变换在电力系统谐波检测方面的应用[J].国外电子测量技术，2010 (12) :73-75.

DUAN Hu, LI Yihua. Application of wavelet transform to harmonics detection in power systems[J]. Foreign Electronic Measurement Technology,2010(12):73-75.

[5]谭平.基于小波变换的电能质量扰动检测与定位[J].电工电气，2010(6)：04-07.

TAN Ping. Detection and location of power quality disturbances using wavelet transform[J]. Electrotechnics Electric(Jiangsu Electrical Apparatus)，2010(6)：04-07．

[6]李建平,唐远炎.小波分析方法的应用[M].武汉：华中理工大学出版社，1999.

[7]MALLAT S G.A theory for multi-resolution signal decomposition : the wavelet representation[J]. IEEE Trans on Pattern Analysis and Machine Intelligence，11(7):674-693.

[8]B ZHANG， J SUN. A Power Quality Analysis Method Based on Mallat Algorithm and Fast Fourier Transform[J]. Power System Technology，2007，31(19) :35-40.