基于联合波叠加法的浅海信道下圆柱壳声辐射研究∗
商德江1)2) 钱治文1)2) 何元安3) 肖妍1)2)
1)(哈尔滨工程大学,水声技术重点实验室,哈尔滨 150001)
2)(哈尔滨工程大学水声工程学院,哈尔滨 150001)
3)(中国船舶工业系统工程研究院,北京 100036)
(2017年9月4日收到;2018年1月29日收到修改稿)
1 引 言
我国领海大多属于水深小于200 m的典型浅海环境,潜器结构在浅海所处的声场环境并非自由场,存在水面和水底的反射、散射[1].研究潜器结构在浅海信道下的声辐射,对开展潜器的结构振动辐射噪声实时预报和有效控制具有重要的理论和应用价值,将是以后我国水声技术领域长期关注的热点和难点问题之一.
为了有效研究复杂弹性结构的声辐射问题,Koopmann等[2]提出了利用基于虚拟源代替的波叠加方法进行辐射体的辐射声场等效.文献[3—5]从波叠加法稳定性及计算精度进行了分析,发现波叠加法不仅避免了各阶奇异性处理,且声场计算效率高.波叠加方法以适应性强和计算效率高的优势逐步成为一种研究弹性结构声辐射行之有效的新方法,近年来受到了国内学者极大的关注.应用波叠加法可进行复杂结构的声场重构[6,7],其精度的提高在于等效虚拟源配置的优化.熊济时等[8]采用了三维空间法与波叠加法相结合的方法,对自由场下结构辐射声场精度的影响因素进行了分析;李加庆等[9]和陈鸿洋等[10]分别对结构等效源进行了优化配置,对结构近场声辐射特性进行了研究;在此基础上,詹国强等[11]采用波叠加法获得了结构辐射阻抗矩阵,进而有效分析了复杂水下航行器结构的声辐射模态.通过调整格林函数,部分学者借鉴自由场的波叠加法,对半自由场下的结构等效声场进行了研究分析[12−14].
综上可看出,目前对于水下弹性结构辐射声场特性的研究主要集中于自由场和半空间流体环境下近场声学问题,对浅海信道环境下受多边界影响作用的结构声辐射问题的研究尚不多见.因为传统边界元法、有限元法和统计能量法将严重受限于频率、结构尺寸和信道复杂边界等因素,无法开展研究工作;解析解法一般针对简单二维结构在简单浅海信道下的声场问题[15−17].而浅海环境下声场问题一般针对点源的声传播研究,国内学者很早就进行了这方面的深入研究[18−20],并提出了多种有效的研究方法,但很少针对有限长结构声源在浅海环境下的声场传播问题.为此,在海洋声传播模型的研究基础之上,也有部分学者为了避免复杂结构和浅海环境的多物理场理论推导问题,直接忽略结构与流体、结构与环境的耦合作用,把结构视为点声源,但这样直接忽略了结构的近场声辐射特性,其结构在远程的声场特性的可靠性也待商榷.因此,有学者指出浅海信道中结构的声辐射暂未较好地解决,但它对浅海中水下结构声辐射预报、声学测量和声源识别的研究有极为重要的意义,需要探索一种新的研究方法来解决浅海信道中结构声辐射问题[21].为了有效解决浅海环境下结构声辐射研究过程中所涉及的海底复杂、物理场耦合众多和准确物理模型难以建立等问题,本文通过联合多物理耦合有限元法、信道声传输函数和波叠加法提出了浅海下有限长弹性结构声辐射快速预报方法,即联合波叠加法,并从声辐射源、流体环境影响和声辐射测量的角度进行浅海信道环境下弹性结构辐射声场特性研究分析.
2 理论模型
2.1 信道传输函数
考虑浅海信道下简谐点源声场的圆柱对称性,以通过点源垂直向下为z轴,垂直于z轴的方向为r轴,在均质理想流体中满足的非齐次的亥姆霍兹方程为

其中k0为波数,定义为k0=ω/ca;ω=2πf为角频率,f为频率(Hz),zs为源位置,z为声场场点位置,δ(r)狄拉克函数.
利用简正波理论求解等声速浅海信道下点源声场,则信道下点源声场解即信道传输函数G(r,z)可以写为

其中j为复数虚部,ρa为海水密度,为汉克尔函数,ξn为水平行波方向上的特征值;kz为竖直方向的特征值,满足为竖直方向的特征值函数,也称为格林函数,且是一个正交函数族其解由海面、海底边界决定.
海面通常为Dirichlet边界条件,满足边界条件

典型海底边界模型有Neumann边界模型、Rayleigh定律、Sommerfeld模型、Cauchy边界和地声模型[22]等.对于Neumann边界模型、Sommerfeld模型和Rayleigh定律的边界连续方程可表示为:
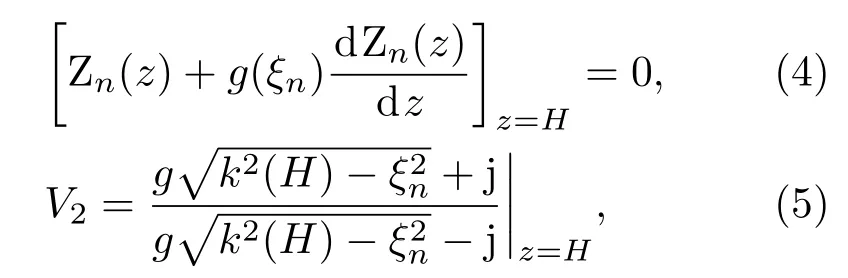
其中g(ξ)由各浅海海底的声学特性决定,定义为为密度,下标a,b分别代表海水与海底;kb为海底波速,定义为为海底声速和吸收系数;V2为海底界面反射系数.
针对较为复杂的Cauchy边界和地声模型,(4)式不再适用,可通过相应的连续方程建立海水-海底接触面上的声反射系数V2.再通过海面、海底的声压反射系数V1(绝对软海面声反射系数V1=−1),V2,便可获取信道下声场传输函数[23].
2.2 信道下波叠加法
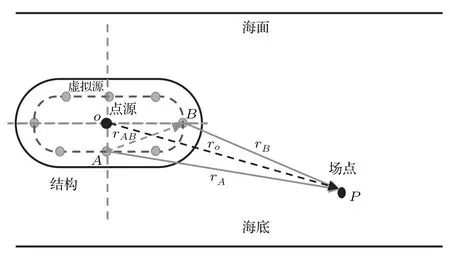
建立如图1所示的浅海信道下结构声辐射预报模型,均质流体密度为ρa,声速为ca;振动体的表面记为S′,U为结构表面法向速度,n为外法向矢量,rs为结构表面一点的位移矢量;Ω为结构内部连续分布的等效声源体,S为与结构共形的虚拟边界面,Q为S上的源强,r0为源强位移矢量,r为Q和P间的距离.
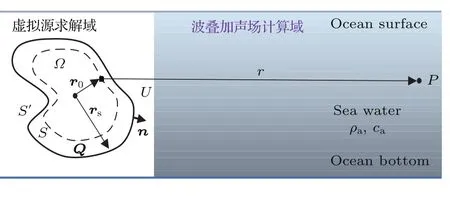
图1 浅海信道下联合波叠加法原理Fig.1.Principle of wave superposition method in shallow water.
波叠加法基本理论与Helmholtz积分公式等效,经离散处理,可由N个简单声源构建复杂振源表面某一点的法向速度[2],
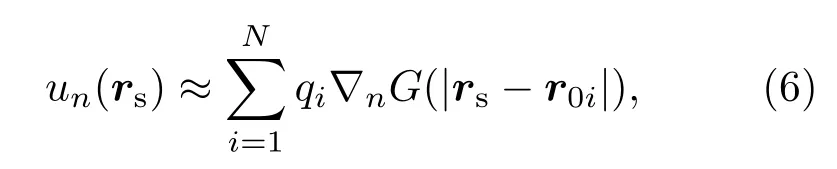
式中qi是虚拟面上第i小段的源强,r0i为各虚拟源的位移矢量,把上式写成矩阵形式:

其中M,N表示矩阵维度,结构表面法向速度矩阵U可通过数值法和实验法获取,D为源强和场点的传递矩阵,定义为一旦配置好等效源,可以通过相应浅海信道环境下的格林函数得到,便可计算虚拟源的源强矩阵Q:
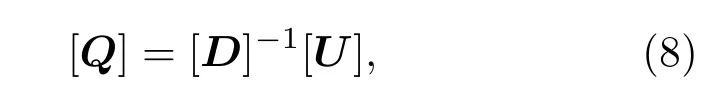
其中[D]−1为[D]的广义逆矩阵,源强的求解涉及非适定性问题,需采用正则化进行大矩阵病态处理[9].
获取结构内部一系列点源源强后,便可求解任意场点的声压:


其中,T为单极矩阵,G为在2.1节已求解的浅海信道传输函数.
2.3 多物理场耦合数值理论
从信道下弹性结构辐射声场波叠加计算式(9)式可知,结构表面速度获取的准确性将决定整个声场计算过程的精度.不同于其他流体环境下结构声振问题,浅海信道下结构辐射声场将受上下界面的重要影响,且由于海底边界类型多、声学参数复杂、地形多变等因素限制,加大了进行浅海信道下结构表面声振信息获取的难度和工作量.因实验法成本高、解析法难以推导,且针对信道下低频声辐射问题,有限元网格量相对较少,所以采用有限元法建立多边界下结构声辐射局域数值模型获取结构表面振动信息是可行的.
建立如图2(a)所示的浅海信道下弹性结构声辐射局域数值计算模型,其中Ωs为结构内部流体域;Ωa为浅海流体介质域;四周Ωp为声学无反射层即完美匹配层(perfectly matched layer,PML)域,其宽度为hPML;内外边界为ΓI,ΓO;Γ为流固耦合边界;Γl,Γh分别为声场与浅海海面与海底交互作用边界.根据对应边界下的连续条件,建立结构与流体,结构与边界耦合方程.
对Helmholtz方程进行权重积分并结合高斯理论,可写出声学有限元方程为

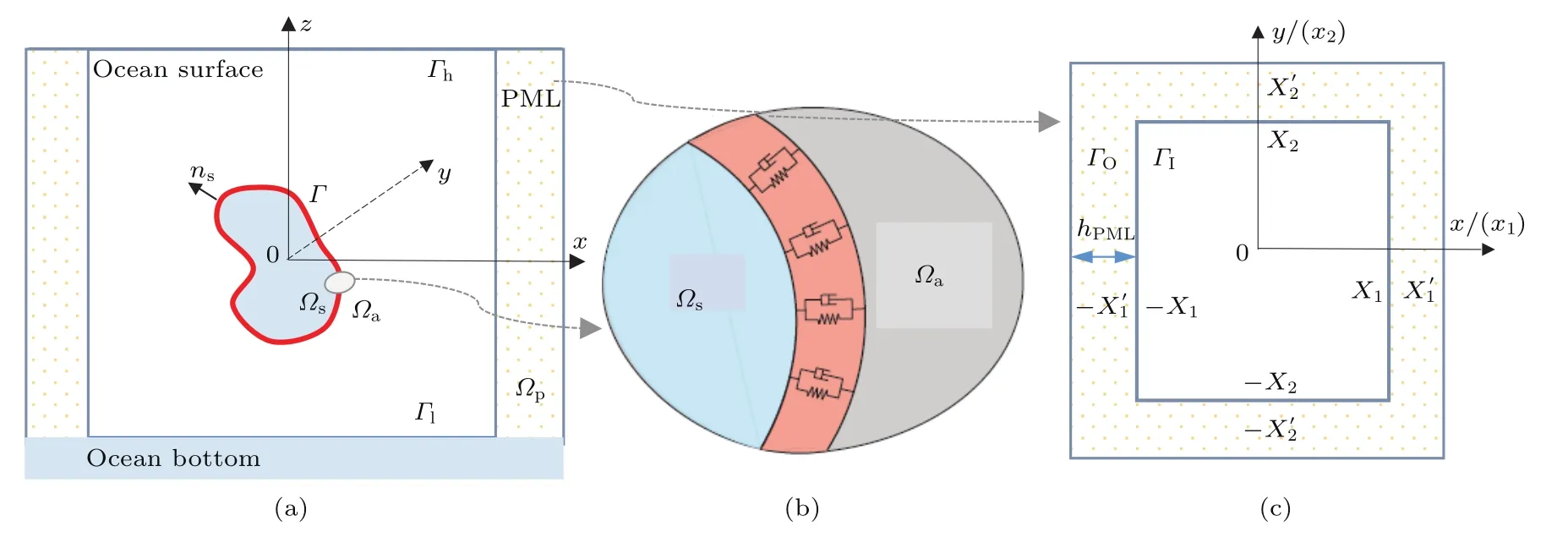
图2 (a)信道下结构多物理场局域数值模型;(b)流固耦合模型;(c)声学完美匹配层Fig.2.(a)Multi-physical field numerical model of structure in the shallow water;(b)fluid-solid coupling model;(c)acoustic perfectly matched layer.
其中{Fi}为声学激励;Mij,Kij和Cij分别为质量矩阵、刚度矩阵和阻尼矩阵,下标a为声学系统矩阵.
类似声学有限元方程推导,对于弹性结构,其有限元振动方程为
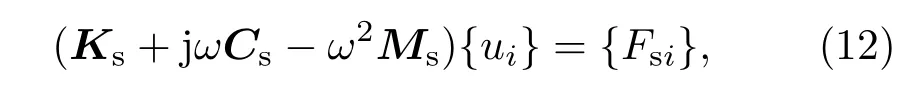
其中Ms,Ks和Cs分别为结构网格上没有受到约束(位移ui)部分的刚度矩阵、质量矩阵和阻尼矩阵;{Fsi}为结构上的激励载荷.
如图2(b)所示,流体域Ωa域与结构的相互作用体现在耦合面Γ上,结构表面法向速度vsn与外部流体介质法向速度van连续

则联立(11),(12)和(13)式,可写出流体域Ωa上结构与流体的耦合方程为

其中Fst,Fat分别为结构、流体介质的耦合载荷;Kc,Mc分别为耦合刚度矩阵、耦合质量矩阵,且各参数详见文献[24].
然后,采用PML技术和边界耦合条件对浅海信道四周边界和上下界面进行声学模拟.建立如图2(c)所示的声学完美匹配层模型,PML通过对控制方程增加吸收系数转换为吸收层的控制方程,为了简化方程描述,令x轴为x1轴、y轴为x2轴,利用分离变量可写出频域下的PML方程:

其中σi为吸收系数;vi,pi为匹配层域的速度和声压幅值.
联立(15)—(17)式,便可求得
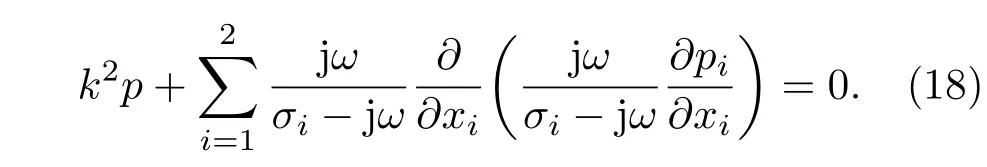
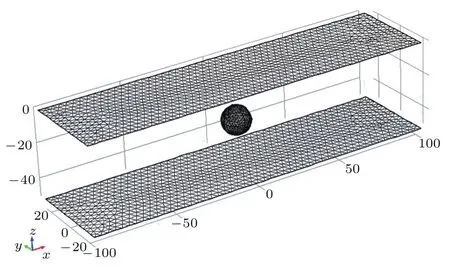
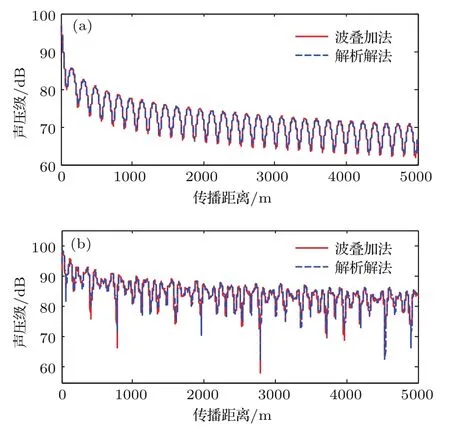
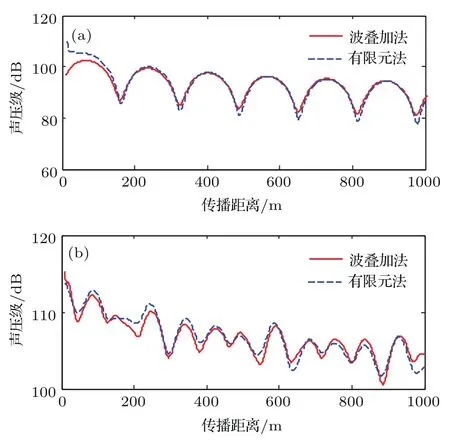
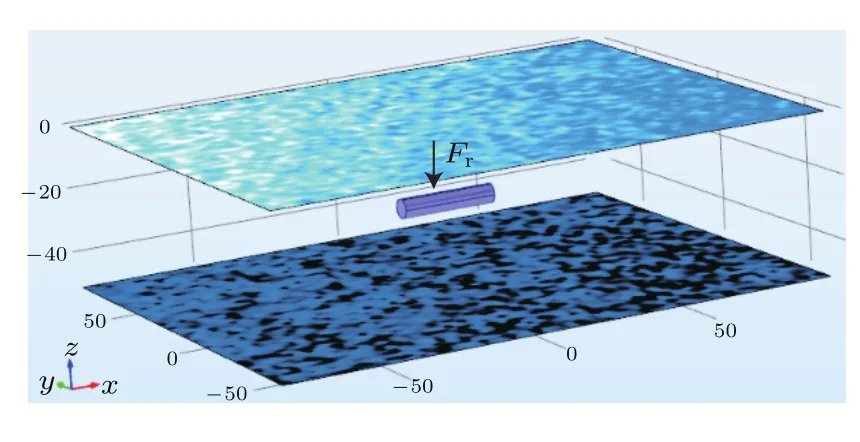
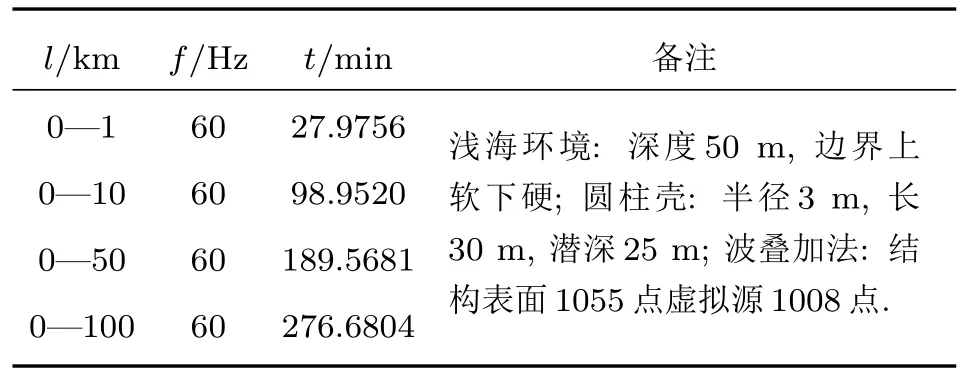
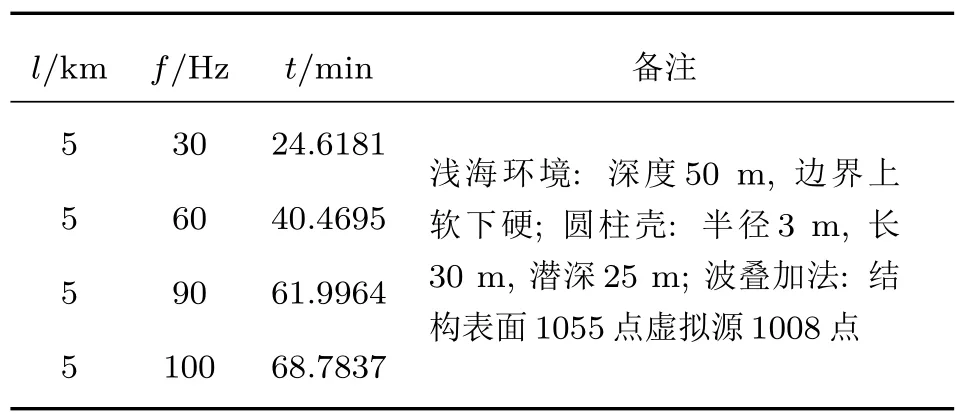
计算流体域包括介质域Ωa和PML域Ωp,两者不同在于PML域有声吸收σi,且σi(x)=σi(−x),当|xi| PML方程与Helmholtz方程可统一写为 PML的作用是在边界上增加几层网格来吸收声学能量,使在该边界上没有反射声以模拟无限远声场边界,其PML网格厚度hPML需大于最大波长λmax的1/15,即hPML>λmax/15. 海面平整边界通常为Dirichlet边界,满足的边界条件为 海底边界模型大致可分为硬海底、液态海底、弹性海底和多孔海底等,在各类海底交互面(z=H)上建立流体介质与海底模型的耦合方程,因连续边界条件涉及的耦合方程较多,这里不再赘述,具体连续方程见文献[25]. 通过数值有限元法建立浅海信道下结构声振问题的流固耦合方程、多边界耦合方程和PML控制方程,并联立各个耦合方程计算获取局部浅海信道流体环境下弹性结构表面准确的振动信息.特别是对于各类复杂的浅海海底,均可通过有限元法建立弹性结构与辐射声、弹性结构与边界反射声的耦合作用,以准确计算在受海面海底边界耦合作用下的结构声振信息.因此,通过有限元法获取振动信息对不同海底(平整海底、粗糙海底、倾斜海底等)的信道环境具有很强的适应性,本文先采用平整的硬海底进行前期研究,以便为后续开展复杂海底(如倾斜的多孔底质海底)的研究奠定基础. 此外,除了采用有限元耦合数值法计算结构表面声振信息以外,还可通过实验方法即在结构表面合理布放振动传感器,实时监测获取弹性结构表面的振动信息,再结合波叠加法便可实时预报弹性结构在浅海信道下的辐射声场,以有效开展浅海信道下潜器辐射声场的实时预报和有效控制. 联合波叠加法计算理论过程为:首先通过2.1节所述的海洋声传播理论求解信道下声场传递函数G,然后按2.3节多物理场耦合数值理论建立局部流域下结构声辐射有限元模型,计算获取多边界影响作用下结构表面准确的振动数据U,并作为波叠加法虚拟源源强Q准确求解的输入条件;最后按2.2节所述的声场波叠加计算法,便可计算流体中任意一点的声场信息P. 建立如图3所示的典型信道环境(海面为Dirichlet边界,海底为Neumann边界)下虚拟脉动球源(并非真实的弹性球壳)有限元数值模型,信道深度h=50 m.小球中心深度为zs=25 m,半径为r0=1 m,在球面各个质点上施加均匀法向振速ua.然后根据表面质点振速,采用波叠加法计算声场信息,并与相同条件下脉动球等效辐射声场解进行对比分析. 图3 信道下虚拟脉动球声辐射有限元网格Fig.3.The finite element mesh of spherical shell in shallow water. 根据虚拟脉动球与点源的等效关系为Q0=脉动球源在信道下的声场等效为信道下的点源声场,按2.1节的简正波理论推导,把浅海海底边界设为Neumann边界,便可求解点源在任意场点的声压表达式 如图4所示,采用波叠加法计算了场点深度为h2=30 m、频率分别为30 Hz和60 Hz下辐射声场的声压级为总声压有效值,pref为在水中取的参考值随距离变化的对比,结果表明本文开发的波叠加法程序与理论解析法计算结果符合得很好. 图4 波叠加法验证 (a)f=30 Hz;(b)f=60 HzFig.4. Verification of wave superposition method:(a)f=30 Hz;(b)f=60 Hz. 建立信道下受激弹性球壳声辐射有限元模型,信道参数与上述验证模型一致;球壳半径为r=1 m,厚度为ht=0.01 m,球壳中心距水面为h1=25 m,材料为钢(密度ρs=7850 kg/m3,杨氏模量Es=2.05×1011Pa,泊松比us=0.28),在顶端施加Fz=1000 N垂直向下的简谐力,结构边界为自由边界.如图5所示,通过有限元计算获取局域环境下结构表面振动数据后,采用波叠加法计算了频率为30 Hz和60 Hz声压级随距离(各场点深度为h2=30 m)的变化曲线,并与有限元计算结果进行对比.可以看出,当达到一定距离后本文所述的波叠加法计算结果与有限元计算结果符合得很好. 简正波法在近场辐射声场计算精度较低,声场计算存在一有效距离,即计算距离大于该距离后,简正波计算精度较高.在理想浅海信道下,该距离定义为[26] 其中H为理想信道深度,λ为声场分析频率对应的波长. 图5 波叠加法与有限元法的对比 (a)f=30 Hz;(b)f=60 HzFig.5. Comparision between wave superposition method and finite element method:(a)f=30 Hz;(b)f=60 Hz. 如图5(a)所示,30 Hz频率下,波叠加法在0—l(l=50 m)距离范围内的计算结果与有限元偏差较大,但当计算距离大于该临近距离l后,两者计算结果符合得很好.如图5(b)所示,60 Hz频率声场计算在远近场声场计算均存在一定的计算精度问题,因为在采用(8)式进行虚拟源源强求解的过程中,由于虚拟源面与结构表面距离较近,而且传递矩阵D中的信道传输函数是通过简正波理论获取的.所以对源强Q求解过程中涉及了近场声场计算精度问题,源强求解精度欠佳.而且在采用(9)式进行声场P求解的过程中也会涉及简正波近场适用性问题,导致在远近场均出现一些偏差,且远场计算精度比近场计算精度要高.虽然可通过波数积分法求解信道传输函数来提高虚拟源求解以及声场计算精度,但因波数积分法求解过程复杂,且采用简正波理论进行波叠加计算推导简单,低频简正波叠加阶数小,计算效率高,计算过程也易于实现,且整体计算精度是满足要求的,所以本文采用简正波法进行传输函数获取以及声场波叠加法计算. 在理论上,虽然可通过增加虚拟源数目来提高波叠加计算精度,但虚拟源点数增加时,简正波近场累积计算误差也在增加.这需要综合考虑虚拟源点数误差和简正波近场计算误差,在满足一定计算精度下,需要合理配置好虚拟源点数.为了进一步完善浅海信道下结构声辐射波叠加法计算理论模型,后续工作将从波数积分法求解浅海信道传输函数和优化虚拟源配置两方面来提高声场波叠加计算精度,以有效地进行复杂浅海信道环境下结构声辐射问题的深入研究. 如图6所示,建立典型浅海信道下(海面Dirichlet边界,海底Neumann边界)圆柱壳声辐射多物理耦合模型,信道环境参数与上述相同.结构为圆柱壳,材料为钢(密度ρs=7850 kg/m3,杨氏模量Es=2.05×1011Pa,泊松比us=0.28),半径为a=3 m,长度为l=30 m,厚度为ht=0.1 m,结构几何中心距水面为h1=25 m,在中间施加径向简谐力Fr=1000 N,结构四周为自由边界,采用PML进行模拟. 图6 信道下结构声辐射模型Fig.6.Acoustic radiation model of structure in shallow water. 利用联合波叠加法计算了圆柱壳结构各频率下声压级随距离变化的曲线,其中场点延伸线沿圆柱壳轴线方向,各场点距离水面均为h2=30 m.为了显示结构在近场声辐射特性与点源产生声场的区别,在进行对比研究之前,需进行相同功率下点源声场的修正,即求解与结构声功率相等条件下的点源声场.设点源功率修正系数ε,使结构辐射声功率Ws与点源声功率Wp相等,即Ws=εWp,得到修正后点源声压级LC 其中LP为修正之前点源在信道下的声压级,∆LP和∆LW为相同声功率下点源声压级和声功率级修正值. 经过相同辐射声功率条件下点源声场修正后,便可进行信道下结构与点源各频率对应的辐射声场特性对比,如图7所示. 图7 近场声辐射对比 (a)f=30 Hz;(b)f=50 Hz;(c)f=100 HzFig.7.Acoustic radiation comparison in near field:(a)f=30 Hz;(b)f=50 Hz;(c)f=100 Hz. 从图7可以看出,当频率为30 Hz时,点源声场特性与结构声辐射特性相差比较小,声场波动规律相似.当f>30 Hz时,结构声辐射曲线与点源声传播曲线无论在变化规律上还是幅度上差别都很大.因为低频时波长相对于结构尺寸比较长,降低了结构尺寸对该频段的声场影响,且低频结构表面振动分布较为均匀;当频率上升到高频时,结构尺寸影响加大.在波叠加法上表示为低频波长相对于结构尺寸较大,结构内部虚拟源因源位置不同而造成相移差别小,近场总声场近似为各虚拟源同相叠加的结果,其变化规律与点源波动趋势基本一致.而随着频率上升,波长减小,在相同距离内波动细节增加,导致各个虚拟源因位置不同而造成相位差异增大,结构辐射的声压级曲线在波动规律与幅值上与点源声场曲线差别较大. 为了充分说明信道下圆柱壳辐射声场与点源声场的区别,计算了信道下结构远程条件下声场(声压级)随距离的变化曲线,并与相应强度的点源传播曲线进行对比,如图8所示. 从图8可以看出,在本文分析的频率范围内,结构声辐射到达一定距离后,30 Hz时结构远距离声压级随距离的变化曲线与点源所对应曲线的波动规律一致,这与之前近场低频声辐射特性和点源相似是一致的,但低频声辐射曲线在波动尖峰具体幅值与点源的声传播曲线是有一定区别的.当频率f>30 Hz时,各频率波动细节因距离不同造成差异增大,虽然远程距离会缩小虚拟源之间的距离差异,在对于大结构远程辐射声场波叠加计算,其置于内部虚拟源的数目众多(本文虚拟源个数为1008个),多个点源的不同相位和幅值的声场叠加增大了场点声场波动细节的差异性;按简正波理论和浅海声传播理论可知,频率增加时远程简正波传播模式增加,与信道上下界面声学作用接触增多,各模式干涉增强.导致结构声辐射和点源声场曲线在远程的波动规律与幅值差异增大,把频率在大于30 Hz下的结构辐射声场等效为点源声场也是不恰当的. 图8 远场声辐射对比 (a)f=30 Hz;(b)f=50 Hz;(c)f=100 HzFig.8. Acoustic radiation comparison in far field:(a)f=30 Hz;(b)f=50 Hz;(c)f=100 Hz. 图9 计算了水平距离圆柱壳中心500 m处圆柱壳与点源在在深度方向上的归一化辐射声压,由于信道上下边界的存在,各频率在深度方向的声场分布出现了类似驻波的分布形式,因为信道上边界为Dirichlet软边界,下边界为Neumann边界,这种深度方向声场分布规律与一端自由一端固定边界的弦振动模式类似.在水深为50 m、频率为30 Hz下,在深度方向上刚好包含一个完整的驻波形式,而且结构在深度方向的辐射声场与点源在深度方向的声场波动规律一致,在该距离和频率条件下,圆柱壳在深度方向的辐射声场可等效为点源声场;当频率高于30 Hz后,两者在深度方向的波动规律以及归一化幅值差别变大,因为波叠加法计算时内部包含多个不同点源,各个点源经过信道上下界面反射作用后进行干涉叠加,所以圆柱壳在深度上辐射声场不能可用一个点源的声场代替. 图9 深度上声场对比 (a)f=30 Hz;(b)f=50 Hz;(c)f=100 HzFig.9.Contrast of sound field in the depth:(a)f=30 Hz;(b)f=50 Hz;(c)f=100 Hz. 如图10所示,场点选择在距离结构中心为l且深度为h的圆周上,极角0◦和90◦处分别对应圆柱壳结构端面和侧面,水平上相连两个场点之间的夹角θ=1/200 rad.从图11可看出,当圆柱壳信道环境下声辐射频率在30 Hz时,无论在传播距离上还是深度方向上的声场空间分布图都趋于圆形,在该频率下是可以等效为无指向性的点源声场;当频率高于30 Hz时,其三维空间分布均随深度和距离方向的改变而改变,圆柱壳在信道下的空间声场分布的变化规律与上述在距离和深度方向上与点源声场对比得出的规律是一致的. 为了分析柱等弹性结构辐射声场特性与点源声场差异性的物理机理,建立结构声场波叠加计算和点源声场模型,如图12所示,并结合等效源理论、结构振动和海洋声传播等方面的理论进行研究分析. 图10 水平方向场点选择示意图Fig.10.Diagram of horizontal field selection. 根据理想信道下声场传递函数(22)式和源强求解(8)式可求解圆柱壳内部各个虚拟源强度.首先,由于各个虚拟源空间位置不同,所以任意虚拟源A和B的源强Q的幅值和相位也不相同.其次,弹性结构表面振速考虑了信道上下边界的影响,所以各虚拟源源强求解也考虑了海面海底的反射声作用,信道下弹性结构声辐射考虑了结构与流体、边界的相互作用,这不同于单个点源产生声场的特性.最后,在结构近场虚拟源A和B到场点P的距离rA和rB相差较大.虽然,低频条件下,结构表面振速分布较为均匀,但近场各点到场点的距离相差较大,虚拟源A和B对场点P作用声场的幅值、相位差别进一步增大.空间分布的各虚拟源在近场场点不同幅值的声场叠加,导致弹性圆柱壳等效辐射声场的波动不同于单个点源产生的声场,不可进行结构辐射声场的点源等效. 在远场条件下,场点P距离任意虚拟源A和B的距离rA和rB远大于相对于虚拟源之间的距离rAB,可认为rA=rB.所以各虚拟源在场点P的声场作用只与虚拟源源强幅值和相位相关.且频率较低如30 Hz时,结构表面振速分布较为均匀,所以通过表面振速求解的各虚拟源源强之间差距较小,且任意虚拟源A与点源距场点P的距离基本相等即rA=ro,所以弹性结构在远场辐射声场与点源产生的声场分布规律基本一致,但随着频率的增加,受界面影响下的结构表面振速分布差异增大,声场指向性分布更加复杂.且波长较短波动细节增加,声场简正波的阶数增加,通过结构表面振速反演虚拟源源强的差距增加;而且随着频率的增加,声与上下边界作用的次数增加,场点声场的干涉叠加作用也变得更加复杂,从而导致通过各虚拟源产生声场叠加得到的结构等效辐射声场与单个点源差别增大. 图11 声场在不同距离空间分布 (a)f=30 Hz,l=20 m;(b)f=30 Hz,l=50 m;(c)f=30 Hz,l=100 m;(d)f=50 Hz,l=20 m;(e)f=50 Hz,l=50 m;(f)f=50 Hz,l=100 m;(g)f=100 Hz,l=20 m;(h)f=100 Hz,l=50 m;(i)f=100 Hz,l=100 mFig.11.Spatial distribution at dif f erent distance:(a)f=30 Hz,l=20 m;(b)f=30 Hz,l=50 m;(c)f=30 Hz,l=100 m;(d)f=50 Hz,l=20 m;(e)f=50 Hz,l=50 m;(f)f=50 Hz,l=100 m;(g)f=100 Hz,l=20 m;(h)f=100 Hz,l=50 m;(i)f=100 Hz,l=100 m. 图12 结构与点源辐射声场示意图Fig.12. The schematics of acoustic structure and point source radiation. 为了显示该方法在计算速度方面的优势,进行了三维条件下大型结构远距离声场计算时间分析,分别对不同距离和不同频率下的程序计算时间进行测试,测试运行结果如表1和表2所示. 从表1和表2可看出,该方法可快速进行信道环境下大型结构辐射声场计算,相比于相同硬件条件下当用有限元数值软件计算上述声辐射问题,当频率取100 Hz计算距离为500 m时,网格计算量将达到千万量级而难以计算,但通过信道下波叠加算法便可在数小时之内完成声场快速计算. 表1 不同距离范围声场计算时间Table 1.Calculation time of dif f erent distance ranges. 表2 不同频率声场计算时间Table 2.Calculation time of dif f erent frequencies. 浅海信道下声场特性与其他流体环境下声场特性不同的主要原因在于上下界面对声场的影响,主要表现为界面反射声不仅作为结构二次声激励,而且还会对场点声场具有干涉叠加作用.为了考虑上下界面对声场影响,本文选择竖直方向上的空间声场进行分析,场点选择如图13所示,圆柱壳中心离水面h1=25 m,场点选择在离结构中心25 m的圆周上,圆周所在平面垂直圆柱壳轴线,极角90◦和270◦处分别对应海面和海底. 对比三种流体环境下竖直圆周上的声场空间分布可看出,边界的存在使在靠近边界处的空间声场分布出现较大波动,信道下结构辐射声场由于同时受信道上下界面的影响,在竖直方向上为驻波场,导致在圆周上均出现明显的旁瓣,且不同频率下上下界面对整个圆柱壳辐射声场分布影响作用不同,如当频率为200 Hz时,在上半圆周上的声场分布已经受到了下界面的严重影响,而不会出现上(下)边界只单独影响上(下)半圆周的声场分布规律;但频率为30,50和100 Hz时,信道环境和半空间环境下辐射声场在上半圆周的声场分布趋于一致,半空间和自由场环境下辐射声场在下半圆周的声场分布规律相同.同样,相对于较高频率,30 Hz和50 Hz频率下辐射声压空间分布波动较小,在竖直方向上的空间分布曲线类似为圆形,随着频率的增加,辐射声压在空间分布的旁瓣数量增加.而且由于信道下场点总声场由不同成分的界面反射式与直达声干涉叠加构成,信道下的叠加声压波动峰值大于自由场以及半空间下的辐射声压幅值(见图14). 图13 竖直方向场点选择示意图Fig.13.The diagram of vertical field selection. 图14 不同流体环境下声压级对比 (a)f=30 Hz;(b)f=50 Hz;(c)f=100 Hz;(d)f=200 HzFig.14.Comparison of radiation sound pressure levels in dif f erent fluid environments:(a)f=30 Hz;(b)f=50 Hz;(c)f=100 Hz;(d)f=200 Hz. 目前,在舰船辐射噪声测量的实际工程应用中,常用较为简单、易实现的垂直或水平线列阵测量方法.不同于自由场和半空间环境下的辐射声场测量,浅海信道下各阵元测量的声场信息包含了界面反射声的多次叠加作用,而且上下界面各自影响作用与边界类型、结构潜深和分析频率等因素密切相关,导致信道下结构辐射声场测量比自由场以及半空间环境下的辐射声场测量更加复杂.下面通过数值模拟垂直阵测量浅海信道下结构辐射声场来说明该问题. 如图15(a)所示,建立浅海信道下结构声辐射垂直线列阵测量模型,竖直方向上两阵元之间的距离为2.5 m,阵元个数为20,同一水平面上相邻两阵元到中心连线夹角为3◦.用垂直线列阵围绕结构一周便可测量结构在横扫面S上的辐射声功率;信道环境参数与上述相同,圆柱壳结构中心距离水面25 m.保持结构激励条件和环境参数不变,采用波叠加法分别计算了各个模拟测点的声场信息,并与不同环境以及不同深度下的测量结果进行对比. 图15 垂直线列阵辐射声场测量结果 (a)垂直线列阵测量示意图;(b)单个水听器测量结果;(c)不同环境下声功率对比;(d)不同潜深下声功率对比Fig.15.The radiation sound field measurement results used vertical line array:(a)The vertical line array;(b)the measurement of single hydrophone;(c)the comparison of acoustic radiation power;(d)the acoustic radiation power in the dif f erent diving depths. 图15 (b)为垂直线列阵中各阵元水平距离结构中心40 m处即阵元坐标为(0,40,−25),在不同流体环境下测量得到的辐射声压值(声压级)随频率变化的曲线,且三种流体环境边界条件下的结构边界条件、距水面距离和激励条件等因素保持不变.可以看出,由于边界反射声的影响,任意场点的声场是由直达声与界面反射声干涉叠加作用的结果,辐射声场的声压幅值较大.所以在信道下由阵元测量获得均方声压,并变换得到的声压级明显比自由场和半空间下的声压级要大. 如图15(c)所示,利用水平距离结构中心40 m的垂直线列阵围绕圆柱壳一周后,测量得到其在不同流体环境边界下的辐射声功率为辐射声在包络面S上的声能量Ir积分即参考级随频率的变化曲线,因为信道上下边界限制了圆柱壳辐射声能量向外传播,信道内集中了大部分声能量,所以辐射声功率整体高于半空间以及自由场条件下的辐射声功率.而且在信道内由于结构距离上下边界的距离不同,上下边界对圆柱壳辐射声能量的“束缚”作用也不同. 如图15(d)所示,分别计算了圆柱壳中心处于不同信道深度下的辐射声功率曲线.当结构中心处于不同深度时,结构距浅海上下边界的距离不同,上下边界反射声对结构振动和辐射声场的影响作用也不一样,导致用垂直线列阵测量出来的辐射声功率差异很大.而且对于低频辐射噪声,通过增加下潜深度可明显降低其辐射声功率大小,这为在浅海环境下进行潜器辐射声场测量以及声隐身提供了一些参考. 本文通过联合声场简正波理论、多物理场耦合有限元法和波叠加法建立了浅海信道下弹性结构辐射声场计算的理论方法.并从数值法和解析解法两方面验证了该方法计算结果的准确性和可靠性,同时经过时间测试说明了该方法计算的效率性后,从辐射源、流体环境影响和辐射声场测量的角度研究分析了浅海信道下圆柱壳声辐射特性,主要得出以下结论. 1)浅海信道下辐射源等效:通过圆柱壳与相同功率条件下点源在距离、深度方向和空间声场分布特性进行对比得出,在低频如本文所分析的f=30 Hz下,结构声场特性与点源相差比较小,在远场是可以把结构声场特性用点源声场特性来等效替代的,当f>30 Hz时圆柱壳声辐射曲线与点源声传播曲线在变化规律和幅度以及空间分布上差别较大,用点源替代其声场特性是不恰当的. 2)流体环境边界对圆柱壳声辐射特性的影响:信道下低频辐射声场空间分布规律与自由场以及半空间基本相同,在整个圆周上的分布无明显指向性,分布形状类似圆形,但随着频率升高,声场指向性分布逐渐明显.信道下圆柱壳辐射声场与自由场以及半空间环境下的辐射声场空间分布特性差异比较大,主要表现为信道下辐射声场分布会出现明显的指向性分布,而且上下边界会耦合作用于场点总声场的空间分布规律. 3)辐射声功率测量:在利用垂直线列阵进行信道下圆柱壳辐射声功率测量时,其辐射声场的测量结果与自由场以及半空间的测量结果差异较大,下潜深度对测量结果的影响尤为明显;在低频,增加下潜深度可以明显降低圆柱壳的辐射声功率值. 上述结论为以后更好地开展信道环境下弹性结构辐射声场预报、声学测量和减振降噪等领域的研究提供了一些新的参考,同时也说明了该方法能有效地解决目前在进行浅海信道下大型弹性结构远程声辐射预报过程中所涉及的计算量大、耦合物理场多和信道环境复杂等问题,为开展复杂浅海信道环境下的任意弹性结构声辐射的研究提供了一种新的解决途径. 此外,本文作为前期理论建模和数值分析的研究总结,其理论研究层次上有待进一步深入,今后将考虑从浅海信道下结构声辐射实验进行该方面理论体系的完善和提高. 感谢课题组王曼、张超、刘永伟等老师给予论文的帮助以及与孙启航、刘佳琪、丁丹丹等同学的讨论. [1]Zhang Y G 2014The Ef f ect and Application of Acoustic Photoelectric Waveguide(Beijing:Publishing House of Electronics Industry)pp117–125(in Chinese)[张永刚2014海洋声光电波导效应及应用(北京:电子工业出版社)第117—125页] [2]Koopmann G H,Song L,Fahnline J B 1989J.Acoust Soc.Am.86 2433 [3]Miller R D,Moyer Jr E T M,Huang H,Überall H 1991J.Acoust Soc.Am.89 2185 [4]Fahnline J B,Koopmann G H 1991J.Acoust Soc.Am.90 2808 [5]Jeans R,Mathews I C 1992J.Acoust Soc.Am.92 1156 [6]Yu F,Chen X Z,Li W B,Chen J 2004Acta Phys.Sin.53 2607(in Chinese)[于飞,陈心昭,李卫兵,陈剑2004物理学报53 2607] [7]Li W B,Chen J,Bi C X,Chen X Z 2006Acta Phys.Sin.55 1264(in Chinese)[李卫兵,陈剑,毕传兴,陈心昭2006物理学报55 1264] [8]Xiong J S,Wu C J,Xu Z Y,Zeng G W 2011Chin.J.Ship Res.6 41(in Chinese)[熊济时,吴崇健,徐志云,曾革委2011中国舰船研究6 41] [9]Li J Q,Chen J,Yang C,Jia W Q 2008Acta Phys.Sin.57 4258(in Chinese)[李加庆,陈进,杨超,贾文强2008物理学报57 4258] [10]Chen H Y,Shang D J,Li Q,Liu Y W 2013Acta Acoust38 137(in Chinese)[陈鸿洋,商德江,李琪,刘永伟 2013声学学报38 137] [11]Zhan G Q,Mao R F 2016J.Nav.Univ.Eng.28 4(in Chinese)[詹国强,毛荣富2016海军工程大学学报28 4] [12]Gao Y,Cheng H,Chen J 2008Trans.Chin.Soc.Agric.Mach.39 173(in Chinese)[高煜,程昊,陈剑 2008农业机械学报39 173] [13]Wang Y M 2013Ph.D.Dissertation(Harbin:Harbin Engineering University)(in Chinese)[王玉明 2013博士学位论文(哈尔滨:哈尔滨工程大学)] [14]Pan H J,Li J Q,Chen J,Zhang G C,Liu X F 2006China Mech.Eng.17 733(in Chinese)[潘汉军,李加庆,陈进,张桂才,刘先锋2006中国机械工程17 733] [15]Bai Z G,Wu W W,Zuo C K,Zhang F,Xiong C X 2014J.Shi.Mech.1–2 178(in Chinese)[白振国,吴文伟,左成魁,张峰,熊晨熙2014船舶力学 1—2 178] [16]Zou Y J,Zhao D Y 2004J.Vib.Eng.17 269(in Chinese)[邹元杰,赵德有2004振动工程学报17 269] [17]Wang P,Li T Y,Zhu X 2017J.Ocean Eng.142 280 [18]Zhang R H,He Y,Liu H,Akulichev V A 1995J.Sound Vib.184 439 [19]Qin J X,Boris K,Peng Z H,Li Z L,Zhang R H,Luo W Y 2016Acta Phys.Sin.65 034301(in Chinese)[秦继兴,Boris K,彭朝晖,李整林,张仁和,骆文于2016物理学报65 034301] [20]Luo W Y,Yu X L,Yang X F,Zhang Z Z,Zhang R H 2016Chin.Phys.B25 124309 [21]Porter M B,Bucker H P 1987J.Acoust Soc.Am.82 1349 [22]Etter P C(translated by Cai Z M)2005Underwater Acoustics Modeling and Simulation(3rd Ed.)(Beijing:Publishing House of Electronics Industry)pp83–88(in Chinese)[埃特 著 (蔡志明 译)2005水声建模与仿真(第3版)(北京:电子工业出版社)第83—88页] [23]Brekhovskikh L M,Lysanov Y P 2004Fundamentals of Ocean Acoustics(3th Ed.)(New York:Acoustics Springer)pp72–114 [24]Marburg S,Nolte B 2008Computational Acoustics of Noise Propagation in Fluids-Finite and Boundary Element Methods(New York:Acoustics Springer)pp166-178 [25]Jackson D R,Richardson M D(translated by Liu B H,Kan G M,Li G B)2014High-Frequency Seafloor Acoustics(Beijing:Ocean Press)pp240–260(in Chinese)[杰克森,理查德森著(刘保华,阚光明,李官保 译)2014高频海底声学(北京:海洋出版社)第240—260页] [26]Weston D E 1963Radio Ele.Eng.26 329
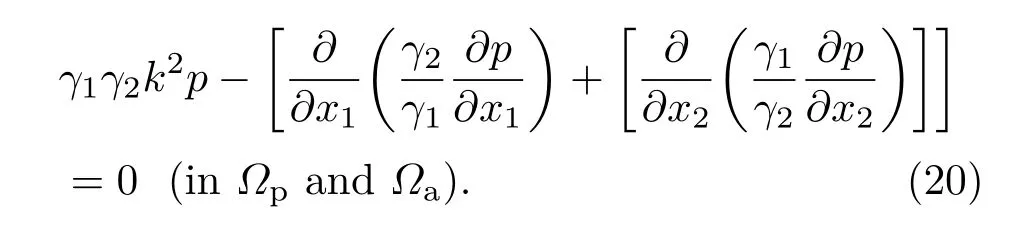

3 信道下圆柱壳声辐射特性分析
3.1 信道下波叠加法验证


3.2 信道下声辐射源分析

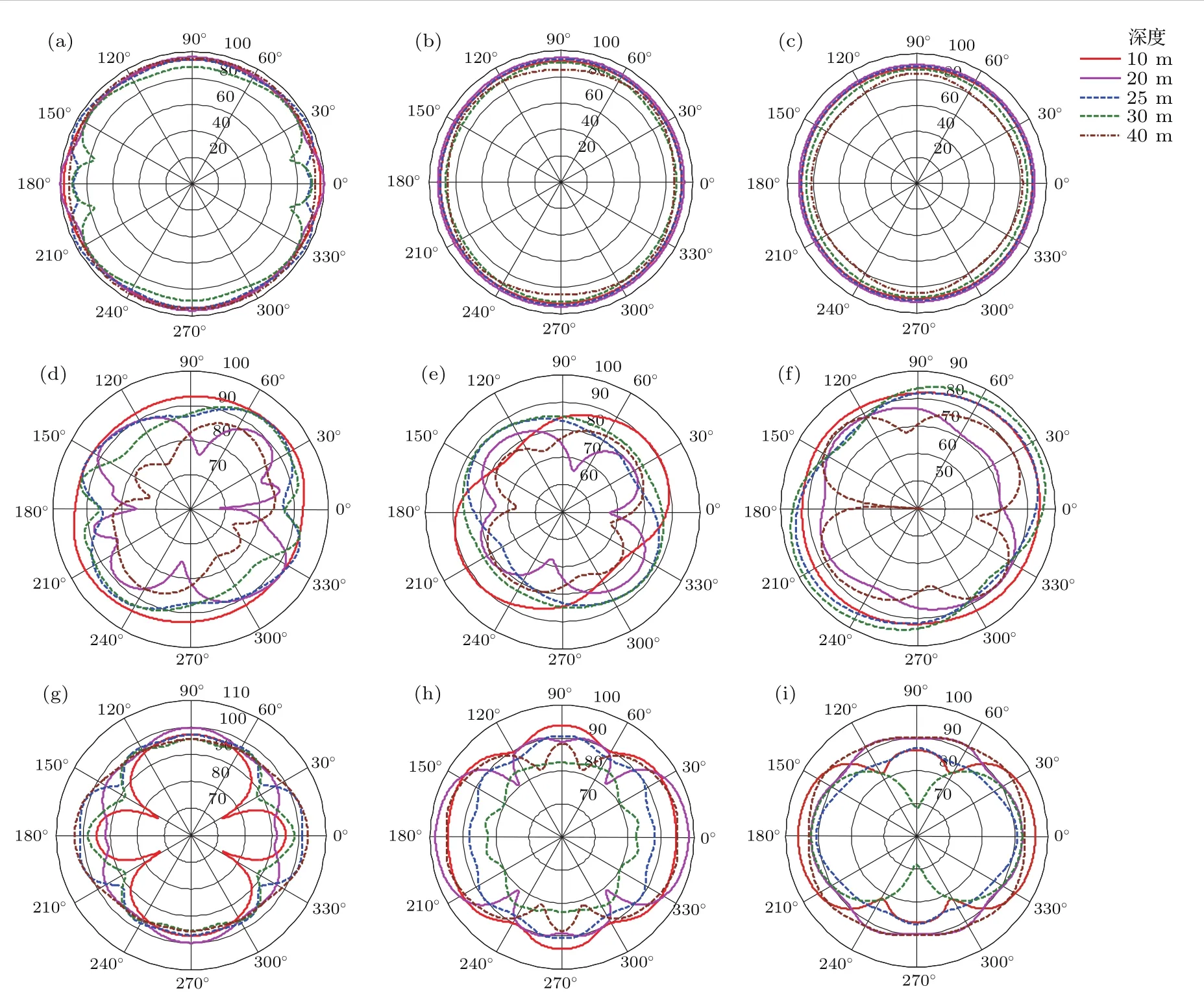
3.3 信道下声辐射分布

3.4 信道下辐射声场测量分析

4 结 论

