铷原子气体自旋噪声谱的测量与改进∗

尚雅轩马健史平钱轩李伟姬扬

1)(中国科学院半导体研究所,半导体超晶格国家重点实验室,北京 100083)

2)(中国科学院大学材料科学与光电技术学院,北京 100049)

3)(中国科学院大学物理科学学院,北京 100049)

4)(挪威科技大学海事操作与土木工程系,奥勒松6025,挪威)

(2018年1月15日收到;2018年2月7日收到修改稿)

1 引 言

自旋噪声谱(spin noise spectroscopy,SNS)技术是一种新型的探测手段,用于研究系统自旋处于平衡态时的性质,无需向系统注入自旋,仅用一束功率较低的探测光即可探测到系统的稳态自旋涨落.这种自旋电子学的实验方法能够得出自旋动力学的很多重要信息[1,2].

早在1981年,Aleksandrov和Zapassky[3]就预言了噪声测量可在磁学探测中实现,Crooker等[4]在2004年首次成功测量了碱金属铷原子气的自旋噪声谱.随后Oestreich等[5,6]将这种方法应用到半导体材料中,测量了n型GaAs体材料中导带电子的自旋噪声谱,并于2007年利用快速傅里叶变换(FFT)频谱分析仪测量自旋噪声,比传统的扫描频谱仪测量效率更高.随着自旋噪声谱方法的改进,其应用更加广泛.2010年,Crooker等[7]报道了半导体量子点体系中的自旋噪声谱,并首次将高速数据采集与现场可编程门阵列(field-programmable gate array,FPGA)结合,在自旋噪声谱的测量中进行了应用.Oestreich等[8]从量化误差的角度出发,对实验中所能达到的精度极限信噪比(signalnoise ratio,SNR)做了评估,最大值为0.01N,其中N为累加次数.

自旋噪声测量的是自旋信号在其均值附近的随机涨落.给样品施加横向磁场,使自旋以拉莫尔频率进动.涨落自旋拉莫尔进动的幅度非常小,高效率探测的技术核心是:对时域信号做FFT,由于系统中噪声都是非周期性的,只有自旋的进动信号会在特定频率处产生自旋噪声峰,峰半高宽对应于自旋弛豫时间;对微弱信号(微伏量级)进行高速采集和快速处理,通过减去背景噪声谱来消除固有噪声,利用多次累加求平均来削减白噪声.基于FPGA芯片,可以将高速数据采集与实时傅里叶变换相结合,从而缩短测量时间、提高测量效率[9,10].本课题组以前的工作[11]对测量自旋噪声谱的几种方法进行了分析和研究,基于FPGA的实时傅里叶变换采集卡(data-aquisition card with real time fast Fourier transforms,FFTsDAC)比传统的频谱仪和数据采集卡的数据利用率和测量效率更高,具有更好的信噪比.

本文以铷原子系统自旋噪声的测量为例,具体介绍微伏量级微弱信号的提取以及系统中固有噪声的去除.实验中,改变了探测光光强,对自旋噪声测量系统的背景噪声(SBN)以及自旋噪声信号(SSN)随探测光光强的变化关系进行了详细讨论,背景噪声SBN与探测光光强成正比,自旋噪声信号SSN与探测光光强的平方成正比,同时证实了自旋噪声确实来自于系统中自旋的随机涨落.比较了两种FFTsDAC(分别是8 bit采样的FFTsDAC1和12 bit采样的FFTsDAC2)的测量性能,分析了影响实验信噪比的因素.FFTsDAC2测量效率和采样深度比FFTsDAC1有所提高,从而具有更高的信噪比.此外,FFTsDAC2单次采样时间更长,因而频率分辨率更高,其测得的谱线半高宽更窄、更准确.本文还对频率分辨率不同的采样设备的自旋噪声测量过程进行了数值模拟,与实验结果一致.

2 测量铷原子自旋噪声谱的实验系统

自旋噪声谱的测量原理是将热平衡系统的自旋的随机涨落映射到线偏振探测光的偏振变化上(法拉第旋转),其实验系统由光电转换模块和数据处理模块两部分组成(图1(a)).随时间起伏的法拉第旋转由光电转换模块转换为电压值,被探测器实时记录.具体过程如下:采用Ti宝石激光器产生780 nm左右的激光,经过起偏器后的线偏振光汇聚到长度为60 mm且温度可控的原子气室中.本文采用了两种具有不同浓度缓冲气体的铷原子气样品(包含两种同位素:天然丰度约72.15%的85Rb和27.85%的87Rb):样品1为充有250 Torr(1 Torr≈133.322 Pa)的N2;样品2为充有100 mTorr的N2.线偏振探测光通过施加横向磁场的样品后,产生法拉第旋转,再经过半波片和沃拉斯顿棱镜后进入差分探测器,记录探测光偏振的变化,得到的差分信号即为法拉第信号.由光电转换模块得到的电信号传送至FFTsDAC,在板卡内通过FPGA实现频谱转换和频谱累加.光路中的声光调制器(acousto-optic modulator,AOM)是用于验证自旋涨落是随机的,见4.2节.

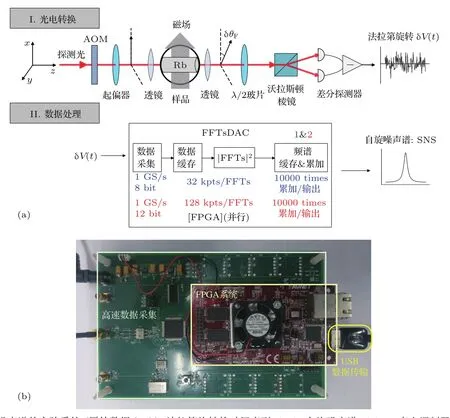
图1 (a)自旋噪声谱的实验系统(原始数据δV(t),法拉第旋转的时间序列;SNS,自旋噪声谱;AOM,声光调制器);(b)自主设计并制作的基于FPGA的FFTsDAC面板Fig.1.(a)Schematics of the spin noise spectroscopy measurement system(δV(t),time-dependent Faraday rotation signal,i.e.,raw data;SNS,spin noise spectrum;AOM,acousto-optic modulator);(b)a self-made FPGA based DAC with FFTs(FFTsDAC).

采集卡每次采集数据后(两种采集卡的每次采样数分别为32 kpts和128 kpts),FPGA程序将数据进行FFT并取模平方得到功率谱,实现一次采集;随后重复该过程,并将存在采集卡缓冲区的功率谱进行不断累加,每进行10000次累加后,将累加结果传输至计算机,从而得到自旋噪声谱.为了消除系统中存在的一些固有噪声,将零磁场下测得的噪声谱作为背景谱线SBN,把目标磁场下测得的谱线ST减去背景谱线,从而得到最终的自旋噪声谱SSN.FFTsDAC的核心构件——FPGA面板(图1(b))集成了高速数据采集、实时傅里叶变换、数据缓存及谱线累加平均等多项功能,可以实时测量、并行处理、互不干扰、独立完成,高效地利用了时域的采样数据.这种测量方法得到的频谱受限于采样定理[12],频谱带宽受限于采样率,wspan=νs/2,其中wspan为频谱带宽,νs为采样率;分辨率带宽则受限于单次采样时间,wRBW∝1/T,其中wRBW为分辨率带宽,T为单次采样时间.

3 测量过程中固有噪声的去除

在热平衡状态下,系统的自旋随机涨落引起的自旋极化信号非常微弱,所测的自旋噪声信号幅度大约只有微伏量级[5].实验系统中固有噪声(包括激光散粒噪声,电压幅度约为30µV;以及探测器电子噪声,电压幅度约为200µV等[13])对自旋噪声的测量影响很大,必须尽可能地去除系统中固有噪声.因此,先在零磁场下测量得到背景噪声谱SBN,将目标磁场下测得的包含信号的谱线ST减去背景谱线SBN,从而得到样品的自旋噪声谱信号SSN.

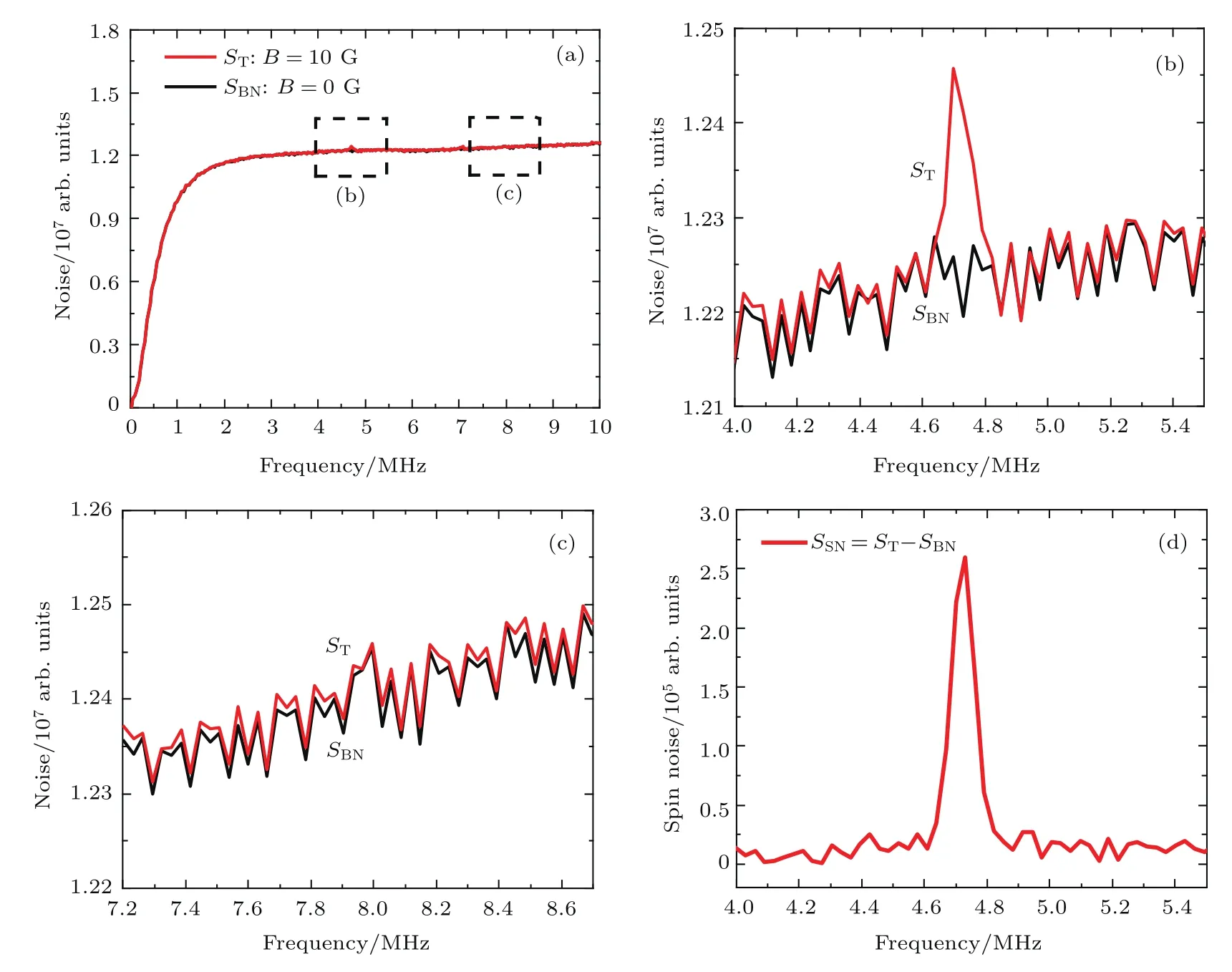
图2 固有噪声去除示意图 (a)在外加横向磁场B=10 G(1 G=10−4T)时测量得到的铷原子气样品的自旋噪声信号谱线ST和外加磁场B=0 G时测量得到的背景噪声谱线SBN;(b)在拉莫尔进动频率附近,信号谱线与背景谱线存在一定差异;(c)远离拉莫尔进动频率时,信号谱线与背景谱线几乎完全重合,其幅度均约为107;(d)将自旋噪声信号谱线减去背景谱线,得到铷原子气的自旋噪声谱SSN,信号幅度约为105Fig.2.A schematic diagram shows how to remove intrinsic noise:(a)Spin noise spectra of rubidium atomic gas(B=10 G,1 G=10−4T)and background noise(B=0 G);(b)around the Lamor frequency,spin noise spectroscopy and background noise are dif f erent;(c)being far away from the Lamor frequency,spin noise spectroscopy and background noise are almost the same(about 107);(d)spin noise spectra of rubidium atomic gas(about 105)after eliminating the background noise.

基于自旋噪声谱测量系统,利用500µW的探测光测量样品1(充有250 Torr N2作为缓冲气体的铷原子气)的自旋噪声谱如图2(d)所示.图2(a)为在目标磁场B=10 G时测量得到的包含自旋噪声信号的谱线ST和在无外加磁场的情况下测得的背景噪声谱SBN.为更好地比较二者的差异,将拉莫尔频率ν=gµBB/h(g为朗德因子,µB是玻尔磁子,B为外加横向磁场,h为普朗克常数)[14]附近(4.0—5.5 MHz)和远离拉莫尔频率(7.2—8.7 MHz)的谱线放大,分别如图2(b)和图2(c)所示.前者信号谱线与背景谱线在4.76 MHz(拉莫尔频率)附近存在一定差异,而后者的两条谱线几乎完全重合.减除背景噪声谱之前,噪声谱幅度约为107.图2(d)为信号谱线减去背景谱线得到的铷原子气自旋噪声信号,幅度约为105.通过减去背景谱线,去除了固有噪声的影响,从而得到自旋噪声信号.

4 结果与讨论

4.1 自旋噪声谱随探测光光强变化

碱金属铷原子是类氢原子,最外层惟一的s轨道价电子决定了其光学性质.用D1线和D2线来分别表示价电子在52S1/2↔52P1/2和52S1/2↔52P3/2之间的跃迁.本实验采用的探测光波长位于780 nm处,测量的铷原子自旋噪声谱主要来自于D2线[15,16],如图3(a)所示[17].测量时将探测光频率调至距离铷原子D2(52S1/2↔52P3/2,780 nm)的中心频率约5 GHz,所加外磁场B=10 G,温度T=318 K,所得自旋噪声谱存在两个明显的峰,分别对应于85Rb和87Rb自旋噪声峰,其频率位置分别为4.73 MHz和7.04 MHz,对应于横向磁场B=10 G时的铷原子拉莫尔频率ν=gµBB/h.根据上式的峰位计算可得铷原子两种同位素85Rb和87Rb的有效g因子分别为gF≈0.338和gF≈0.503,与理论值gF=1/3和gF=1/2相符[18,19].

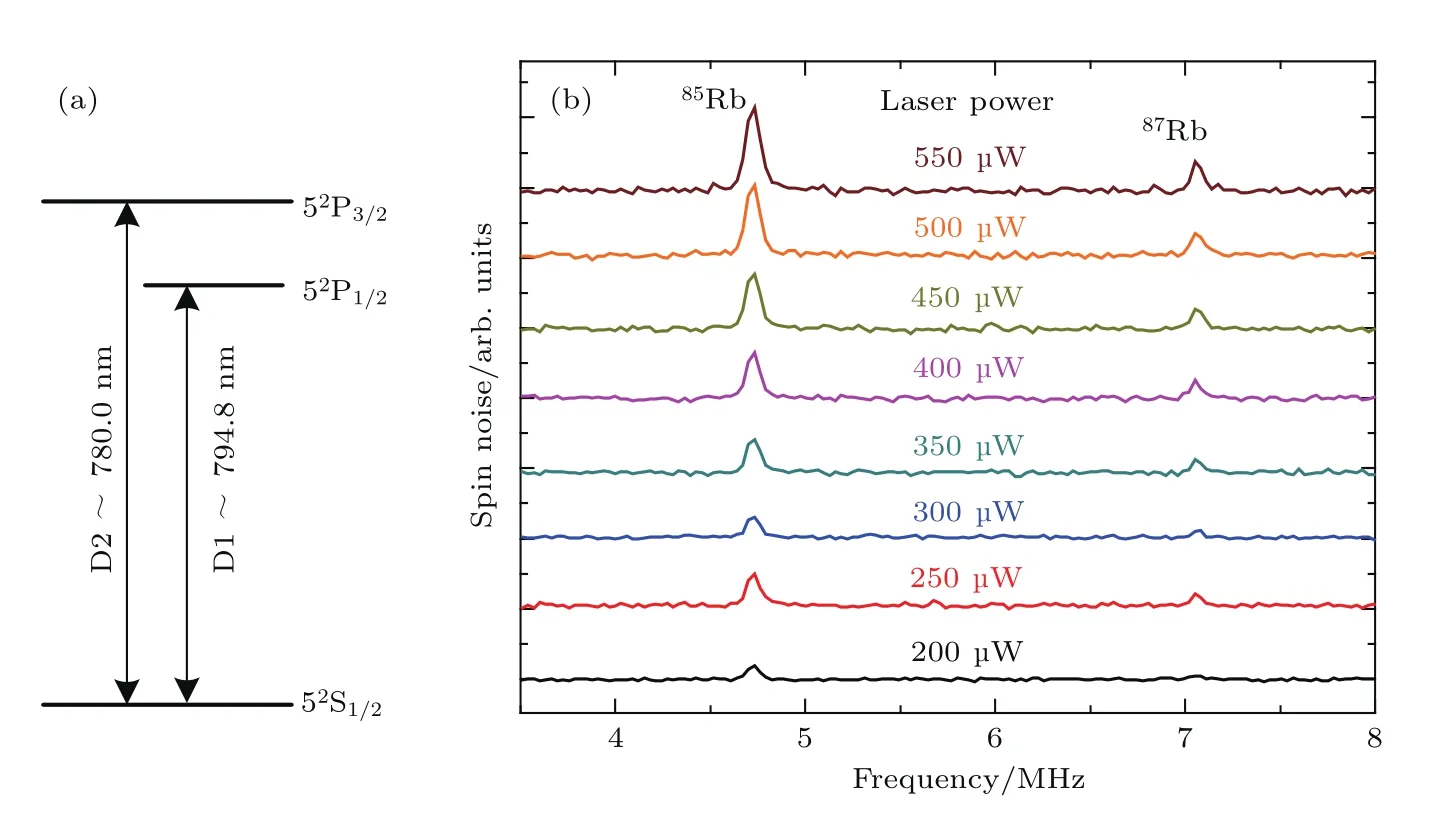
图3 (a)铷原子D1线和D2线能级结构;(b)充有250 Torr N2缓冲气体的铷原子气,自旋噪声谱随探测光功率的变化Fig.3.(a)D1-and D2-transition of Rb atom;(b)dependence on the changed probe laser intensity for spin noise spectra of rubidium atomic gas with 250 Torr N2buf f er gas.

改变探测光功率I(从200µW增大至550µW),测量得到的自旋噪声谱如图3(b)所示.

如前文所述,自旋噪声谱包括两种贡献,其实验结果如图4所示.第一,背景噪声SBN即固有噪声(图2(a)中的背景高度),正比于光强,无光的情况下也存在固有噪声(图4(b)中拟合曲线在y轴上的截距),例如DAC的电路噪声;第二,自旋随机涨落带来的自旋噪声信号SSN,即图3的实验结果中85Rb和87Rb在不同探测光光强下的自旋噪声峰的峰高,正比于光强的平方.

将自旋噪声谱实验系统中平衡光桥探测器“两眼”接收到的光强分别表示为I1和I2,总光强为I.当光强为零时,探测器等产生的系统中固有噪声用S0来表示,则光电转换后得到的探测器电学信号S大小可表示为S∝α(I1−I2)+S0,其中α是探测器的光电转换系数.光电转换信号的平均值可表示

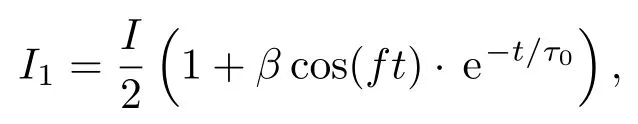
I2=I−I1,其中β为拉莫尔进动频率处的自旋噪声幅度,f为拉莫尔进动频率,τ0为自旋弛豫时间,且τ0≪T(T为单次采样时间),从而经过板卡上进行FFT取模平方的过程计算得到信号正比于光强的平方[20]:SSN∝α2β2I2(仅在频率f附近).

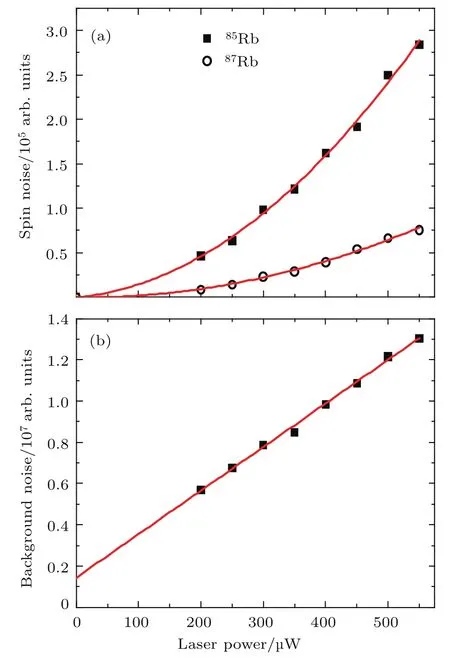
图4 (a)自旋噪声的贡献正比于探测光光强的平方;(b)背景噪声的贡献与探测光光强成正比Fig.4.(a)Spin noise signal shows square dependence on the changed probe laser intensity;(b)background noise is proportional to the intensity of the probe laser.

4.2 自旋噪声来自于自旋的随机涨落

为了进一步说明自旋噪声确实来自于自旋的随机涨落,在光路中起偏器的前面放置一个声光调制器(AOM),再进行自旋噪声谱的测量.所加横向磁场为B=13.8 G,声光调制器的频率f0=20 MHz,使用的样品2为充有100 mTorr N2的铷原子气,其他测量条件与之前的实验相同.在光路中加入声光调制器后,探测器光电转换后得到的信号表示为

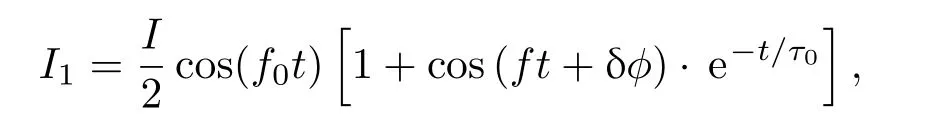
其中f0为声光调制器的频率,f为拉莫尔进动频率,δϕ表示涨落自旋的相对相位.如果δϕ是个随机量,求平均以后,其随机性仍然存在,就不会出现和频与差频(f0±f)的峰,只有f0和f的峰出现.实验结果确实如此(图5),说明自旋涨落是随机出现的.

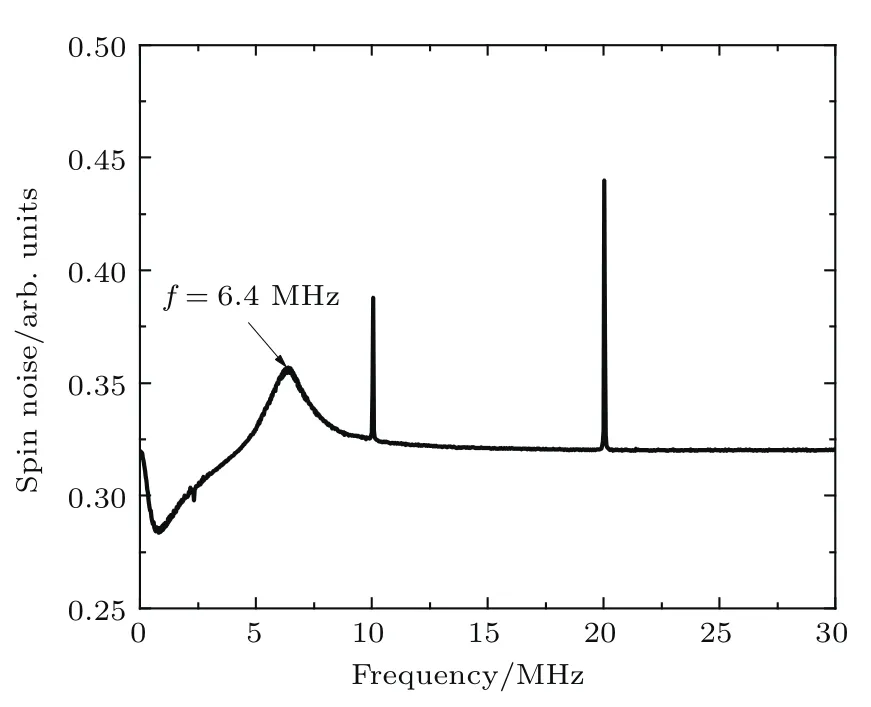
图5 在光路中加入声光调制器得到的自旋噪声谱Fig.5.Spin noise spectrum with AOM being inserted in the experimental system.

4.3 FFTsDAC2提高了信噪比和测量效率

先后设计了两种FFTsDAC(FFTsDAC1和FFTsDAC2),并对比其性能.二者的采样率都是1 GB/s(每秒钟采集1 GB的数据).值得说明的是,保证高采样率(1 GB/s)和实时傅里叶变换的前提下,自主设计并制作的采集卡的采样深度可达12 bit.FFTsDAC1的单次采样时间为32µs(每次采样32000个),而FFTsDAC2为128µs(每次采样128000个).根据采样定理可知,二者的频率分辨率分别为31.3 kHz和7.8 kHz,FFTsDAC2具有更高的采样精度和频率分辨率,FFTsDAC1和FFTs-DAC2的输入范围均为±0.5 V,采样深度N分别为8 bit和12 bit,则电压分辨率δVNbit=1/2N分别为4 mV和244µV.在数据传输上,FFTsDAC1使用USB2.0接口,FFTsDAC2是USB 3.0接口,最大传输带宽从60 MB/s提高到了500 MB/s.表1总结了FFTsDAC1和FFTsDAC2的典型参数.

表1 两种FFTsDAC的典型参数Table 1.Typical parameters of two kinds of FFTsDAC.

图6(a)给出了两种FFTsDAC在不同测量时间内SNR的变化,在相同的测量时间内,FFTs-DAC2相比FFTsDAC1的SNR提高了80%左右.从图6(b)中可以看出,对于FFTsDAC2,当累加次数为10000次时,测量效率达到最大值90%,而FFTsDAC1的测量效率只有FFTsDAC2的一半左右.

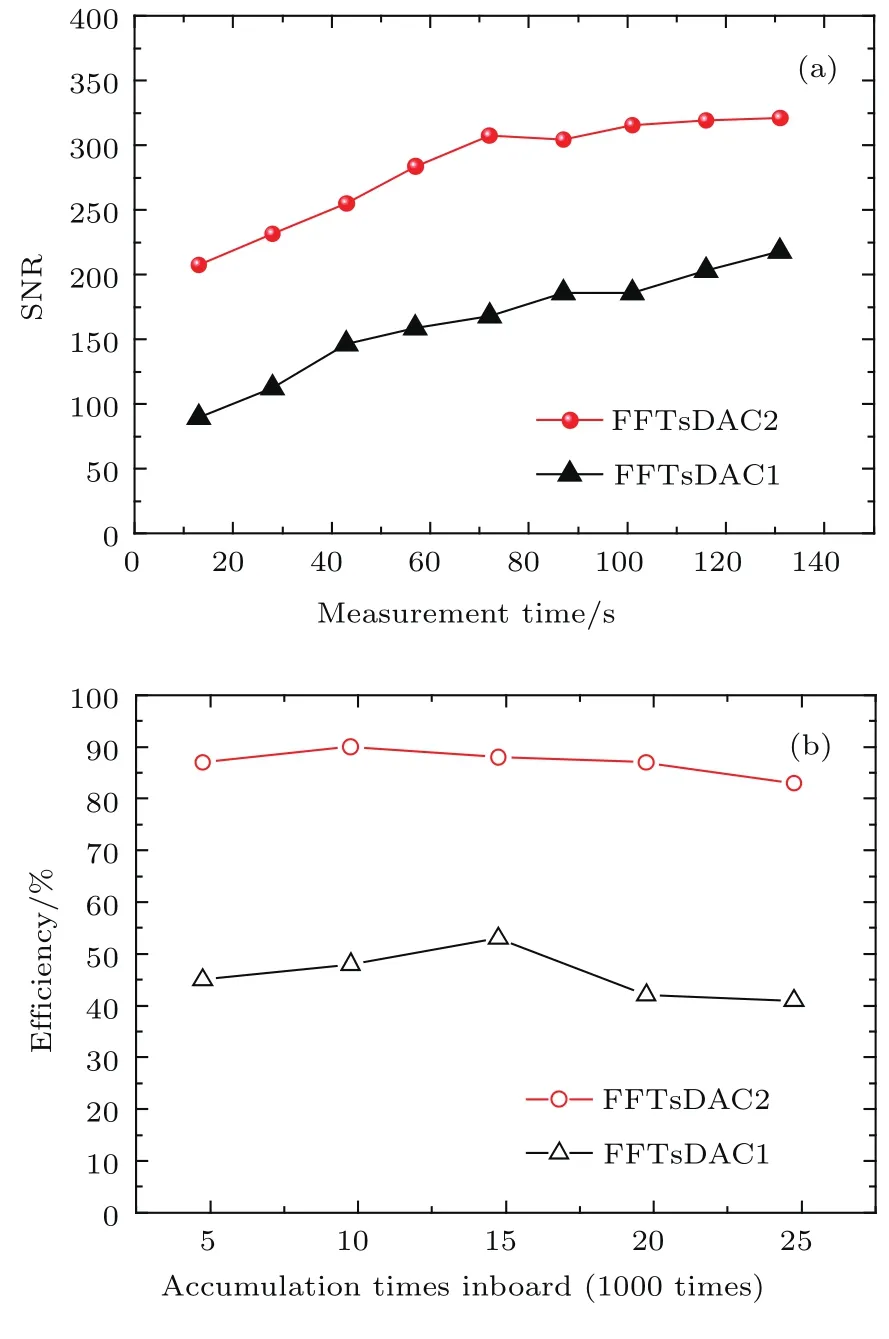
图6 FFTsDAC1和FFTsDAC2的 (a)SNR随测量时间的变化以及(b)测量效率对累加次数的依赖关系Fig.6.(a)Dependence of the SNR on the total measurement time and(b)dependence of measurement effciency on the accumulation time for FFTsDAC1 and FFTsDAC2,respectively.

4.4 不同频率分辨率对谱线半高宽的影响

自旋噪声谱中峰的半高宽反映的是自旋弛豫时间τ0=1/νFWHM[6].在测量中,会有很多因素影响谱线半高宽,这里主要考虑两个因素.一方面,原子的渡越时间以及采集卡采样时间的限制导致的截断效应.由于激光束的横截面积有限,同一原子在其自旋弛豫过程中无法始终处于探测光束之中.另一方面,因采集卡单次采样时间的限制,测量过程被强制终止,同样影响了自旋信号的相干性,导致测得的自旋弛豫时间更短.针对不同浓度缓冲气体的样品,影响自旋弛豫时间的因素不同[21].对于样品2低浓度缓冲气体的铷原子气样品,谱线半高宽受限于渡越时间;而对于样品1高浓度缓冲气体的铷原子气样品,分子和原子的碰撞作用较强,渡越时间不再是影响谱线半高宽的主要因素,而采集卡有限的采样时间将会截断信号的弛豫过程.为了研究截断效应对谱线展宽带来的影响,接下来的实验中采用高浓度缓冲气体的样品1(250 Torr N2的铷原子气)作为研究对象,将其置于8 G的横向磁场中,分别利用FFTsDAC1和FFTsDAC2进行自旋噪声谱测量,分析截断效应对谱线展宽带来的影响.

图7(a)中黑色和红色的线分别为FFTsDAC1的测量和拟合结果,测量和拟合所得谱线的半高宽均为64 kHz,对应的自旋弛豫时间约为15.6µs,这是因为FFTsDAC1单次采样时间较短(32µs),减少了采样点数,进行FFT后的频率分辨率较低(31.3 kHz),由此带来的截断效应更为明显.FFTs-DAC2所测得的自旋噪声谱结果如图7(b)所示,由于FFTsDAC2单次采样时间更长(128µs),具有更好的频率分辨率(7.8 kHz),测出的谱线半高宽更窄(48 kHz),对应的自旋弛豫时间约为20.8µs,一定程度上削弱了截断效应的影响,测量结果更为准确.

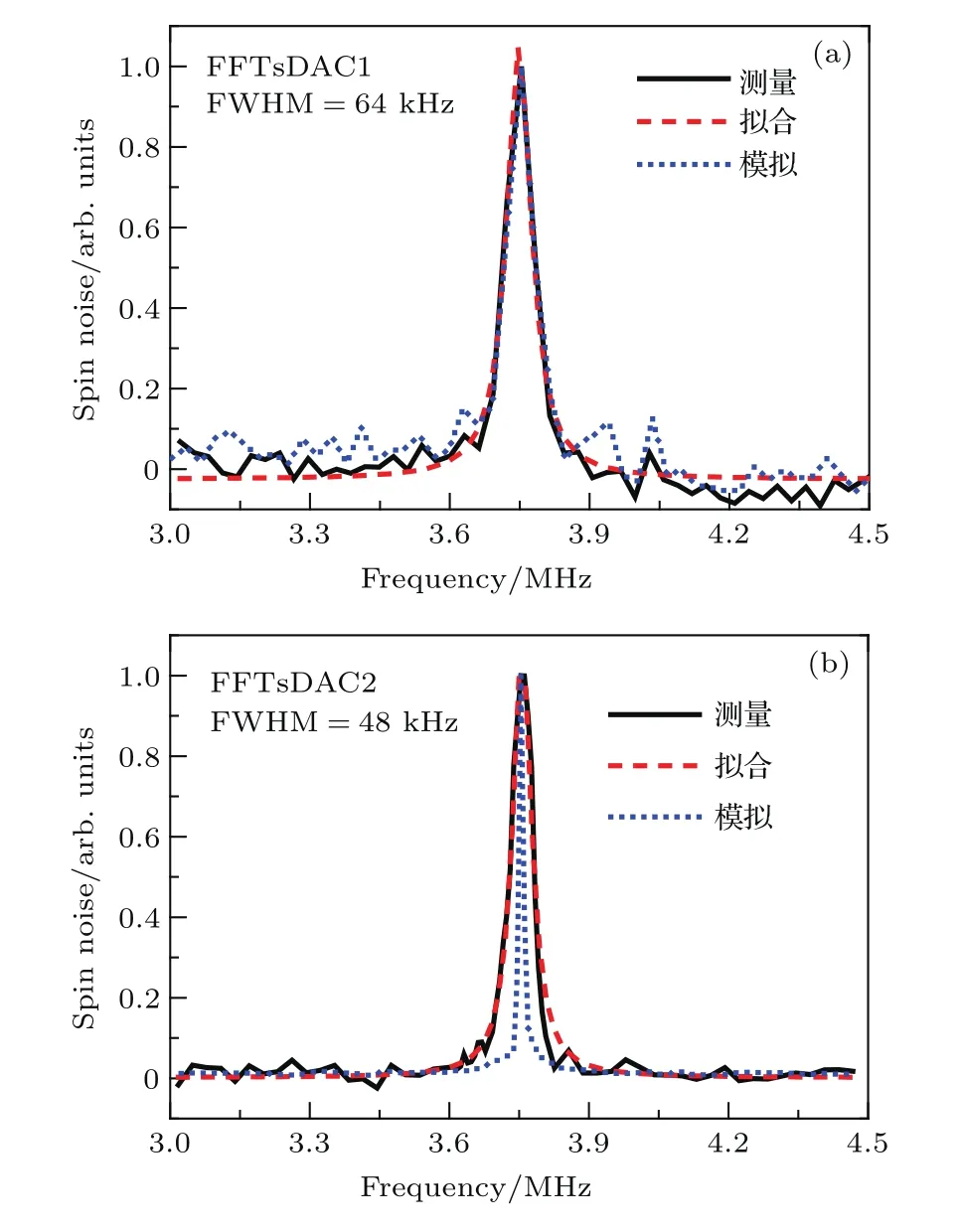
图7 充有250 Torr N2缓冲气体的铷原子气样品的自旋噪声谱测量、曲线拟合和数值模拟 (a)FFTsDAC1;(b)FFTsDAC2Fig.7. Comparison of measurement,fitting and simulation results of spin noise spectrum of rubidium atomic gas with 250 Torr nitrogen buf f er gas:(a)FFTsDAC1;(b)FFTsDAC2.

本文对频率分辨率不同的采样设备的自旋噪声测量过程进行数值模拟,其结果如图7中蓝色的点线所示.考虑一个寿命为200µs,振荡频率为3.7 MHz的振荡衰减信号,用其来模拟85Rb原子的电子自旋在8 G横向磁场下的拉莫尔进动过程.产生1000个相位及幅度均随机的进动衰减信号.模拟过程中所使用的两套与FFTsDAC1和FFTs-DAC2相对应的参数如下:采样率均为1 GB/s,有效的单次采样时间分别为32µs和128µs.从图7中可以看出,FFTsDAC1的拟合结果与实际测量结果符合得很好,这说明对信号峰半高宽的影响主要来自于较短的采样时间带来的截断效应.对于FFTsDAC2,模拟结果与实际测量相差较大,从模拟的结果可以验证理论上谱线半高宽仅受限于频率分辨率带来的展宽(16 kHz),对应的自旋弛豫时间约为62.5µs.而实际测量中得到的谱线更宽,说明FFTsDAC2影响谱线半高宽的不再是来自采集卡的截断效应,而是其他机理导致的谱线展宽,如外加磁场的不均匀性会为谱线带来一定程度的展宽.

5 结 论

介绍了自主搭建的自旋噪声谱探测系统及原理,以铷原子气系统自旋噪声的测量为例具体介绍了通过减去背景谱线的方法,对微伏量级微弱信号进行提取以及系统中固有噪声去除的过程.并且实验证实了自旋噪声确实来自于系统中自旋的随机涨落.研究了实验结果对探测光光强的依赖关系,发现自旋噪声谱测量系统的背景噪声与探测光光强成正比,而自旋噪声信号随探测光光强的增大以抛物线形式增大.对比了8 bit采样的FFTsDAC1和12 bit采样的FFTsDAC2的测量性能,分析了影响实验信噪比的因素.相比于FFTsDAC1,FFTs-DAC2单次采样时间长,节省了设备与电脑间的通讯时间,且采样精度高,减小了系统的噪声水平,从而具有更高的信噪比,而且其测得的谱线半高宽更窄、更准确,因为其具有更长的单次采样时间(更高的频率分辨率).分析了采样时间对自旋噪声峰的半高宽的影响,模拟了采样时间不同的采样设备的自旋噪声谱的测量过程,数值模拟结果与实验所得结果一致.

[1]Müller G M,Oestreich M,Römer M,Hübner J 2010Physica E43 569

[2]Crooker S A,Cheng L,Smith D L 2009Phys.Rev.B79 035208

[3]Aleksanfrov E B,Zapassky V S 1981JETP81 132

[4]Crooker S A,Rickel D G,Balatsky A V,Smith D L 2004Nature431 49

[5]Oestreich M,Römer M,Haug R J,Hägele D 2005Phys.Rev.Lett.95 216603

[6]Römer M,Hübner J,Oestreich M 2007Rev.Sci.Instrum.78 103903

[7]Crooker S A,Brandt J,Sandfort C,Greilich A,Yakovlev D R,Reuter D,Wieck A D,Bayer M 2010Phys.Rev.Lett.104 036601

[8]Müller G M,Römer M,Hübner J,Oestreich M 2010Appl.Phys.Lett.97 192109

[9]Quirk M P,Garyantes M F,Wilck H C,Grimm M J 1988IEEE Trans.Acoust.,Speech,Signal Processing36 1854

[10]Iglesias V,Grajal J,Sánchez A,Vallejo M L 2015IEEE Trans.Instrum.Meas.64 338

[11]Shi P,Ma J,Qian X,Ji Y,Li W 2017Acta Phys.Sin.66 017201(in Chinese)[史平,马健,钱轩,姬扬,李伟2017物理学报66 017201]

[12]Shannon C E 1949Proc.IRE37 10

[13]Demtröder W(translated by Ji Y)2012Laser Spectroscopy(4th Ed.,Vol.1)(Beijing: Science Press)pp162–163(in Chinese)[戴姆特瑞德 著 (姬扬 译)2012激光光谱学:(原书第四版第1卷)(北京:科学出版社)第162—163页]

[14]Horn H,Müller G M,Rasel E M,Santos L,Hübner J,Oestreich M 2011Phys.Rev.A84 043851

[15]Rubidium 85 D line data,Steck D A.http://steck.us/alkalidata[2018-1-10]

[16]Rubidium 87 D line data,Steck D A.http://steck.us/alkalidata[2018-1-10]

[17]Ma J,Shi P,Qian X,Li W,Ji Y 2016Chin.Phys.B25 117203

[18]Arimondo E,Inguscio M,Violino P 1977Rev.Mod.Phys.49 31

[19]Bize S,Sortais Y,Santos M S,Clairon A,Salomon C 1999Europhys.Lett.45 558

[20]Zhu Y S 2006Probability and Statistics in Experimental Physics(2nd Ed.)(Beijing:Science Press)pp431–433(in Chinese)[朱永生2006实验物理中的概率和统计(第二版)(北京:科学出版社)第431—433]

[21]Demtröder W(translated by Ji Y)2012Laser Spectroscopy(4th Ed.,Vol.1)(Beijing: Science Press)pp74–77(in Chinese)[戴姆特瑞德 著(姬扬 译)2012激光光谱学 (原书第四版第1卷)(北京:科学出版社)第74—77页]