广义模糊熵图像阈值分割参数选取的ADE方法

姜圣涛，穆学文

JIANG Shengtao,MU Xuewen

西安电子科技大学 数学与统计学院，西安 710126

School of Mathematics and Statistics,Xidian University,Xi’an 710126,China

1 引言

图像分割在图像分析和图像识别中具有很大作用，其研究一直受到学者们的广泛关注，尤其阈值分割方法在实际问题中应用十分广泛。

基于模糊熵的图像阈值分割[1]是一种常用的方法，模糊熵描述了一个模糊集的模糊性程度。传统的模糊熵使用了Zadeh[2]给出的模糊集上的标准正交、并和补运算，其中补运算为c()x=1-x，由于其不动点位于0.5处，再加上传统补运算不能与传统的模糊熵表达式建立起自然的联系，这就限制了它在很多实际工程中的应用。鉴于此西安邮电大学的范九伦教授给出了广义模糊熵方法[3]，广义模糊熵是模糊熵在广义模糊补[4]意义下的推广，用隶属度恒取m(0＜m＜1)时模糊集上的模糊熵最大取代模糊熵中隶属度恒取定值0.5，然后依据图像质量评价准则[5]，最终确定出最好的m，这样有一定的效果，但不能实现参数m的自动选取。目前研究者给出了部分优化算法应用于广义模糊熵图像分割，例如文献[6]给出的粒子群算法（Particle Swrarm Optimization，PSO），此方法对光照不均匀图像具有不错的分割效果，但对其他图像仍有局限性。

本文提出通过优化算法在(0,1)区间对m进行全局寻优，在图像分割时选用的隶属度函数是经典的S型函数[7]，它涉及到3个参数(a,b,d)的确定，采用自适应差分进化算法来求解，自适应地选取最优参数，以此来获得最优分割结果。本文将ADE算法应用于广义模糊熵图像阈值分割上，实验表明：多数情况下，针对不同的图像此方法能获得比文献[6]方法更好的分割效果，分割结果背景信息更少，目标信息更清晰，此方法不仅相对更具通用性，而且通过全局寻优来确定参数，克服了穷举搜索费时的缺点。

2 广义模糊熵阈值分割法

2.1 广义模糊熵定义

（3）若A*是A的分明修改，则，其中A*满足

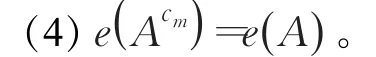
c表示广义补函数，使用最广泛的补函数是Zadeh[2]提出的基本补运算c()x=1-x，其特点是0.5是唯一不动点。广义补运算[4]中c具有唯一的不动点m，即。对于m∈(0,1)且以m为唯一不动点的补函数记作cm。当m=0.5,c0.5(x)=1-x时，上述定义即为传统模糊熵的表述。因此上述广义模糊熵定义是传统模糊熵的自然而合理的推广。

日本学者Sugeno曾给出了一个补函数[8]：

将式（2）带入式（1）得到Sugeno补[8]的等价变形为：

将式（3）代入如下广义模糊熵表达式即可得到含有参量m的广义模糊熵公式[9-10]，如式（4）所示：

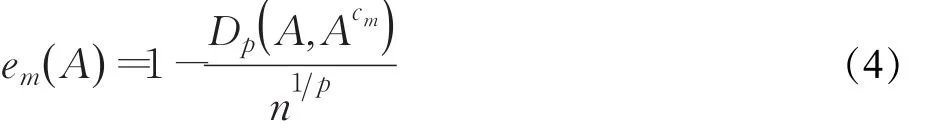
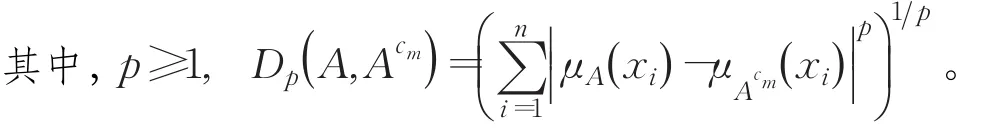
设Q={q(x,y),μQ(q(x,y)),x=1,2,…,M;y=1,2,…,N}表示大小为M×N的图像，G={0,1,…,L-1}表示图像所有灰度的集合是坐标处的像素灰度值表示(x,y)处像素在图像Q中具有某种特性的隶属函数。目前，在广义模糊熵方法中，通常采用如式（5）的S型函数[7]作为隶属度函数：

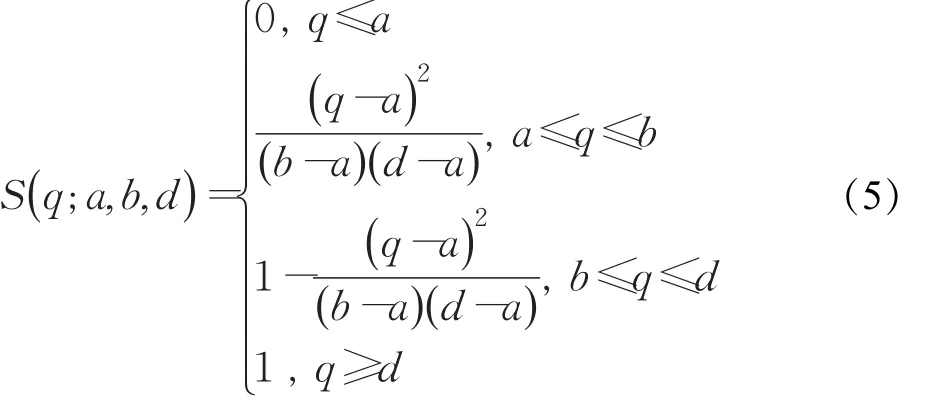
式中q表示图像Q的灰度值，a、b、d是S型隶属函数的3个参量，变化范围为：0≤a＜b＜d≤L-1，对每一组参量(a,b,d)可以求得对应的图像的广义模糊熵。然后根据最大广义模糊熵原则[3]对图像进行分割。该原则的内容是：在空间Ln（L为隶属度函数中参数的取值范围，n为隶属度函数中的参数个数，本文L的取值范围是[0，255]中任意整数值，n取值为3，搜索一组含n个参数的组合参数，使得图像在此参数确定的模糊划分下保留原图像的信息量最大。此时图像分割问题就是寻找使得广义熵取最大值的参数a、b、d的问题[3]，即：

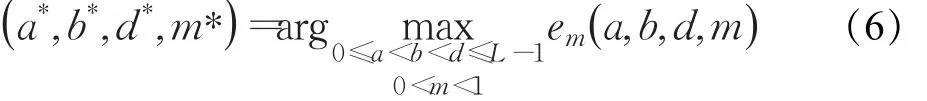
将式（6）所求的组合参数带入式（5）即可求得最佳阈值，即最优阈值选取在，获得图像分割阈值后，就可以对像素重新归类，得到分割后图像f(x,y)。

2.2 广义模糊熵参数确定

由上面的分析可知，广义模糊熵阈值分割法的分割阈值与一组参量相对应，如何寻找一组合适的参量使得广义模糊熵最大是确定阈值的关键。对于灰度图像，参量a、b、d的变化范围为0≤a＜b＜d≤L-1，且 a、b、d 仅取整数。这样寻找合适a、b、d的最简单方法就是穷举法，但这种方法运算量太大，时间复杂度过高(O(L4))。对于参量m，其取值为(0,1)区间上的任意实数，如何合理选取参量m，是使用广义模糊熵阈值化法最为关键的一步。

本文对参量的选取采用以下思路 ：利用优化搜索算法在参量空间搜索。搜索过程为嵌套的过程以广义模糊熵最大为准则在空间Ln寻找合适的参量a、b、d，同时以自适应差分进化（DE）为优化算法在（0，1）区间寻找最佳的参量m。

3 自适应差分进化算法

在利用广义模糊熵法进行图像阈值分割时，选取优化参数时的优化算法采用自适应差分进化算法，该算法基本原理步骤同差分进化算法（DE）[11-15]一致，不同点在于本文引入了自适应变异算子来代替基本差分进化算法中的变异算子F，还提出了交叉概率自适应函数，通过进化迭代步数动态改变交叉概率CR的值。通过以上操作，本文所提的自适应差分进化算法即是在差分进化算法基础上再添加自适应过程所得，因此必须先详细介绍差分进化算法。

3.1 差分进化算法

差分进化算法[11-15]是一种基于进化思想的最优化算法，具有记忆个体最优解和种群类信息分享的特点。它通过种群内个体之间互相合作和竞争来完成优化问题的求解，采用实数编码方式在整个解空间并行地搜索问题的解决方案，其基本执行过程同遗传算法一样，包括变异、交叉、选择等主要步骤。

设当前进化代数为t，群体规模为NP，个体长度为D，当前种群为为种群中的第i个个体。在进化过程中，对每个个体依次进行下面3种操作[16]。

（1）变异操作

（2）交叉操作

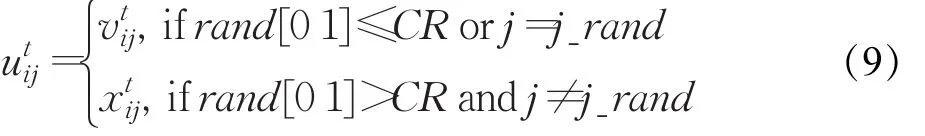
其中，rand[0,1]是[0,1]间的随机数；CR是交叉因子，取值区间为[0,1]，CR值越大，发生交叉的可能性就越大；j_rand是在[1,D]随机选择的一个整数，它保证了对于试验个体至少要从变异个体中获得一个元素。以上的变异操作和交叉操作统称为繁殖操作[17]。

（3）选择操作

其中，fitness()为适应度函数，一般以所要优化的目标函数为适应度函数。本文的适应度函数如无特殊说明均为目标函数且为求函数极小值。

3.2 自适应过程

DE算法在搜索过程中变异算子为实常数，若变异率过小，则种群多样性降低，易造成局部收敛，若变异率过大，则搜索效率低，所求的最优解精度就低，在实施中变异算子较难确定。选择适当的交叉概率也尤为重要，若交叉概率越高，群体中个体的更新就越快。但若是过高，算法就变成随机搜索失去优越性。反之交叉率过低，群体的进化得不到保证，很难收敛到最优解。为了采用自适应方法更新算法参数值来确定最优阈值，本文引入了一个自适应变异算子F'以及提出了交叉概率自适应函数CR，具体如下：

（1）引入自适应变异算子F'来替代基本差分进化算法中的变异算子F。

（2）提出CR自适应函数式（12）根据进化迭代步数动态改变CR的值。

其中，CR0为开始时交叉概率；CR1为交叉概率的稳定值；G为当前迭代步数；Gmax为最大迭代步数开始时交叉概率CR0比较小，随着进化的进行，个体开始逐步收敛，CR的值不断增大，变异个体基因选入新个体的概率也增大，则收敛速度不断提高，但很可能形成局部收敛。为防止局部收敛产生，当CR=CR1时，CR值不再增加保持稳定。

双自适应的目的是为了让算法的全局开发能力更强，自适应地控制F和CR的值在[ ]0,1内处于最佳，使进化参数在进化的不同阶段能够相互补充。因为在进化过程中每一个新个体如果F值没取最佳，值若偏大，尽管种群多样性提高但扰动量大，搜索步长在一个很大的范围内波动，从而降低局部搜索性能；值若偏小扰动量也小，使得新个体与基准个体变化不大，不利种群进化。如果交叉概率CR值不是最佳，值若较小，可能只有少数几维来自变异向量，不利于全局寻优；若值较大使得新个体与原个体相差太大，无法保证种群进化的有效性。因此将F和CR值控制在最佳状态这样才可以保障种群更加有效、迅速地向最优值进化，从而得到图像最优分割结果。

3.3 算法性能测试

不同缩放因子和交叉概率展示了相互不同的特性，本文期望参数在进化的不同阶段能够相互补充而不相互矛盾，则必须采用测试函数进行测试。鉴于大部分图像灰度直方图为多峰图，本文实验所选取的图像也皆为多峰图[18]，其直方曲线图见图1，所以可用经典适应度评价函数Griewank多峰函数[19]来测试算法性能。

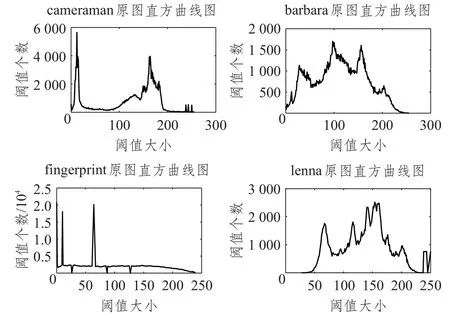
图1 实验原图直方曲线图

由于双自适应性存在，为平衡全局搜索能力和局部搜索能力以及避免参数出现矛盾的情况要对算法反复试验，代入多组数据，在迭代步数不是特别高的情况下，范围为，只要使交叉概率初始值CR0以及交叉概率的稳定值CR1选定合适值即可，反复试验可取CR0=0.3,CR1=0.9，具体测试过程参照文献[15]。

本文主要将文献[3]中传统图像质量评价准则模糊熵图像阈值分割算法以及文献[9]中PSO广义模糊熵图像阈值分割算法同本文所提出的ADE广义模糊熵图像阈值分割法来进行实验比较。文献[3]根据评价函数确定图像阈值不涉及进化迭代，因此为验证算法的收敛性只对比PSO法和ADE法迭代步数和适应度之间关系即可。

测试实验时对两种算法设置相同的操作参数，测试参数为：NP=100，CR0=0.3,CR1=0.9变异算子F和交叉算子CR的值依次按照自适应公式（11）式和（12）式来选取。避免参数相互矛盾进化代数不宜过大([1,1 000])，又测试样本不大，故可设定最大进化代数为Gmax=100，粒子位置限制在[0，255]之间，算法终止条件为，其中为全局最优个体xbest的适应值，f(Vi)为迭代终止前当代个体Vi的适应值，两种算法的进化曲线见图2。图像分割仿真实验时，根据所选图像样本大小，在范围内再重新设定最大迭代步数。

由图2可知，20代之前PSO法效果要略好于ADE法，尤其是10代之前收敛速度要略快于ADE法，但10代以后容易形成局部收敛，不利种群进化发展。20代后ADE法明显更好，并且随着进化代数的增大最终进化曲线达到收敛。总的来说PSO法尽管在10代以前收敛速度更快，但存在局部收敛并且在有限的迭代次数内无法达到收敛效果，ADE法在100代之内就可收敛，收敛效果良好，所以本文利用双自适应得到的算法整体上降低了局部收敛的几率，并且算法稳定性相对较好，收敛速度也相对较快。

图2 PSO和ADE算法进化曲线

4 ADE求广义模糊熵最优组合参数步骤

本文实验所选取的图像为灰度范围是0～255的二维灰度图像，为达到图像自动选取阈值的目的，首先对初始种群个体数NP进行编码，设个体长度为D，每个个体对应一条染色体，其向量为对应灰度计算值如式（13）：

ADE求广义模糊熵最优组合参数步骤为：

步骤1输入图片获取种群数NP，给出交叉概率初始值和稳定值CR0=0.3,CR1=0.9，以及个体长度D，变异算子F初值和交叉算子CR初值。指定变量搜索范围指定最大迭代次数Gmax，令迭代计数器G=1，进化代数t=0。

步骤3 WhileG≤Gmax//或其他指定终止条件。

步骤4 Fori从1到NP

步骤5 用式（11）生成F'取代F，令F=F'。

步骤6 IfCR＜CR1Then

根据式（12）得到新CR。

Else根据式（12）得到新CR。

End If

步骤10 End For

Else

迭代计数器G=G+1。

Return步骤3

步骤12 End While

步骤14将最优的参量组合代入式（6）得到最佳的图像分割阈值。

End

利用广义模糊熵对图像阈值分割最大的难点就在于如何求补函数的参数，本文采用自适应差分进化的算法来进行优化求解。对于256色灰度图像，一般的优化算法需要搜索256×256个候选阈值向量，算法运行效率非常低，自适应差分进化算法具有较好的寻优性能和效率，利用上述求解步骤得到最优解进而代入式（6）就可得到最佳的图像分割阈值。

5 实验结果与分析

为了检测算法的性能，在Matlab R2016a环境下进行仿真实验，处理器为Intel Core 2.30 GHz，运行内存为4 GB，选用cameraman.jpg、lenna.jpg、fingerprint.jpg和barbara.jpg这四种不同细节的图片进行实验，图片的尺寸均为252×252。分别采用传统图像质量评价准则模糊熵图像阈值分割算法[3]、PSO广义模糊熵图像阈值分割算法[9]以及本文所提出的ADE广义模糊熵图像阈值分割法来进行实验比较。

图3为实验所选取的四幅原图像，经过多次试验，由三种方法得到的四幅不同细节图像的最优参数组合以及最佳阈值见表1，三种算法的实验仿真结果见图4～图7，图表中所提到的算法1、算法2和本文算法依次为传统图像质量评价准则模糊熵图像阈值分割算法、PSO广义模糊熵图像阈值分割算法和本文的ADE广义模糊熵图像阈值分割法。

图3 原图像

由表1可看出：对于同一幅图像，本文算法所得的最优阈值同算法2所得到的最优阈值相近，这也从侧面验证了本文算法具有可行性。

由图4～图7可以看出：针对不同图像，对比各种算法分割效果，整体直观上算法2同本文算法所得结果背景信息更少，分割结果更加接近，这也同表1得到的最优阈值数值相近保持一致。算法1分割结果存在一定的背景信息且目标信息不是特别理想，算法2进行了很大的改良，而本文算法其分割所得目标中明显含背景信息更少且目标信息更清晰，大多数情况下效果更好。

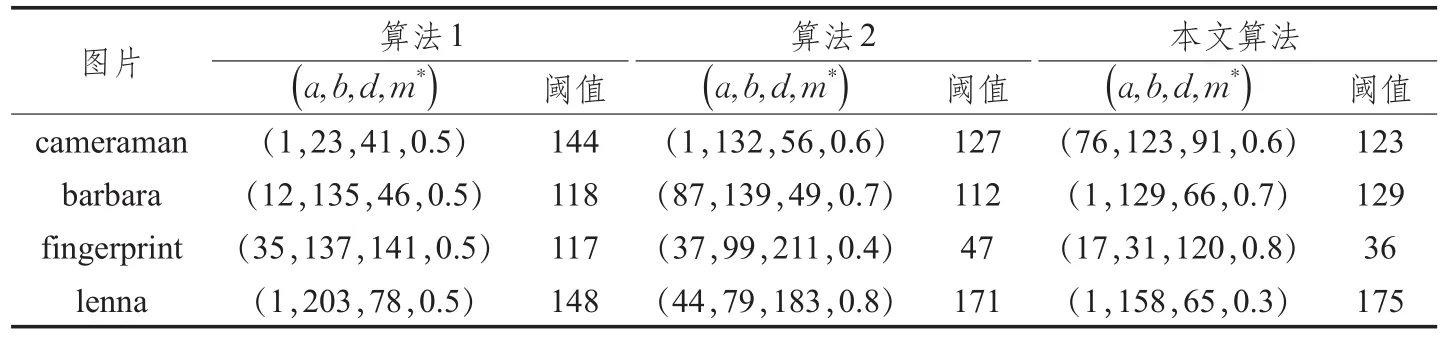
表1 三种算法得到的最优参数组合及阈值

进一步比对三种算法分割结果，由图4和图6可明显看出本文算法分割结果更好，这两类图像采用本文算法得到的结果背景信息较少且目标信息更清晰完善，其中图6中本文所得结果指纹纹理更清楚更平滑更接近目标信息；由图5和图7可看出 算法2和本文算法分割结果差异不是特别明显，通过对比还是本文算法分割所得背景信息更少，分割情况略好于算法2结果。同时发现，图7（b）和图7（c）中所得结果目标信息都有所丢失，比如lenna的嘴唇信息部分缺失，而图7（a）嘴唇信息却完整地保留下来了，但背景信息过多，整体上远远没有算法2和本文算法分割效果理想。对比发现：总体上利用本文算法大部分图像的分割结果还是比较理想的。这也说明了本文算法不能适用于所有类型的图像分割也存在一定的不足，但可以适用于多数图像。

图4 cameraman三种算法分割结果

图5 barbara三种算法分割结果

图6 fingerprint三种算法分割结果

图7 lenna三种算法分割结果

为了更定量比较几种算法分割效果的优劣，实验中除了比较算法运行时间外，再采用分类错误（Misclassification Error，ME）[20]来评价算法的优劣。分类错误ME的取值范围为[0，1]。ME取值越小，则分割错误越小，表明分割后图像的效果越接近理想分割。分类错误的计算公式[20]如下：

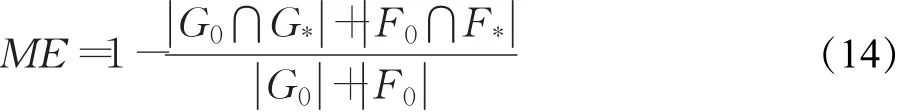
式中，G0和F0分别表示原图像中理想分割时的目标和背景区域，G*和F*分别表示分割后图像中的目标和背景区域。

表2给出了文中三种算法对实验中四幅图像分割后的分类错误以及算法运行时间。由表2可知，针对不同细节的图片本文算法整体运行时间较短，ME值除了lenna图像中算法2的为0.112略小于本文的0.129，其余均为本文算法ME值最小，这也定量地说明了整体上本文算法针对四种不同细节图片都有较好的结果，即本文算法适用性更广，并且能有效、稳定地找到一幅图像的最佳熵阈值进而进行分割。

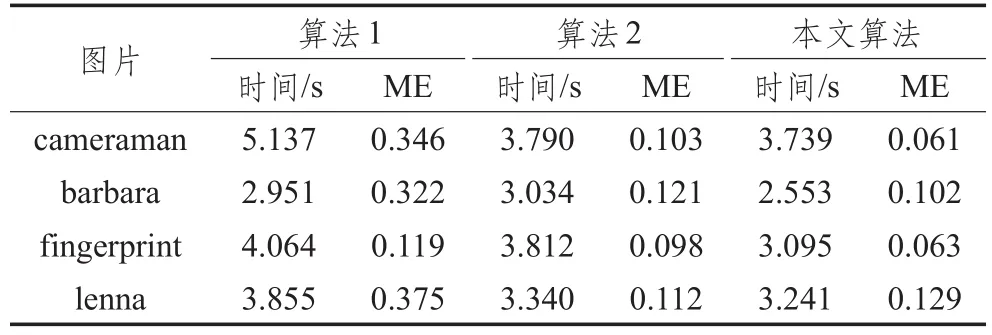
表2 三种算法ME值和运行时间

6 总结

由于图像来源千差万别，导致图像的细节具有多样性。迄今，尽管给出了一些研究成果，但目前尚无通用的分割理论提出，现已提出的算法大都是针对具体问题。本文在仿真实验时，也依然存在lenna图像目标信息有所丢失的状况，这也说明了本文算法同样不能适用于所有类型的图像分割。不过总体来说本文通过四种不同细节的图片进行仿真实验，结果也验证了本文所提出的算法具有良好的效果，间接说明了本文所给的算法相对实用性更广，实验证明此算法是一种较实用的阈值分割算法。

参考文献：

[1]符翔，张剑，王维.一种新的局部阈值分割算法[J].计算机应用与软件，2015，32（4）：195-198.

[2]Zadeh L A.Fuzzy sets[J].Information and Control，1965，8（3）：338-353.

[3]范九伦，赵凤.基于Sugeno补的广义模糊熵阈值分割方法[J].电子与信息学报，2008，30（8）：1865-1868.

[4]张旭慧，辛小龙.广义模糊熵与包含度的相互诱导关系[J].模糊系统与数学，2011，25（6）：16-22.

[5]雷博，范九伦.二维广义模糊熵图像阈值分割法[J].光子学报，2010，39（10）：1907-1914.

[6]张新娟，雷秀娟.改进PSO算法在二维最佳阈值图像分割中的应用[J].计算机工程与应用，2011，47（26）：207-209.

[7]Li H，Yang H S.Fast and reliable image enhancement using fuzzy relaxation technique[J].IEEE Transactions on Systems，Man and Cybernetics，1989，19（5）：1276-1281.

[8]Sugeno M.Fuzzy measures and fuzzy integrals：A survey[C]//Fuzzy Automata and Decision Processes，1977：89-102.

[9]雷博，范九伦.广义模糊熵阈值法中基于粒子群优化的参数选取[J].控制与决策，2009，24（3）：446-450.

[10]曾小浩，乔明明.基于组合优化算法的图像阈值分割[J].计算机应用与软件，2014，31（2）：207-210.

[11]刘波，王凌，金以慧.差分进化算法研究进展[J].控制与决策，2007，22（7）：721-729.

[12]汪慎文，张文生，丁立新.差分进化算法中参数自适应选择策略研究[J].计算机科学，2015，42（11）：256-259.

[13]高岳林，刘军民.差分进化算法的参数研究[J].黑龙江大学自然科学学报，2009，26（1）：81-85.

[14]张莉，叶志伟，王明威.基于差分进化的二维熵图像分割[J].应用科学学报，2016，34（1）：58-66.

[15]刘华，张营，张英杰.基于自适应差分进化算法的矾花图像分割[J].控制工程，2016，23（8）：1203-1207.

[16]林志毅，李元香.一种求解函数优化的混合差分演化算法[J].系统仿真学报，2009，21（13）：3885-3893.

[17]邓泽喜，刘晓冀.差分进化算法的交叉概率因子递增策略研究[J].计算机工程与应用，2008，44（27）：33-36.

[18]Griewank A O.Generalized descent for global optimization[J].Journal of Optimization Theory and Applications，1981，34：11-39.

[19]Tsai D M.A fast thresholding selection procedure for multimodal and unimodal histograms[J].Pattern Recognition Letters，1995，16（6）：653-666.

[20]Sezgin M，Sankur B.Survey over image thresholding techniques and quantitative performance evaluation[J].Journal of Electronic Imaging ，2004，13（1）：146-165.