一种新的自适应惯性权重混沌PSO算法

李龙澍，张效见

LI Longshu1，2,ZHANG Xiaojian2

1.安徽大学 计算智能与信号处理教育部重点实验室，合肥 230039

2.安徽大学 计算机科学与技术学院，合肥 230601

1.Key Laboratory of Intelligent Computing and Signal Processing,Anhui University,Hefei 230039,China

2.School of Computer Science and Technology,Anhui University,Hefei 230601,China

1 引言

PSO算法是一种寻优算法，于1995年由Eberhart和Kennedy首次提出[1-2]。它源于模拟鱼类和鸟类的寻食行为[3]。PSO算法具有操作简单、鲁棒性强和易于实现等优点，优化性能较好，常用于解决多峰值、不可微和非线性等问题，并在工程和科学领域得到广泛应用，如函数优化[4]、排列[5]和神经网络[6]等。

虽然PSO算法优化性能较好，但是在寻优求解进程中，不能很好地平衡粒子的搜索行为，存在易陷入局部极值的缺陷。对此，研究人员提出了诸多改进方法，主要分为以下两类：第一类是在PSO算法速度迭代公式中增加惯性权重ω，以更好地平衡粒子的搜索行为。近年来，研究人员对惯性权重进行了广泛研究[7-10]。例如，文献[7-8]提出惯性权重线性减少方法，以提高寻优性能，并被广泛应用，称之为标准PSO算法。但在该算法中，如果粒子在寻优初期搜索到的位置不够好，易陷入局部极值。文献[9-10]对惯性权重采用指数减少方法，减少了算法陷入局部极值的概率。另一类是引入其他优化方法，文献[11]在PSO算法中引入两种混沌优化策略，提高了收敛精度。文献[12]在PSO算法中引入GA算法的变异和交叉操作，提高了收敛性。基于以上研究，本文针对PSO算法易陷入局部极值的缺陷，提出了一种新的自适应惯性权重混沌PSO算法（a New Chaos Particle Swarm Optimization based on Adaptive Inertia Weight，CPSO-NAIW）。实验结果表明，CPSO-NAIW算法能有效避免陷入局部极值，提高算法性能。

2 PSO算法

PSO算法可具体表述如下：首先初始化种群粒子，然后每一个粒子通过追逐个体和群体极值位置，即粒子本身和整个粒子种群当前找到最优解的位置，来更新粒子的位置和速度，最后不断迭代直到找到在指定阈值的最优位置。在种群规模为M，解空间为D维的PSO算法中，设第i粒子个体和群体极值位置分别为Pi和G，在d维的位置和速度分别为xid和vid，xid和vid的更新公式如下：

3 CPSO-NAIW算法

介绍了惯性权重线性减少方法的缺点，然后提出了一种根据粒子与群体极值位置距离进行权重调整的方法，该方法更好地平衡了粒子的搜索行为，减少了算法陷入局部极值的概率，最后针对算法如何摆脱局部极值的问题，提出了一种基于混沌优化摆脱局部极值的方法，该方法通过引入混沌优化策略，在算法陷入局部极值时，对群体极值位置进行调整，以使粒子经历新的搜索邻域和路径，增加算法摆脱局部极值的可能。

3.1 自适应惯性权重

在PSO算法寻优迭代中，应用较多的是惯性权重线性减少方法，然而，PSO算法的寻优进程是非线性且十分复杂的，线性减少的方法变化过于单一，造成其对非线性、复杂寻优进程的调节和适应能力有限，易陷入局部极值。因此，本文提出了一种新的惯性权重自适应方法（New Adaptive Inertia Weight，NAIW），NAIW计算方法如式（3）所示。

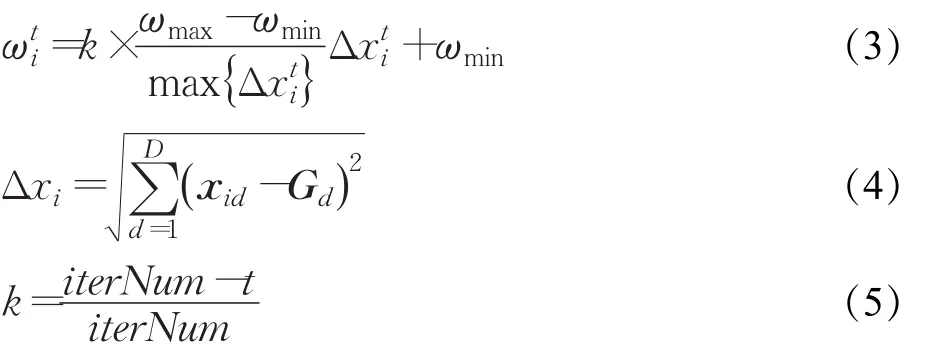
其中，ωmax和ωmin分别为惯性权重的最大和最小值，ωmax=0.9，ωmin=0.4[16]；Δxi为第 i个粒子与群体极值位置的距离，利用式（4）计算得到；为Δxi在t代中的值；iterNum为最大迭代次数；k为迭代系数，利用式（5）计算得到。NAIW方法通过粒子相对于群体极值位置的距离对权重进行动态调整，把权重的变化与粒子的位置状态信息关联起来，以更加精确地调整惯性权重。当较大时，即粒子距当前最优解位置的距离较远，则利用式（3）会赋予速度更新式（1）中较大的值，以使粒子获得较大飞行速度，进而可以使其更快速地向当前最优解位置靠近并保证了种群全局“探索”能力，当较小时，即粒子距当前最优解位置的距离较近，则利用式（3）会赋予速度更新式（1）中较小的值，以使粒子获得较小飞行速度，进而可以使其更加精细地搜索最优解位置邻域，保证了种群局部“开发”能力。同时，式（3）中的k值随迭代次数的增加而减少，以保证算法在迭代初期和后期分别对较大和较小的需要[7-8]。通过以上调整权重的方法，增强了权重的自适应性，更好地平衡了粒子的搜索行为，减少了算法陷入局部极值的概率，提高了PSO算法的收敛性。

3.2 基于混沌优化摆脱局部极值的方法

混沌是一种非线性的自然现象，具有随机性、遍历性等特点，可进行寻优搜索[17-19]。

一个常用的混沌模型Logistic方程如下：

其中，μ为控制参量，当 0≤z0≤1，μ=4时，Logistic处于完全混沌状态。式（7）为Logistic方程的一种演化形式[20]。

本文借鉴混沌现象随机性和遍历性的特点，提出了基于混沌优化摆脱局部极值的方法。该方法通过群体极值位置连续未更新的代数SG与局部极值判定阈值SGmax进行比较来判定算法是否陷入局部极值[14]。若SG≥SGmax，则认为算法已经或即将陷入局部极值；反之，则认为算法没有陷入局部极值。当算法被判定为陷入局部极值时，首先利用式（8）把群体极值位置G映射到混沌变量定义域[0,1]内，然后利用式（7）进行迭代运算，得到 M 个混沌位置(CG1,CG2,CG3,…,CGm)，最后利用式（9）进行逆映射，获得 M 个新群体极值位置（G1',G2',G3',…,Gm'）。由于粒子通过追逐个体和群体极值位置来完成自我更新，当算法陷入局部极值时，群体极值位置一定在局部极值位置上，此时，采用混沌映射得到具有较强随机性和遍历性的新群体极值位置，并结合式（1）就可以改变粒子的寻优轨迹，使得粒子i通过追逐新群体极值位置Gi'进行自我更新时，可在局部极值位置邻域外的其他区域进行寻优搜索，搜索新的邻域和路径。因此可以较大概率地发现更优解，进而增加了算法摆脱局部极值的可能。

3.3 CPSO-NAIW算法执行流程

本文从惯性权重的调整和如何摆脱局部极值两个方面对PSO算法进行改进，提出了CPSO-NAIW算法，该算法的具体执行流程如下。

输入：算法迭代次数T、种群规模M。

输出：最优位置G。

（1）随机初始化种群中粒子的速度和位置，初始化迭代次数、计数器和局部极值判定阈值为t=0、SG=0和SGmax=10[14]。

（2）初始化P为粒子当前位置，G为初始群体最优粒子位置。

（3）对种群中所有粒子执行以下操作：

②根据式（1）和式（2）更新粒子速度和位置。

③计算粒子适应度值 f，并更新粒子的P和G，如果G未更新，SG=SG+1，否则SG=0。

（4）如果 SG≥SGmax，利用式（7）～（9）对 G 进行混沌优化生成G1',G2',Gi',…,Gm'，SG=0。

（5）t=t+1，如果 t＜T ，转（3），否则，执行（6）。

（6）输出G，算法结束。

在CPSO-NAIW算法中，第（1）、（2）步对算法各个参数进行初始化，第（3）～（6）步对求解问题进行寻优搜索。其中，第（3）步利用本文提出的新惯性权重自适应方法（NAIW）对粒子进行更新，第（4）步判断算法是否陷入局部极值，若SG≥SGmax，则认为算法已经或即将陷入局部极值，并利用本文提出的基于混沌优化摆脱局部极值的方法来进行摆脱。

4 实验结果与分析

首先介绍了实验环境和算法参数设置，然后为了验证本文提出的改进方法的有效性，采用6个经典基准函数对算法性能进行测试。基准函数信息见表1。并设计如下方案进行对比。方案1：对两种改进方法分开进行测试，首先在标准PSO算法[7]（Standard Particle Swarm Optimization，SPSO）即线性减少惯性权重PSO算法的基础上，对权重的调整采用本文提出的新自适应惯性权重方法，形成PSO-NAIW算法，然后在SPSO算法基础上，加入本文提出的基于混沌摆脱局部极值方法，形成CPSO算法，最后把本文提出的两种改进方法综合起来，形成CPSO-NAIW算法并把它们与SPSO算法进行对比测试。方案2：为展示本文CPSO-NAIW算法的先进性，将CPSO-NAIW算法与一些具有代表性的新近改进PSO算法，即IAW-PSO[21]、高速收敛PSO算法（表示为FPSO）[14]、PDNPO-PSO算法[22]和SPSO算法进行对比测试。

表1 基准函数

4.1 实验环境与参数设置

实验采用C#编写，实验环境为（M490）CPU 3.20 GHz Inter core i5和4 GB RAM。PSO-NAIW、CPSO、CPSONAIW以及SPSO算法参数设置如下：惯性权重最大和最小值分别为ωmax=0.9和ωmin=0.4；IAW-PSO算法参数设置如下[21]：惯性权重最大和最小值分别为ωmax=0.9和ωmin=0.2；迭代步数K1=60，K2=10；最大初始化次数kmax=200；FPSO算法参数设置如下[14]：惯性权重最大和最小值分别为ωmax=0.9和ωmin=0.4；停滞上限MAX=10；PDNPO-PSO算法参数设置如下[22]：惯性权重最大和最小值分别为ωmax=0.9和ωmin=0.4；惯性权重取值范围中间值ωs=0.65；上限控制参数k1=2；调节能力控制参数k2=1；个体学习因子的最大和最小值分别为c1max=2和c1min=0；群体学习因子的最大和最小值分别为c2max=2和c2min=0；振荡周期L=300。所有算法的种群规模M为30；学习因子c1=c2=2。

4.2 PSO-NAIW、CPSO、CPSO-NAIW和SPSO算法对比测试

为了测试PSO-NAIW、CPSO和CPSO-NAIW算法性能，本文设置以下实验进行对比分析。

实验1 PSO-NAIW、CPSO、CPSO-NAIW和SPSO算法在迭代1 000次的情况下，对6个基准函数进行寻优搜索，每个算法进行20次独立实验，取各个函数最终结果的平均（Mean）和最优（Opt）值进行比较。实验结果如表2所示。

实验2 PSO-NAIW、CPSO、CPSO-NAIW和SPSO算法在固定目标精度下（各个函数目标精度如表1），对6个基准函数进行寻优搜索，每个算法进行20次独立实验，取各个算法达到目标精度时的平均迭代次数(Itr)、平均运行时间(t)及收敛率(CR)。其中，收敛率=达到目标精度次数/总实验次数。算法2 000次迭代内不收敛即视为当次实验失败，实验结果如表3所示。

从表2中看出，虽然PSO-NAIW、CPSO和CPSONAIW算法在对函数 f4和 f5测试时，与SPSO算法实验结果相同，但是在其他4个函数上无论是最优还是平均函数值都明显优于SPSO算法，并且CPSO-AIW算法实验结果最优。从表3中看出，虽然PSO-NAIW、CPSO和CPSO-NAIW算法在对函数 f1～f5测试时，与SPSO算法的收敛率相同，但是PSO-NAIW和CPSO算法对于除函数 f4外的其他4个函数，收敛速度更快、用时较少，并且，CPSO-NAIW算法对函数 f1～f5的收敛速度最快、用时最少。同时在表3中还可以看出，PSO-NAIW、CPSO和CPSO-NAIW算法在对函数 f6进行测试时，这三种算法相对于SPSO算法的收敛率更高、收敛速度更快、运行时间更短，并且CPSO-NAIW算法的收敛率最高、收敛速度最快、运行时间最短。综上，可以得出，PSO-NAIW、CPSO和CPSO-NAIW算法在整体性能上优于SPSO算法。这是因为PSO-NAIW算法根据粒子与群体极值位置距离来调整惯性权重，改善了权重的自适应性，更好地平衡种群的局部“开发”和全局“探索”能力，降低了算法陷入局部极值的可能。所以，算法用时较少、收敛精度和速度明显提高。CPSO算法利用混沌现象随机性及遍历性的特点，在算法陷入局部极值时，对群体极值位置进行混沌优化，以使粒子搜索局部极值外的新邻域和新路径，增强了算法跳出局部极值的可能。所以，算法运行时间短、收敛精度高且速度快。而CPSO-NAIW算法综合了PSO-NAIW和CPSO算法的改进方法，所以具有最优的收敛性能。

表2 实验1结果

表3 实验2结果

4.3 CPSO-NAIW、IAW-PSO、FPSO、PDNPOPSO和SPSO算法对比测试

为了验证本文CPSO-NAIW算法性能，在6个基准函数上对本文CPSO-NAIW与IAW-PSO、PDNPO-PSO、FPSO和SPSO算法进行20次独立实验，每次实验迭代1 000次。实验结果如图1～6所示。由图1～3可知，对于函数 f1～f3，本文CPSO-NAIW算法不仅求解精度高且收敛速度快。由图4和图5可知，本文CPSO-NAIW算法对函数 f4和 f5的求解都达到了相应理论极值，并且对于函数 f5，本文CPSO-NAIW算法收敛速度更快。由图6可知，虽然5种算法对于函数 f6求解效果都不理想，但是本文CPSO-NAIW算法的求解精度和收敛速度明显优于其他4种算法。因此本文提出的CPSO-NAIW算法具有很好的收敛性能。

图1 f1函数

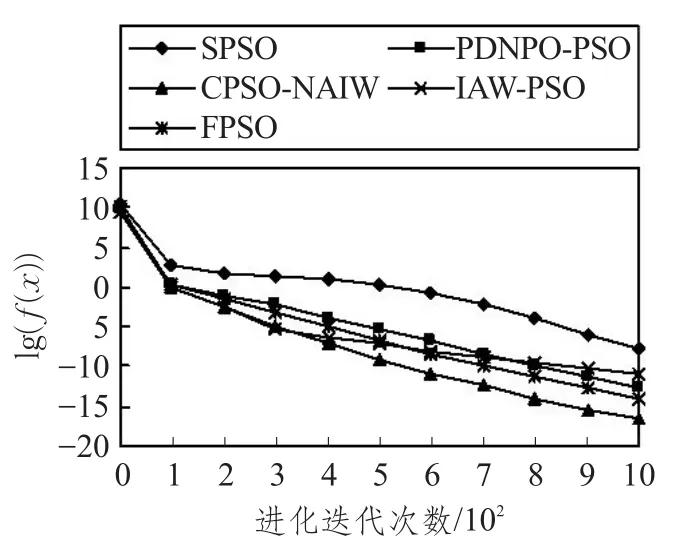
图2 f2函数

图3 f3函数

图4 f4函数

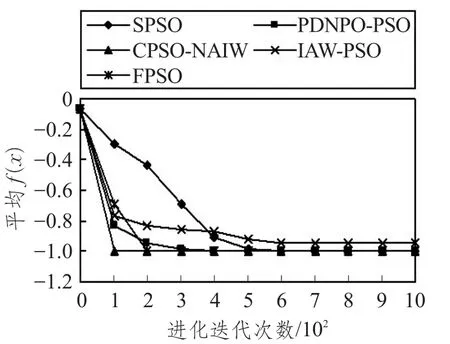
图5 f5函数

图6 f6函数

5 结论

本文针对PSO算法易陷入局部极值的缺陷，提出了一种新的自适应惯性权重混沌PSO算法（CPSO-NAIW）。该算法首先采用新的权重自适应方法（NAIW），通过粒子与群体极值位置距离对权重进行调整，使权重的调整与粒子的状态位置状态信息相结合，更好地平衡粒子的全局和局部搜索行为，在提高算法自适应性的同时减少了其陷入局部极值的概率，然后采用基于混沌优化摆脱局部极值的方法，该方法在算法陷入局部极值时，对群体极值进行混沌调整，以使各个粒子在追逐不同群体极值位置进行更新时，可以改变寻优轨迹，提高了算法摆脱局部极值的能力。实验结果表明，本文CPSO-NAIW算法，克服局部极值的能力更强，在收敛性能上更优。然而，本文CPSO-NAIW算法存在着稳定性不足问题，后续工作会针对该问题进行相关研究。

参考文献：

[1]Zhang Y，Gong D W，Ding Z.A bare-bones multi-objective particle swarm optimization algorithm for environmental/economic dispatch[J].Information Sciences，2012，192（6）：213-227.

[2]汤可宗，柳炳祥，杨静宇，等.双中心粒子群优化算法[J].计算机研究与发展，2012，49（5）：1086-1094.

[3]Nickabadi A，Ebadzadeh M M，Safabakhsh R.A novel particle swarm optimization algorithm with adaptive inertia weight[J].Applied Soft Computing，2011，11（4）：3658-3670.

[4]陈得宝，赵春霞.阶梯型粒子群算法及在函数优化中的应用[J].系统仿真学报，2007，19（24）：5659-5662.

[5]Goudos S K，Rekanos I T，Sahalos J N.EMI reduction and ICs optimal arrangement inside high-speed networking equipment using particle swarm optimization[J].IEEE Transactions on Electromagnetic Compatibility，2008，50（3）：586-596.

[6]Bashir Z A，El-Hawary M E.Applying wavelets to shortterm load forecasting using PSO-based neural networks[J].IEEE Transactions on Power Systems，2009，24（1）：20-27.

[7]Shi Y，Eberhart R C.Empirical study of particle swarm optimization[C]//Proceedings of the Congress on Evolutionary Computation，1999：32-49.

[8]Eberhart R C，Shi Y.Comparing inertia weights and constriction factors in particle swarm optimization[C]//Proceedings of the Congress on Evolutionary Computation，2000：84-88.

[9]Pediwal J，Mahor A，Khatri N.Exponential decreasing inertia weight particle swarm optimization in economic load dispatch[J].International Journal of Engineering Innovations&Research，2012，1（5）：380-384.

[10]Ting T O，Shi Y，Cheng S，et al.Exponential inertia weight for particle swarm optimization[C]//International Conference in Swarm Intelligence，2012：83-90.

[11]刘道华，原思聪，兰洋，等.混沌映射的粒子群优化方法[J].西安电子科技大学学报：自然科学版，2010，37（4）：764-769.

[12]雷秀娟，付阿利，孙晶晶，等.改进PSO算法的性能分析与研究[J].计算机应用研究，2010，27（2）：453-458.

[13]丁旭，吴晓蓓，黄成.基于改进粒子群算法和特征点集的无线传感器网络覆盖问题研究[J].电子学报，2016，44（4）：967-973.

[14]朱海梅，吴永萍.一种高速收敛粒子群优化算法[J].控制与决策，2010，25（1）：20-24.

[15]吕振肃，侯志荣.自适应变异的粒子群优化算法[J].电子学报，2004，32（3）：416-420.

[16]敖永才，师奕兵，张伟，等.自适应惯性权重的改进粒子群算法[J].电子科技大学学报，2014，43（6）：874-880.

[17]Ying Song，Chen Zengqiang，Yuan Zhuzhi.New chaotic PSO-based neural network predictive control for nonlinear process[J].IEEE Transactions on Neural Networks，2007，18（2）：595-601.

[18]Zhou Keliang，Qin Jieqiong.PID controller parameters tuning of main steam temperature based on chaotic particle swarm optimization[C]//IEEE International Conference on Computer Science and Automation Engineering（CSAE），2011：647-650.

[19]唐贤伦，周维，张衡，等.一种基于多目标混沌PSO的机器人足球防守策略[J].系统仿真学报，2014，26（1）：51-55.

[20]莫愿斌，陈德钊，胡上序，等.混沌粒子群算法及其在生化过程动态优化中的应用[J].化工学报，2006，57（9）：2123-2127.

[21]杜继永，张凤鸣，李建文，等.一种具有初始化功能的自适应惯性权重粒子群算法[J].信息与控制，2012，41（2）：165-169.

[22]朱喜华，李颖晖，李宁，等.基于群体早熟程度和非线性周期振荡策略的改进粒子群算法[J].通信学报，2014，35（2）：182-189.