区间二元语义Bonferroni集成算子及其决策应用

张茂竹，陈华友，韩 冰，江 莹

ZHANG Maozhu,CHEN Huayou,HAN Bing,JIANG Ying

安徽大学 数学科学学院，合肥 230601

School of Mathematical Sciences,Anhui University,Hefei 230601,China

1 引言

多属性决策过程就是决策者对若干方案的决策信息进行建模和择优[1]。在实际的决策过程中，由于人类思维的模糊性[2]以及客观世界的复杂性、不确定性，决策者对事物的评价往往以语言信息的形式给出。目前，已有一些文献[3-6]提出了若干语言信息集成算子的概念。文献[3]提出二元语义的Heronian平均算子和运算法则；文献[4]利用合作对策的方法探讨了语言信息的群决策模型。文献[5]给出广义语言有序加权对数平均算子的概念；文献[6]定义了语言环境下的广义Power算子。但是随着研究的不断深入，人们发现语言评价信息的集成结果往往会超出语言术语集的范围，从而在不同程度上造成了信息的丢失，进而导致决策结果不够精确。为了克服语言信息在运算过程中信息丢失的缺陷，Herrera[7]把语言术语变量通过一个表达式化为等价的二元语义信息。文献[8]提出二元语义信息集结的有序加权平均算子和有序加权几何平均算子的概念，并证明了该算子的数学性质，文献[9]利用二元语义OWA算子集结不同粒度语言判断矩阵的应用于语言偏好形式群决策信息，文献[10]拓展幂平均（PA）算子到二元语义信息环境，提出多种二元语义PA算子及其有序加权形式。文献[11-12]在Choquet积分和二元语义基础上提出了广义二元关联平均算子以及相应的诱导集成算子。考虑到在信息集成的过程中各属性两两之间的相互影响，文献[13]给出了二元语义Bonferroni平均算子和组合加权形式的算子的概念。

在运用语言信息进行评价的过程中，由于受到各种主客观因素的制约，决策者所给出的语言评价信息往往介于两个语言评价值之间，为此需要研究区间二元语义信息的集成方法和不确定的决策应用。针对这种情况，本文将二元语义Bonferroni平均（2TLBA）算子推广到区间二元语义的情形，提出了区间二元语义值Bonferroni平均（I2TLBA）算子及其加权平均形式，并提出了组合形式区间二元语义值加权Bonferroni平均算子，并讨论了它们的性质和几种特殊情况，并给出了基于C-I2TLWBA算子的多属性群决策模型、步骤和应用实例。

2 基本概念

定义2.1[14]称为语言术语集，其中si为具体的语言术语，i=1,2,…,g，g为偶数，S中元素的数目g+1称为语言术语集的粒度，记为||S=g+1。

通常，语言术语集S应满足如下性质：

（1）有序性：若 i≥j，则 si≥sj。

（3）存在极大化和极小化运算：若si≥sj，则

例如，一个粒度为9的语言术语集可表示为：

S={s0=极差，s1=非常差，s2=很差，s3=差，s4=中等，s5=好，s6=很好，s7=非常好，s8=极好}。

语言术语集在信息集成过程中容易造成信息的损失，为此引入二元语义的概念[7]。

定义2.2[7]设实数为二元语义信息集，则称函数为二元语义转换函数，即，其中β由下式确定：

其中round为取整算子，si∈S,α称为符号转移值。

反之，二元语义转换函数Δ的反函数Δ-1：S×可以将二元语义符号转化为实数信息，即

显然，对于任意的语言评价短语si∈S，均可将其直接转化成二元语义值，即：si=(si,0)。

（2）若 i=j，那么：

（1）若 i＞j，则

在实际的决策过程中，决策者给出的属性评价结果往往介于两个语言评价值之间，为此引入如下概念：

定义2.3[15]令S={s0,s1,…,sg}为语言术语集，若，且满足：

为了对两个区间二元语义值进行排序择优，下面给出其大小比较的可能度定义。

定义2.4[16]设为两个区间二元语义值，则的可能度为：

定义 2.5[16]设为两个区间二元语义值，关于区间二元语义的比较有如下结果：

（2） 当且仅当

Bonferroni平均的特点是在信息集成的过程中考虑到数据之间的相互影响，其定义如下：

定义2.6[17]设 p,q≥0，且实数集合满足ai≥0，i=1,2,…,n，若

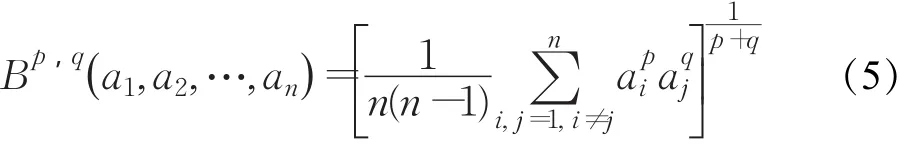
则称函数B为Bonferroni平均算子。

3 区间二元语义Bonferroni集成算子的概念及性质

为了对区间语言变量进行有效集成，有必要提出新的信息表达形式的集成算子。

定义3.1设

为一组区间二元语义值，若

则称I2TLBAp,q为区间二元语义Bonferroni平均算子，其中 p,q≥0。

根据定义3.1的式（6），容易证明，I2TLBA算子具有下述性质。

性质3.1（幂等性）若n个区间二元语义值均相等，即：

则有：

性质3.2（单调性）设两个区间二元语义值满足：

则有：

下面介绍几种I2TLBA算子的特殊情况。

则I2TLBAp,0算子简化为区间广义二元语义平均算子。则I2TLBA2,0算子简化为区间二元语义平方平均算子。

则I2TLBA1,0算子简化为为区间二元语义平均算子。

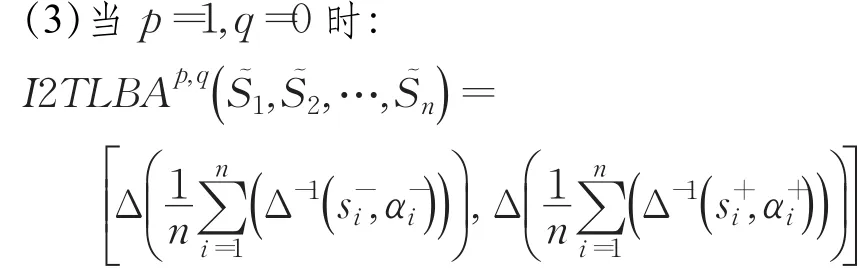
（4）当 p=1,q=1时：

则I2TLBA1,1算子简化为区间二元语义相关平方平均算子。

考虑到被集结的区间二元语义信息具有不同的重要性程度，现对I2TLBA算子进行推广，为此引入加权形式的算子。

4 组合形式的区间二元语义值加权Bonferroni平均算子

I2TLWBA算子应用的范围是集成n维区间二元语义值，群决策需要集成多组相应的数据信息，为此提出新的算子概念。

定义4.1设

为t组二元语义值，若

则称C-I2TLWBAω,λ为组合形式区间加权二元语义值的Bonferroni平均算子，记为C-I2TLWBA算子。其中ω=为加权向量中第 k大的元素，这里 λ=(λ1,λ2,…,λt)T是相应的权重向量t称为平衡因子。

模糊语义量化算子[18]给出加权向量的求法。C-I2TLWBA算子既考虑了区间二元语义值的重要性，又考虑了所在位置的重要性。

5 基于C-I2TLWBA算子的群决策方法

在不确定语言环境中，考虑到各个属性之间的相互影响，各个属性以及决策者均具有不同的重要性，在基于I2TLWBA算子和C-I2TLWBA算子的基础之上，提出了如下多属性群决策模型和步骤。

多属性群决策问题可以描述为：设X={X1,X2,…,Xm}为备选方案集，u={u1,u2,…,un}为属性集，w=(w1,w2,…,wn)T为属性权重向量，属性ui所对应的重要性程度为wi，满足为专家集合为专家的权重向量，满足。专家dk∈D给出方案Xi∈X在属性uj下的偏好关系为，从而专家 dk给出的决策矩阵为，其中 i=1,2,…,m;j=1,2,…,n ；k=1,2,…,t。

步骤3利用C-I2TLWBA算子对k位专家给出的决策方案的综合属性值进行集成，得到方案Xi的二元语义群体评价值。满足ωk∈[ ]0,1，中第k大的元素。

6 实例分析

设某足球队中有5名后备球员，由于主力球员受伤，现在想从5名球员中选择1名球员去参加比赛，用来表示5名球员，在对5名球员进行综合评估时，所要考虑的属性有u1（技术），u2（经验），u3（心理），u4（伤病），用 U={ }u1,u2,u3,u4表示。现请3位专家D={ }d1,d2,d3对5位球员进行评估，专家对球员的评价用下面的决策矩阵表示。设语言术语集为：

{s0=极差，s1=非常差，s2=很差，s3=差，s4=中等，s5=好，s6=很好，s7=非常好，s8=极 }好。

下面利用本文提出的方法对备选方案进行排序择优：

步骤1将区间决策矩阵化为区间二元语义决策矩阵，得：

步骤2令 p=1,q=1，利用I2TLWBA算子进行集成

步骤3利用C-I2TLWBA算子对3位专家的意见进行集成，专家的权重为，根据模糊语义量化算子“大多数”[18]，可得，则有：

步骤4根据式（4），对每个方案的二元语义群体评价值利用区间二元语义可能度公式进行排序，从而有：

因此，第一名球员为最合适的替补人选。

7 结束语

本文给出了区间二元语义Bonferroni平均算子及其相应的加权平均形式、组合平均形式的算子的若干概念，探讨了它们的一些重要的性质。Bonferroni平均算子可以考虑信息之间的相互关系，能有效地利用信息。

在不确定语言环境下的区间二元语义的多属性群决策信息的集成为区间二元语义Bonferroni组合平均形式的算子提供了很好的应用领域。基于区间二元语义信息后备球员的评价实例表明所构建的模型和方法是合理有效的。

在不确定语言环境下，除了Bonferroni平均算子可以考虑信息之间的相互关系之外，未来可进一步研究相应的Power平均算子和Heronian平均算子，并有必要研究他们各自的特点和适用范围。

参考文献：

[1]陈华友，陈启明，王慧.基于相对熵的不确定性群决策方法[J].安徽大学学报：自然科学出版社，2008，32（1）：1-5.

[2]彭祖明，陈义华.Vague集相似度量的一个新模型[J].安徽大学学报：自然科学出版社，2013，37（5）：12-16.

[3]Liu X，Tao Z F，Chen H Y，et al.A MAGDM method based on 2-tuple linguistic heronian mean and new operational laws[J].International Journal of Uncertainty，Fuzziness and Knowledge-Based Systems，2016，24（4）：593-627.

[4]Tao Z F，Liu X，Chen H Y，et al.Group decision making with fuzzy linguistic preference relations via cooperative games method[J].Computers&Industrial Engineering，2015，83（C）：184-192.

[5]Liu J P，Chen H Y，Zhou L G，et al.Generalized linguistic ordered weighted hybrid logarithm averaging operators and applications to group decision making[J].International Journal of Uncertainty Fuzziness and Knowledge-Based Systems，2015，23（3）：421-442.

[6]Zhou L G，Chen H Y.A generalization of the power aggregation operators for linguistic environment and its application in group decision making[J].Knowledge-Based Systems，2012，26（2）：216-224.

[7]Herrera F，Martinez L.A 2-Tuple fuzzy linguistic representation model for computing with words[J].IEEE Transactions on Fuzzy Systems，2000，8（6）：746-752.

[8]姜艳萍，樊治平.二元语义信息集成算子的性质分析[J].控制与决策，2003，18（6）：754-757.

[9]姜艳萍，樊治平.基于不同粒度语言判断矩阵的群决策方法[J].系统工程学报，2006，21（3）：249-253.

[10]Xu Y J，Wang H M.Approaches based on 2-tuple linguistic power aggregation operators for multiple attribute group decision making under linguistic environment[J].Applied Soft Computing，2011，11（5）：3988-3997.

[11]Wang J Q，Wang D D，Zhang H Y，et al.Multi-criteria group decision making method based on interval 2-tuple linguistic information and Choquet integral aggregation operators[J].Soft Computing，2015，19（2）：389-405.

[12]Merigo J M，Gil-Lafuente A M.Induced 2-tuple linguistic generalized aggregation operators and their application in decision-making[J].Information Sciences，2013，236（1）：1-16.

[13]刘金培，林盛，陈华友.二元语义Bonferroni集成算子及其在多属性群决策中的应用[J].运筹与管理，2013，22（5）：122-127.

[14]Zadeh L A.The concept of a linguistic variable and its application to approximate reasoning Part I[J].Information Sciences，1975，8（2）：99-249.

[15]Zhang H M.The multiattribute group decision making method based on aggregation operators with intervalvalued 2-tuple linguistic information[J].Mathematical and Computer Modelling，2012，56（1）：27-35.

[16]林建，兰继斌，林耀海.基于区间二元语义集结算子的多属性群决策方法[J].吉林师范大学学报，2009，30（1）：5-9.

[17]Yager R R.On generalized Bonferroni mean operators for multi-criteria aggregation[J].International Journal of Approximate Reasoning，2009，50（8）：1279-1286.

[18]Yager R R.On ordered weighted averaging aggregation operators in multicriteria decision making[J].IEEE Transactions on Systems，Man，and Cybernetics，1988，18（1）：183-190.