用户可自定义的低调整率保序加密算法

孙彦珺，杨 庚，史经启，刘国秀

SUN Yanjun,YANG Geng,SHI Jingqi,LIU Guoxiu

南京邮电大学 计算机学院、软件学院，南京 210003

School of Computer Science&Technology,School of Software,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

1 引言

随着云计算技术的不断发展，大量用户数据被上传并存储在云端数据库中。如何在有效利用这些数据的同时，保证用户隐私信息的安全，成为加密算法的研究热点之一。传统数据加密方案虽然可以有效降低存储在不可信服务器端机密信息的泄露，但由于无法直接对密文进行有效操作，因而需要先在客户端对密文解密后才能进行相关计算，浪费了云计算平台的计算能力。一种可行方案是将保序加密OPE（Order-Preserving Encryption）方案与云计算平台结合，允许用户在云端直接对密文进行特定计算。比较大小是数据库中常见的操作，如对某列数据进行比较、排序或范围查询等。OPE方案可以在提供较高安全保护级别的同时，为用户提供基于云端密文的有效计算服务。

2004年Agrawal等[1]提出了一种对数值型数据进行保序加密的方案（Order-Preserving Encryption Scheme，OPES），允许用户直接对密文进行比较操作，但该方案需要在已知明文的情况下预计分布，而且不能支持字符串等其他数据类型。2005年Li等[2]提出了前缀保留加密方案（PPE），能保证一定范围内的顺序信息，但不能严格地保证顺序大小，支持范围查询。2013年Popa等[3]提出的可变保序编码（mutable Order-Preserving Encoding，mOPE），可以支持任意数据类型的保序加密，但在数据进行插入删除操作时效率较低。

本文基于广义的平衡二叉搜索树（AVL-N树）提出了可变保序编码方案（general mutable Order-Preserving Encoding，gmOPE），支持任意数据类型的保序加密，允许用户自定义加密算法与调整策略，优化了二叉树重平衡调整与编码更新算法，提高了数据插入删除操作的效率。第2章对相关研究做出陈述；第3章描述mOPE方案的思路及缺陷；第4章提出改进后的gmOPE方案，并对其进行分析；第5章在理论上与现有方案对比分析gmOPE的算法性能和实用性；第6章实现两种方案，并基于不同量级的数据集对两者的性能测试对比分析；第7章对研究的内容进行总结。

2 相关研究

为方便衡量保序加密方案的安全性，Boldyreva等[4]介绍了一种新的OPE安全性标准IND-OCPA（indistinguishability under an Ordered Chosen Plaintext Attack），论证了如果仅假设一些具体的攻击环境，无法达到保序加密所需要的安全性。Liu发表的文献[5-6]，都利用加密函数Enc(v)=a×v+b+noise对明文v进行加密，通过添加噪声noise来提高其安全性。文献[6]针对索引加密数据提出了一种非线性保序方案，允许用户直接在密文数据库中进行范围查询。该方案不仅能够保存明文的顺序信息，还弥补了文献[5]中线性保序索引方案的安全漏洞。

2013年文献[7]提出可比较加密的概念，克服了保序加密的弱点，降低了加密数据公开的信息量，提高了CryptDB[8]和Monomi[9]的安全性。但该方案需要较大的密文长度，造成加密数据库的性能下降，减少了实用性。第二年，Furukawa[10]提出一种基于记号的可比较加密方法（token-based short comparable encryption），通过比较密文对应记号获得密文顺序信息，且密文长度较短。该方法对密文进行不等于判断时计算开销较大，但结合索引技术可以缩短延迟。

上述的保序加密方案主要都针对特定的数据类型加密，Popa等[3]提出的mOPE是一种密文可变的保序加密方案，可以支持任意数据类型的保序加密，且不会泄露除明文顺序以外的任何信息。该方案在插入明文前按顺序对应编码，之后用任意的确定加密算法加密明文，再把密文与对应编码存储在数据库中。因此mOPE是一种保序编码方案，而非保序加密方案。该方案利用二叉搜索树的性质对数据进行编码，再把加密后的数据与其对应编码同时存储在数据库中。当对密文进行比较操作时，在不解密的情况下，通过比较对应的保序编码获取密文顺序信息。然而因为需要保证二叉搜索树的平衡性，在数据库进行大量插入或删除操作时，会导致编码的频繁变更，给服务器带来很大的开销。

2015年，Boneh等[11]首次提出ORE方案（orderrevealing encryption），与OPE类似，直接通过密文获得明文顺序。该方案基于多重线性映射设计了第一个对密文进行大小比较的ORE系统，可以提供“最大可能”的语义安全。并且数据不局限于数值型数据，与Pandey等[12]PPE方案思想类似，更具通用性。之后，Chenette等[13]基于伪随机函数对优化了ORE方案，提升了效率和安全性。2016年，Lewi等[14]提出了一种新的ORE方案，具有比现有OPE和ORE方案更强的安全性，并且加密速度更快，能够有效抵御Naveed等[15]描述的推论攻击。文献[16]首先引入外包数据库的系统模型，指出隐藏数据分布和数据频率的重要性，并基于此提出了一种新的简单保序加密模型。

3 可变保序编码mOPE加密方法

3.1 mOPE简介

mOPE核心思想是利用平衡二叉搜索树的结构对密文数据进行编码。从根节点开始，记录每个节点的路径，并对二叉搜索树的每个节点进行二进制编码。密文数据存储在不可信的数据库中，当可信的客户端向其中插入新的数据时，通过一个交互方案，获得新数据的插入位置。如果新数据的插入破坏原平衡二叉树的平衡性，则需要重新调整新二叉搜索树，以保证平衡二叉搜索树的平衡性。

3.2 mOPE编码原理阐述

可变保序编码根据平衡二叉搜索树的节点路径进行编码，根据平衡二叉树的重平衡特性实现可变性。

将明文数据v插入数据库中逻辑平衡二叉树的具体步骤可以归纳成算法1，具体描述如下（Cl表示客户端Client，Ser表示服务器端Server）：

算法1遍历平衡二叉搜索树查找明文v的插入路径

输入：明文v

输出：路径path

（1）Cl↔ Ser：获取OPE_Tree根节点的密文 c′，此时path为空字符串。

（2）Cl：用户解密密文c′从而获得加密前的明文v′。

（3）Cl↔Ser：判断待插入明文v与明文v′的大小关系。若 v＜v′，则向左进行查找，path=path+“0”；若v=v′，则找到节点；若 v＞v′，则向右进行查找，path=path+“1”。

（4）Ser：服务器基于用户的反馈信息，返回下一个密文 c′，并执行步骤（2）。

（5）Cl&Ser：当找到v，或者服务器到达树的一个空节点时，算法终止，返回路径path。

如图1所示，数据库中存储了69、32、20、10、25加密后的密文、对应的编码信息。当插入新数据55时，按算法1的步骤操作，依次与32、69比较后得到插入位置的路径path为10。根据路径path进行二进制编码，先在 path后补“1”，然后补“0”直到达到规定长度OPE_LENGTH，即为该节点的二进制编码。例如，55的编码为[10]1。

通用编码公式定义如下：

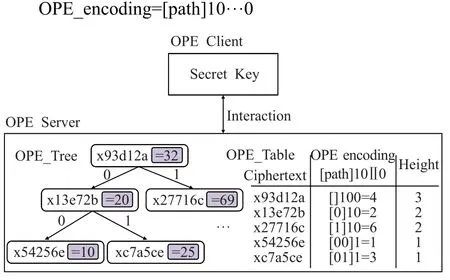
图1 mOPE数据结构概览

3.3 mOPE平衡调整策略

重平衡算法由Server端定义UDFs实现。用户在需要的时候向服务器发送UDFs请求，结合前文的交互实现重平衡。该算法具体描述如下：

算法2 mOPE重平衡算法

输入：节点的路径path

输出：无

（1）根据路径path，在OPE_Tree中从插入节点的父节点开始向根节点回溯。设当前回溯节点为p。

（2）查询数据库得到节点 p的高度h_root和左、右子树的高度h_left、h_right。由于插入新节点后，节点 p的高度可能会发生改变，记父节点新的高度h_root_new=max(h_left,h_right)+1。

（3）比较插入新节点前后节点 p的高度h_root和h_root_new，判断AVL树平衡性。如果高度不变，说明AVL树依然平衡，不需要重平衡，退出算法；否则，继续（4）。

（4）判断节点 p的左、右子树高度差值是否超过平衡因子，若超过则进行（5），执行“AVL旋转”操作；否则更新节点 p高度，继续往上回溯：节点 p指向当前节点父节点，转（2）。

（5）对以节点 p为根节点的子树进行“AVL旋转”，更新相关节点的OPE编码和高度Height，退出算法。

3.4 优缺点分析

mOPE可达IND-OCPA安全等级，是一种安全、高效的交互性保序加密方案。平衡二叉树是实现mOPE方案的关键数据结构，但是严格维护其平衡性会引发高频次的重平衡操作，严重降低算法效率，增加服务器计算开销，当数据库中存储大量数据时尤为明显。如果适当地放宽平衡二叉树约束条件，降低重平衡执行次数，可以在不对密文操作造成较大影响的情况下，显著降低服务器端的开销。

4 gmOPE编码方法

数据的插入操作主要分为两部分：定位数据插入位置并计算保序编码和保证逻辑二叉搜索树的平衡性。阶段1每次必须执行，阶段2则根据需要执行，且阶段2耗时较多，因此若能降低阶段2的执行频次，就能显著地提高数据插入的效率。本文通过放宽约束条件到N，将AVL扩展为广义平衡二叉树AVL-N，降低重平衡频次，提升算法效率。gmOPE基于广义平衡二叉树进行编码，使用“(N+2)+(N+3)”重构算法替换“AVL旋转”操作，因而比mOPE更具通用性。同时通过借助数据库临时表实现重排算法、设计正确且高效的编码更新规范等方法对算法进行优化，进一步提升算法整体效率。

4.1 平衡二叉树的重平衡方法

保证二叉树的平衡性，可以减少C/S交互次数，提高用户查询数据的效率。重平衡操作一般采用旋转法，但旋转调整的理论比较抽象，旋转方向又各不相同，代码量大且流程复杂，实际使用较为复杂。如果利用平衡二叉树“中为根、小为左、大为右”的特性来重组失衡子树，可以省去针对不同的失衡结构采用不同的旋转方法的复杂中间过程，使算法更为简单。

文献[17]提出了一种新的重平衡方法来替换“AVL旋转”操作，当平衡二叉树出现失衡，只需要从失衡节点开始，向深度较深的子树方向进行搜索，就可以得到失衡节点、一个较深子节点和较深子节点的较深子节点。把这三个主干节点和四个从属节点按照完全二叉树的结构进行重新排列，就可以恢复平衡。

本文在此基础上，扩展为“(N+2)+(N+3)”重构算法，并把该算法应用于广义的平衡二叉树中，该树允许用户自定义平衡因子N，又称为AVL-N树，并用此优化mOPE。扩展后的重平衡算法主要由两部分组成，算法3主要用于标识、保存2N+5个失衡节点，并利用算法4自动计算的失衡节点分类情况，把失衡树重构为完全二叉树，其中N+2个节点称为主干节点，主干节点对应二叉树OPE_Tree中单个节点；N+3个节点称为从属节点，从属节点对应OPE_Tree中的单个节点或某个子树抽象而成的抽象子节点。之后更新各个节点的编码和高度信息，以及N+3个抽象子节点下属所有节点的编码信息。算法4主要用于计算失衡节点对应的分类情况，求出重排后完全二叉树各节点相应的编号，并存储在数组index[]中。由于平衡二叉搜索树是通过编码OPE_encoding维护的逻辑二叉树，因此对于节点左、右孩子及父节点的查找，可以直接通过路径path定位到。该方法采用自动计算分类的形式，流程简单，易于操作。

当N=1时，AVL-N树的约束条件与普通的平衡二叉搜索树相同。如图2所示，图中数字为节点编号，四幅图中每幅图的左侧为失衡二叉树，右侧为重排后的结果。下面以第一类（对应左旋）为例详细讲解重排过程。

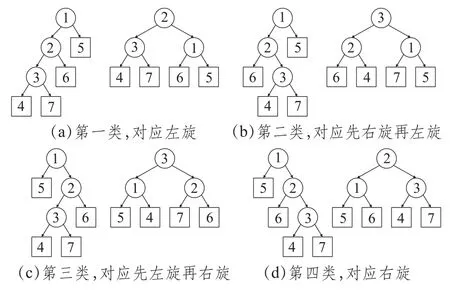
图2 四类重平衡情况示例

算法3 gmOPE重平衡算法-Rebalance

输入：失衡节点的路径path

输出：无

（1）查找并保存失衡二叉树的2N+5个节点信息。

①将失衡节点作为根节点，存入node[i](i=1)；

② 比较path+“0”节点和path+“1”节点的高度，高度较大的节点作为主干节点，较小的作为从属节点。主干节点存入node[i+1]，从属节点存入node[i+N+3]。i=i+1，若i＞N+1，转④，否则转③；

③将主干节点作为新根节点，并根据主干节点相对父节点的左右方向在path后补“0”或“1”，转②；

④node[N+3]=新根节点的左孩子，node[2N+5]=新根节点的右孩子。

（2）构建重排序完全二叉树：根据失衡二叉树和对应的有序完全二叉树构建重排序完全二叉树，得到广度优先遍历重排序完全二叉树节点数组index[]。

index[]=（算法 4）

（3）将失衡二叉树按照重排序完全二叉树重构，更新节点编码，详见3.3节。

更新高度：由叶子节点开始向上，根据左右子节点高度计算并更新父节点高度h_root_new=max(h_left,h_right)+1，并向上回溯至重排序完全二叉树根节点。

注：有序完全二叉树是指按照广度优先遍历方式遍历二叉树，得到的是有序数列。下文概念相同。

建立一个大小为8的节点指针数组node[8]收集并保存节点信息：0号节点为失衡节点的父节点，1号节点为失衡节点，2号节点为1号节点较深的子节点，5号节点为1号节点较浅的子节点。以此类推，直到所有失衡二叉树节点都收集完成，采集到的节点数组为图2中第一类对应的编号。失衡节点的父节点可以通过路径path去掉最后一位后往上回溯求得，与node[0]效果相同，因此文章不单独列出node[0]，默认为节点node[1]～node[2N+5]。之后根据算法4，求出重排后完全二叉树各节点相应的编号，生成重平衡后的广度优先遍历数组index[]=[2，3，1，4，7，6，5]（详细步骤见4.2节）。最终根据index[]数组即可重建平衡二叉搜索树，并根据算法3更新AVL树对应数据项的编码和高度，至此完成了一次重平衡操作。

4.2 构建重排序二叉树及改进

当N=1时重排后的完全二叉树有4种类型，每种类型对应的数组中包含7个编号元素；当N=2时有8种类型，包含9个编号元素。以此类推，N越大对应的分类情况越多，计算量也越大，人工难以胜任。因此结合算法4，采用自动计算分类的形式，可以直接计算出失衡树对应的重排数组，简化计算过程。算法4的主要功能是根据采集到的失衡树节点，求出重排后的节点编号，构建完全平衡二叉树。具体算法内容如下：

算法4

输入：平衡约束N，收集的节点数组node[]

输出：重排序完全二叉树节点数组index[]

（1）中序遍历（LDR）失衡树，得到对应的编号数组UBTArray[]。

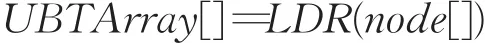
（2）构建包含2N+5个节点的有序的完全平衡二叉树，中序遍历完全二叉树，得到完全二叉树数组CBTArray[]。

（3）根据上面的两个数组，构建重排序完全二叉树，得到对应的广度优先遍历数组index[]。

算法4由三部分组成，以第一类情况为例，说明重排过程。如图3所示，中序遍历失衡树得到数组UBTArray[]=[4，3，7，2，6，1，5]，然后构建包含 2N+5个节点的有序完全二叉树并进行中序遍历，记为数组CBTArray[]=[4，2，5，1，6，3，7]。步骤（3）结合UBTArray[]和CBTArray[]，得到重排后的索引数组index[]=[2，3，1，4，7，6，5]，即为重排完全二叉树的广度优先遍历结果。结合路径path和编码OPE_encoding，在算法3中即可完成重平衡操作。

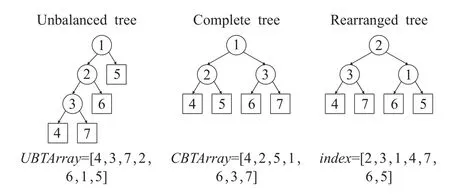
图3 算法4讲解图例

算法4主要涉及数组操作和中序遍历操作，在高级编程语言中实现较为简单。由于算法4不涉及任何客户端操作，同时为省去不必要的通信开销，将算法4定义成数据库UDF，借助数据库临时表实现重排算法。通过临时表实现重排算法，使逻辑更加直观简洁，省去了构建完全二叉树和中序遍历等操作，既简化了算法步骤，又节省了计算时间，提升了算法效率。以图2第一类情况说明UDF具体实现过程。

首先将节点node编号按采集顺序依次存入临时表（图4（a））。OPE_LENGTH取值为4，将OPE_encoding的值与节点编号对应存入表中。再将表格内容按照OPE_encoding编码大小排序，达到与中序遍历相同的效果，node编号排序随之改变。然后将中序遍历有序完全二叉树的结果数组CBTArray[]存入列CBT编号，如图4（b）所示。最后将图4（b）对列CBT编号执行order by语句，即可得到图4（c）中的结果，此时node编号列的内容即为重排后的完全二叉树广度优先遍历的结果。之后按算法3的后续步骤即可完成一次重排序过程。改进后的算法4借助数据库临时表，通过order by语句达到中序遍历相同的效果，简化了重新生成index[]数组的过程。

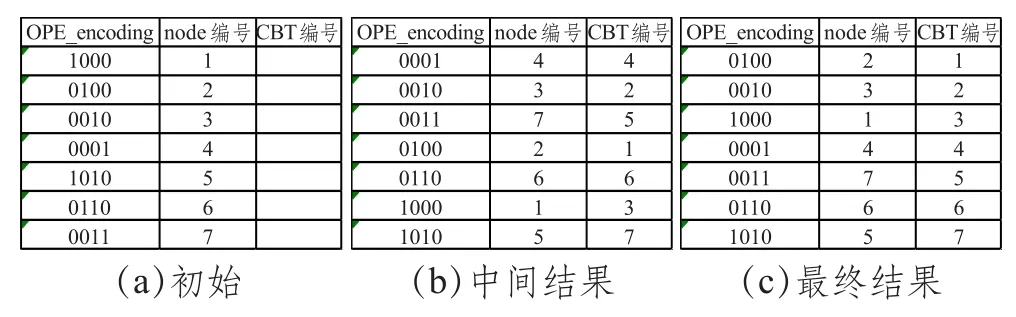
图4 数据库临时表实现重排算法

4.3 更新从属节点及子节点编码

当在执行算法3的步骤（2）生成了重排序完全二叉树之后，需要更新2N+5个失衡节点对应的编码和高度信息。对于重平衡后树中节点的高度，根据调整后的二叉树结构，自底向上依次对各个节点进行更新即可；而对于节点编码，则要设计一种高效、正确的编码更新规范。

由于节点路径path发生变化，节点编码OPE_encoding也随之改变，并且改变前后的节点编码均只与路径path有关。将所有节点编码拆分为前缀prefix和后缀suffix，前缀prefix由路径path决定，后缀suffix由各节点在子树内部的具体路径决定。定义编码调整公式为：

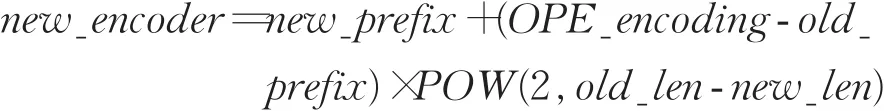
其中new_len和old_len分别为新旧路径的长度。

对整张表进行编码更新会明显降低执行效率，尤其是在数据库中已经存在大量数据记录时。因此可以结合叶子节点对应的编码范围[min，max]限定受影响的节点，从而在正确更新编码的同时，保证编码更新效率。

5 理论分析

5.1 gmOPE时间复杂度分析

本文介绍的mOPE方案和新提出的gmOPE方案，插入过程都主要分为两个阶段：阶段1包括定位插入位置、计算OPE编码、改写SQL语句和向数据库中插入密文记录；阶段2为检查逻辑二叉树是否失衡并触发重平衡算法。

在第一阶段，逻辑平衡二叉树相关操作的时间复杂度最大。客户端与服务器交互，找到待插入数据的位置。假设数据表中已经存在n个数据项，由于两种方案的实现方式均为平衡二叉树，因此具有相似的时间复杂度。客户端与服务器在最好情况下需要进行(lbn」+1)次通信交互，以及相应次数的加解密操作；而在最坏情况下，mOPE仍然为(lbn」+1)，gmOPE由于平衡因子由1扩展到了N，因此需要多进行N次交互操作，复杂度为 (lbn」+1)+N 。

在第二阶段，所有操作均在服务器端进行，因此没有通信开销，仅有平衡性检测和重平衡开销。两种方案在每次插入数据后都调用UDF函数检查平衡性，当存在失衡节点时，可能会不断回溯至根节点，即为最坏情况O(lbn)；当二叉树仍然平衡时，结束回溯操作，即为最好情况O(1)。gmOPE判断失衡的方法与AVL方案一致，因此两者时间复杂度相似。重平衡操作时，在最好情况下，gmOPE需要平衡包含空节点在内的2N+5个节点，mOPE要平衡7个节点；最坏情况即为调整整个树，两者时间复杂度均为O(n)。

mOPE方法基于普通平衡二叉树来编码，大约每插入两次数据就会触发一次重平衡操作。而gmOPE基于广义平衡二叉树AVL-N来编码，降低了插入数据时触发重平衡操作的概率，N越大，触发重平衡操作的概率就越低。假设插入相同的数据量为n，gmOPE重平衡操作的次数n2小于mOPE的n1，因此gmOPE的重平衡频率 fg也小于mOPE的 fm，即 fg≤fm（ N=1时等号成立）。又因为单次时间复杂度基本相同，所以gmOPE重平衡操作的平均时间复杂度更具优势。重平衡操作在整个插入过程中耗时最多，因而虽然单次插入操作时由于N的存在gmOPE时间复杂度略微高于mOPE，但多次插入时，由于gmOPE调整频次比mOPE低得多，因此gmOPE整体时间复杂度更具优势。

在实际生产环境中，数据库的记录数n≫N，因此N可以忽略不计，O(N)即为O(1)，见表1。

表1 mOPE与gmOPE时间复杂度比较

5.2 gmOPE实用性对比

2015年，Boneh等[11]首次提出了一种基于多重线性映射的保序加密概念ORE。该方案虽然为最新研究成果，为保序加密提供了新的研究思路，但在安全性方面仍有不足，且在应用实现上有一定难度，而mOPE已经在CryptDB[8]系统中得到实际应用。本文在mOPE基础上改进提出的gmOPE方案，可以自定义UDFs函数配合现有数据库使用，不需要对数据库做定制，并能根据需要结合现有加密方案增强安全性，安全性达到INDOCPA等级，更好地应用于实际生产环境。因此与ORE和mOPE相比，gmOPE兼顾了安全性与效率，可以在实际应用中发挥其优势，见表2。

6 实验数据与分析

本文分别实现了mOPE和gmOPE，并且在相同的实验环境中对两种方案分别进行了测试。mOPE和gmOPE程序均为C/S结构，分为客户端和服务器端两部分。客户端使用Java实现，通过JDBC与服务器通信；Server端主要为MySQL数据库。Server端数据库为未经修改的普通MySQL数据库，包含用户事先实现的自定义UDFs，用来实现逻辑二叉树调整及编码调整策略。客户端程序主要功能为定位插入位置、数据加解密等计算操作，Server端主要负责编码的调整和逻辑二叉树的维护。其中加解密算法为电子密码本模式的分组AES加密算法，分组长度为128位。

6.1 实验平台

硬件平台主要为服务器节点。Server节点运行数据库及UDFs函数，配置为：CPU为Intel®Xeon E3-1225 v3，3.2 GHz/8 MB缓存；内存为16 GB（2×8 GB）1 333 MHz Dual Ranked RDIM；硬盘为1 TB 3.5-inch 7.2 K RPM SATA II Hard Drive。软件平台：操作系统为：Centos 6.6，数据库为mysql-5.1.73，JDK版本为64位1.7.0_45。

实验中将客户端放置在服务器节点一同运行程序，忽略客户端和Server端的通信时延，主要对数据插入操作的性能进行分析对比。

数据集：mOPE和gmOPE采用同一数据集，为使用Python随机生成的包含5 000条不重复的整数型数据的数据集Data{r1，r2，…，r5 000}，满足对任意 i,j，ri≠rj，ri与rj的大小关系随机。

6.2 实验结果分析

分别对mOPE和gmOPE中AVL-N 树 N 为1、2、3、4、5五种情况下的方案进行测试，比较它们的性能差别，分析在不同情况下插入不同数据量的明文数据所需的时间以及触发重平衡操作的次数。

6.2.1 调整时间

图5为两个阶段总的时间消耗随插入数据量的变化，包括阶段1中的计算时间和数据库插入耗时，阶段2中调用UDF函数检查二叉树平衡性并重新调整二叉树和编码。其中阶段1的计算量主要由查找明文插入位置、加解密操作、重写SQL语句和数据库插入操作组成，mOPE和gmOPE的每一次插入操作均必须经过阶段1的所有步骤，因此两种方案在阶段1的耗时基本相同。且gmOPE方案中N的增大并未对阶段1的耗时造成明显影响。图6为阶段1的耗时随插入数据量的变化。在插入5 000条数据的时候，mOPE和gmOPE在N取不同值时阶段1耗时均约为139 s，其中计算时间约为15 s，插入耗时约为124 s。

表2 OPE/ORE方案对比分析

阶段1的操作为mOPE和gmOPE的共同部分，时间消耗基本一致，两者时间开销的差别主要集中在阶段2的二叉树重平衡操作部分，因此下面重点分析两者在阶段2的时间差别，对比分析两者的性能。

图7为阶段2的耗时随插入数据量的变化，观察可知两个方案均具有稳定性，调整时间随数据量的增加稳定增长，没有出现因为数据量的增加而导致操作时间急剧增长的情况。gmOPE在N=1的时候即为普通的AVL树，与mOPE效果一样：两者触发重平衡操作的频次如图8所示，完全一致；由于gmOPE具有通用性，在收集失衡节点及二叉树调整等操作步骤的时候比AVL复杂，因此调整操作比mOPE耗时多，实验显示插入5 000条数据，gmOPE（1）阶段 2耗时比 mOPE多出24.6%。但随着N的增大，gmOPE在插入数据过程中触发重平衡操作的次数显著下降，重平衡操作的总耗时也随之下降。虽然单次二叉树调整操作gmOPE耗时比mOPE多，但因为gmOPE调整频次显著下降，因而gmOPE在N≥2时的整体效率优于mOPE。结果显示，在N=2～5时，gmOPE在阶段2中调整操作的耗时比mOPE节省约2.8%～34.8%。当N取值为5时，gmOPE阶段2效率比mOPE提升约53.3%，整体效率提升约40.4%。并且随着N的继续增大，gmOPE效率提升会更加显著。

6.2.2 调整频次

图8描述的是两种方案在插入不同数据量的数据时所触发的重平衡操作的次数，gmOPE在N=1时AVL-N即为普通的AVL树，调整次数与mOPE完全一致。随着N的增大，gmOPE的重平衡次数具有越来越明显的优势：当 N=2时，gmOPE的调整次数仅为mOPE的50.7%；N=3时，gmOPE的调整次数已经下降为mOPE的22.2%。

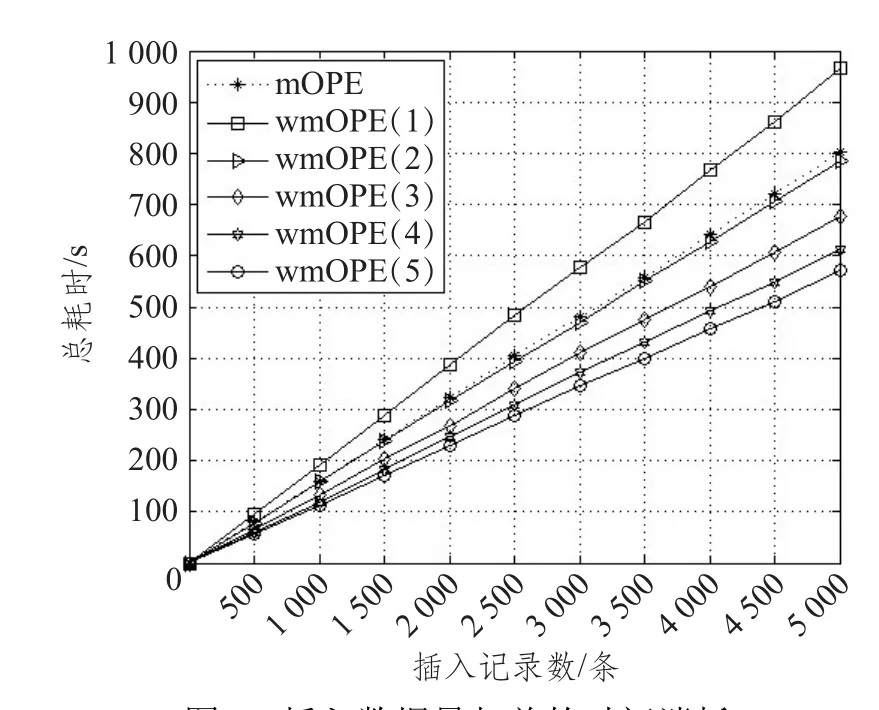
图5 插入数据量与总的时间消耗

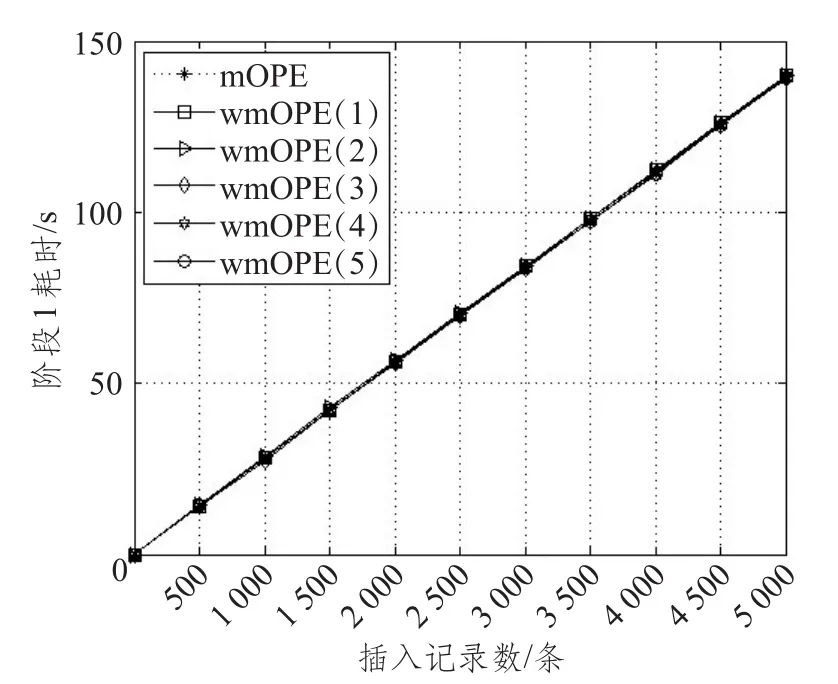
图6 插入数据量与阶段1的耗时

图7 插入数据量与阶段2的耗时

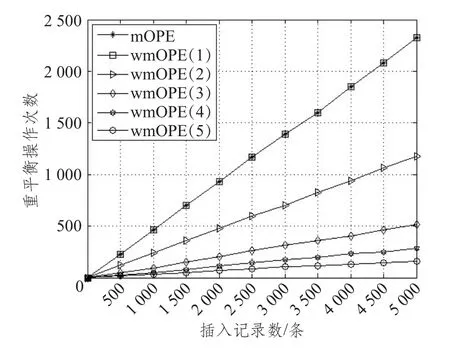
图8 插入数据量和触发重平衡操作的次数

图9是当用户向数据库中插入5 000条数据时，触发重平衡操作的次数随广义平衡二叉树中N的大小的变化关系。从图中可以看出，在gmOPE方案中，随平衡因子N的增大，触发重平衡的操作次数有显著的降低。当N=11时，插入同样的数据量，gmOPE的重平衡次数只有mOPE的千分之一。

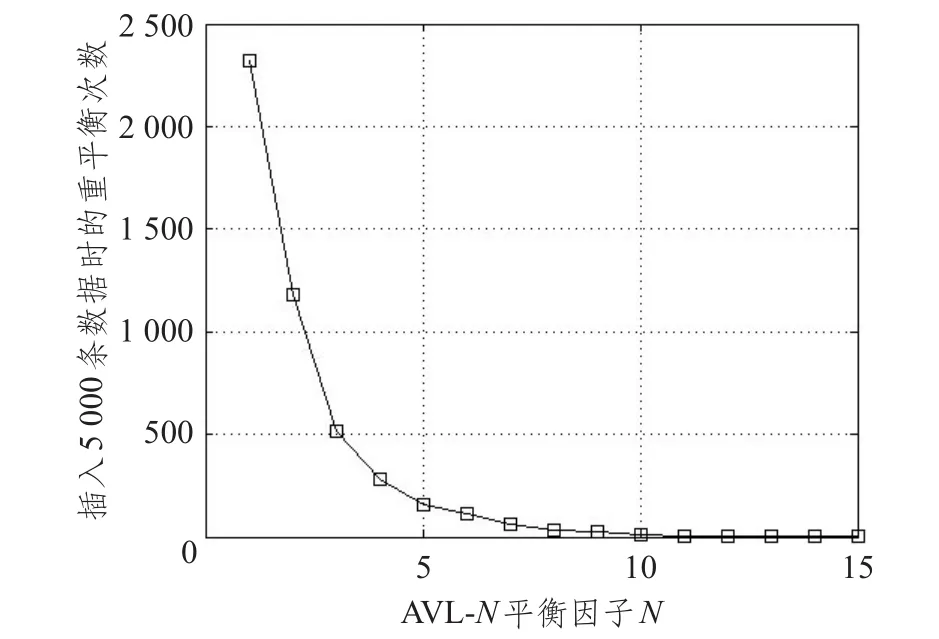
图9 平衡因子N与插入数据时触发重平衡操作的次数

7 小结

本文利用广义的平衡二叉搜索树，实现了可变保序编码方案gmOPE，并取得了较为理想的实验结果。把该保序加密方案运用在数据加密系统中，可以让客户端能直接对密文数据库中的数据进行检索等操作，且支持任意类型数据的保序加密。gmOPE加密方案允许用户自定义平衡约束条件，采用新型的重平衡调整方法，既保证了保序加密方案的可变性，又减少了重平衡的次数，提高了效率。实验结果表明，gmOPE整体效率得到大幅提升，在N=5时，整体效率提升约40.4%。

参考文献：

[1]Agrawal R，Kiernan J，Srikant R，et al.Order preserving encryption for numeric data[C]//Proceedings of the 2004 ACM SIGMOD International Conference on Management of Data，2004：563-574.

[2]Li J，Omiecinski E R.Efficiency and security trade-off in supporting range queries on encrypted databases[C]//IFIP Annual Conference on Data and Applications Security and Privacy，2005：69-83.

[3]Popa R A，Li F H，Zeldovich N.An ideal-security protocol for order-preserving encoding[C]//2013 IEEE Symposium on Security and Privacy，2013：463-477.

[4]Boldyreva A，Chenette N，Lee Y，et al.Order-preserving symmetric encryption[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques，2009：224-241.

[5]Liu D，Wang S.Programmable order-preserving secure index for encrypted database query[C]//2012 IEEE Fifth International Conference on Cloud Computing，2012：502-509.

[6]Liu D，Wang S.Nonlinear order preserving index for encrypted database query in service cloud environments[J].Concurrency and Computation：Practice and Experience，2013，25（13）：1967-1984.

[7]Furukawa J.Request-based comparable encryption[C]//European Symposium on Research in Computer Security，2013：129-146.

[8]Popa R A，Redfield C，Zeldovich N，et al.CryptDB：Protecting confidentiality with encrypted query processing[C]//Proceedings of the Twenty-Third ACM Symposium on Operating Systems Principles，2011：85-100.

[9]Tu S，Kaashoek M F，Madden S，et al.Processing analytical queries over encrypted data[J].Proceedings of VLDB Endowment，2013，6（5）：289-300.

[10]Furukawa J.Short comparable encryption[C]//International Conference on Cryptology and Network Security，2014：337-352.

[11]Boneh D，Lewi K，Raykova M，et al.Semantically secure order-revealing encryption：Multi-input functional encryption without obfuscation[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques，2015：563-594.

[12]Pandey O，Rouselakis Y.Property preserving symmetric encryption[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques，2012：375-391.

[13]Chenette N，Lewi K，Weis S A，et al.Practical orderrevealing encryption with limited leakage[C]//Proceedings of the 23rd International Conference on Fast Software Encryption（IACR-FSE），2016：474-493.

[14]Lewi K，Wu D J.Order-revealing encryption：New constructions，applications，and lower bounds[C]//Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security，2016：1167-1178.

[15]Naveed M，Kamara S，Wright C V.Inference attacks on property-preserving encrypted databases[C]//Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security，2015：644-655.

[16]Liu Z，Chen X，Yang J，et al.New order preserving encryption model for outsourced databases in cloud environments[J].Journal of Network and Computer Applications，2016，59：198-207.

[17]江顺亮，胡世鸿，唐祎玲，等.低调整率的广义AVL树及其统一重平衡方法[J].计算机应用，2015，35（3）：654-658.