考虑轮胎模型的割草机车架瞬态强度分析

张云鹤 杨 为

（重庆大学机械传动国家重点实验室 重庆 400044）

引言

割草机的车架类似于全地形车的车架。国内割草机产量大，主要用于出口。但国产割草机多数是对国外类似车型的简单模仿，属于低端产品，技术含量较低，安全性有待验证。目前，余烽等人[1]对全地形车进行了整车振动舒适性仿真分析，建立了全地形车多体动力学模型，用来预测全地形车整车振动舒适性；张志飞等人[2-3]建立了用于进行稳定性分析的全地形车整车多体动力学模型；贺岩松等人[4]对全地形车设计的人机功效进行了校核。总结已有的研究工作可知，国内关于全地形割草机研究的文献中，很少有对割草机冲击过程进行瞬态动力学分析的研究。

在实际工作过程中，割草机受到来自路面的随机激励以及发动机对整车的激励，割草机总成和各个部件所受到的载荷是随工况变化而变化的动载荷[5]。对割草机进行瞬态动力学分析，可了解割草机车架在动载荷作用下，其各部位瞬态应力随时间的变化关系，结合材料性能，验证割草机车架设计的准确程度，为割草机结构的优化设计提供依据。同时，有助于对割草机整车设计的不足有更清楚的认识，为提高割草机在使用时的安全性奠定良好的基础[6]。

1 考虑轮胎模型的割草机车架有限元模型

轮胎是车辆的重要组成部件,它不仅支承负荷，向地面传递动力,而且承担缓冲减震等作用。同时，它对车辆的乘坐舒适性、操纵性、安全性、经济性、效率等方面均产生重要影响。

1.1 轮胎模型的建立

模拟轮胎接触响应的动力学方程如公式（1）所示。

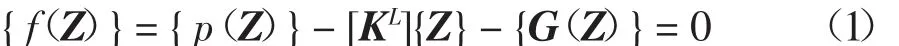
式中：{Z}为响应变量向量；{p（Z）}为外载荷向量；[KL]为线性系统矩阵；{G（Z）}为非线性项向量。

利用增量Newton-Raphson法求得公式（1）的解，求解以下i次迭代的线性方程组。

由于响应变量的不精确值{Z}i和[K（Z）]i被认为是非线性方程的雅可比矩阵，其mn分量（第m行、第n列分量）定义为：

继续进行公式（2）和公式（4）所描述的迭代过程，直至达到收敛或达到规定的最大迭代次数为止[7]。

1.1.1 轮胎网格划分方法

由于轮胎的截面结构包含将近20种不同的材料，且每种材料形状各异，交错复杂，目前通用的有限元网格生成软件大都无法对轮胎截面的网格进行划分。即使采用通用的有限元网格生成软件对网格进行划分，由于各种束缚，也很难得到理想的单元形状，且同样需要很多的前期几何处理。对轮胎网格的自动划分是不可行的，所以在轮胎行业中，轮胎截面的网格一般采用人工划分。

由于轮胎截面关于整个轮胎是轴对称的，将轮胎截面绕轮胎轴线旋转360°后即可形成三维轮胎模型。故首先对二维轮胎截面结构图进行网格划分，然后旋转360°，形成完整的三维轮胎有限元模型。

1.1.2 轮胎网格划分原则

划分轮胎网格时，要综合考虑网格数量、网格疏密程度、网格质量以及节点单元编号。本着用尽可能少的单元数来尽可能准确地模拟复杂轮胎几何形状和材料分布特征，轮胎网格的划分原则如下:

1）对轮胎几何形状进行少量的简化，忽略胎冠花纹、胎侧防擦线、标志线等细节部分；

2）由于轮胎各部分材料的力学性能存在差异，故严格按照材料分界线进行单元划分；

3）只在材料分界尖角处使用有限元计算精度较差的三角单元，其他地方均使用四边形单元。

4）网格尺寸要适当控制。在应力集中处，如胎圈部位和带束层端部等应力应变梯度较大的区域，单元要适当细化。

由于轮胎截面结构图是一个左右对称的图形，因此可先对轮胎截面结构图的左半面进行处理，得到左半面的节点，然后利用镜像得到右半面的节点，进而得到整个轮胎截面有限元模型的节点。轮胎截面网格划分步骤流程图如图1所示[8]。

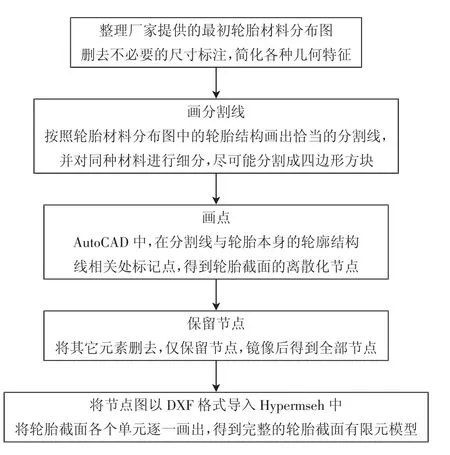
图1 轮胎截面网格划分步骤流程图

1.2 车架模型的建立

割草机的车架主要由薄壁的方钢和圆形钢管构成。由于车架是由薄壁件焊接而成的，利用4节点的壳单元来模拟，可以得到比梁单元更高的精度。连接部位的焊接一部分用共节点的形式模拟，一部分利用rigid单元进行模拟。其中，悬架减震单元用1D弹簧单元进行模拟，悬架的各零部件之间采用revolute单元进行连接。割草机车架的有限元模型如图2所示，包含227 584个节点、213 568个单元。其中包括174 269个壳单元、2个弹簧单元、24个beam单元、7个集中质量单元、39 116个实体单元、28个旋转铰接单元等。车架的材料为Q235，其材料属性为：弹性模量E=2.06×105MPa。泊松比为0.29，屈服极限[σy]=235MPa，断裂极限[σs]=375~460MPa。

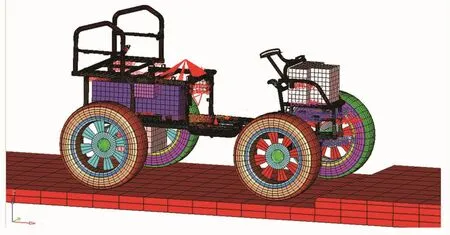
图2 割草机车架的有限元模型

2 瞬态动力学分析

2.1 瞬态动力学平衡方程

在有限元分析程序中，所有的动力分析类型都是基于下述有限元系统的通用运动方程式：

式中：M为质量矩阵；C为阻尼矩阵，研究中，采用比例阻尼计算方法求解 C，即，C=α0M+α1K，系数α0，α1可由实验方法或经验确定；K为刚度矩阵；U¨为节点加速度向量；U˙为节点速度向量；U为节点位移向量；F（t）为随时间变化的载荷向量。

在任意给定的时间t，方程式（5）可认为是一系列静态的方程式，是表征离散时间点的公式，它同时考虑了惯性力MU¨和阻尼力CU˙。用显示中心差分法求解方程式（5），相邻时间点之间的时间增值称为积分时间步长[9]，用Δt表示。

2.2 显示中心差分法

假定 0，t1，t2，…，tn时刻的节点位移、速度与加速度均已知，求解tn+1（t+Δt）时刻的结构响应。中心差分法对加速度、速度的导数采用中心差分代替，即：

求解线性方程组（7），可获得（t+Δt）时刻的节点位移向量 Ut+Δt，将 Ut+Δt代入几何方程与物理方程中，可获得（t+Δt）时刻的单元应力与单元应变。

由上述计算可知，用中心差分法求解（t+Δt）时刻的位移向量 Ut+Δt时，只需根据（t+ Δt）时刻以前的变量计算出Mˆ与Rˆ，即可计算出 Ut+Δt。

时间步长Δt的选择涉及2个方面的约束：

1）在直接积分法中，实质是用差分代替微分，且对位移和加速度的变化采用引申的线性关系（外插），这就限制了Δt的取值不能过大，否则结果可能失真过大，不能正确表现冲击振动的真实响应；

2）数值稳定性问题。在每一步数值计算中，不可避免地存在舍入误差，这些舍入误差又不可避免地代入下一个时间步的计算式中。如果算法不具备数值稳定性，可能导致结果发散，不能正常表现真实响应，甚至无法求解。

计算误差的控制要求Δt的取值不能过大，这取决于算法本身对误差的容限。

中心差分算法的稳定条件是时间步长必须小于由该问题的求解方程性质所决定的一个时间步长临界值。时间步长临界值的计算公式为：

式中：Tn为有限元系统的最小固有振动周期，s。一般只需求解系统中最小尺寸单元的最小固有振动周期min（）即可。

计算中，考虑到时间步长Δt的2种约束及中心差分法的稳定条件，采用“变时间步长法”，即每一时刻的时间步长Δt由当前结构的稳定性条件控制。具体算法为：计算每一个单元的极限步长Δtei，i=1，2，…，取 Δt=min（Δte）i为下一时刻的时间步长。各种单元的Δtei的计算方法如下：

1）杆单元、梁单元

式中：α为时步因子，系统默认0.9；L为杆单元与梁单元的长度，mm；c为杆单元与梁单元材料的声速，mm/s。c的计算公式为：

式中：Lmin为板单元的最小单元边长度，mm；c为板单元材料的声速，mm/s。c的计算公式为：

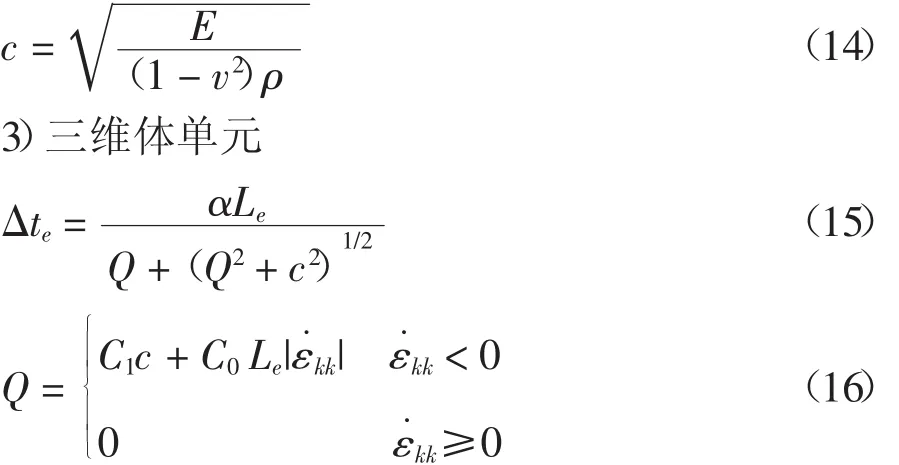
式中：Ve为单元体积，mm3；Aemax为单元最大一侧的面积，mm2。c为三维体单元材料的声速，mm/s。C0和C1为无量纲常数，默认值分别为1.5和0.06。c的计算公式为：

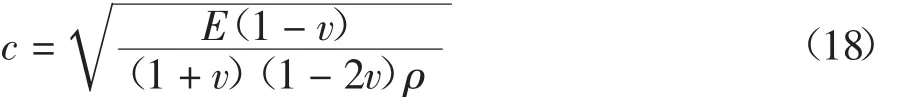
用中心差分法求解方程式（5）的步骤如流程图3所示。

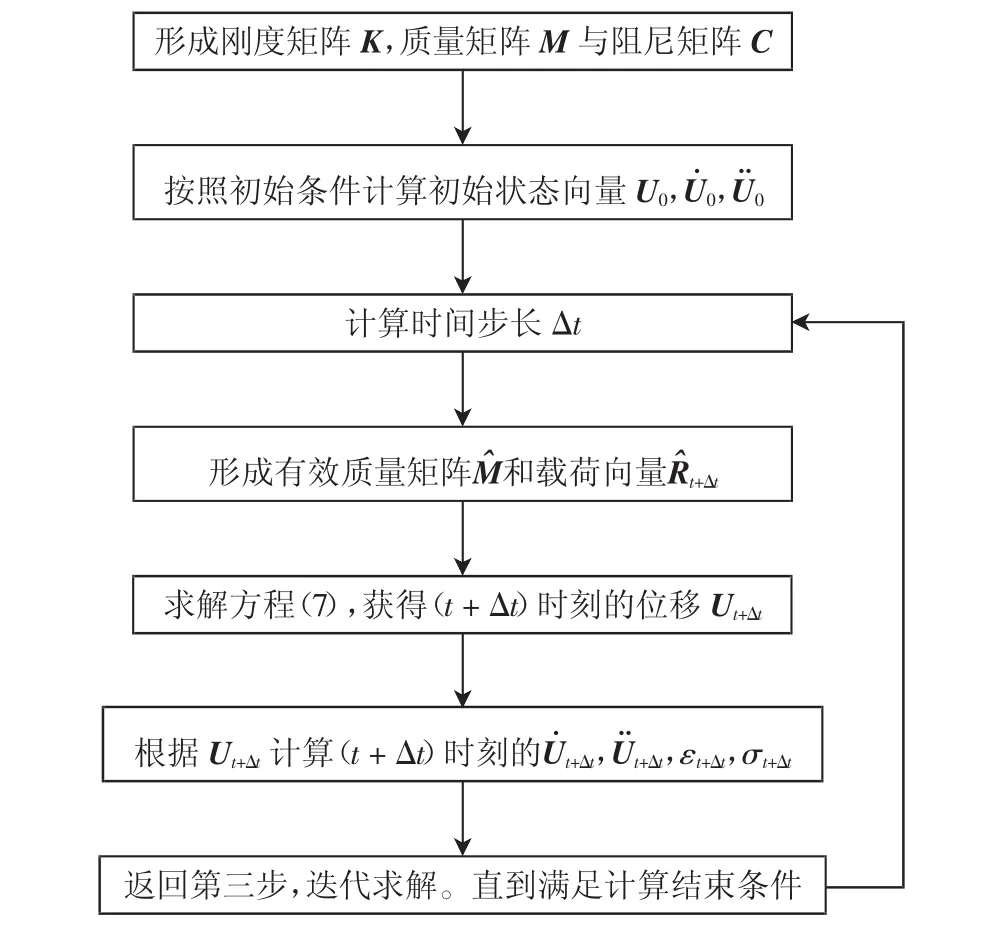
图3 中心差分法求解步骤流程图

3 结果和讨论

为了分析割草机车架在通过100mm高的台阶时的瞬态应力分布情况，采用LS-DYNA求解器对割草机整车进行瞬态动力学分析。

1）确定割草机的载荷条件。割草机的载荷主要由车架承担，割草机的参数参见表1，满载时整车质量为500 kg。油箱、发电机组、电瓶及后桥加驱动电机均采用六面体实体网格进行模拟。

表1 割草机车架瞬态分析的载荷条件

2）根据实际安装情况，利用1D单元将实体单元连接到割草机的车架上。

3.1 连接板处单元的时间历程曲线

通过对仿真过程中连接板处单元的时间历程曲线进行观察，将对车辆在不同时刻的工作状态有一定认识。提取图4中红圈内车架下纵梁与立柱的连接板处的595823号单元时间历程曲线，如图5所示。

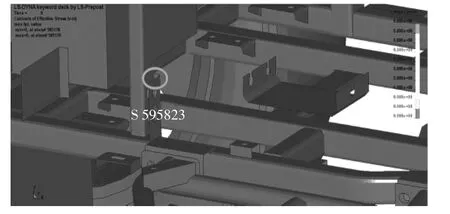
图4 车架下纵梁与立柱的连接板局部放大图

从图5可知，在前0.5 s，车架在重力加速度的作用下逐渐达到稳态。考虑到整体计算时间的限制，整个分析过程并没有等整车系统达到稳态后再增加车速，而是在0.5s就开始对整车赋予2m/s的行进速度。图5中，B点峰值阶段为割草机前轮通过台阶的时间段，C点峰值阶段为割草机后轮通过台阶的时间段。

3.2 危险应力区域

在割草机前轮通过台阶的过程中，最大应力区域出现在车架与前立柱的连接位置，出现时间在0.785 s，最大应力为213MPa，如图6所示。局部放大图如图7所示。

在割草机后轮通过台阶的过程中，最大应力区域出现在车架与后立柱的连接位置，出现时间在2.2 s，最大应力为204MPa，如图8所示。局部放大图如图9所示。

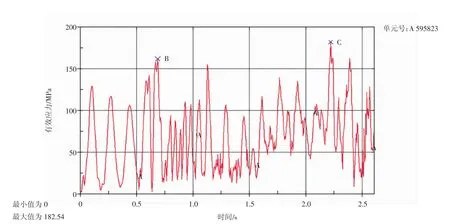
图5 595823号单元的时间历程曲线

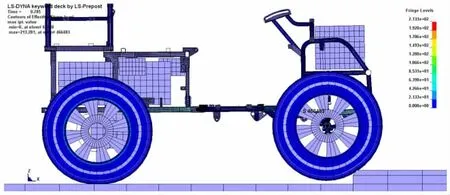
图6 割草机前轮通过台阶图

图7 车架与前立柱的连接位置局部放大图

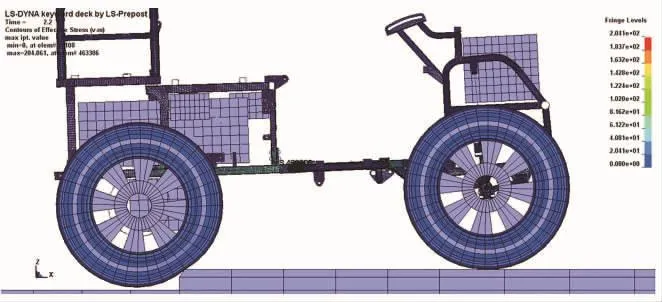
图8 割草机后轮通过台阶图

图9 车架与后立柱的连接位置局部放大图

4 结论

从割草机车架的瞬态动力学分析结果可得出如下结论：

1）割草机在通过一定高度的台阶测试中，车架危险位置的最大应力处于车架所用材料的屈服极限以内，割草机整车的强度符合要求。

2）由于动载荷作用，车架在越过台阶的过程中，危险位置的应力出现2次较大的峰值，对割草机结构的安全性存在一定隐患。

3）应重点关注这2个危险区域，加大连接板的厚度，或者在结构上进行相关优化。

1 余烽，徐中明，张志飞.基于ADAMS的全地形车整车振动舒适性仿真分析[J].机械设计与研究，2015（2）：160-163

2 张志飞，徐中明，彭旭阳，等.全地形车操纵稳定性建模与仿真[J].重庆大学学报：自然科学版，2009，32（6）：620-624

3 赵伟，张志飞，彭旭阳，等.ATV车体动特性分析[C]//朱位秋.第九届全国振动理论及应用学术会议论文集.杭州：浙江大学出版社，2007：200-206

4 贺岩松，李耀光，徐中明，等.全地形车集成设计人机工效校核与分析[J].人类工效学，2012，18（3）：54-57

5 姚宾，王艺颖，孟斌.客车车身骨架的瞬态动力学分析[J].汽车零部件，2014（12）：35-38

6 谢志强，杨建国.柴油机机体瞬态动力学的有限元分析[J].武汉理工大学学报（交通科学与工程版），2007，31（3）：521-524

7 Danielson K T,Noor A K,Green JS.Computational strategies for tiremodelingand analysis[J].Computers&Structures,1996,61(4):673-693

8 胡坚皓.载重子午线轮胎的网格划分及有限元分析[D].上海：东华大学，2011

9 白金泽.LS-DYNA3D理论基础与实例分析[M].北京：科学出版社，2005