航天器大型网状天线透光性遮挡的精确计算方法

杨 炀，张东来，柳新军，李安寿

(1. 哈尔滨工业大学深圳研究生院，深圳 518055；2.深圳航天科技创新研究院，深圳 518057)

0 引 言

对大部分航天器，太阳电池阵是唯一能源提供器。太阳电池阵由多个太阳电池片串联形成电池串，再将多个电池串并联组成。由于电池串输出电流受制于其中输出最小的电池片，当单片太阳电池被完全遮挡时，尽管在每一片(或数片)电池片上并联旁路二极管可避免遮挡时串联组件输出电流的减少，但仍会造成组件输出电压下降。为提高效费比，通常把太阳电池阵的最大功率点电压设计为略高于母线电压，在目前常用的S3R、S4R拓扑中，由于不具备最大功率点跟踪能力，受遮挡后一旦最大功率点电压下降至母线电压以下，就会造成显著输出功率损失[1-2]。因此，设计航天器时应尽量避免太阳电池阵受到遮挡。但在通讯卫星、多舱空间实验室这些具有大型结构的航天器上，很难保证太阳电池阵一直不受部分遮挡。因此，需要对遮挡情况进行分析和计算，为航天器太阳电池阵的设计和仿真提供支持[3]。

空间大型可展开式天线在近年得到应用，这些天线使用轻薄柔软、可折叠的金属网布作为反射材料，代替以前的金属薄板天线，令天线具有很高的体积收缩比，而且重量轻[4-6]。这种天线的口径通常为十几到几十米，在轨展开之后，会分时段对太阳电池阵造成遮挡，甚至完全遮挡。与其他实体遮挡不一样，金属网布由几十微米的金属丝编织而成，具有一定的透光性，且透光率与编织方式、光线入射方向都有关系。

文献[7]中，归纳了数种由网状天线造成的遮挡类型，以电池串为最小分析单元，通过实验对各类遮挡进行最坏情况分析；在整阵分析时，以最坏情况下的电池串输出特性代表同类遮挡的所有电池串的特性，绕开计算透光性遮挡的问题，为设计和任务规划提供了依据。但以最坏情况进行计算，留有较大余量，也不适合对在轨运行进行精细分析。因此，本文将对网状天线透光性遮挡的精确计算方法展开研究。

文献[8]利用Pro/E软件计算遮挡效果图，然后用Matlab对输出图像进行检测，并分析了计算过程中的误差。但因Pro/E软件的算法和源码均不公开，只能通过图形用户界面间接调用，且无法改进用于网状结构的遮挡计算。文献[9-11]中将航天器简化为基本几何体的组合，计算简单快速，但不能计算几何体不同部位透光率不一致时的阴影图形，且无法精确计算外形复杂航天器的遮挡图形。文献[12]中将全局照明辐射法和光线跟踪算法结合，计算遥感器光照分布图，计算结果精细，但速度较慢。文献[13-14]在此基础上进行了改进补充，提高了计算速度，但均假设卫星是凸多面体并使用多面体轮廓投影法，故不能对孔状、网状结构进行计算。文献[15]中，基于三角网络模型，提出精确计算太阳电池阵上实体遮挡的方法。使用三角网络模型描述三维物体，可在大部分建模软件中方便地导入导出，通用性强且能对复杂外形进行建模。但是，对金属网布组成的可展开式天线，若仍用同样的方法对每一根金属丝线进行建模计算，会使计算量和空间占用量上万倍地增加，不具备可行性。

总的来说，目前国内外文献中已对航天器实体性遮挡开展了研究，但暂未有对网状天线透光性遮挡的研究。本文参考了其他文献对实体性遮挡研究，在文献[15]的基础上，针对金属网布组成的可展开式天线造成的透光性遮挡，提出一种适用的阴影计算方法。该方法具有以下特点：(1)可计算复杂航天器模型的遮挡；(2)对于透光性遮挡，其计算量主要增加在初始化阶段，运行时计算量增加较少，可满足实时仿真的需要；(3)能够计算航天器构件在不同姿态下的遮挡情况；(4)能输出太阳电池阵上精确的遮挡图形。

1 金属网布的构造和建模

金属网布一般由0.02到0.05毫米直径的镀镍或镀金金属丝织造而成。网孔直径与天线的工作频段有关，通常为0.5到5毫米，为达到良好的电磁反射效果，应小于电磁波波长的1/10。尽管机织方法织造的网布网面平整、网孔均匀、电磁特性好，但存在可折展性差、容易撕裂的缺点，所以一般使用针织方法织造。常见的织法有双梳经平绒和双梳缎类编织，前者适用于高频段天线，后者适用于低频段天线[16]，其结构如图1所示[17]。

针织金属网布是一种空间周期性重复的结构，显然，没有必要对整个金属网布进行建模。根据具体针织结构的特点，选定最小重复单元，对该单元进行建模即可反映整个网布特性。本文对经平绒织物进行了最小重复单元划分和建模，图2为建模软件中的最小重复单元和该单元多次复制后的网布。

2 金属网布透光率分析

2.1 参考系的确立

当光线从不同方向穿过金属网布时，光线的透过率不一样。为研究金属网布透光率的变化情况，须先确立参考系，以描述光线和金属网布在三维空间的关系。本文选择金属网布本身作为参考系，以编织时的经纬方向为X轴和Y轴方向，再根据右手法则确立Z轴方向。光线方向由球面坐标系下的(θ,φ)确定，其中θ为光线矢量在XY平面的投影与X轴正方向的夹角(即方位角)，为光线矢量与XY平面的夹角(即仰角)，如图3所示。

2.2 单元阴影的计算

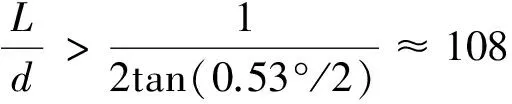
由于金属网布是最小重复单元在XY平面上的重复拼接，因此只须对最小重复单元进行分析即可得到金属网布的透光率。计算时，将金属丝视作不透光物体，根据几何投射原理，将最小重复单元投影到与光线矢量垂直的平面上。同时，将最小重复单元的外包矩形也投影到该平面上。如图4所示。统计平面上阴影的面积Ssd和矩形投影的面积Sall，则此时金属网布的透光率为

(1)

以光线方向(θ,φ)为索引，计算出所有方向下金属网布的透光率，并建立数据表格供后续计算使用。

3 可展开网状天线的遮挡计算方法

3.1 模型的数据结构

在三角网络模型中，使用三个顶点的三维坐标来描述一个三角面片的位置。对于金属网布构成部分，还需要数据描述网布方向与三角面片的关系。本文利用图3所示的XYZ坐标系，按如下方式描述两者关系：1、将网布xyz坐标系原点平移到三角面片的第一个顶点，2、计算网布XYZ坐标系中点(1,0,0)和(0,1,0)在三角网络模型中的坐标，记为V5和V6，与三角面片的三个顶点坐标{V1,V2,V3}一起组成了对三角面片空间位置和金属网布构成的完整描述。如图5所示

3.2 遮挡计算方法

太阳电池阵上的阴影使用一个二维矩阵描述，每点由一个实数R∈[0, 1] 表示相对光照强度，1代表完全没有收到遮挡，0代表完全遮挡。算法的流程如图6所示。首先使用以太阳电池阵为底的包围盒截取模型，筛选出会在太阳电池阵上形成遮挡的三角面片，按照几何关系和平行光投影原理，将三角面片投射到太阳电池阵上。对实体构件，将投影区域全标记为0，对金属网布构件，将投影区域原数值I乘以该构件在当前光线方向下的遮光率η后写回原位。

3.3 透光率的计算

金属网布的透光率与光线方向有关，第二节中用网布xyz坐标系下的方位角θ和仰角φ表示光线方向，已建立光线方向(θ,φ)与透光率η之间的表格。因此，计算出当前太阳光线方向在三角面片网布XYZ坐标系下的方位角和仰角，即可查表得到此时该三角面片的透光率。

设太阳光线方向为L(xL,yL,zL)，三角面片三个顶点为V1(x1,y1,z1)，V2(x2,y2,z2)，V3(x3,y3,z3)，描述金属网布坐标系的两个点为V5(x5,y5,z5)，V6(x6,y6,z6)。将L平移到V1为起点，则其终点VL=V1+L，将VL投影到{V1,V2,V3}所在平面，记为VLp，如图7所示。首先将{V1,V2,V3}所确定的平面写成Ax+By+Cz+D=0的一般形式。其中，

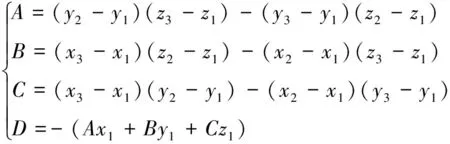
(2)

(3)

因为VLp在{V1,V2,V3}平面上，将上式代入平面方程，求得参数t后再代入式(3)，即可求得点VLp的坐标(xLp,yLp,zLp)。太阳光线方向在金属网布XYZ坐标系中的方位角θ=∠V5V1VLp。根据向量点积的定义，可求得太阳光线的方位角为

(4)

通过V1,V5,V6，计算金属网布XYZ坐标系中，点(0,0,1)在三角网络模型中的坐标V7,根据向量积的定义，得

(5)

可求得太阳光线的仰角为

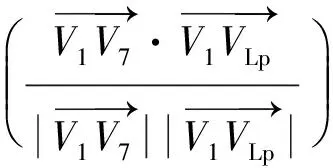
(6)

4 计算实例与分析

本文以经平绒编织金属网布构成的径向肋天线为例，计算天线在不同光照和姿态下的遮挡情况。天线模型如图8所示。

对经平绒金属网布在不同光照方向下的透光率进行计算并建立表格，结果如图9所示。

对不同姿态下的径向肋天线进行仿真计算，得到阴影图形如图10所示。

可见，当β=0°～45°时，天线右侧网布，在转动后，与太阳光线夹角较大，透光率高；左侧网布与太阳光线夹角越来越小，透光率也越来越低。当β进一步增大，左右两侧网布的投影开始重叠，阴影图中可见部分区域光照明显减少。因为经平绒编织网布在光线仰角大于30°时，透光率基本一致(参见图9)，所以只在图10(d)中观察到天线阴影从左到右有明显的透光率变化。总的来说，计算方法能够体现金属网布在不同位置的透光率区别，识别透光材料和实体材料，计算出正确的天线阴影。

透光性遮挡的计算增加了仿真运算量。本文使用原算法[15]和本文算法对多种姿态下的阴影图进行了计算，计算耗时如表1所示。由于透光性遮挡需要增加一些几何向量运算，所以计算耗时比原算法增加了15.5%，但每步计算时间仍保持在1 s以内，可以满足实时仿真的要求。

表1 仿真耗时对比Table 1 Comparison of computation time

5 实验验证

为验证透光率计算方法的准确性，本文搭建了测试平台(图11)对高频段镀金钼丝网(图12)在不同入射角度下的透光率进行了测试。

由于双轴转台的转轴与前文中方位角θ、仰角φ的转轴不一致，为了便于测试和绘图，实验和图表中按双轴转台的两个转角依次调整测试，后续数据处理中再转换为θ、φ角查表求出仿真结果与实验数据相比较。从图13中可以看出，在不同角度下，仿真和实验得到的透光率基本一致，两者绝对误差的平均值为0.011，最大值为0.042。

6 结 论

本文提出以最小重复单元对金属网布进行三维建模，求取不同光照下金属网布透光率的方法，并在此基础上，改进原来的航天器阴影计算方法，使其能够快速准确计算含金属网布构件造成的透光性遮挡图形。以经平绒编织网布构造的径向肋天线为算例，通过仿真计算和透光率测试实验，验证了算法的准确性和实时性。为太阳电池阵设计、分析提供了依据。

[1] Capel A, Perol P. Comparative performance evaluation between the S4R and the S3R regulated bus topologies [C]. Power Electronics Specialists Conference, Canada, June 17-21, 2001.

[2] 张臻, 沈辉, 李达. 局部阴影遮挡的太阳电池组件输出特性实验研究 [J]. 太阳能学报, 2012, 33(1):5-12. [Zhang Zhen, Shen Hui, Li Da. Experimental study on characteristics of partial shaded solar module [J]. Acta Energiae Solaris Sinica, 2012, 33(1):5-12.]

[3] 李涛, 李伟, 杨雷. 一种航天器太阳电池阵供电能力计算方法 [J]. 北京航空航天大学学报, 2017, 43(7):1355-1363. [Li Tao, Li Wei, Yang Lei. A calculation method for power supply capability of spacecraft solar array [J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(7):1355-1363.]

[4] 刘明治, 高桂芳. 空间可展开天线结构研究进展 [J]. 宇航学报, 2003, 24(1):82-87. [Liu Ming-zhi, Gao Gui-fang. Advances in the study on structure for space deployable antenna [J]. Journal of Astronautics, 2003, 24(1):82-87.]

[5] Dennis S, Ann T, Rodney S, et al. Design, Integration, and Deployment of the TerreStar 18-meter Reflector [C]. 28th AIAA International Communications Satellite Systems Conference, USA,September 27-30, 2010.

[6] Fei Z, Mei C. New conceptual structure design for affordable space large deployable antenna [J]. IEEE Transactions on Antennas and Propagation, 2015, 63(4):1351-1358.

[7] 袁丽丽, 寻薇, 王利然, 等. GEO卫星网状天线遮挡对太阳电池阵输出功率影响的分析及对策 [J]. 航天器工程, 2017, 26(2):91-96. [Yuan Li-li, Xun Wei, Wang Li-ran, et al. Analysis and solution of influence on solar arrays output power by netty antenna shadow for GEO satellite [J].Spacecraft Engineering, 2017, 26(2):91-96.]

[8] 邵益凯, 丁丕满, 薛孝补, 等. 图像检测在航天器太阳帆板遮挡分析中的应用 [J]. 计算机仿真, 2016, 33(7):116-120. [Shao Yi-kai，Ding Pi-man，Xue Xiao-bu，et al. Image detection application in analysis for the shadow of spacecraft solar panel [J]. Computer Simulation, 2016, 33(7):116-120.]

[9] Marek Z. Generalized analytical solar radiation pressure modeling algorithm for spacecraft of complex shape [J]. Journal of spacecraft and rockets, 2004, 41(5): 840-848.

[10] 王开强, 李京涛, 张柏楠. 平面遮挡分析法及其在航天器气动力矩分析中的应用 [J]. 宇航学报, 2016, 37(4):381-387. [Wang Kai-qiang, Li Jing-tao, Zhang Bai-nan. A planar method for obscuration analysis and its application to aerodynamic torque analysis of spacecraft [J]. Journal of Astronautics, 2016, 37(4):381-387.]

[11] 李铁映, 杨慧, 王海红. 导航卫星光压建模及表面光学特性参数影响分析 [J]. 宇航学报, 2015, 36(6):731-738. [Li Tie-ying, Yang Hui, Wang Hai-hong. Navigation satellite solar radiation pressure modeling and analysis of the effect of surface optical parameters [J]. Journal of Astronautics, 2015, 36(6):731-738.]

[12] 叶荣, 胡勇. 空间光学遥感器太阳光照分析计算方法的研究 [J]. 红外, 2009, 30(10):27-32. [Ye Rong, Hu Yong. Study of method for analyzing and calculating solar illumination on space optical remote sensor [J]. Infrared, 2009, 30(10):27-32.]

[13] Li L, Cai B, Hu J, et al. Satellite illumination algorithm applied to panel multi-axis rotation [C]. The 2nd International Conference on Information Engineering and Computer Science, Wuhan, China, Dec 25-26, 2010.

[14] Cai B, Li L, Hu J, et al. Research on spacecraft illumination [J]. International Journal of Modern Education and Computer Science, 2011, 3(4):40-46.

[15] 李安寿, 张东来, 杨炀, 等. 一种精确计算航天器本体对太阳电池阵遮挡的方法 [J]. 宇航学报, 2013, 34(10):1403-1409. [Li An-shou, Zhang Dong-lai, Yang Yang, et al. A method for accurately calculating the shadow of solar array shaded by spacecraft itself [J]. Journal of Astronautics, 2013, 34(10):1403-1409.]

[16] 韩钟剑. 编织结构形式对网状反射面天线电性能的影响分析 [D]. 西安: 西安电子科技大学, 2010. [Han Zhong-jian. Analysis on the electric performance of mesh reflector antenna by different weaving structure patterns [D]. Xi′an: Xidian University, 2010.]

[17] 李欢, 王少鹏, 黄春良, 等. 通信卫星金属网状天线及其编织技术 [J]. 产业用纺织品, 2015, 11:21-24. [Li Huan, Wang Shao-peng, Huang Chun-liang, et al. Communications satellite metal mesh antenna and its knitting technology [J]. 产业用纺织品, 2015, 11:21-24.]