Simultaneous Effects of Impurity and Electric Field on Entropy Behavior in Double Cone-Like Quantum Dot

R.Khordad,H.R.Rastegar Sedehi,and H.Bahramiyan

1Department of Physics,College of Sciences,Yasouj University,Yasouj,Iran

2Department of Physics,Jahrom University,74137-66171 Jahrom,Iran

3Department of Optics and Laser Engineering,Marvdasht Branch,Islamic Azad University,Marvdasht,Iran

1 Introduction

As is well known,electronic and transport properties of quantum dots are quite different from those of the bulk structures.Using novel nanofabrication methods such as molecular beam epitaxy,it is possible to fabricate quantum dots with various geometrical shapes and sizes like spherical,pyramidal,ellipsoidal,lens-shaped,conelike.[1−4]

In recent years,scientists worldwide have widely focused on the electronic,transport and optical properties of double quantum dots.The various con finement potential models are used for investigating physical properties of double quantum dots.For example,Bejan and Niculescu have studied intense laser effects on the optical properties of asymmetric GaAs double quantum dots under applied electric field.[5]Chenet al.[6]have studied nonlinear optical recti fication in asymmetric double triangular quantum wells.Pettaet al.[7]have investigated manipulation of a single charge in a double quantum dot.Gormanet al.[8]have studied charge-qubit operation of an isolated double quantum dot.Recently,we have studied third-harmonic generation in a double ring-shaped quantum dot under electron-phonon interaction.[9]To more information,the reader can refer to Refs.[10–13].

During the last few years,main attention has been devoted on the subject regarding the impurity states in nanostructures.Impurity state plays an important role in semiconductor devices as it modulates the electronic properties of nanostructures.It is fully known that the binding energy of a hydrogenic impurity in a quantum well has been studied,for the first time,by Bastard.[14]The effect of impurity states on optical,electronic and transport properties of quantum dots is an interesting subject in nanostructures.The presence of impurity strongly alters the energy spectrum and physical properties of quantum dots.In addition to impurity,other external factors such as electric and magnetic fields,temperature and pressure can also distort asymmetrically the con fining potential thus modifying the physical properties of quantum dots.[15−25]

Nano statistical thermodynamics which deals with systems consisting of finite numbers of particles is an extension of classical statistical thermodynamics.For the study of small systems consisting of limited assembly of particles(or nanostructures),one needs to modify classical statistical thermodynamics and obtain the detailed information about interatomic(intermolecular)forces.[26−28]The information determines the arrangement of particles as well as the geometry of these nanostructures.The previous works have been demonstrated that the domain of validity of classical thermodynamics and Boltzmann–Gibbs statistics is restricted and as a result,a good deal of attention has been put to discuss such restrictions.[29−30]This branch of science is called Nanothermodynamic or non-extensive thermodynamic.Nanothermodynamic is an extension of the thermodynamic for macroscopic systems.

Among the thermodynamic properties,the entropy is an important property in the basic sciences such as physics and chemistry.Entropy is an elementary information concept and it shows a measure of the disorder of a system.The prediction of this property is a key factor in the design,development and operation of many industrial processes.So far,many different physical de finitions of entropy have been given.As is well known,the most popular entropy is the Shannon entropy which was introduced by Claude E.Shannon in 1948.[31]Examples of other entropies are Renyi,Landsberg–Vedral and Tsallis entropy.[32−34]Hitherto,several works have been performed to predict the entropy in nanostructures using different forms of entropy functions.The reader can refer to Refs.[35–40].

In this work,we first obtain the energy levels of double cone-like quantum dot using finite element method(FEM)in the presence of impurity and applied electric field.Then,we have studied the entropy behavior using Tsallis formalism.

2 Theory and Model

Consider a cone-like double quantum dot in which a hydrogenic donor impurity located at the positionr0.The system is under an external electric field with magnitudeFand directed along the−xdirection.Within the effective mass approximation,the Hamiltonian of the system is given by

wherem∗is effective mass of the electron andV(x,y,z)is con fining potential.This con finement potential is given by

whereV0=0.35 eV is the potential height between GaAs and Ga0.5In0.5As.

Due to the complicated form of the con finement potential and the presence of impurity,the calculation of energy levels and wave functions,analytically,is a nontrivial task.[41]Therefore,we are interested in employing the finite element method(FEM)to find wave functions and energy levels of the system.[42]Using FEM,we can get a solution when we have a complicated form for the con finement potential and external effects such as impurity,temperature,and applied electric and magnetic fields.In the following,we brie fly present the FEM to solve the Schr¨odinger equation in the Cartesian coordinates.

The finite element method(FEM)is a powerful computational technique to obtain approximate solutions of boundary value problems in basic sciences like engineering,physics,and chemistry.[43−45]We consider a volume of some material or materials having known physical properties.The volume represents the domain of a boundary value problem to be solved.We construct a grid in real space using a discrete number of points.The eigenvalues and eigenvectors of the electrons con fined in a quantum dot are evaluated solving the Schr¨odinger equation

It is to be noted that the notationφ(in,out)(i,j,k)is used aswhereare spatial spacing.The superscriptions “in” and “out” denotes the wave function inside and outside the system.

The continuity of the wave functions on the quantum dot boundary is expressed by

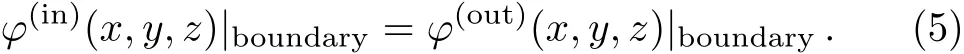
The derivative of wave functions on the quantum dot boundary is de fined as:

where the matrix elements ofA1,A2,A3,andA4are the coefficients ofφ(in)andφ(out)in Eqs.(4)–(6).The eigenvalues and eigenvectors of the system can be calculated by diagonalization of Eq.(7).It is to be noted that the strain effect has not been included in our calculations.

3 Tsallis Entropy

To overcome the restriction of classical thermodynamics and Boltzmann–Gibbs statistics,Tsallis suggested for the first time a generalized version of Boltzmann–Gibbs(BG)statistical mechanics using a new entropic form.[34]This entropy is known as an “entropy of degreeq” and depends upon a speci fic parameterq(nonextensive parameter).It is an interpolation formula that connects the Boltzmann and Gibbs entropies as the parameterq.The Tsallis entropy is given by

4 Results and Discussions

In this section,using the Tsallis formalism,the entropy is computed numerically for the double cone-like quantum dot.The parameters are used in our calculations are:q=0.9,wherem0is the mass of a free electron.

Figure 1 shows a schematic diagram for GaAs/Ga0.5In0.5As double cone-like double dot that is grown on a GaAs wet layer with thickness of 1.6 nm,radius of cross section of the bottom is 10 nm,and height is 20 nm,under negative applied electric field inxdirection.

Fig.1 (Coloronline)Schematicdiagram ofa GaAs/Ga0.5In0.5As double cone-like quantum dot that is grown on a GaAs wet layer.

Fig.2 (Color online)The entropy as a function of the temperature(a)without and(b)with central impurity for d=0.

Figures 2(a)and 2(b)display the entropy variation as a function of temperature ford=0 without and with central impurity,respectively.The curves have been plotted for different electric fields.It is seen from the figures that the entropy is decreased by enhancing the temperatures for all electric fields.We can see that the entropy reduces with increasing the electric fields.In the presence of impurity,the entropy weakly reduces.The maximum temperature in the figures is 10 K which equals with 0.86 meV.But,the potential height between GaAs and Ga0.5In0.5As isV0=350 meV.For this reason,the system disorder reduces and thereby the entropy decreases.Also,the wave function of electron becomes wider due to the increase of temperature.

In Figs.3(a)and 3(b),we have presented the entropy as a function of temperature without and with central impurity,respectively.The curves have been plotted for different electric fields withd=4 nm.It is observed from the figures that the entropy has similar behavior with previous figures whereas the entropy value decreases.Comparing Figs.2 and 3,we can see that the entropy forE=60 kV/cm has a different behavior.The probability of finding the electron forE<40 kV/cm andE>40 kV/cm is different.ForE<40 kV/cm,the electron finds in the left hand side and forE>40 kV/cm it finds in the right hand side.

Fig.3 (Color online)The same as Fig.2,but for d=4 nm.

In Fig.4,we have plotted the entropy versus temperature for o ff-center impurity withd=0.The entropy increases for the constant temperature and electric field when the impurity moves toward the system center.Also,for a constant impurity position,the entropy reduces with increasing the electric field.

Figure 5 displays the entropy as a function of temperature for different impurity positions withd=0 andE=40 kV/cm.It is observed from the figure that the entropy decreases when the temperature increases.The entropy decreases(increases)when the impurity moves toward the left hand side(right hand side).The reason for this behavior is the electric field direction.In this work,we have selected the electric field in−xdirection.

Fig.4 (Color online)Variation of the entropy versus temperature for d=0.

Fig.5 (Color online)Variation of the entropy versus temperature for E=40 kV/cm and d=0.

To show the effect of impurity position on the entropy,we have plotted the entropy as a function of impurity location in Fig.6 withT=10 K andE=40 kV/cm.The figure has been plotted for different values ofd.As seen,the entropy enhances when the separation between the quantum dotsdincreases.This means that the disorder of the system increases.

Figures 7(a)and 7(b)show the in fluence of the electric field on the entropy forT=10 K without and with impurity,respectively.With increasing the electric field,the entropy reduces for both values ofdwithout and with impurity.In the presence of an external electric field,the electron moves opposite direction of the electric field and thereby the disorder in electron movement reduces.This means that the system entropy decreases with applying the electric field.Ford=0,the entropy in the presence of central impurity has lower value whereas ford=4 nm,the entropy in the presence of impurity has higher value.It can be said that there is a competition between the effects of electric field and impurity to order the system.For low the electric fields,the impurity effect wins ford=0 whereas ford=4 nm,the electric field wins.The entropy shows asymmetric behavior as a function of electric field.The reason for this behavior may be the asymmetric behavior of electron energy as a function of electric field.To clarify this behavior,we have also plotted the electron energy in Fig.8.

In Figs.8(a)and 8(b),we have presented the electron energy as a function of the electric field forT=10 K without and with impurity,respectively.It is seen from the figure that the electron energy has asymmetric behavior as a function of electric field.This behavior is in agreement with results of Chang and Xia[51]for a pyramid quantum dot.It is found that the peak position of electronic energy is shifted toward lower electric fields with increasingdwith and without impurity.The electronic energy is decreased in the presence of impurity due to interaction between the electron and the impurity.

Fig.6 (Color online)The entropy as a function of the impurity position for E=40 kV/cm and T=10 K.

Fig.7 (Color online)The entropy as a function of the electric field(a)without and(b)central impurity for T=10 K.

Fig.8 (Color online)The energy as a function of the electric field(a)without and(b)central impurity for T=10 K.

5 Conclusions

We have studied the effects of the electric field and impurity on entropy behavior of a double cone-like quantum dot.In this regard,we have first solved the Schr¨odinger equation using the finite element method.Then,we have employed the Tsallis formalism to study entropy behavior in this system.The results show that the entropy decreases with increasing the temperature for constant impurity position and electric field.Also,the entropy reduces with increasing the electric field.The entropy is decreased with changing impurity position toward the left hand side due to the orientation of applied electric field.Tsallis formalism shows that at relatively lower temperatures like 0

[1]M.Lu,X.J.Yang,S.S.Perry,and J.W.Rabalais,Appl.Phys.Lett.80(2002)2096.

[2]R.Khordad and H.Bahramiyan,Commun.Theor.Phys.62(2014)283.

[3]R.Moradian and M.Shahrokhi,J.Phys.Chem.Solids 74(2013)1063.

[4]R.Khordad,H.Bahramiyan,and S.A.Mohammadi,Chin.J.Phys.54(2016)20.

[5]D.Bejan and E.C.Niculescu,Eur.Phys.J.B 89(2016)138.

[6]B.Chen,K.X.Guo,R.Z.Wang,et al.,Eur.Phys.J.B 66(2008)227.

[7]J.R.Petta,A.C.Johnson,C.M.Marcus,et al.,Phys.Rev.Lett.93(2004)186802.

[8]J.Gorman,D.G.Hasko,and D.A.Williams,Phys.Rev.Lett.95(2005)090502.

[9]R.Khordad,Opt.Commun.391(2017)121.

[10]C.C.Yuan,L.F.Lin,S.D.Sheng,and D.S.Ha,Chin.Phys.B 22(2013)100302.

[11]X.Q.Wang,G.Y.Yi,and W.J.Gong,Superlatt.Microstruct.doi/10.1016/j.spmi.2017.05.026.

[12]X.F.Yang and Y.S.Liu,Superlatt.Microstruct.48(2010)31.

[13]P.S.Kalpana and K.Jayakumar,Superlatt.Microstruct.doi/10.1016/j.spmi.2017.06.017.

[14]G.Bastard,Phys.Rev.B 24(1981)4714.

[15]R.Khordad and H.Bahramiyan,Eur.Phys.J.Appl.Phys.67(2014)20402.

[16]H.Damiri and H.R.Askari,Superlatt.Microstruct.101(2017)271.

[17]N.V.Agrinskaya,V.I.Kozub,N.Yu.Mikhailin,and D.V.Shamshur,Solid State Commun.260(2017)6.

[18]X.Huang and Z.Yang,Solid State Commun.204(2015)28.

[19]H.Bahramiyan and R.Khordad,Superlatt.Microstrcut.88(2015)651.

[20]R.Khordad and H.Bahramiyan,Pramana J.Phys.88(2017)50.

[21]H.Bahramiyan and R.Khordad,Opt.Quant.Electron.46(2014)719.

[22]Lafy.F.AL-Badry,Solid State Commun.254(2017)15.

[23]X.Chen and Y.Zhuang,Solid State Commun.260(2017)23.

[24]K.Sarkar,N.Kr.Datta,and M.Ghosh,Superlatt.Microstruct.50(2011)69.

[25]J.L.Xiao,Superlatt.Microstruct.90(2016)308.

[26]G.R.Vakili-Nezhaad and G.A.Mansoori,J.Comput.Theor.Nanosci.1(2004)233.

[27]H.Ra fii-Tabar and G.A.Mansoori,Nanoscience&Nanotechnology 4(2004)231.

[28]G.A.Mansoori,L.Assou fid,T.F.George,and G.Zhang,Conference on Nanodevices and Systems,Nanotech,San Francisco,CA,February 23–27(2003).

[29]Q.A.Wang,Euro.Phys.J.B 26(2002)357.

[30]Q.A.Wang,L.Nivanen,A.Le Mhaut,and M.Pezeril,J.Phys.A 35(2002)7003.

[31]C.E.Shannon,Bell Syst.Tech.J.27(1948)379.

[32]A.Renyi,inProceedings of the Fourth Berkeley Symposium on Mathematics,Statistics and Probability,University of California Press,California(1961)p.547.

[33]P.T.Landsberg and V.Vedral,Phys.Lett.A 247(1998)211.

[34]C.Tsallis,J.Stat.Phys.52(1988)479.

[35]R.Khordad and H.R.Rastegar Sedehi,Superlatt.Microstrcut.101(2017)559.

[36]R.Khordad and H.R.Rastegar Sedehi,Indian J.Phys.91(2017)825.

[37]R.Khordad,M.A.Sadeghzadeh,and A.Mohamadian Jahan-Abad,Commun.Theor.Phys.59(2013)655.

[38]M.Tiotsop,A.J.Fotue,H.B.Fostin,and L.C.Fai,Physica B 518(2017)61.

[39]R.Khordad,Int.J.Thermophys.34(2013)1148.

[40]R.Khordad,Contin.Mech.Thermodyn.28(2016)947.

[41]V.Lozovski and V.Piatnytsia,J.Comput.Theor.Nanosci.8(2011)1.

[42]R.V.N.Melnik and K.N.Zotsenko,Model.Simul.Mater.Sci.Eng.12(2004)465.

[43]M.Tsetseri and G.P.Triberis,Superlatt.Microstruct.32(2002)79.

[44]D.V.Hutton,Fundamentals of Finite Element Analysis,McGraw-Hill,New York(2004).

[45]K.Chang,J.B.Xia,and F.M.Peeters,Appl.Phys.Lett.82(2003)2661.

[46]Q.A.Wang,Phys.Lett.A 300(2002)169.

[47]Q.A.Wang and A.Le Mhaut,Chaos,Solitons and Fractals 15(2003)537.

[48]G.A.Mansoori,United Nations Tech.Monitor 53(2002)102.

[49]T.Giebultowicz,Nature(London)408(2000)299.

[50]T.L.Hill,Thermodynamics of Small Systems,Vol.I,W.A.Benjamin,New York,NY(1963);ibid.Vol.II(1964).

[51]K.Chang and J.B.Xia,Solid State Commun.104(1997)351.