一种基于盲源分离的跳频通信抗干扰方法*

朱行涛，栗铁桩，陈绍荣

（陆军工程大学通信士官学校，重庆 400035）

0 引 言

在跳频通信系统中，无论敌人采用何种形式的干扰（同频干扰[1]、宽带干扰[2]、窄带干扰[3]等），其干扰信号与通信信号一般都是统计独立的。利用信号的独立性，采用盲源分离[4-6]技术，把通信信号和干扰分离开，可以极大地抑制敌人的干扰信号，从而达到抗干扰的目的。因此，盲源信号分离理论作为一种成熟的技术手段，为解决跳频通信抗干扰问题提供了一种全新的思路[7-8]。

传统的盲分离算法是在不同的假设条件下提出的，如二阶盲辨识（Second Order Blind Identification，SOBI）算法[9]利用信号的二阶统计量，在源信号是平稳随机过程的假设下，能获得较好的分离效果，而跳频信号是时变、非平稳的随机信号[10]。因此，二阶的SOBI算法虽然复杂度低，但不适合跳频信号的分离。特征矩阵联合近似对角化（Joint Approximative Diagonalization of Eigenmatrix，JADE）算法[11]和快速独立分量分析（fast Independent Component Analysis，fast ICA）算法[12]，分别利用信号的四阶累积量和信号的非高斯最大化准则，在噪声是独立同分布（Independent Identically Distributed，i.i.d.）的假设下，能较好地分离出源信号。而当跳频通信中存在非i.i.d.噪声时，上述算法的性能会随信噪比的降低迅速退化。

针对以上问题，本文利用跳频信号的短时平稳性和有色噪声的非消失时间相关性，提出了一种基于空间预白化的跳频通信盲源分离抗干扰方法。首先，为降低有色噪声的影响，将观测数据按照跳频周期分成连续不重叠的特征窗，构建基于特征窗的联合差分相关矩阵，通过对参数化的联合差分相关矩阵进行奇异值分解（Singular Value Decomposition，SVD）得到白化矩阵，从而实现全局混合矩阵对有色噪声的正交和无偏性。然后，为消除跳频信号的非平稳特性对分离性能的影响，把白化后的观测数据在不同特征窗内得到的时滞自相关矩阵组成矩阵集合，通过对矩阵集合进行联合对角化，实现跳频信号和干扰的分离。相比于JADE算法，新算法的复杂度大大降低，同时由于采用了稳健的白化算法和分离算法，可以获得更好的分离效果，改善了跳频通信在强干扰和低信噪比情况下的误比特率性能。最后，通过仿真实验验证了新算法的有效性。

1 跳频通信盲源分离抗干扰模型

对于一个受到强干扰的跳频率通信系统，假设信道满足瞬时混合的特性，则接收信号可表示为：

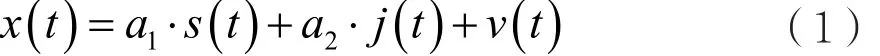
其中，s(t)为跳频信号，j(t)为干扰，v(t)为信道加性噪声，a1、a2为瞬时混合系数。在干扰很强的情况下，如果直接对接收信号进行解跳、解调，误比特率较高，跳频通信基本丧失通信能力。考虑到跳频信号s(t)和干扰j(t)是由不同发射机产生的，两者近似统计独立，可通过设计合适的盲源分离算法来实现跳频信号s(t)和干扰j(t)的分离，并将分离后的跳频信号送入解扩/解调单元，以恢复出原始信息符号。一个典型的跳频通信盲源分离抗干扰模型，如图1所示。

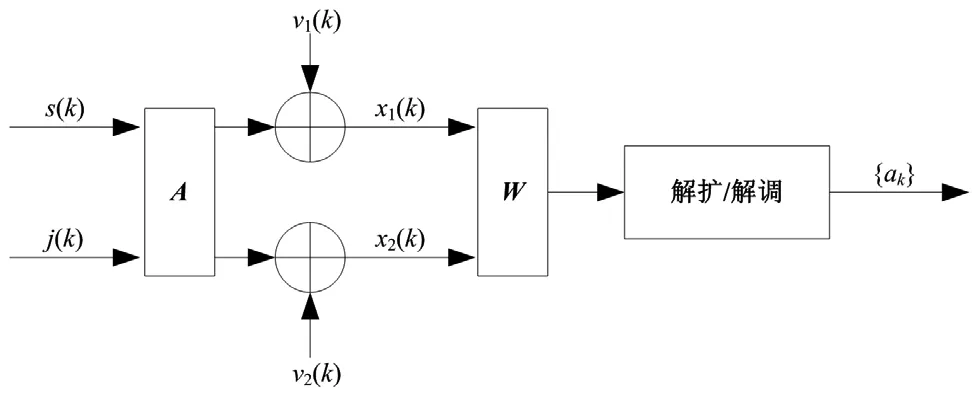
图1 跳频通信盲源分离抗干扰模型

以2根接收天线为例，接收信号矢量为X(k)=[x1(k),x2(k)]T，具有如下形式：

式中，S(k)=[s(k), j(k)]T是2路彼此独立的发射信号矢量，V(k)=[v1(k),v2(k)]T为与信号源不相关的噪声矢量，为瞬时混合系数组成的混合矩阵，反映的是信道的瞬时传输特性。

从跳频通信盲源分离抗干扰模型中可以看出，盲源分离是其中的关键点。所谓的盲源分离，就是通过寻找一个2×2阶的满秩线形变换（或分离）矩阵W，使得盲源分离后的输出矢量Y(k)=[y1(k),y2(k)]T=WX(k)中的各路分量尽可能相互独立，以实现跳频信号s(t)和干扰j(t)的分离。

2 基于空间预白化的时滞自相关矩阵集合联合对角化盲源分离算法

2.1 接收信号的空间预白化

为改善盲源分离系统的收敛特性，并消除冗余、减少噪声，避免出现病态，以提高盲源分离的性能，需首先对接收信号进行预白化[13]。传统的白化方法是通过对接收信号的自相关矩阵进行奇异值分解得到白化矩阵。但是，当信号非平稳且系统中存在非i.i.d.噪声时，该方法将失效。考虑到跳频信号的短时平稳性和有色噪声的非消失时间相关性之间的差异，构建基于特征窗的联合差分相关矩阵，利用其替代简单的自相关矩阵，通过寻找一个线性变换，使得全局混合矩阵对于加性噪声是正交和无偏的。

2.1.1 构建基于特征窗的联合差分相关矩阵

定义基于特征窗的联合差分相关矩阵：

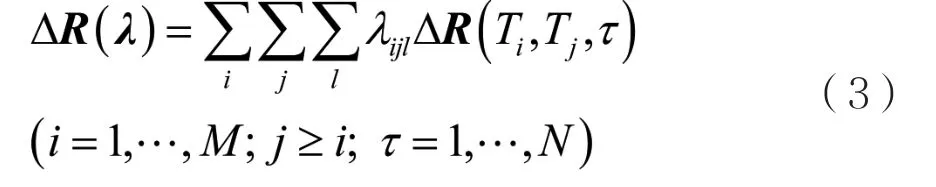
其中，λ为一组联合参数矢量，Ti和Tj是两个不重叠的等长时间窗，R(Ti,τ)表示时间窗Ti时滞τ 的 相 关 矩 阵，ΔR(Ti,Tj,τ)=R(Ti,τ)-R(Tj,τ)。 将 X(k)分成M个不重叠的时间窗，计算出ΔR^(Ti,Tj,τl)，i=1,…,M，j≥ i; l=1,…,n。

2.1.2 用联合差分相关矩阵替代自相关矩阵

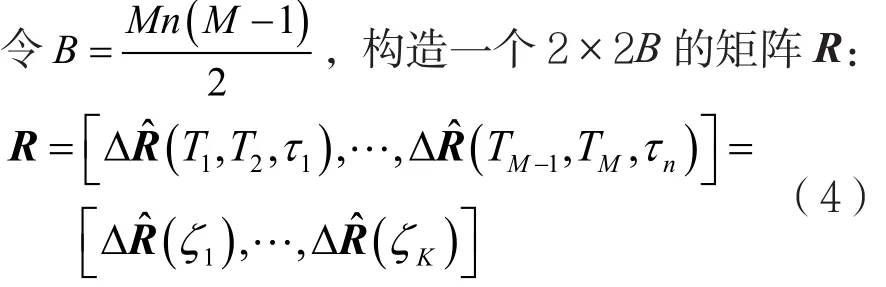
2.1.3 寻找白化矩阵

步骤1：对R进行SVD分解：

其中，U=[u1,u2]∈ R2×2，∈ R2×2B，其左 2 列包含diag{σ1,σ2}，其右2B-2列为零（当噪声功率远小于信号功率时），V∈R2B×2B是正交矩阵。

步骤2：初始化参数矢量λ=[λ1,λ2,…,λB]T，并计算：

其中，Rd=UTΔR^(ζd)U，d=1,2,…B。

步骤3：若R~非正定，则：

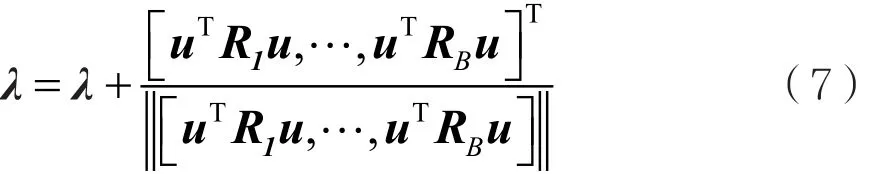
其中，u是R~的最小特征值对应的特征向量，然后返回步骤2。

若R~正定，则执行步骤4。

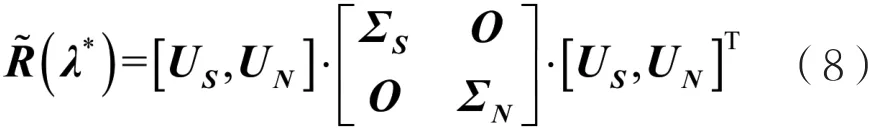
R~(λ*)进行SVD：，US包含了2个主奇值S=diag{σ1,σ2}对应的特征向量。

其中，

步骤5：使全局混合矩阵对加性噪声是正交和无偏的白化矩阵：

最终，观测信号X(k)的白化过程可用数学公式表示为：

2.2 时滞自相关矩阵集合的联合对角化

将观测数据按照跳频周期分成连续等长的时间窗，则经过预白化和时间窗处理后的跳频信号为白化的平稳信号。在时间窗Ti中，观测信号为XTi(t)=[xTi1(t),xTi2(t)]T，其自相关矩阵可表示为：

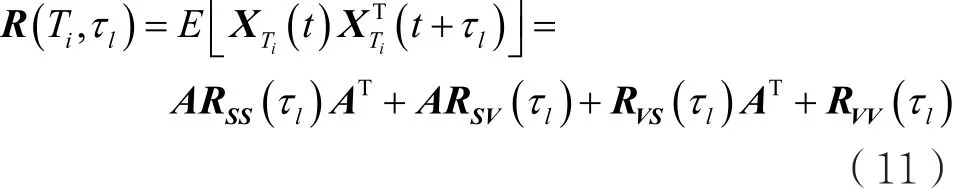
假设噪声V(t)和信号S(t)互不相关，则：

考虑到观测信号已经预白化处理，噪声功率σ2已被消除或减弱，故噪声自相关矩阵为：

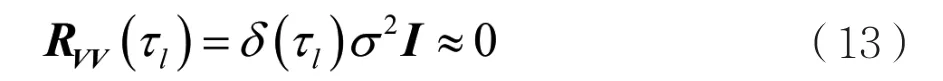
因此，时间窗Ti的自相关矩阵可近似表示为：

由于跳频信号和干扰信号近似统计独立，源信号的自相关矩阵RSS(τl)为对角矩阵，因此将每个窗里的时滞自相关矩阵R(Ti,τl),l=1,…,n组成矩阵集合ℜ={R(T1,τ1),…,R(TM,τn)}，可通过对矩阵集合进行联合对角化来实现跳频信号和干扰的分离。

算法的具体步骤如下：

步骤1：按照描述的白化方法对观测数据X(k)进行空间预白化处理X(k)=QX(k)。

步骤2：将白化后的观测数据X(k)分成M个不重叠的时间窗，估计每个时间窗内观测数据在不同时间间隔τ∈{τl|l=1,2,…,n}下的自相关矩阵

步骤 3：将 R(Ti,τl)组成矩阵集合 ℜ={R(T1,τ1),…,R(TM,τn)}，对其进行联合对角化，得到联合对角化器U。

步骤4：求得分离矩阵W和分离信号Y为：

3 性能分析

对s(t)和j(t)进行归一化处理，由式（2）可推导出有噪环境下的盲分离模型：

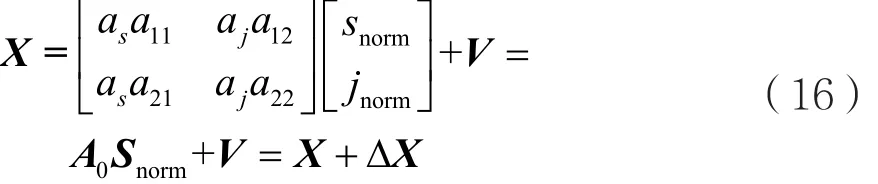
式中，snorm、jnorm分别为功率归一化后的通信信号和干扰信号，功率归一化后的等效混合矩阵为A0=[asa11,aja12;asa21,aja22]，其中as、aj为转化系数；噪声矩阵V=[v1,v2]T由多路相互独立的信道加性噪声组成，ΔX=V为由信道加性噪声引起的接收信号偏移。

理想情况下，分离矩阵W=A0-1，则在有噪环境下得到分离后的输出信号为：

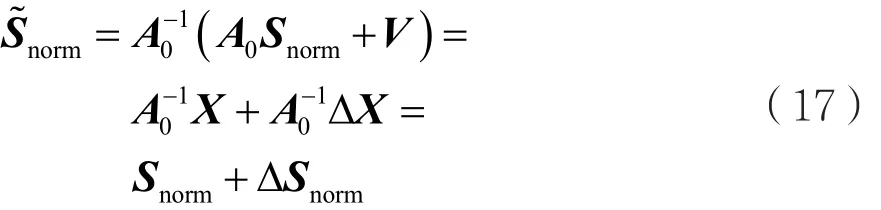
式中，ΔSnorm=A0-1V=A0-1ΔX为分离后的输出信号相对于源信号的偏移。

由矩阵范数的相容性，可得：

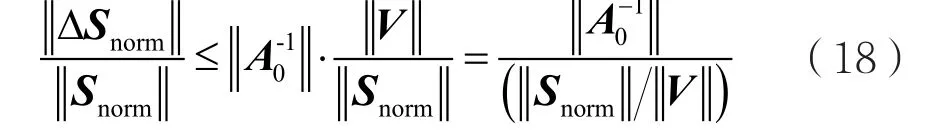
（1）与归一化信噪比[14]（Normalized Signal to Noise Ratio，NSNR）的关系

由式(18)可知：在||A0-1||一定的情况下，||ΔSnorm||/||Snorm||与||Snorm||/||V||的大小成反比。考虑到||Snorm||/||V||正比于归一化信噪比NSNR，即NSNR越小，||ΔSnorm||/||Snorm||越大，分离效果越差，抗干扰性能下降；||Snorm||/||V||越大，||ΔSnorm||/||Snorm||越小，分离效果越好，抗干扰性能提升。

综上所述，NSNR越大，分离效果越好，系统的误比特率越低；NSNR越小，分离效果越差，系统的误比特率越高。

（2）与信干比[14]（Signal to Jamming Ratio，SJR）的关系

将功率转化到混合矩阵A中后，得到等效混合矩阵A0：

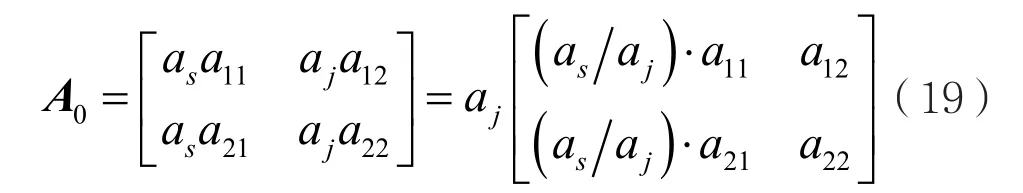
式中，a11、a12、a21、a22为原混合矩阵A的组成元素，as、aj为功率转化系数。

假设混合矩阵A和发射信号功率固定，即a11、a12、a21、a22、as为一常数，求得接收端的信干比为：

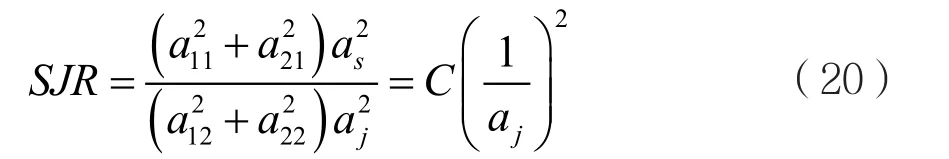
式（20）表明，在信噪比一定的情况下，接收端的SJR与aj的大小成反比，即aj→+∞，SJR越小。而当aj→+∞时，等效混合矩阵A0的病态程度（是否为列满秩）越严重。这就意味着，SJR越小，A0的病态程度越严重。

综上所述，在NSNR一定的情况下，混合信号的分离效果取决于等效混合矩阵A0的病态程度，且SJR越小，A0的病态程度越严重，混合信号的分离效果越差，造成系统的误比特率越高。

4 仿真验证

仿真参数设定如下：跳频通信盲源分离抗干扰系统采用2根天线接收，混合矩阵A=[0.461 1,0.396 7;0.438 1,-0.753 4]，期望跳频信号s(t)采用2FSK调制，2FSK信号载频中心频率fm=50 kHz，单载频的频率间隔Δf=1 kHz，信息速率Rb=1 000 bit/s，跳频频点数K=32，对应的PN序列为{0,1,…,31}间的随机整数，跳频速率为10 hop/s，跳频中心频率fh=200 kHz，单跳信号带宽Bs=5 kHz，跳频信号带宽Bt=32Bs=160 kHz，系统的采样频率fsample=1 600 kHz。仿真中，干扰j(t)主要采用全频带噪声阻塞干扰，由高斯白噪声经48阶巴特沃斯滤波器产生；加性噪声v(t)采用有色噪声，由高斯白噪声通过MA模型产生；仿真信号长度t=1 s，时间窗长度T=0.1 s，时间窗个数M=10，时间窗内的时滞次数n=4。

论文重点仿真分析了跳频盲源分离抗干扰方法在分离效果和抗干扰性能两方面的性能。其中，抗干扰性能用误比特率（Bit Error Rate，BER）来衡量，而分离性能用PI值来衡量。

PI值定义如下[15]：

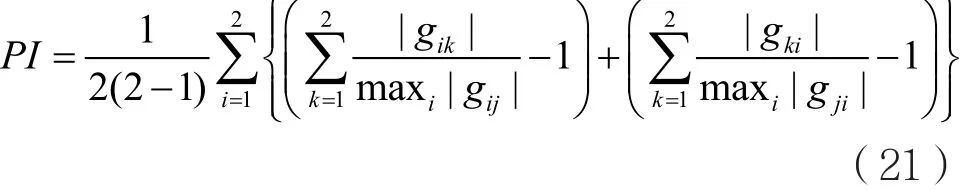
式中，gij是全局系统矩阵G=WQA的第(i, j)个元素，maxi|gij|表示G的第i行的各个元素取绝对值后的最大值。

4.1 分离效果仿真

分离性能仿真时，把信干比固定在-40 dB，而让归一化信噪比以2 dB的步长从-3 dB递增至17 dB，从而得到JADE算法、fast ICA算法和本文所提算法在梳状干扰下的PI值随NSNR变化的曲线，如图2所示。

从图2中可以看出：一方面，随着归一化信噪比的增加，3种盲源分离算法的PI值渐小，即分离效果随着NSNR的增加变好；另一方面，在NSNR较低的情况下，JADE算法和fast ICA算法的PI值接近0.8，而本文算法的PI值约为0.3，意味着本文算法在低NSNR下的分离效果要好于JADE算法和fast ICA算法。这主要是因为本文算法充分利用跳频信号的短时平稳性和有色噪声的非消失时间相关性，通过空间预白化最大限度地消弱了有色噪声的影响。

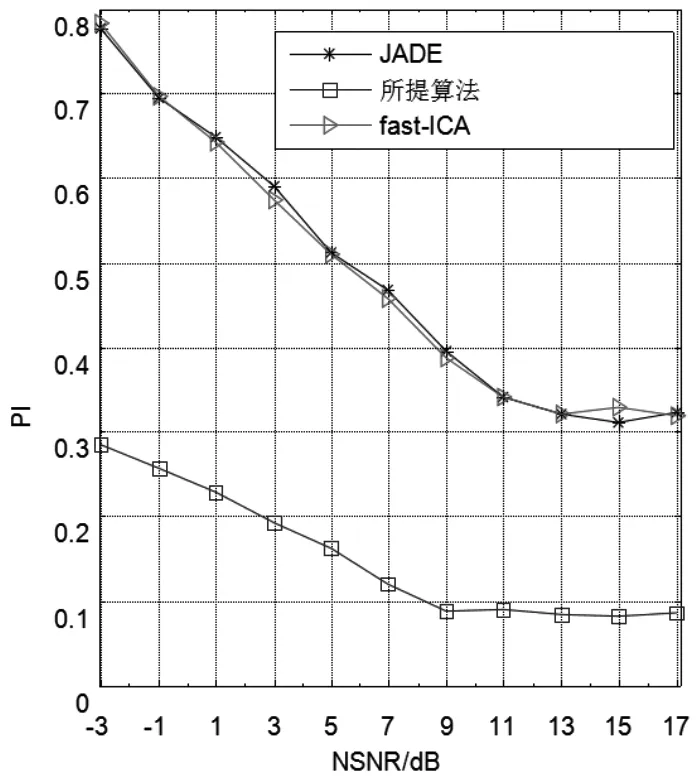
图2 PI值与NSNR关系曲线

4.2 抗干扰效果仿真

为衡量噪声功率对抗干扰效果的影响，在全频带噪声阻塞干扰下，把信干比SJR固定在-40 dB，让NSNR从-3 dB以2 dB的步长递增至17 dB，从而得到3种不同盲源分离算法（JADE算法、fast ICA算法和本文所提算法）的BER随NSNR变化的曲线，如图3所示。

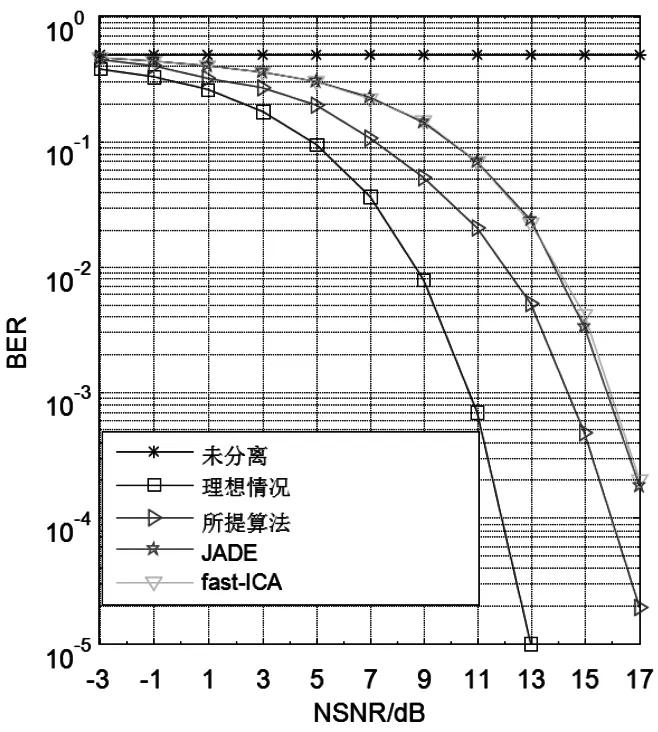
图3 BER与NSNR的关系曲线

为衡量干扰功率对抗干扰效果的影响，在全频带噪声阻塞干扰条件下，把NSNR固定为16 dB，让SJR从-100 dB以10 dB的步长递增至0 dB，从而得到3种不同盲源分离算法（JADE算法、fast ICA算法和本文所提算法）的BER随SJR变化的曲线，如图4所示。

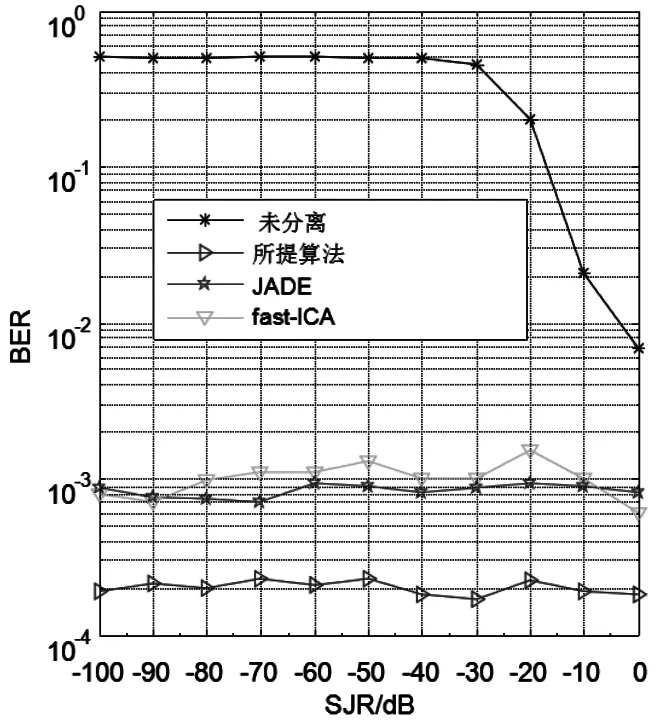
图4 BER值与SJR的关系曲线

从图4可看出：在NSNR=16 dB的情况下，采用盲源分离方法进行抗干扰后的BER，几乎不随SJR而变化，并维持在10-3～10-4的低位，通信顺畅；而对直接解扩/解调信号来说，当信干比SJR＜-30 dB时，其BER也不随SJR变化，但维持在0.5的高位，意味着此时强干扰已经超过了直扩通信的干扰容限，通信基本失效；而当SJR＞-30时，随着SJR的增加，干扰强度逐渐降低，此时直接解扩/解调信号的误比特率逐渐减小，但仍大于盲源分离抗干扰方法。

5 结 语

针对常规跳频通信难以高效抵抗人为恶意干扰和动态干扰的实际，利用源信号的统计独立性，提出了一种基于空间预白化的跳频通信盲源分离抗干扰方法。该方法基于跳频信号的短时平稳性和有色噪声的非消失时间相关性，利用自定义的联合差分相关矩阵替代传统的自相关矩阵，实现了接收信号的空间预白化，使得全局混合矩阵对有色噪声是正交和无偏的。然后，通过对白化接收信号的时滞自相关矩阵集合进行联合对角化，实现跳频信号和干扰的分离，达到抗干扰的目的。仿真结果表明：在低归一化信噪比下，新算法比JADE算法和fast ICA算法具有更好的分离效果和抗干扰性能。

参考文献：

[1] 卢志忠,周颖,黄玉.空间域相关法抗X波段航海雷达同频干扰[J].系统工程与电子技术,2017,39(04):758-767.LU Zhi-zhong,ZHOU Ying,HUANG Yu.Spatial Domain Correlation Method Anti-X-band Marine Radar Cochannel Interference[J].Journal of Systems Engineering and Electronics,2017,39(04):758-767.

[2] 刘胤廷,李秀萍,高攸纲.双天线对消技术对宽带干扰的抑制性能[J].北京邮电大学学报,2017,40(03):72-75.LIU Yin-ting,LI Xiu-ping,GAO You-gang.Suppression of Wideband Interference Through the Cancellation Technology of Dual Antennas[J].Journal of Beijing University of Posts and Telecommunicatio ns,2017,40(03):72-75.

[3] 付卫红,宋长汉,刘乃安等.基于RIE的自适应窄带干扰抑制算法[J].重庆邮电大学学报:自然科学版,2016,28(03):291-296.FU Wei-hong,SONG Chang-han,LIU Nai-an,et al.Adaptive Narrow-band Interference Suppression Algorithm Based on Recognition of Interference Existence Technology[J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2016,28(03):291-296.

[4] 许鹏飞,刘乃安,付卫红.同频同调制通信信号的卷积混合盲源分离[J].重庆邮电大学学报:自然科学版,2010,22(03):312-316.XU Peng-fei,LIU Nai-an,FU Wei-hong.Convolutive Blind Source Separation Applied to the Communication Signals that with Same Carrier Frequencies and Modulation[J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2010,22(03):312-316.

[5] Mitsui Y,Kitamura D,Takamichi S,et al.Blind Source Separation Based on Independent Low-rank Matrix Analysis with Sparse Regularization for Time-BERies Activity[C].IEEE International Conference on Acoustics,Speech and Signal Processing IEEE,2017:21-25.

[6] Ehsandoust B,Rivet B,Jutten C,et al.Nonlinear Blind Source Separation for Sparse Sources[C].Signal Processing Conference IEEE,2016:1583-1587.

[7] 于淼,王曰海,汪国富.基于独立分量分析的跳频通信抗梳状阻塞干扰方法[J].解放军理工大学学报:自然科学版,2012,13(06):593-598.YU Miao,WANG Yue-hai,WANG Guo-fu.ICA Based Anti-jamming Method of Frequency Hopping Communication against Comb Jamming[J].Journal of PLA University of Science and Technology(Natural Science Edition),2012,13(06):593-598.

[8] 于淼,王曰海,汪国富.基于BSS的跳频通信抗部分频噪声阻塞干扰方法[J].系统工程与电子技术,2013,35(05):1079-1084.YU Miao,WANG Yue-hai,WANG Guo-fu.BSS Based Anti-jamming Method for Frequency Hopping Communication against Partial-band Noise Jamming[J].Journal of Systems Engineering and Electroni cs,2013,35(05):1079-1084.

[9] Belouchrani A,Amin M G,Abed-Meraim K.Direction Finding in Correlated Noise Fields Based on Joint Block-diagonalization of Spatio-temporal Correlation Matrices[J].Signal Processing Letters IEEE,1997,4(09):266-268.

[10] 刘放,叶菲.跳频信号SPWVD参数估计方法研究[J].电脑与信息技术,2007,15(06):28-30.LIU Fang,YE Fei.Research on Estimation SPWVD Parameter of Frequency-Hopping Signal[J].Computer and information Technology,2007,15(06):28-30.

[11] Rutledge D N,Bouveresse J R.Independent Components Analysis with the JADE Algorithm[J].Trac Trends in Analytical Chemistry,2013,50(50):22-32.

[12] 王文涛,张剑云,李小波等.Fast ICA应用于雷达抗主瓣干扰算法研究[J].信号处理,2015,31(04):497-503.WANG Wen-tao,ZHANG Jian-yun,LI Xiao-bo,et al.A Study on Radar Mainlobe Jamming Suppression Algorithm Based on Fast ICA[J].Journal of Signal Processing,2015,31(04):497-503.

[13] 吴微,张帆,周志军等.基于迭代白化的含噪盲源分离技术研究[J].信息工程大学学报,2016,17(06):681-685.WU Wei,ZHANG Fan,ZHOU Zhi-jun,et al.Research on Noisy Blind Sources Separation Based on Iteration Whitening[J].Journal of Information Engineering University,2016,17(06):681-685.

[14] 朱行涛,刘郁林,何为等.基于变换域滤波的直扩通信单通道混合信号分离抗干扰方法[J].系统工程与电子技术,2016,38(10):2405-2412.ZHU Xing-tao,LIU Yu-lin,HE Wei,et al.Anti-jamming Algorithm for Direct Sequence Spread Spectrum Communication based on Source Separation of Single Channel Mixed Signal by Using Transform-domain Filter[J].Journal of Systems Engineering and Electroni cs,2016,38(10):2405-2412.

[15] 邱萌萌,周力,汪磊等.基于二阶统计和时间结构的盲信号分离方法[J].计算机应用,2014,34(09):2510-2513.QIU Meng-meng,ZHOU Li,WANG Lei,et al.Blind Separation Method for Source Signals with Temporal Structure Based on Second-order Statistics[J].Journal of Computer Applications,2014,34(09):2510-2513.