LIOUVILLE THEOREM FOR CHOQUARD EQUATION WITH FINITE MORSE INDICES∗
Xiaojun ZHAO(赵晓军)
School of Economics,Peking University,Beijing 100871,China
E-mail:zhaoxiaojun@pku.edu.cn
1 Introduction
In the studying of the existence results for non-variational elliptic equations,we usually use the topological method such as the Leray-Schauder degree theory to get the existence result.In order to apply such a theory,the most important step is to get a priori bound for the solutions.As far as we know,the blow up method is the most powerful tool in proving priori bounds for elliptic equations.The idea of the blow up method is very simple and its essence is the proof by contradiction.More precisely,suppose on the contrary that there exists a sequence of solutions{un}with Mn=un(xn)= ‖un‖L∞(Ω)→ ∞,then we make a scaling on this sequence of solutions and getClearly,after the scaling,{vn}is bounded in the L∞norm.Hence,by the regularity theory of elliptic equations,we can assume thatfor some 0 < γ < 1.Moreover,we have‖v‖L∞ =1 and it satisfies some limit equation in Ω∞,where either Ω∞=RNor Ω∞=depending on the speed of xngoes to the boundary of Ω.On the other hand,if we can prove the limit equations do not possess nontrivial solution,then we get a contradiction,hence the solutions of the original problem must be bounded.From the descriptions of the blow-up procedure,it is easy to see that in order to get a contradiction,it is essential to prove the Liouville type theorems for the limit equations.
For the above mentioned reasons,Liouville theorems for elliptic equations have drawn much attention of scientists during the past few decades and there are many results on this subject up to now.For example,in two seminal articles[13,14],Gidas and Spruck studied the nonexistence of positive solution for the following nonlinear elliptic problem

They proved that for the subcritical case,that is,1<p<,this problem possesses no positive solution.This is the so-called Liouville type theorem for positive solution of problem(1.1).Later,in order to get the priori bound for elliptic equations in bounded domains,they studied a similar equation in the half space,

Similar nonexistence result was established in[14]for positive solution of the subcritical problem in the half space.The proof of Gidas and Spruck is very complicated.Later,W.Chen and C.Li[4]simplified their proofs and got similar results by using the moving plane method.After their results,the moving plane method and its variant,the moving sphere method were widely used in proving the Liouville theorems for elliptic equations;we refer the readers to[2,3,5–8,11,19,20,23]and we can not list all of them.
We note that all the results mentioned above only claim that the subcritical problems do not possess positive solution.A natural and more complicated question is that whether these problems possess sign-changing solutions.However,this problem is completely open up to now.The main difficulty lies in that the moving plane method does not work for sign-changing solutions.Hence,we must turn to other methods.A great progress on this area is the work[1],in which the authors studied the nonexistence of solution with finite Morse index for problems(1.1)and(1.2).They proved problems(1.1)and(1.2)do not possess nontrivial bounded solution with finite Morse index provided 1<p<.This result extended the nonexistence results of positive solution to finite Morse index solution.After the work[1],there are plenty of works concerning the finite Morse index solutions for elliptic equations.For example,A.Harrabi,S.Rebhi,and S.Selmi extended their results to more general nonlinear problems in[17,18].Recently,A.Harrabi,M.Ahmedou,S.Rebhi,and A.Selmi studied the nonexistence result for Neumann boundary value problems in[15];X.Yu studied the mixed boundary problems in[24],the nonlinear boundary value problem in[25],and fractional Laplacian equation in[26].X.Zhao and X.Wang obtained the nonexistence result for Robin boundary value problems in[27].Other results can be found in[10,12,16]and the references therein.
Recently,we studied the nonexistence of positive solution for the following nonlocal equation
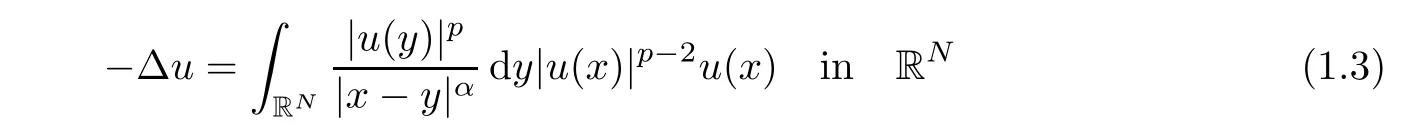
in[28].This kind of equation is usually called the Choquard type equation since in 1976,a similar equation as(1.3)was used by P.Choquard to describe an electron trapped in its own hole,in a certain approximation to Hartree-Fock theory of one component plasma[21].In some contexts,equation of type(1.3)is also called the nonlinear Schrödinger-Newton equation.In[28],we proved this equation does not possess positive solution for 0< p<by using the moving plane method.In this article,we continue to study the nonexistence of finite Morse index solution for problem(1.3).To state our result,we first define the Morse indices of solutions to problem(1.3).The Morse index of a solution u is defined by

where
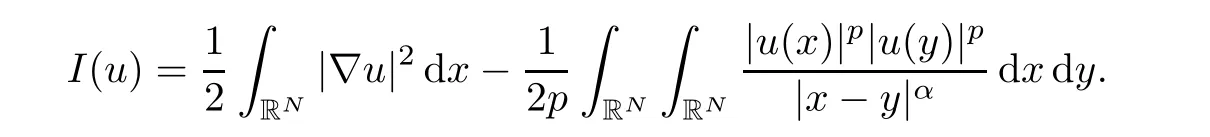
and hence

As this solution can be sign-changing,the moving plane method does not work.We use the method of energy estimation combining the Pohozaev identity to prove our result.
Now,we state our main result as the following
Theorem 1.1Suppose that N≥3,0<α<min{4,N},and u is a solution of problem(1.3)with finite Morse index,if 2< p<,then u≡0;if p=t
The rest of this article is devoted to the proof of the above theorem.In the following,we denote C by a positive constant,which may vary from line to line.
2 Proof of Theorem 1.1
In this section,we establish the nonexistence of finite Morse index solution for problem(1.3).For convenience,we denote
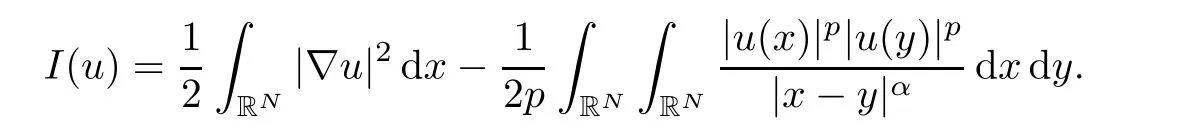
For s > 2r > 0,we define a cut-offfunction φr,sas
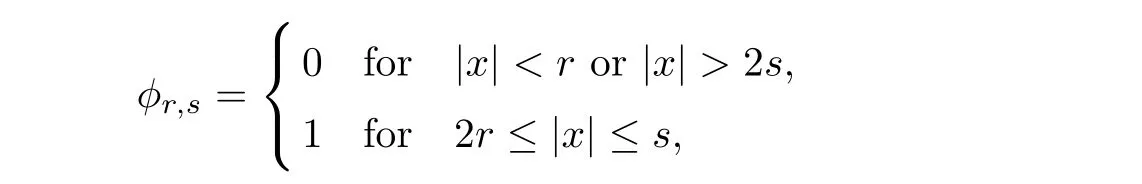
Lemma 2.1Let u be a solution of(1.3)with finite Morse index,then there exists R0>0 such that

for any R>2R0and m>0.
ProofThe proof of this lemma is the same as[27],we omit the details.
Next,we show that finite Morse index implies u satisfying some integrable conditions.More precisely,we have the following key lemma.
Lemma 2.2Under the assumptions of Theorem 1.1,if u is a solution of problem(1.3)with finite Morse index,then we have

ProofFirst,we prove thatdxdy < ∞.By Lemma 2.1,there exists R0>0,such that

for any R>2R0and m>0 to be determined later.That is

A direct calculation shows that the right hand side of equation(2.1)equals to Z
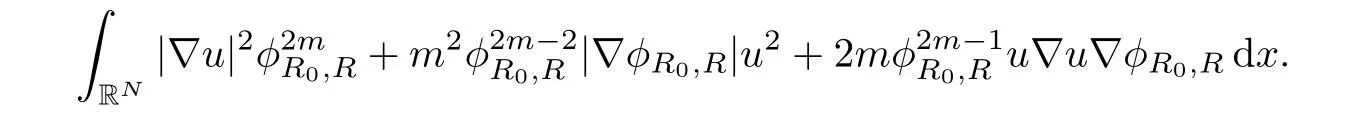
On the other hand,multiplying equation(1.3)byand integrating by parts,then we get

Insert this equation into equation(2.1),then we have
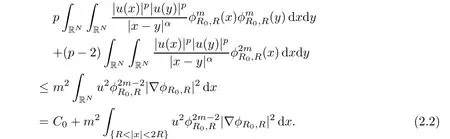
Since p≥2,in particular,we have

Suppose on the contrary thatdxdy= ∞,then for sufficiently large R,we have

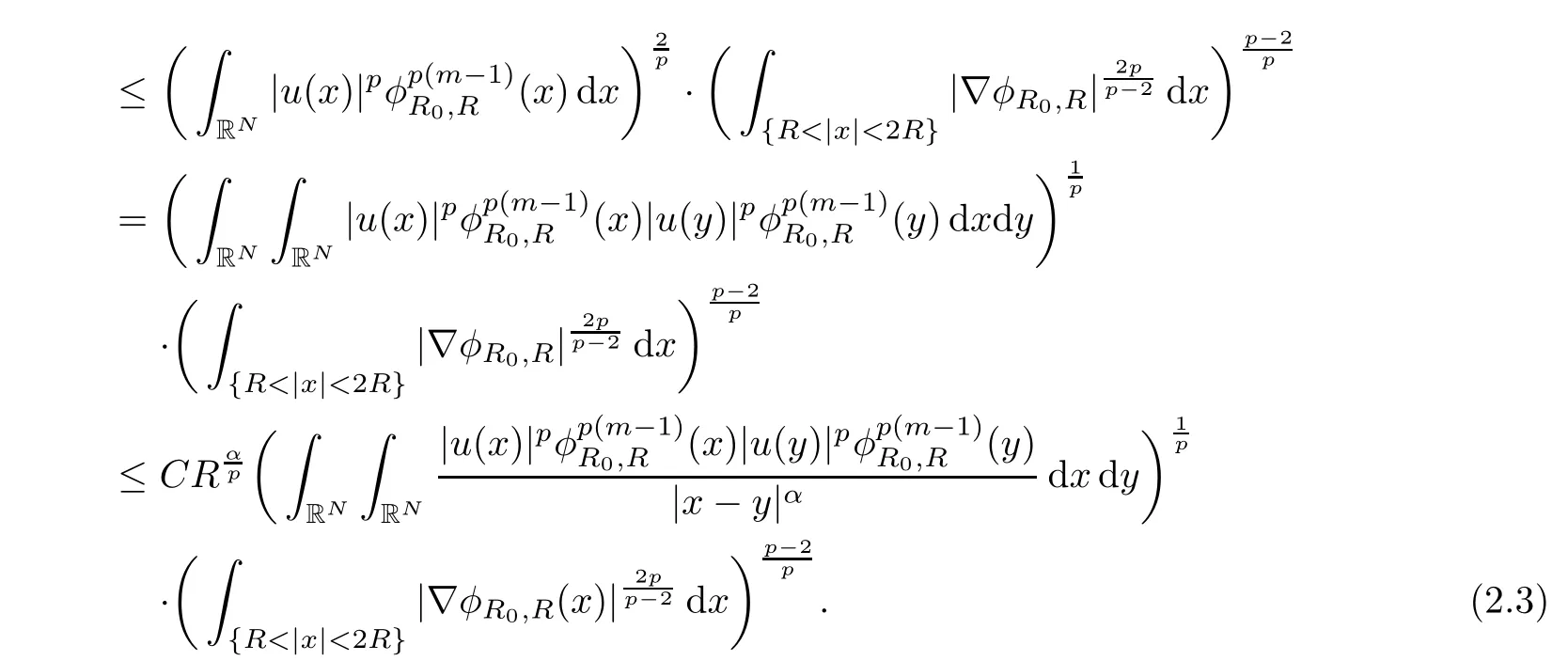
Now,we choose m to be an integer with m≥,then we have m≤p(m−1),which further implies that
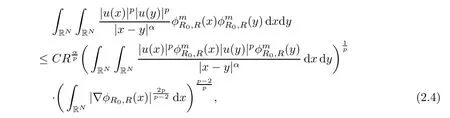
that is

Now,let R → ∞ and use the assumption that p≤,then we deduce from the above inequality that

which is a contradiction.Hence,we must have
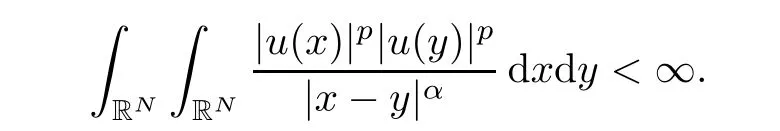
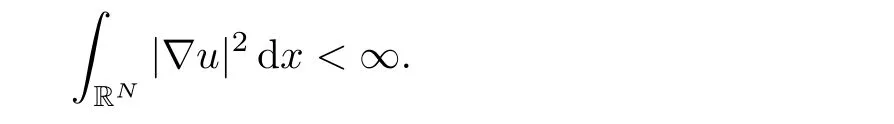
This completes the proof of this lemma.
The next Lemma is the well-known Pohozaev identity for Choquard equation,which can be found in[22].In order to keep this article self-contained,we sketch the proof of this identity.
Lemma 2.3Let u be a solution of(1.3)with
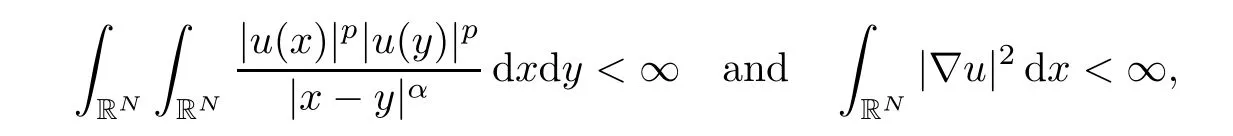
then the following identity holds
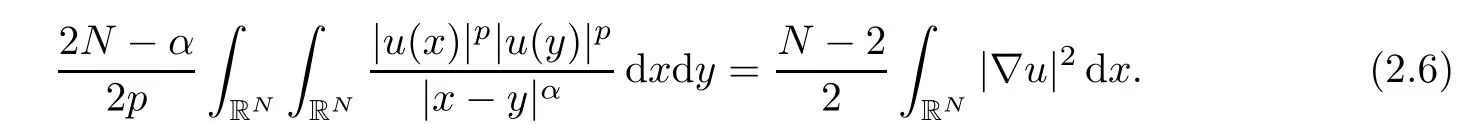
ProofWe first choose a cut-offfunction ϕ ∈ C10(RN)such that ϕ =1 in B1(0)and ϕ =0 outside B2(0).For λ ∈ (0,∞)and x ∈ RN,we define
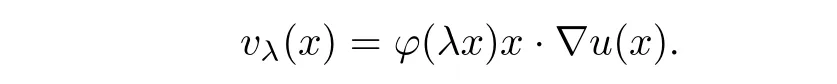
If we multiply equation(1.3)by vλand integrate by parts,then we obtain
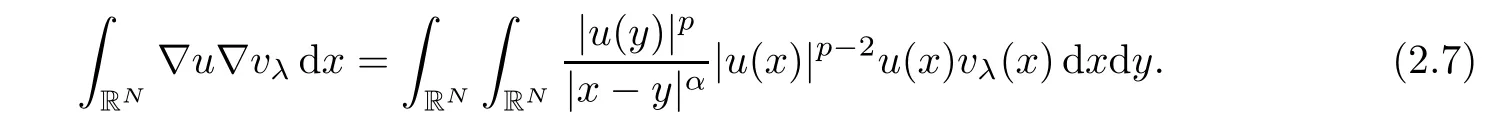
A direct calculation show that


Similarly,for the right hand side of equation(2.7),we have

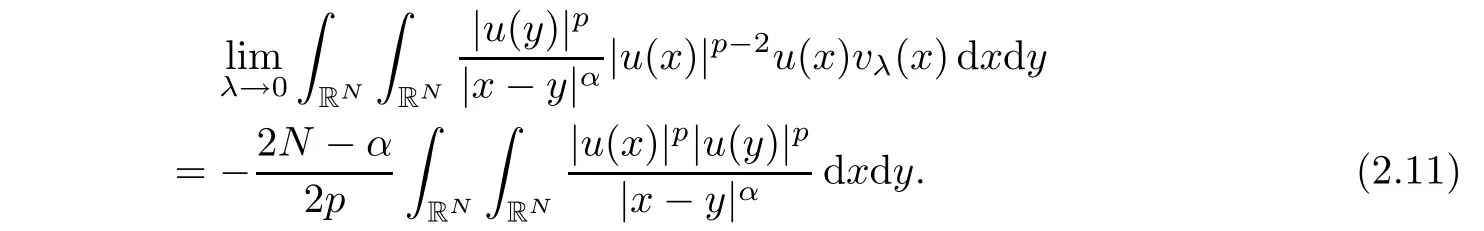
The conclusion of this Lemma follows from equations(2.7)(2.9)and equation(2.11).
With the above preparations,we can prove Theorem 1.1 now.
Proof of Theorem 1.1The proof of Theorem 1.1 is a direct consequence of Lemma 2.2 and Lemma 2.3.In fact,aswe test equation(1.3)by u(x)and integrate by parts,then we get

However,Lemma 2.3 implies that


which implies u≡0.While for p=,we have already proved that

Thus,this completes the proof of Theorem 1.1.
[1]Bahri A,Lions P L.Solutions of superlinear elliptic equations and their Morse indices.Commun Pure App Math,1992,45:1205–1215
[2]Chen W,Fang Y,Li C.Super poly-harmonic property of solutions for Navier boundary problems on a half space.J Funct Anal,2013,265:1522–1555
[3]Chen W,Fang Y,Yang R.Liouville theorems involving the fractional Laplacian on a half space.Adv Math,2015,274:167–198
[4]Chen W,Li C.Classification of solutions of some nonlinear elliptic equations.Duke Math J,1991,63:615–622
[5]Chen W,Li C,Li Y.A direct method of moving planes for the fractional Laplacian.Adv Math,2017,308:404–437
[6]Chen W,Li C,Ou B.Classification of solutions for an integral equation.Comm Pure Appl Math,2006,59:330–343
[7]Chen W,Li Y,Zhang R.A direct method of moving spheres on fractional order equations.J Funct Anal,2017,272:4131–4157
[8]Damascelli L,Gladiali F.Some nonexistence results for positive solutions of elliptic equations in unbounded domains.Rev Mat Iberoamericana,2004,20:67–86
[9]Fang Y,Chen W.A Liouville type theorem for poly-harmonic Dirichlet problems in a half space.Adv Math,2012,229:2835–2867
[10]Farina A.On the classification of solutions of the Lane-Emden equation on unbounded domains of RN.J Math Pures Appl,2007,87:537–561
[11]de Figueiredo D G,Felmer P L.A Liouville type theorem for Elliptic systems.Ann Scuola Norm Sup Pisa Cl Sci,1994,21:387–397
[12]de Figueiredo D G,Yang J.On a semilinear elliptic problem without(PS)condition.J Differential Equations,2003,187:412–428
[13]Gidas B,Spruck J.Global and local behavior of positive solutions of nonlinear elliptic equations.Comm Pure Appl Math,1981,34:525–598
[14]Gidas B,Spruck J.A priori bounds of positive solutions of nonlinear elliptic equations.Comm Part Differ Eq,1981,6:883–901
[15]Harrabi A,Ahmedou M,Rebhi S,Selmi A.A priori estimates for superlinear and subcritical elliptic equations:the Neumann boundary condition case.Manuscripta Mathematica,2012,137:525–544
[16]Harrabi A,Rahal B.On the sixth-order Joseph-Lundgren exponent.Ann Henri Poincaré,2017,18:1055–1094
[17]Harrabi A,Rebhi S,Selmi S.Solutions of superlinear equations and their Morse indices I.Duke Math J,1998,94:141–157
[18]Harrabi A,Rebhi S,Selmi S.Solutions of superlinear equations and their Morse indices II.Duke Math J,1998,94:159–179
[19]Li Y.Remark on some conformally invariant integral equations:the method of moving spheres.J Eur Math Soc,2004,6:153–180
[20]Li Y,Zhang L.Liouville-type theorems and Harnack-type inequalities for semilinear elliptic equations.J Anal Math,2003,90:27–87
[21]Lieb E H.Existence and uniqueness of the minimizing solution of Choquard’s nonlinear equation.Studies in Appl Math,1976/77,57:93–105
[22]Moroz V,Van J.Schaftingen Groundstates of nonlinear Choquard equations:existence,qualitative properties and decay asymptotics.J Funct Anal,2013,265:153–184
[23]Yu X.Liouville type theorems for integral equations and integral systems.Calc Var PDE,2013,46:75–95
[24]Yu X.Solutions of mixed boundary problems and their Morse indices.Nonlinear Analysis TMA,2014,96:146–153
[25]Yu X.Liouville theorem for elliptic equations with nonlinear boundary value conditions and finite Morse indices.J Math Anal Appl,2015,421:436–443
[26]Yu X.Solutions of fractional Laplacian equations and their Morse indices.J Differential Equations,2016,260:860–871
[27]Zhao,X,Wang X.Liouville theorem for Robin boundary value problems and finite Morse indices.J Math Anal Appl,2014,419:796–803
[28]Zhao X,Yu X.Liouville type theorem for some Choquard type equation(in Chinese).Sci Sin Math,2017,47:713–722
 Acta Mathematica Scientia(English Series)2018年2期
Acta Mathematica Scientia(English Series)2018年2期
- Acta Mathematica Scientia(English Series)的其它文章
- EXISTENCE AND BLOW-UP BEHAVIOR OF CONSTRAINED MINIMIZERS FOR SCHRÖDINGER-POISSON-SLATER SYSTEM∗
- STABILITY AND BIFURCATION ANALYSIS OF ADELAYED INNOVATION DIFFUSION MODEL∗
- ON A CLASS OF DOUGLAS FINSLER METRICS∗
- SOLUTIONS TO BSDES DRIVEN BY BOTH FRACTIONAL BROWNIAN MOTIONS AND THE UNDERLYING STANDARD BROWNIAN MOTIONS∗
- THE GLOBAL ATTRACTOR FOR A VISCOUS WEAKLY DISSIPATIVE GENERALIZED TWO-COMPONENT µ-HUNTER-SAXTON SYSTEM∗
- A NOTE IN APPROXIMATIVE COMPACTNESS AND MIDPOINT LOCALLY K-UNIFORM ROTUNDITY IN BANACH SPACES∗
