A NOTE IN APPROXIMATIVE COMPACTNESS AND MIDPOINT LOCALLY K-UNIFORM ROTUNDITY IN BANACH SPACES∗
Chunyan LIU(刘春燕)Zihou ZHANG(张子厚) Yu ZHOU(周宇)
School of Mathematics Physics and Statistics,Shanghai University of Engineering Science,Shanghai 201620,China
E-mail:cyl@sues.edu.cn;zhz@sues.edu.cn;roczhou− fly@126.com
1 Introduction
It is well known that geometric properties of Banach space have close relationship with abstract approximation problems.A typical example is that convexity in depicting the existence and uniqueness for the best approximation point in Banach spaces plays an important role;see[1–3,9,11–13]and references therein.In 1984,Megginson[7]proved that a Banach space X is midpoint locally uniformly rotund if and only if every closed ball in X is an approximatively compact Chebyshev set.It is a perfect conclusion about the relationship between approximatively compact Chebyshev sets and midpoint locally uniform rotundity in Banach spaces.In 1997,he[4]introduced midpoint locally k-uniformly rotund(MLk-UR,for short)Banach space,which is a generalization of midpoint locally uniform rotundity(MLUR,for short).Furthermore,in 2004,Xian and Li[10]introduced weak midpoint locally k-uniformly rotund(WMLk-UR,for short)Banach space,which is a generalization of weak midpoint locally uniform rotundity(WMLUR,for short).On the basis of the generalized concepts of MLUR,in this article we try to consider the relationship between MLk-UR(resp.WMLk-UR)and approximatively compact(resp.weakly compact)k-Chebyshev sets.It is obtained that a Banach space X is MLk-UR(resp.WMLk-UR)if and only if every closed ball in X is an approximatively compact(resp.weakly compact)k-Chebyshev set,which is the extension of the conclusion in[7].
We follow the standard notations in[11].For a real Banach space X,let X∗be its dual.Let S(X)and B(X)be the unit sphere and closed unit ball of X,respectively.For a subset C of X and x ∈ X,let PC(x):={y∈ C;‖x−y‖=dist(x,C)},where dist(x,C)=inf{‖x−y‖:y∈ C}.
A non-empty subset C of X is said to be approximatively(weakly)compact if for every x ∈ X and every sequencein C such that ‖x−xn‖ → dist(x,C)(such a sequence is called a minimizing sequence for x in C),thenhas a subsequence converging(weakly)to an element in C.
A set C is said to be proximinal if,for every x∈X,the set PC(x)is non-empty.The set C is said to be k-Chebyshev(resp.k-semi-Chebyshev)if dimPC(x)<k and PC(x)/=Ø(resp.dimPC(x)<k)for every x∈X,where dimPC(x)is denoted as the dimension of the linear subspace of X spanned by PC(x)−y for any y in PC(x).
A Banach space X is called k-strictly rotund if any k+1 elements x1,x2,···,xk+1of X,with

are linearly dependent.
A Banach space X is said to be MLUR(resp.WMLUR)if whenever x0is in S(X)andandare sequences in S(X)such that‖xn+yn−2x0‖→ 0,then ‖xn−yn‖→ 0(resp.xn−ynw−→0).
We then recall the concept of MLk-UR(resp.WMLk-UR).To this end,we need some preliminaries.LetDenote
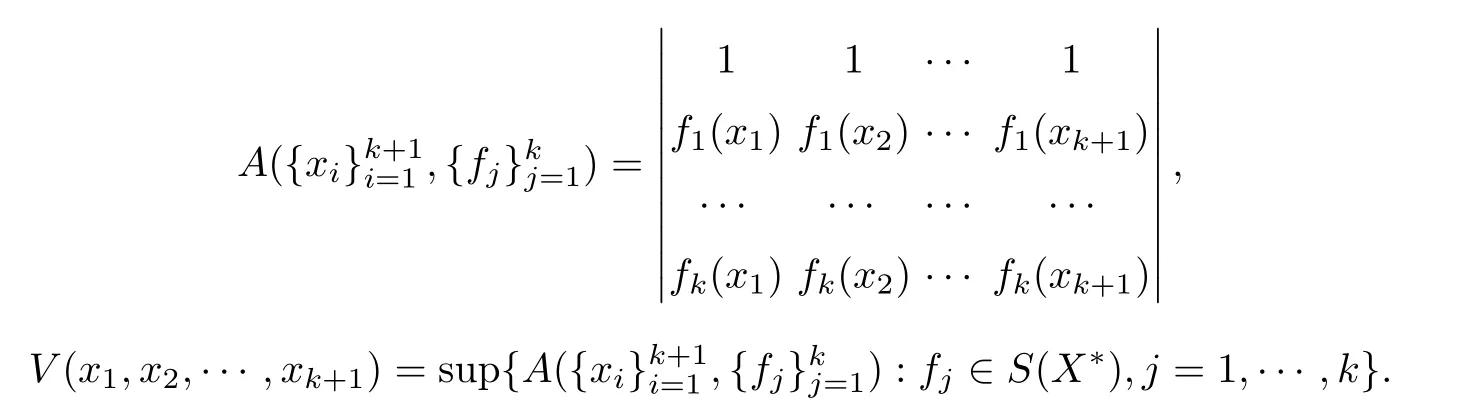
Definition 1.1([4,10]) Let k≥1 be an integer.A Banach space X is said to be MLk-UR(resp.WMLk-UR),if whenever x is in X and,i=1,···,k+1 are sequences in X such that ‖x‖ =1,→ 1,i=1,···,k+1,and→ 0,then
Remark 1.2Obviously,ML1-UR(resp.WML1-UR)space and MLUR(resp.WMLUR)space are equivalent.
2 The Main Results
To prove our main results,we need several lemmas.
Lemma 2.1Let X be a WMLk-UR space.Then,X is k-strictly rotund.
ProofWe prove this conclusion by contradiction.Suppose that X is not k-strictly rotund.Then,there exist x1,x2,···,xk+1∈ S(X)with ‖x1+x2+ ···+xk+1‖ =k+1 such that x1,x2,···,xk+1are linearly independent.We take f1,···,fk∈ S(X∗)such that fi(xi+1)=ai> 0,and fi(xj)=0,i=1,2,···,k,j=1,···,i.Therefore,we havea1···ak> 0.Let x=(x1+x2+···+xk+1)/(k+1),=xi,i=1,···,k+1.Then,x ∈ S(X),andBecause X is WMLk-UR,→0,which leads to a contradiction.
Lemma 2.2([8]) Let X be a Banach space,be a bounded sequence in X,and∈be a positive real number.Ifhas no finite ∈-net,then for any positive integers n0,k,and any x ∈ X,there exist n1(n0),···,nk(n0)> n0such that dist(xn1(n0),span{x})> ∈/2 and
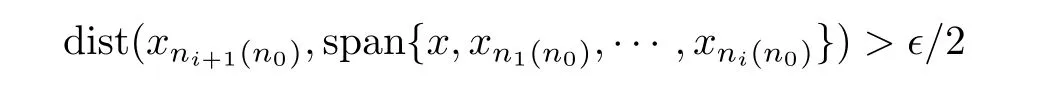
for i=1,2,···,k − 1.
Inspired by[5,Theorem 2.10.7],we have the following Lemma 2.3.
Lemma 2.3A Banach space X is k-strictly rotund if and only if every convex set in X is a k-semi-Chebyshev set.
ProofNecessity.Let C⊂X be a convex set,and x∈XC.Without loss of generality,assume that PC(x)/= Ø.Let y1,y2,···,yk+1∈ PC(x).Then,

Because X is k-strictly rotund,x−y1,x−y2,···,x−yk+1are linearly dependent.Without loss of generality,assume thatwhere α1,···,αkare real numbers.Take f∈S(X∗)such that

Obviously,f(x−yi)= ‖x−yi‖ =dist(x,C),i=1,···,k+1.Fromand dist(x,C)>0,we haveConsequently,which shows that dimPM(x)<k.
Sufficiency.If X is not k-strictly rotund,then there exists a convex set C⊂S(X),dimC≥k.Noting that PC(0)=C,we have dimPC(0)≥k,which contradicts with the condition that dimPC(0)<k.Thus,the proof is completed.
In the following,the main result is presented.
Theorem 2.4Let X be a Banach space.Then,the following statements are equivalent.
(1)X is WMLk-UR.
(2)The closed unit ball B(X)is an approximatively weakly compact k-Chebyshev set.
(3)Every closed ball B[x0,r]={x∈X:‖x−x0‖≤r}⊂X is an approximatively weakly compact k-Chebyshev set.
Proof(1)⇒(2).As X is WMLk-UR,X is k-strictly rotund by Lemma 2.1.Thus,B(X)is k-Chebyshev set by Lemma 2.3.Now,we will prove that B(X)is approximatively weakly compact.Assume that x is a point in XB(X),and{xn}∞n=1⊆ B(X)is a minimizing sequence for x.The immediate goal is to prove that{xn}∞n=1is weakly compact.
Noting that

we get
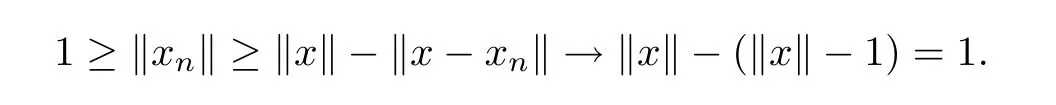
Case 1‖x‖≤ 1+

Take fn1(m),···,fnk(m)∈ S(X∗)such that

and

i=1,2,···,k − 1.Then,it yields that

Let
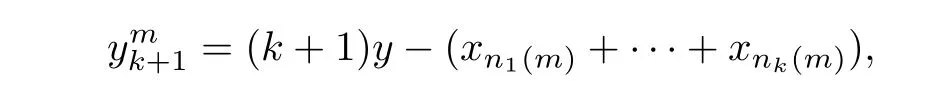
then,
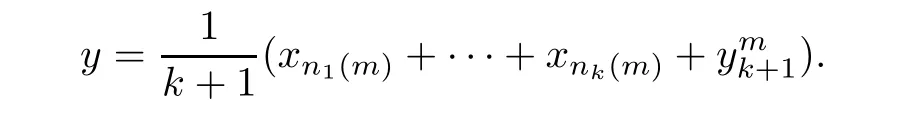
Because

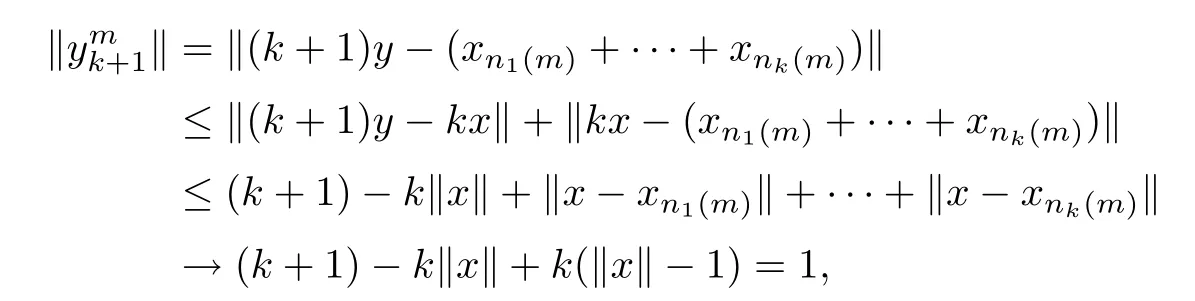
and from the WMLk-UR of X,it follows that

However,for any m∈N,we have

which leads to a contradiction.
Case 2‖x‖>1+
Set

Then,

and


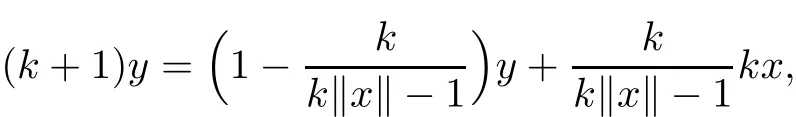
we have
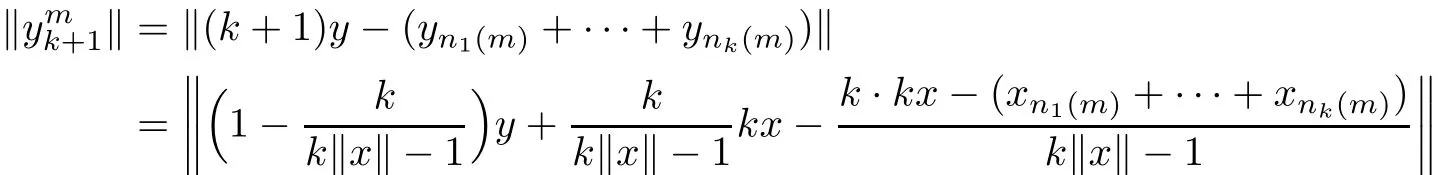

On one hand,because X is WMLk-UR,

On the other hand,

This is a contradiction.
(2)⇒ (1).Assume that X is not WMLk-UR.Then,there exist x ∈ S(X)and{xni}∞n=1⊂S(X),i=1,2,···,k+1 such that

but

for some positive realnumber∈0and some
It is easy to see that dist(k+1)x,B(X)=k.For each i(1≤i≤k+1),

and
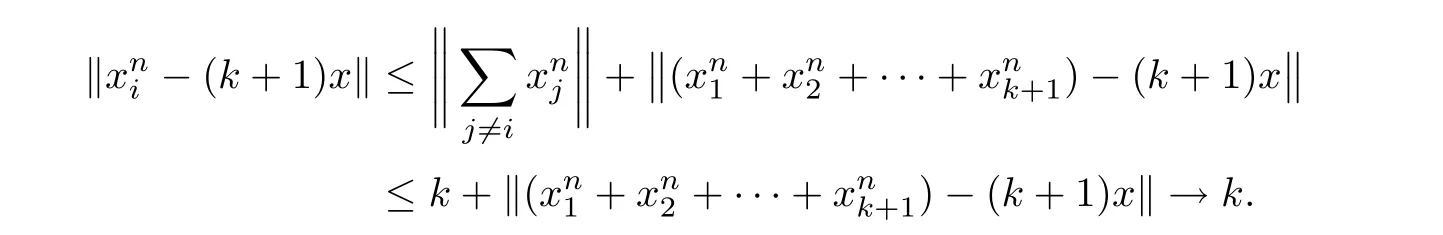
This shows that each sequenceis a minimizing sequence for(k+1)x.Then,there is a subsequence of,which converges to some xi∈ PB(X)((k+1)x)weakly.Because B(X)is a k-Chebyshev set,x1,···,xk+1are linearly dependent.Without loss of generality,we assume that

where α1,α2,···,αkare constants.We will show thatIn fact,by the Separation Theorem,there exists f∈S(X∗)such that

Noting that xi∈ B[(k+1)x,k],we obtain 1 ≤ f(xi)≤ ‖xi‖ =1.Consequently,f(xi)=1,1≤i≤k+1.It follows that
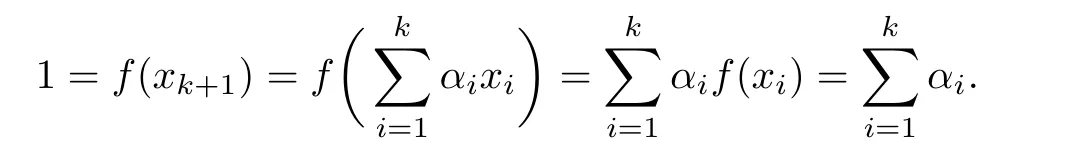
Letting n→∞,we have
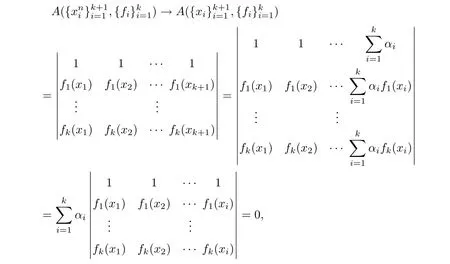
which contradicts with Inequality(2.1).
(2)⇔(3).It is obvious.
From Theorem 2.4,we obtain the following Corollary 2.5 immediately.
Corollary 2.5Let X be a Banach space.Then,the following statements are equivalent:
(1)X is WMLUR;
(2)The closed unit ball B(X)is an approximatively weakly compact Chebyshev set;
(3)Every closed ball in X is an approximatively weakly compact Chebyshev set.
Similar to the proof of Theorem 2.4,we can obtain the following Theorem 2.6.
Theorem 2.6Let X be a Banach space.Then,the following statements are equivalent:
(1)X is MLk-UR;
(2)The closed unit ball B(X)is an approximatively compact k-Chebyshev set;(3)Every closed ball in X is an approximatively compact k-Chebyshev set.
From Theorem 2.6,we obtain the following Corollary 2.7.
Corollary 2.7(Megginson) Suppose that X is a Banach space.Then,every closed ball in X is an approximatively compact Chebyshev set if and only if X is MLUR.
Remark 2.8By Theorem 2.4(resp.Theorem 2.6),we know that WMLk-UR(resp.MLk-UR)implies WML(k+1)-UR(resp.ML(k+1)-UR).However,the following Example 2.9 shows that the converse is not true.
Example 2.9For each k≥2,there exists a MLk-UR Banach space,which is not WML(k−1)-UR.
ProofLet k ≥ 2 be an integer and let i1< i2< ···< ik.For each x=(a1,a2,···)in l2,define

Lin and Yu[6]proved that(l2,‖ ·‖i1,···,ik)is k-UR.By[10],we know that(l2,‖ ·‖i1,···,ik)is MLk-UR.However,Lin and Yu[6]showed that it is not(k−1)-strictly rotund.By Lemma 2.1,(l2,‖ ·‖i1,···,ik)is not WML(k − 1)-UR. □
[1]Guirao A J,Montesinos V.A note in approximative compactness and continuity of metric projections in Banach space.J Convex Anal,2011,18:397–401
[2]Hudzik H,Wang B X.Approximative compactness in Orlicz space.J Approx Theory,1998,95:82–89
[3]Hudzik H,Kowalowski W,Lewiski G.Approximative compactness and full rotundity in Musielak-Orlicz space and Lorentz-Orlicz space.Z Anal Anwendungen,2006,25:163–192
[4]He R Y.k-strongly convex and locally k-uniformly smooth spaces.J Math(PRC),1997,17:251–256
[5]Istratescu V I.Strict convexity and complex strict convexity.New York and Basel:Marcel Dekker Inc,1984
[6]Lin B L,Yu X T.On the k-uniform rotund and the fully convex Banach spaces.J Math Anal Appl,1985,110:407–410
[7]Megginson R E.An introduction to Banach space theory.New York:Springer-Verlag,1998
[8]Nan C,Wang J.On the Lk-UR and L-kR spaces.Math Proc Cambridge Philos Soc,1988,104:521–526
[9]Singer I.The theory of best approximation and functional analysis.Philadelphis:Society for Industrial and Applied Mathematics,1974
[10]Xian J,Li Y J.k-very convex space and k-very smooth space.J Math Res Exposition,2004,24(3):483–492
[11]Zhang Z H,Shi Z R.Convexities and approximative compactness and continuity of metric projection in Banach spaces.J Approx Theory,2009,161:802–812
[12]Zhang Z H,Liu C Y.Convexity and proximinality in Banach spaces.J Funct Space Appl,2012,2012,Article ID 724120,11 pages
[13]Zhang Z H,Liu C Y,Zhou Y.Some examples concerning proximinality in Banach spaces.J Approx Theory,2015,200:136–143
 Acta Mathematica Scientia(English Series)2018年2期
Acta Mathematica Scientia(English Series)2018年2期
- Acta Mathematica Scientia(English Series)的其它文章
- EXISTENCE AND BLOW-UP BEHAVIOR OF CONSTRAINED MINIMIZERS FOR SCHRÖDINGER-POISSON-SLATER SYSTEM∗
- STABILITY AND BIFURCATION ANALYSIS OF ADELAYED INNOVATION DIFFUSION MODEL∗
- ON A CLASS OF DOUGLAS FINSLER METRICS∗
- SOLUTIONS TO BSDES DRIVEN BY BOTH FRACTIONAL BROWNIAN MOTIONS AND THE UNDERLYING STANDARD BROWNIAN MOTIONS∗
- LIOUVILLE THEOREM FOR CHOQUARD EQUATION WITH FINITE MORSE INDICES∗
- THE GLOBAL ATTRACTOR FOR A VISCOUS WEAKLY DISSIPATIVE GENERALIZED TWO-COMPONENT µ-HUNTER-SAXTON SYSTEM∗
