基于盾构施工的地表监测数据分析及建模预测

洪卓众

(龙岩市纬业测绘有限公司，福建 龙岩 364000)

1 引 言

目前城市轨道交通建设正处于加速发展阶段，越来越多的城市兴建地铁，盾构法地铁隧道施工由于具有地面作业少、对周围环境影响小、自动化程度高、施工速度快等优点，越来越受到重视和青睐，已成为地铁隧道的主要施工方法。

由于地铁隧道盾构施工一般是在地下进行，不论隧道埋有多深，都会对土体及周边建筑物产生一定程度影响。因此对盾构施工引起的地表沉降进行监测，并对监测数据进行分析，同时建立相对准确、符合规律的预测模型应用到地铁建设工程中是很有必要的。

2 盾构施工引起的地表沉降规律

2.1 盾构施工引起的地表横向沉降规律

盾构机推进过程中对周围土体产生的扰动主要分为横向与纵向，其中横向扰动范围一般在隧道轴线 20 m～30 m范围内[1]。据Peak的研究，其地表的横向变形呈正态曲线分布规律，计算公式为：

S(X)=αSmaxex2/2i2

(1)

(2)

(3)

式中：S(X)——离隧道轴线x处的地表沉降值；

Smax——横向地面最大沉降值；

x——距离隧道中线的距离；

Vloss——地层损失的体积；

i——沉降槽的宽度；

φ——土的内摩擦角；

α——最大沉降量修正系数，取值范围0.6～0.8，一般当地层损失较大时取最大值。

2.2 盾构施工引起的地表纵向沉降规律

据国内外学者的研究，对于盾构上方某一点的位移变化及变位，历时曲线可分为五个阶段：

Ⅰ 先行沉降；

Ⅱ 开挖面沉降或隆起；

Ⅲ 盾尾通过时沉降；

Ⅳ 尾部空隙沉降；

Ⅴ 后期沉降，后期沉降主要是固结沉降[2]。

通常情况下，以上五个阶段的沉降值分别占总沉降值的(0～4.5)%、(0～44)%、(15～20)%、(20～30)%和(5～30)%[3]。

3 工程实例分析

本文主要通过横向与纵向沉降规律分析深圳地铁9号线鹿丹村至人民南左右线240环至300环之间盾构施工过程中的地表沉降监测数据，该区间其隧道主要埋深在微风化变质砂岩层中，地质条件良好。

3.1 地表横向沉降规律

取该工程左线3个横断面沉降数据(具体分布如图1所示)进行分析，其中三角形为监测点，中间线为隧道中轴线，上下两边线为监测范围线。表1为3个横断面累积沉降量监测数据。图2为各监测点累计沉降量随离隧道的距离变化，横坐标为离隧道中轴线的距离，单位为m；纵坐标为累计沉降量，单位为mm。

由表1数据及图2可得出，隧道轴线上的监测点累计沉降最大，离隧道轴线距离越远，监测点累计沉降量越小，并逐渐趋于 0 mm。当离隧道距离超过 30 m时，监测点基本趋于稳定。由于实际工程地质、施工条件的复杂性、多变性，其横向地表变形规律很难完全符合Peak沉降槽理论，但是其变化趋势基本符合该理论特征。

图1 横断面监测点布置图

横断面监测数据表 表1

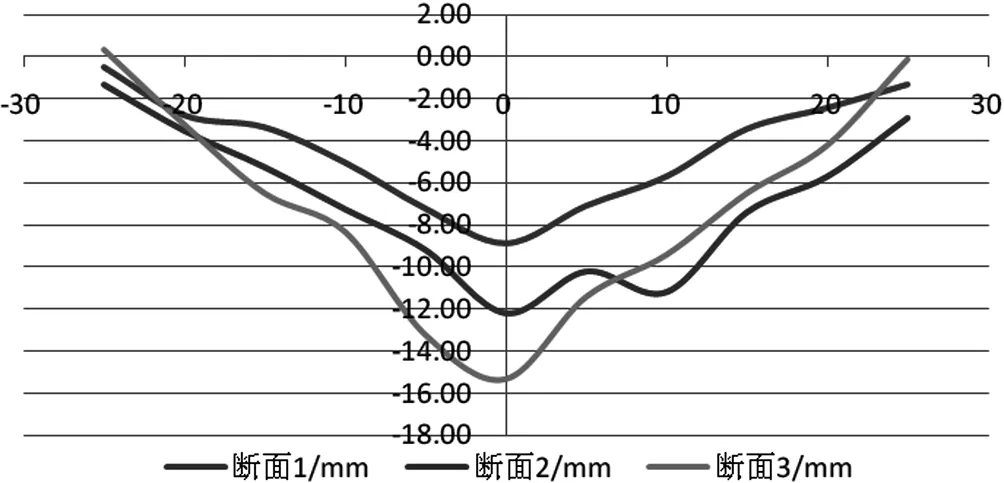
图2 横断面各监测点最大累计沉降曲线图

3.2 地表纵向沉降规律

选取两个地表监测点RD1和RD2，监测点位于隧道左右线之间(如图3所示)，监测频率为1次/天，共监测20期。表2为两个监测点累计沉降数据表，图3左图为RD1点累积沉降散点图，右图为RD2点累积沉降散点图。

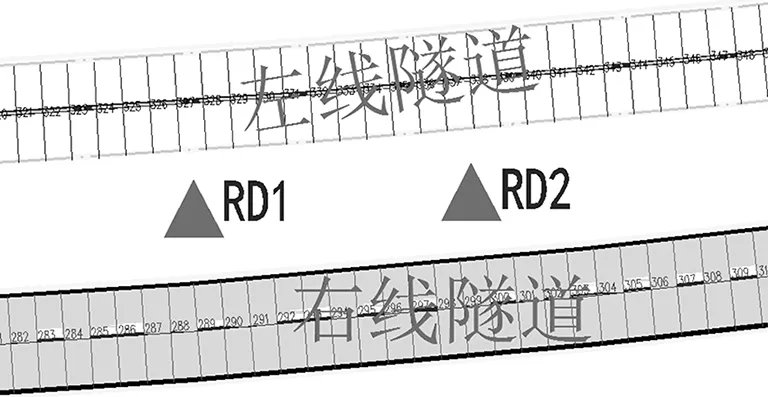
图3 RD1、RD2监测点布置图

RD1、RD2监测点各期累计沉降观测数据 表2

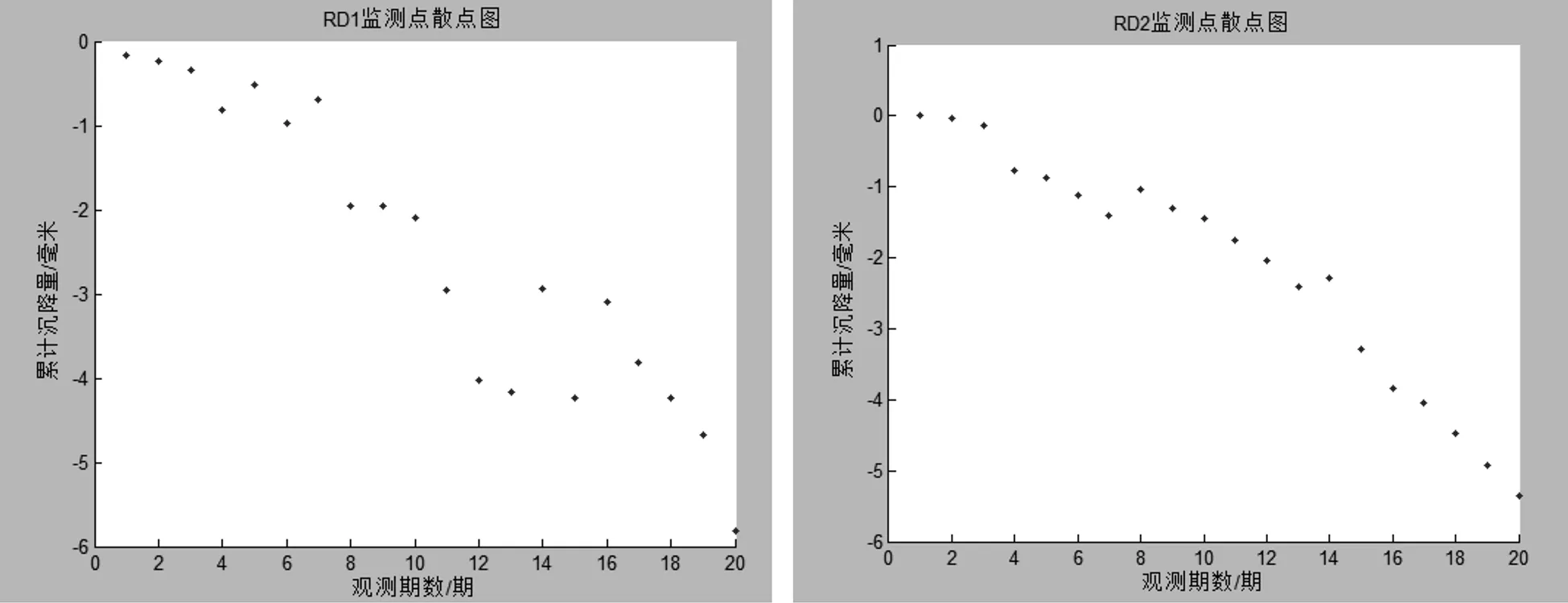
图4 监测点RD1、RD2散点图

由RD1监测点的散点图可以看出，左线隧道盾构穿过时监测点累计沉降为 6 mm，每期平均变化量为 0.3 mm，变化量比较小，不过在14期～17期间其变化有些微小波动，总体呈缓慢下降趋势。由RD2监测点的散点图可以看出，其累计沉降变化呈平稳下降趋势，累计沉降量为 5 mm。两个监测点的沉降情况可得出该项目盾构隧道施工对地表影响较小。

3.3 地表纵向沉降监测建模及预测

(1)数学建模

假定隧道左右线盾构施工对其监测点的影响相当。本文以右线隧道盾构施工过程中监测点的沉降数据作为建立模型的基础数据，然后根据该数学模型，预测左线隧道施工时地表监测点的累积沉降量并与实际采集的数据进行比对，验证该模型的预测精度。

(2)数学模型选取

①由图4可得出地表累积沉降基本成线性缓慢下沉，故本文采用一元线性回归模型(如式4所示)对该监测数据进行数学建模并预测分析。

y=a+bx+ε

(4)

式中a，b，为待估参数，x，y分别为自变量跟因变量。

②参数计算

RD1一元线性回归模型为：

y=0.4512-0.2795x

(5)

RD2一元线性回归模型为：

y=0.7188-0.2711x

(6)

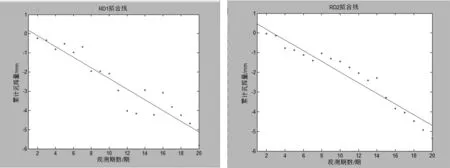
图5 RD1、RD2模型拟合图

③模型检验

本文计算采用相关系数检验方法。计算结果如表3所示。

两个模型的相关系数值 表3

拟定显著水平(一般取0.05)，查阅相关系数检验表(自由度取n-2，此处n=20)，获得临界值rα=0.444，计算结果|r|>rα，故两个监测点模型通过检验。

④模型预测

根据建立的数学模型分别对这两个监测点的21期～30期数据进行预测，其中21期～30期数据是由左线隧道盾构施工通过时影响的累计沉降值。预测结果与实际监测值的比较如表4与表5所示。

点RD1累计沉降预测值与实际值表 表4

点RD2累计沉降预测值与实际值表 表5

由表4、表5数据可得出预测偏差最大值为1.47 mm，最小值为0.03 mm，预测精度较高，满足实际工程的精度要求。

4 结 论

通过对地表监测点实际数据的分析，得出地表横向变形规律基本符合Peak公式的沉降槽理论。同时利用对地表监测点RD1与RD2的右线隧道盾构通过时影响的累计沉降数据进行一元线性回归数学建模，预测左线隧道盾构通过对地表的沉降影响，并与实际监测值进行比对，得出预测结果准确。根据其预测的结果，可以提前预知在同等地质条件及施工参数下隧道盾构施工对地表的扰动规律。

[1] 施成华，彭立敏，刘宝琛. 盾构法施工隧道纵向地层移动与变形预计[J]. 土体工程学报，2003，25(5)：585～589.

[2] 赵明阶. 土力学与地基基础[M]. 北京：人民交通出版社，2010：110～116.

[3] 侯学渊，钱达仁，杨林德. 软土工程施工新技术[M]. 合肥科技出版社，1999.

[4] 王梦恕. 21世纪我国隧道及地下空间发展的探讨[J]. 铁道科学与土程学报，2004，1(1)：7～8.

[5] 钱七虎，戎晓力. 中国地下工程安全风险管理的现状问题及相关建议[J]. 岩石力学与工程学报，2008.27(4)：64～69.

[6] 陈枫，胡志平. 盾构偏航引起的地表位移预测[Z]. 岩土力学，2004，25(9)：1427～1431.

[7] 顾硕. 地铁隧道开挖对建筑结构沉降控制分析[J]. 科技资讯．2010(12)：98～98.

[8] Attewell P B，Farmer I W. Ground disturbance caused by shield tunneling in a stiff fissured over consolidated clay[M]. In Press-Engineering Geology，1974.

[9] Atkinson J.H，Potts D M. Subsidence above shallow tunnels in soft ground[J]. Joumal of Geotechnical Engineering，1977，103(4)：307～325.

[10] Sagaseta C. Analysis of Undrained Soil Deformation Due to Ground Loss[J]. Geotechnique.1987.(37)：329～333.