基于区域似大地水准面及DEM的佛山市2000坐标系建立方案优选

杨坤，王礼江，丁孝兵，田鹏波

(佛山市测绘地理信息研究院，广东 佛山 528000)

1 前 言

目前CORS、卫星影像图和GNSS测量成果等采用的都是地心坐标系，而现有基于北京54、西安80坐标系的城市平面坐标系为参心坐标系。前者成果必须通过转换处理方可应用，而这样会导致原高精度成果精度下降，整个处理过程烦琐[1]。因此，现有的坐标系统存在局限性，已不再适应城市发展的需要。同时，根据原国家测绘局2008年第2号公告，经国务院批准，我国自2008年7月1日起，启用2000国家大地坐标系(CGCS2000)，过渡期为8年～10年；2017年3月，《国土资源部国家测绘地理信息局关于加快使用2000国家大地坐标系的通知》(国土资发〔2017〕30号)，明确要求“2018年6月底前完成全系统各类国土资源空间数据向2000国家大地坐标系转换，2018年7月1日起，全面使用2000国家大地坐标系。”因此，开展基于CGCS2000的城市新一代平面坐标系建立研究显得尤为重要。本文以佛山市为例，介绍了利用区域似大地水准面及DEM成果建立基于CGCS2000的新一代城市相对独立坐标系的优选方法，通过几种方案的比较分析，得出适合佛山市实际情况的坐标系建立方案，对其他城市开展同类工作提供借鉴。

2 高斯投影长度变形影响

投影变形是按照一定的数学模型将参考椭球面上的测量元素投影到某一平面而引起的变形。由于我国采用的是高斯投影，具有投影角度不变、图形相似以及在某点各方向上长度比相同等特点，但长度变形仅在中央子午线上为零，离中央子午线越远，长度变形越大，城市平面坐标系建立，主要解决长度变形问题。长度变形受两方面因素影响，一是将地面观测值归化至参考椭球面上，即高程归化影响；二是参考椭球面上的观测值归化至高斯平面上，即投影改正影响。

(1)地面观测值归化至参考椭球面上的长度S0按下式计算：

(1)

低海拔地区可按级数展开至一次项[2]，整理可得长度变形近似计算公式：

(2)

式中：D为地面水平观测距离，Hm为两端点平均大地高，R为基线方向法截线曲率半径。

(2)参考椭球上的边长S0归算至高斯投影面上的变形影响按下式计算：

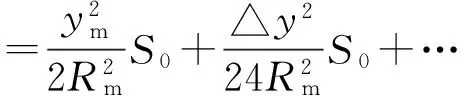
(3)

忽略二次及以上微小项的影响，得：

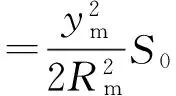
(4)

式中：ym为投影边两端点近似横坐标平均值，Rm为参考椭球面在地面边中点的平均曲率半径。

为确保投影长度变形计算的精确性，可用地面边中点所在卯酉圈半径N替代上式中的参考椭球面平均曲率半径，按下式计算：

(5)

式中：e为椭球第一偏心率，a为椭球长半轴，B为地面边中点的大地纬度。

3 利用似大地水准面及DEM确定格网大地高

建立相对独立坐标系的传统方法由于没有DEM及高程异常数据，通常采用离散的控制点或地形图提取高程数据，不能充分体现现状地形起伏情况，本文方案优选利用全市域似大地水准面成果(2′×2′)及DEM(5 m×5 m)。在不影响方案优选的情况下，为减少计算量，本文利用ArcGIS 10.2软件平台的Spatial Analyst Tools工具箱对原始DEM数据进行重采样获得了全市 500 m×500 m间隔的格网平均高程，利用自编软件采用双线性内插算法通过似大地水准面成果计算获得以上每一格网的平均大地高，如图1所示。

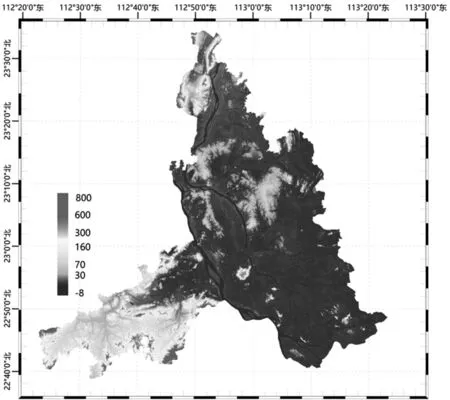
图1 地势起伏情况示意图(大地高)

4 佛山市2000坐标系建立方案

4.1 地理概况

佛山市位于东经112°23′～113°24′，北纬22°38′～23°34′，东西跨度约 103 km，南北长度约 103 km，总体上地势相对平坦，呈西高东低趋势，全市平均高程异常为 -8 m、平均大地高为 22 m，全市约63%的区域(基本为重点建设区域)大地高小于 0 m；局部区域地形起伏较大，如老香山、皂幕山海拔超过 700 m，大南山、南丹山海拔400多米，西樵山海拔300多米；全市总面积 3 858 km2。

4.2 坐标系建立方案优选

按照《城市测量规范》及《城市坐标系统建设规范》要求，城市平面坐标系选择应满足长度变形值不大于 2.5 cm/km的要求，并推荐了几种坐标系建立方法。由于佛山市地理位置情况可知，采用自定义中央子午及具有抵偿高程面的国家统一3°带高斯平面坐标系方法均无法满足现状要求，故本文仅对具有抵偿高程面的自定义中央子午线方案展开讨论，具体如下：

(1)计算流程

根据佛山市地理位置及地形起伏情况，对112°23′E～113°24′E、-20 m～100 m区间，采用穷举法，利用自编程序，按经度步长1″、大地高步长 1 m进行穷举遍历，每增加一次步长计算一次全市 500 m×500 m格网变形值，并按一定的原则对上述方案进行评价，获得最优方案。具体流程如如图2所示。

图2 计算流程图

(2)方案比较分析

按照变形值平方和最小、变形绝对值平均数最小以及变形不超限占比最大三个原则形成三套方案，采用以上计算方法，不同方案坐标系建立参数及长度变形情况如表1所示。

不同方案坐标系建立参数及长度变形情况 表1

由表1可知，方案二相对于其他方案变形不超限占比较小，不是最优方案；方案一与方案三相比，方案一变形值较小的区域最多，方案三变形不超限的区域最多，各有优点。如图3、图4所示(图中深色方格为超限位置，底图中黄色、深色为高程较高区域)，由于佛山市少部分区域高差较大，无论何种方案均难以满足高山区域长度变形不超限，但方案一在测区最西侧平坦地区仍有超限区域(面积约 40 km2)，因此，方案三为最优方案。

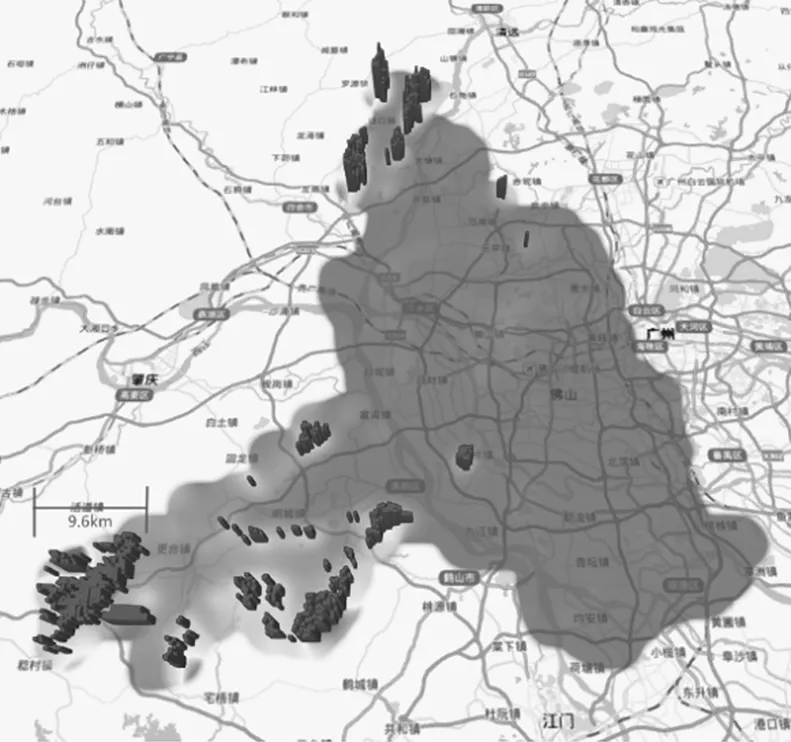
图3 方案一超限区域示意图

图4 方案三超限区域示意图

综上所述，佛山市2000坐标系建议采用基于CGCS2000椭球参数，抵偿面大地高 -11 m，采用椭球膨胀法[3]计算地方椭球参数，再通过高斯任意带投影获得平面坐标(x，y)，投影带中央子午线为112°***E。

5 结 语

相较于现行的北京54、西安80坐标系，CGCS2000的科学性、先进性和实用性是显而易见的，同时也是现有技术条件下最先进的坐标系统之一，为此各城市基于CGCS2000建立相对独立坐标系将是以后城市新一代坐标基准的发展趋势。在城市相对独立坐标系统建立工作中，由于以往没有DEM等数据，测区范围的平均高程往往是采用控制网中若干离散的控制点高程取均值或采用测区范围内的各等级比例尺地形图采样高程点进行计算，因而平均高程的取值与控制点或采样点的选择有很大关系，且带有很大的随机性[4]，而充分利用已有的城市DEM及似大地水准面成果将为准确确定独立坐标系相关参数提供便捷、可靠的途径。

[1] 郭春喜，李东. 基于CGCS2000建立城市相对独立坐标系统的方法[J]. 测绘通报，2012(10)：5～7.

[2] 宁殿民. 控制长度的变形理论和方法研究[J]. 测绘科学，2013(6)：26～28.

[3] 尹晖，李小祥，甘喆渊. 椭球变换法建立地方独立坐标系的变形研究[J]. 测绘工程，2016(2)：1～5.

[4] 王忠礼，张洪岩，侯光雷. SRTM支持下的城市地方独立坐标系的构建方法研究[J]. 北京测绘，2011(4)：5～7.

[5] 宁津生，王华，程鹏飞等. 2000国家大地坐标系框架体系建设及其进展[J]. 武汉大学学报，2015，40(5)：569～573.