EM算法在极化合成孔径雷达影像分类中的应用

隋克林

(天津市测绘院，天津 300381)

1 引 言

极化合成孔径雷达(Polarimetric Synthetic Aperture Radar，POLSAR)是获取遥感信息的一种新型技术平台。目前常用的极化方式有四种，分别是HH、HV、VH、VV。通过这四个极化通道获取的地物信息比原来单极化合成孔径雷达更加丰富、全面。极化合成孔径雷达的显著优势是它能获得目标的全极化散射特性[1]，而目标的全极化散射特性又与目标本身的形状结构、物理属性之间有着本质的联系，这为图像解译提供了丰富的信息。

目前，国内外学者已经就极化SAR影像分类做了一系列的研究。在进行SAR影像分类时，往往需要提取目标的散射特性[2]。因此，许多分类方法都是在极化分解的基础上进行的，比如采用由散射矩阵分解出的协方差矩阵或相干矩阵作为参数进行分类[3]。1997年，Cloude等人提出了一种基于部分相关目标分解的H-α分类。该方法将极化散射特性用由H和α组成的分类平面上的某一点位置来描述。但由于物体散射机理与地物目标并不是一一对应的关系，所以H-α分类结果存在地物类别模糊的问题[4]。目前主要有两种途径来弥补这一问题，一是引入其他参数，二是H、α与其他分类算法相结合[5]。引入恰当的其他参数与算法结合也能弥补H-α分类的不足[6]。2007年，曹芳、Kimura等人尝试着用总功率SPAN、极化熵H、各向异性度A和散射角α这四个参数进行全极化SAR影像的分类研究[7]，取得了较好的分类效果。该方法分类取得了一定的效果，但仍然存在海洋和植被等地物易出现错分类的现象，而且其地物细致结构也不够清晰。此外，各参数与数学算法的结合能弥补H-α分类的不足，可以尝试将各参数与FCM算法、EM算法等结合进行极化SAR影像分类。其中，EM算法是一种在缺失数据情况下对未知数据进行估计的算法，具有简单，易实现，稳定的特点[8]。

本文在H-α平面划分的基础上，引入H，α，A，SPAN参数，与EM算法结合进行极化SAR影像分类研究。

2 基本原理

2.1 EM算法原理

期望最大化(Expectation-Maximization，EM)算法是一种在数据缺失的情况下，对缺失数据进行估值的一种算法。EM算法假设数据符合某种分布，利用已知数据和最大似然方法对该分布的参数期望值进行估计，进而估计出缺失数据。

假设X为已知数据，Y是丢失数据，为分布参数。可定义函数期望似然值函数Q为：

Q(θi，θi-1)=E[logP(X，Y|θi)|X，θi-1]

(1)

式(1)中，i为第i次估值过程中的分布参数，E表示期望值，Q为数据的期望似然值。EM算法的核心思想就是通过不断地迭代，使Q最大化，以达到收敛，实现参数和丢失数据的精确估值。EM算法主要包含了两个步骤：

E步：估计参数和未知数据，计算p(Y|X，θi-1)和期望似然值；

M步：使期望似然值更新为最大值，即取θi=argmaxθQ(θi，θi-1)。

作为一个在含有隐含变量的模型中常用的估值算法，最常见的是用于高斯混合模型(Mixtures of Gaussians)下的聚类。EM算法实现简单，数值计算稳定，占资源较少，并具有良好的全局收敛性，用于图像分类已被验证能达到良好的效果[9]。

2.2 H/α/A/SPAN参数

散射矩阵S描述了地物目标的散射特性。在互易情况下，多视数据的S矩阵经过Pauli基分解得出一种散射矢量k，由散射矢量k进行相干统计平均，便可得出相干矩阵T。

(2)

式(2)中的上标“T”表示转置。

(3)

式(3)中，N为视数，H为共轭转置。

易知，T为3×3的半正定Hermit复矩阵。则矩阵T必有三个特征值，分别为λ1、λ2、λ3，其中λ1>λ2>λ3。与λi对应，T有三个特征向量：

ui=ejφi[cosαi，sinαicosβiejδi，sinαisinβiejγi]T

(4)

其中αi表示目标散射类型。

Cloude等人根据特征和散射机理，定义出地物目标的极化熵H和散射角α。其定义表达式如下：

目标极化熵H描述了地物目标散射的无序程度，散射角α则描述了地物目标的平均散射机制。极化熵和散射角的组合成的H-α分布可以描述地物目标的基本散射机制[5]。将H-α分布显示在二维平面内，该特征平面可以划分成8个有效区域，如图1所示。

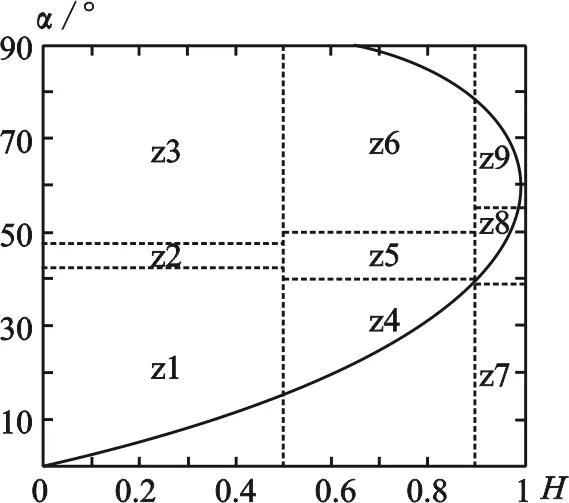
图1 H-α平面

利用H-α平面可以对SAR影像进行初步的分类，该分类方法简单，容易实现，但其分类结果往往无法清晰地区分地物，所以该方法通常作为一种快速初分类的方法。

极化熵H能反映小范围内的总体散射极值的信息，但对于熵值较小时，散射熵无法反映两个较小特征值λ2、λ3的关系，所以Cloude等人定义反熵A来反映λ2、λ3的关系。此外，总功率SPAN能反映不同地物的散射强度，有利于区分地物的纹理和边缘特征。

(5)

SPAN=λ1+λ2+λ3

(6)

本文利用H-α对SAR影像进行初分类，然后结合H，α，A，SPAN四个参数，采用EM算法对极化SAR影像进行精细地分类。

3 基于EM算法的极化SAR影像分类流程

本文将高斯模型下的EM算法结合H，α，A，SPAN四个参数应用于极化SAR影像分类。高斯模型的主要参数包括均值μ，方差σ。分类流程如图2所示。

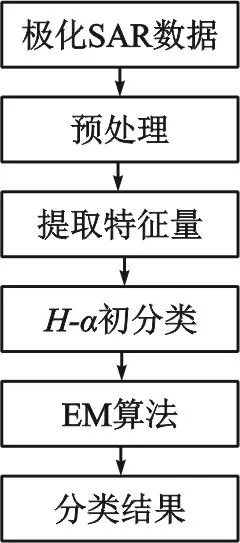
图2 EM算法分类流程

本文的EM算法分类的实验步骤如下：

(1)采用Lee滤波法3×3的窗口对SAR影像进行滤波；

(2)提取滤波后影像的极化熵H、散射角α、反熵A和功率SPAN四个参数；

(3)利用H-α的平面分布将影像初步分为八类，获得初始化的聚类中心和相关模型参数(均值μ，方差σ)；

(4)进行E步，重新估计各个模型参数；

(5)进行M步，计算当前模型参数下的似然值，与原来模型对应的似然值进行比较，将最大值赋予；

(6)判断是否满足终止条件，即是否达到最大循环次数或者似然值变化幅度是否小于阈值。若不满足，则循环进行E步、M步；若满足终止条件，则退出迭代；

(7)根据最终估算出的模型参数对影像进行判别归类。

4 实验结果分析

为验证本文所研究方法的效果，选取了NASA-JPL AIRSAR于1992年在美国加州旧金山海湾(San Francisco Bay)获取的全极化SAR影像进行实验。实验数据的大小为650×600像素。该区域主要包括城区、山区、海洋、植被、金门大桥等地物目标。图3为实验区的Pauli合成图。

图3 Pauli合成图

如图4所示，可以看出该方法对地物的细节描述比较模糊，尤其是城区和森林等部分，纹理信息缺失严重，边缘不清晰。这是因为海洋表面的极化熵值绝大部分属于中低熵值，且海洋表面相对简单平坦，其散射机制多为单次散射。而森林与城区的地表情况比较复杂，这些地区的极化熵则多属于中高熵，散射机制多是二次散射或多次散射。

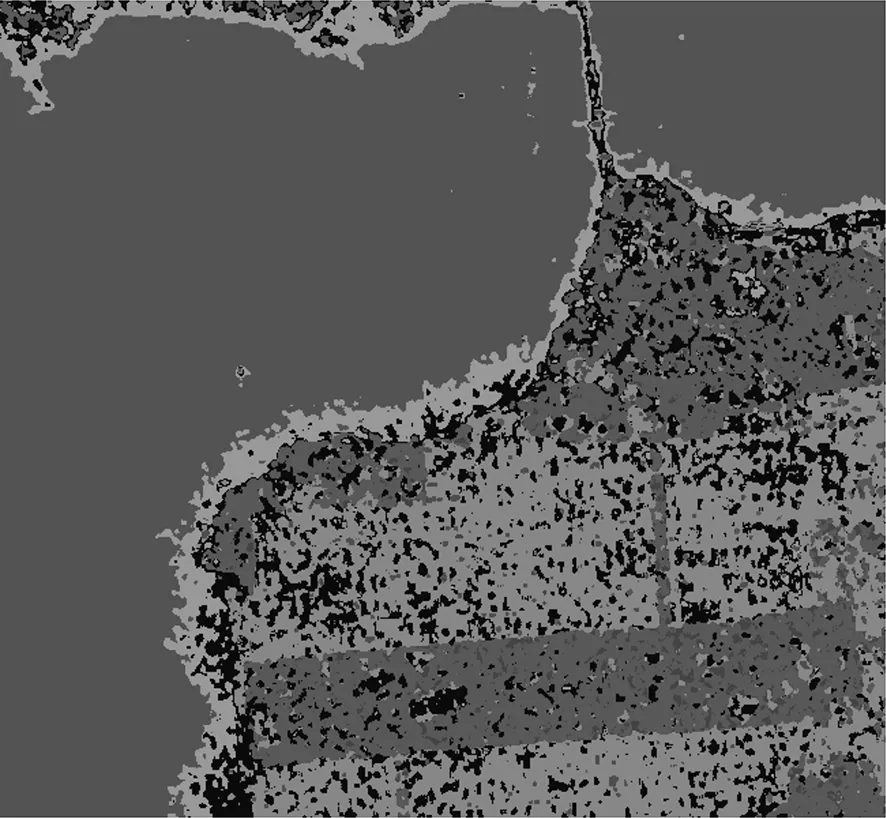
图4 H-α初分类图

Paul R，J.S Lee等人根据H-α对极化SAR影像的初分类结果，采用协方差矩阵与EM结合进行再分类，其结果如图5所示。这种分类方法取得了一定的效果。但是可以发现，采用该方法，海洋、山区和植被三类地物出现较严重的错分类现象，马球场等草地有许多误分类斑点，城区地物的纹理和细节也不够清晰。

图5 EM算法结合协方差矩阵分类图

为了进一步改善分类精度，本文采用散射熵H，散射角α，反熵A和功率SPAN四个参数与EM算法结合进行分类。因为反熵A反映了T3矩阵3个特征值中λ2与λ3的相对关系，而且当熵值较高时，反熵发挥的作用更明显。基于这个特点能更好地区分城区、植被等地物。功率SPAN反映地物目标的散射强度，通过SPAN图可以看出地物的明亮程度。将地物的物理散射机理和极化SAR影像中的空间纹理信息结合起来，能够更为细致地描述目标，获取更多的地物细节，从而有利于不同地物的区分[10]。从图5、图6的对比分析可以看出，EM算法结合H/α/A/SPAN参数的分类效果优于EM算法与协方差矩阵结合的分类效果，能够更好地区分海洋、山区和植被，错分类现象较少，如马球场等草地植被出现的错分类斑点较少，城区地物的细节和纹理也较为清晰。

图6 EM算法结合H/α/A/SPAN分类图

本文根据地物目标的实际情况，将已分的8类地物合并成4类：人工建筑、高层植被、海洋、草地和低矮植被。合并后的分类图如图7、图8所示。

图7 EM算法结合协方差矩阵分类图

图8 EM算法结合协方差矩阵分类图

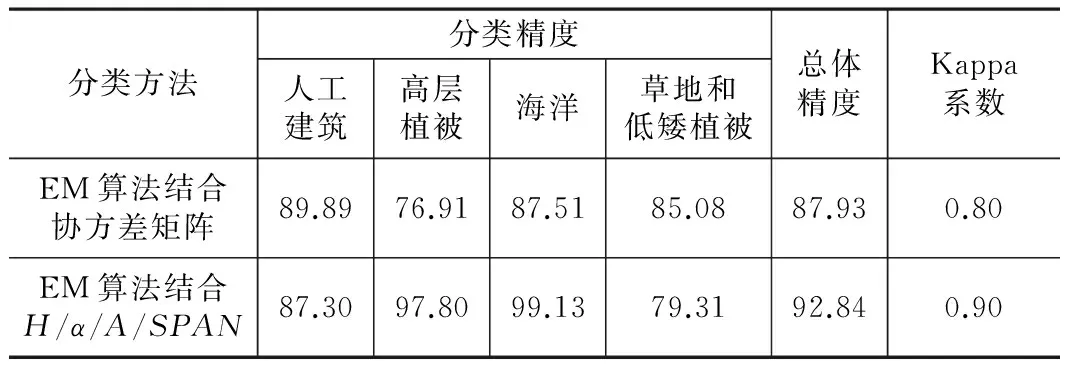
不同方法的分类精度对比(%) 表1

从表1可以看出，EM算法结合H/α/A/SPAN参数的分类结果总体精度和Kappa系数都高于EM算法与协方差矩阵结合的分类结果。

5 结 论

本文将EM算法结合散射熵H，散射角α，反熵A和功率SPAN这四个参数进行极化SAR影像分类。实验结果表明EM算法与H/α/A/SPAN参数结合比与协方差矩阵结合能更好地区分地物类别，改善分类精度。

[1] 宋才秀. 基于地物散射特性分析的机载极化SAR分类研究[D]. 长沙：中南大学，2012.

[2] 何楚，刘明，许连玉等. 利用特征选择自适应决策树的层次SAR图像分类[J]. 武汉大学学报，2012，37(1)：46～49.

[3] 赵伟颖. 极化SAR监督分类方法对植被分类效果比较分析[C]. 第九届长三角科技论·测绘分论坛，2012：117～120.

[4] 姜媛. 极化SAR图像特征提取与分类方法研究[D]. 成都：电子科技大学，2016.

[5] 周晓光，匡纲要，万建伟. 极化SAR图像分类综述[J]. 信号处理，2008，29(5)：806～811.

[6] 吕宏昌. 极化SAR图像分类研究[D]. 西安：西安电子科技大学，2015.

[7] 曹芳，洪文，吴一戎. 基于Cloude-Pottier 目标分解和聚合的层次聚类算法的全极化SAR数据的非监督分类算法研究[J]. 电子学报，2007，36(3)：543～546.

[8] 安永辉. EM算法的研究及其在文本处理中的应用[J]. 现代计算机，2013，4(上)：3～8.

[9] 邱浩. 基于EM算法的医学影像数据的分类研究[D]. 长沙：湖南师范大学，2016.

[10] 付仲良，张文元，孟庆祥. 灰度和纹理特征组合的SAR影像SVM分类[J]. 应用科学学报，2012，30(5)：498～504.