基于FPGA的列车牵引永磁同步电机半实物仿真模型研究
郑慧丽, 韩建宁, 连 蓉, 常秀丽
(中车永济电机有限公司, 陕西 西安 044500)
引言
列车牵引系统复杂且具有非线性、时变的特点,产品开发周期长,系统可靠性要求高,特别是包含多个大功率器件,分析验证的难度很大[1],为了缩短开发周期、降低设计成本,提高系统可靠性,半实物仿真技术成为不可或缺的辅助的设计验证手段。
永磁同步电机因其体积小、功率密度大、低速输出转矩大、高效率等优点受到国内外同行业工程师的广泛关注,在轨道交通行业占据日益重要的地位。在永磁同步电机为牵引电机的列车牵引系统中,运用的CPU+FPGA结构半实物仿真平台为“实际控制器+虚拟被控对象”,永磁同步电机仿真模型的准确性是牵引控制系统可靠性的关键因素[2-6]。本文主要针对高速永磁同步电机的半实物仿真建模的过程及实现方法进行介绍,离线仿真结果与电气仿真结果作对比,满足精度要求后,完成与真实的牵引控制单元的联调试验,并给出实验结果。
1 永磁同步电机数学模型
永磁同步电机半实物仿真模型基于其数学模型搭建,运用坐标变换理论对永磁同步电机解耦,使永磁同步电机可以像直流电机一样调速,给出永磁同步电机在dq轴坐标系下的电压回路方程为:
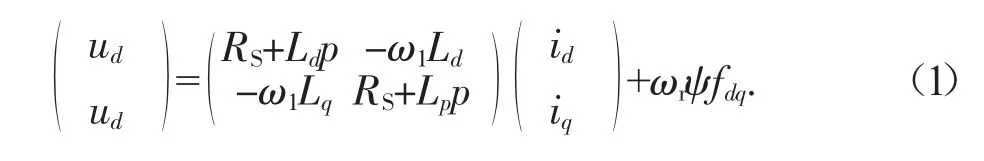
其中,ud、uq分别是dq坐标系下定子电压分量,Rs为电机定子电阻,p为微分算子,id、iq分别是定子电流分量,Ld、Lq分别为dq坐标系下的等效电枢电感,ω1永磁同步电机的同步速,ωr为dq坐标系下的电机旋转速度,ψfdq为电机的转子磁链值。ω1=ωr,即dq坐标系下的电机旋转速度与永磁同步电机的输入电压频率一致。永磁同步电机的磁链方程为:

其中 ψd、ψq均为定子磁链分量。由式(1)和(2)可以得到定子电流分别在d轴、q轴的电流分量id、iq的计算公式如式(3)所示。
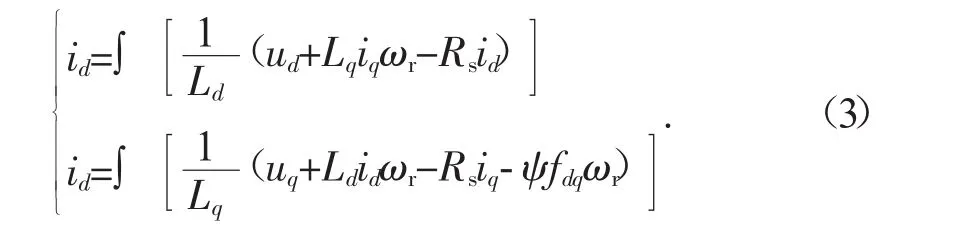
电磁转矩方程为:

将电流方程代入转矩方程可得系统运动方程为:

2 永磁同步电机模型搭建
半实物实时仿真具有严格时间边界,必须在定步长下完成仿真,定步长下要求信号在逻辑上必须同步,且实时仿真要求采用步长尽可能小,因此处理器采用FPGA芯片,利用FPGA的高速信号处理能力(运算速度可达10 ns),为仿真模型分配接口,模型编译自动生成HDL代码,运行在FPGA板卡中。
2.1 永磁同步电机仿真模型
图1为永磁同步电机d、q轴向电流和转矩计算模块,定子电流的d轴和q轴分量根据公式(4)计算得出,由公式(3)计算得出电磁转矩值。
图2为永磁同步电机半实物仿真模型,包括DQ电流和转矩计算模块、park变换、逆park变换,分块搭建模型,结构清晰,易于查错和更改。根据信号同步要求,模型中增加Delay模块,选择需要延迟的采样周期数,实现信号的并行传输,提高模型运算效率。
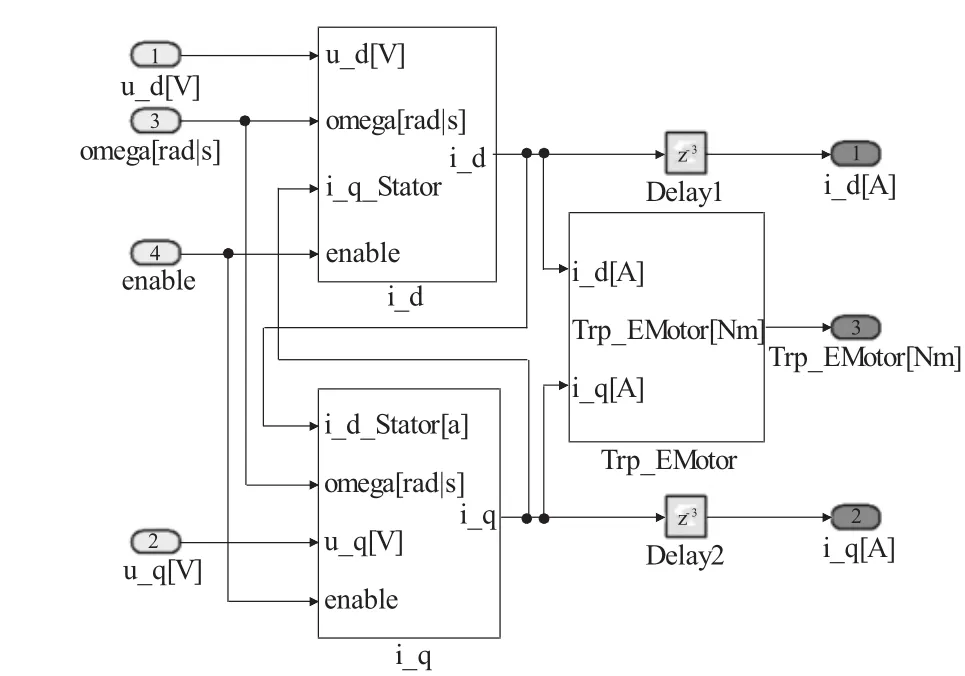
图1 定子电流和电磁转矩计算模块

图2 永磁同步电机半实物仿真模型
2.2 旋转变压器的设计
旋转变压器用于检测永磁同步电机的转速,旋变输入输出信号属于高频信号,数学模型很难实现信号的无差传输,本文选择硬件旋转变压器器件实现电机转速的转换,TCU上电就直接输出旋转变压器的激励信号,仿真模型中只需计算出电机的转子旋转角度,输出到对应的FPGA硬件接口,由硬件旋转变压器器件实现正弦、余弦的波形输出,再送到TCU的采样端口。采用硬件实现方式相对简单,精度高,易检修更换旋变模块。
仿真模型中转子位置角计算公式由式(6)可得到:

其中,θ为电机的转子旋转角度,θ0为转子旋转角度初始值,ωe为电机的电角频率。
用式(7)计算得到转子位置角模型如图3所示,输出到两个信号端口,一个用于传输信号给TCU采样,一个用于上位机上观测转子瞬时位置。
3 仿真结果与分析
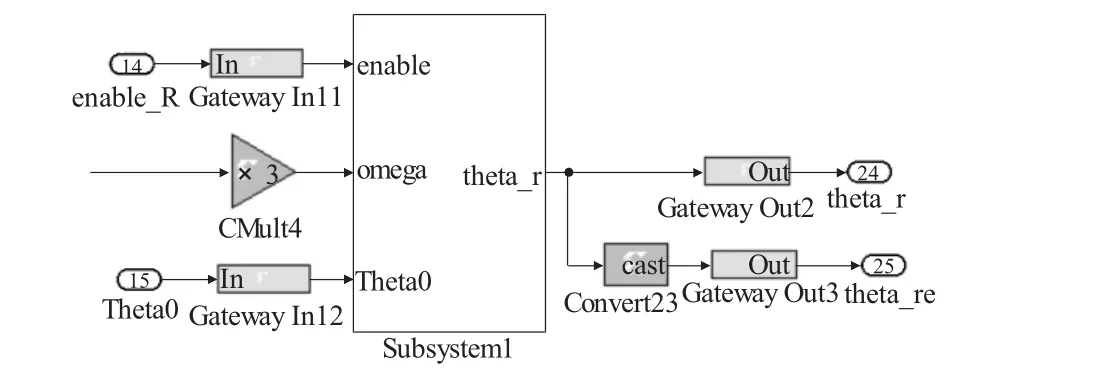
图3 转子位置角观测模块
半实物实时仿真平台中仿真机的上位机观测界面搭建方便快捷,不仅可以观测定子电流、逆变输出电压、磁链、转矩、机械角速度、电机转速等相关变量波形,其在线调参功能也极大地方便联调试验,可随时修改电机的转速、转动惯量、负载值等参数,测试验证某些参数变化对牵引系统的影响。
为保证电机模型的准确性,首先需要永磁同步电机半实物模型与标准电机模型和电气仿真模型进行离线仿真对比,验证模型精度后放入牵引系统电路中与牵引控制单元进行联调试验。
3.1 离线仿真对比
半实物仿真模型、标准电机模型、电机电气仿真模型在相同的电机参数和运行环境下离线仿真,半实物模型与标准电机模型的仿真结果误差如表1中所示,半实物模型与电机电气仿真模型的仿真结果误差如表2中所示。

表1 半实物模型与标准电机模型仿真结果误差统计表
从表1和表2的误差统计结果可以看出,搭建的半实物仿真模型在低频率段误差率很低,误差随着定子频率升高而变大,即使在最高频率点下精度也能够满足系统联调要求,因此搭建的永磁同步仿真模型具有较高的准确性。
3.2 半实物联调试验结果与分析
半实物仿真平台主要由仿真机、信号调理箱、适配箱等组成,半实物仿真模型运行在仿真机中,与牵引控制单元(TCU)的信号交互由信号调理箱完成,设置适配箱可以测试由仿真机输出的信号及TCU端的输入输出信号,方便逐级观测信号性能。
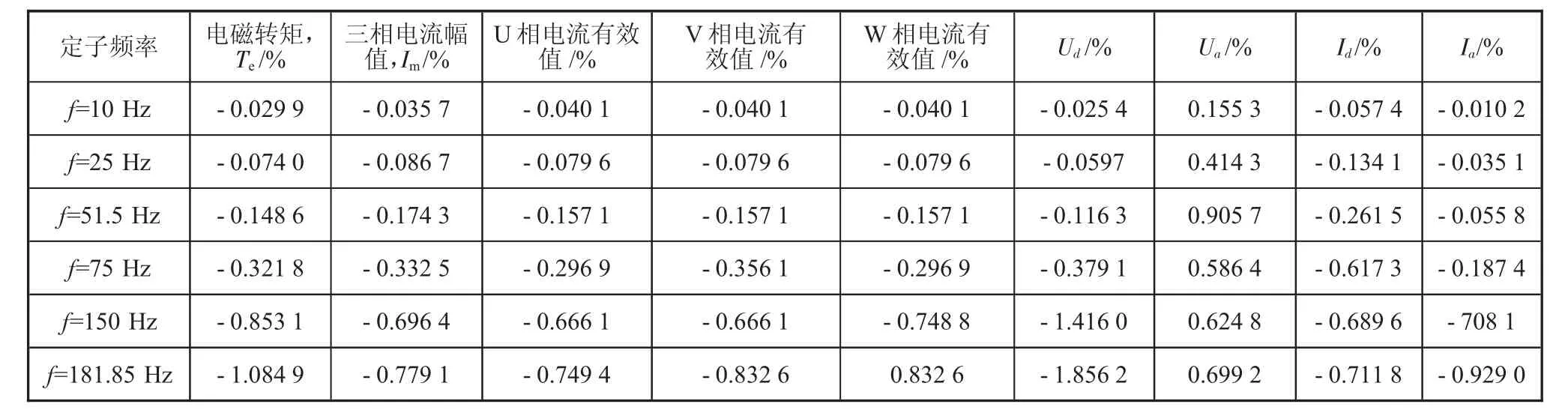
表2 半实物模型与电机电气仿真模型仿真结果误差统计表
在半实物仿真平台上与真实的牵引控制单元(TCU)联调,采样步长为100 ns,完成永磁系统的牵引工况半实物联调试验。牵引系统控制算法为矢量控制,低速下采用异步调制方式,载波比不固定,中高速范围内采用同步调制下的SHE控制方式,当电机转速达到特定值时切换为方波控制。旋转变压器输入输出信号波形如图4所示,牵引系统联调试验波形如图5所示。
图4中为旋转变压器的激励、正弦、余弦输出信号波形,通道说明如表3所示,激励为10 kHz的正弦载波,正弦、余弦信号为旋转变压器副边得到的同相位的正弦信号,两路信号幅值上为空间正交关系,正交频率由电机转速决定。
图5中为5 500 r/min的电机转速下牵引工况联调试验波形,通道说明如表4所示。从逆变输出电压波形可以看出此时为方波控制方式,两相电流局部波形如图6所示,输出的电磁转矩波形如图7所示。

图4 旋变信号波形

表3 图4中波形信号定义
用MATLAB分析得出逆变输出U相、V相电流有效值分别为146.1 A、146.2 A,接近地面试验结果,由于半实物试验环境比地面试验好,谐波含量较低,电流有效值比地面试验结果略低,允许存在一定范围内的误差;半实物试验输出转矩值为1 238 N·m,转矩脉动为264 N·m,转矩脉动较大,控制软件有待进一步优化。
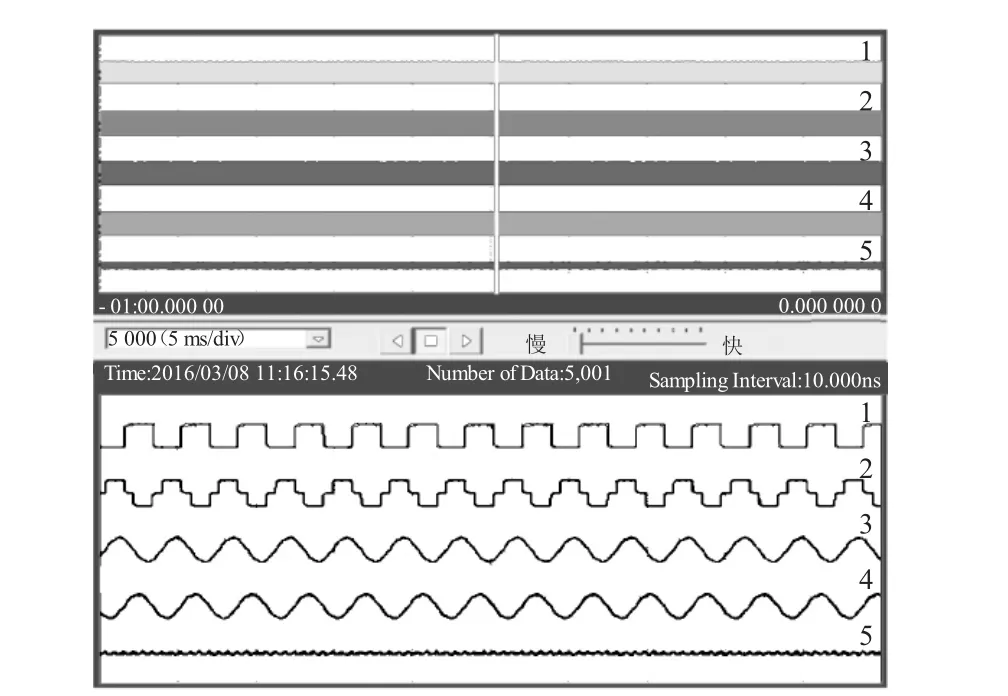
图5 牵引系统仿真试验波形

表4 图5中波形信号定义

图6 逆变输出U、V相电流局部波形
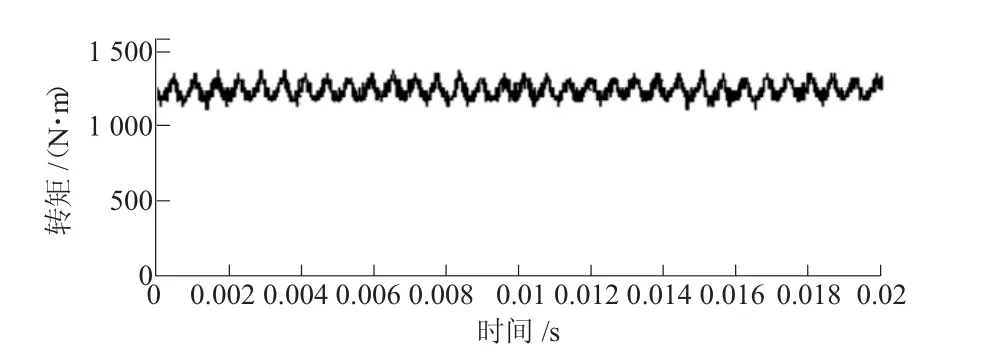
图7 输出电磁转矩局部波形
4 结论
本文基于FPGA搭建永磁同步电机半实物仿真模型,离线情况下永磁同步电机半实物模型与电机电气仿真模型对比,验证模型准确性,与真实的牵引控制系统联调完成牵引工况试验,系统运行稳定,半实物仿真试验结果接近地面试验结果,电机输出的转矩脉动仍较大,半实物仿真结果与实际电机设计数据对比,精度均达到95%以上,满足系统准确性要求,该模型可用于研究和验证以永磁同步电机为牵引电机的控制算法。
[1]王兆安,黄俊.电力电子技术:第4版[M].北京:机械工业出版社,2003.
[2]王坚.电力电子系统硬件在回路仿真技术探讨[J].大功率变流技术,2011(2):1-5;21.
[3]王秀利.电力机车交流传动系统半实物仿真的研究[D].杭州:浙江大学,2005.
[4]刘晨,王秀利,冯江华,等.半实物仿真环境下大功率逆变器建模的补偿算法[J].机车电传动,2005(4):7-9;19.
[5]郭希铮,尤小杰,徐从谦,等.大功率电力牵引控制系统硬件在回路实时仿真[J].电工技术学报,2012,27(4):65-70.
[6]何海兴,王坚.基于dSPACE半实物仿真平台的永磁同步电动机数学模型的实现[J].变流技术与电力牵引,2006(5):40-45.

