顾及共模误差的大区域GPS网坐标时间序列噪声分析

王 健，许安安，周伯烨

(1.武汉大学测绘学院，湖北 武汉 430079； 2.武汉大学GNSS研究中心，湖北 武汉 430079)

全球IGS基准站累积了近20余年的时间序列，为研究人员提供了丰富的数据基础。GPS坐标序列不仅包含构造信号，也包含地表环境负载及未模型化的误差等干扰源，影响GPS解的精度和可靠性。近年来，研究表明连续GPS坐标时间序列中不仅存在白噪声(white noise,WN)，还存在有色噪声，如闪烁噪声(flicker noise,FN)和随机漫步噪声(random walk noise,RWN)等[1]。

Williams等对全球414个GPS站的时间序列进行分析，其最优噪声模型可以通过白噪声+闪烁噪声的组合来描述[2-3]；黄立人等发现GPS噪声时间序列都具有白噪声+闪烁噪声的特点[4-5]；李昭等发现中国区域IGS站噪声模型主要表现为白噪声+闪烁噪声和白噪声+带通幂率噪声[6]；姜卫平分析澳大利亚板块时，发现水平分量最优模型为白噪声+闪烁噪声的组合[7]；相关研究人员对噪声模型进行了进一步分析[8-12]。

然而，GPS时间序列中还包含某种与时空相关的误差，即共模误差(common mode error,CME)。共模误差对GPS时间序列分析有着重要的影响，这种空间域误差则采用数据后处理方法予以削弱，称之为区域时空滤波。国内外学者对共模误差的提取方法进行了研究。Wdowinski等首次提出了堆栈滤波的方法，通过对GPS单日解坐标残差序列进行CME计算，以实现CME的分离[13]；Nikolaidis在Wdowinskiet等的基础上进行了改进，提出了加权堆栈滤波的方法[14]；Dong等采用PCA与KLE相结合的滤波方法进行CME剔除[15]。

主成分分析(PCA)方法能够考虑各站不同的空间特性，是现有剔除共模误差最有效的方法之一。但对长基线GPS网剔除共模误差前后的噪声分析研究相对较少，因此本文使用PCA法对欧洲区域9个 GPS台站2006—2014年的时间序列剔除共模误差，分析滤波前后噪声的变化影响，为后期分析该地区连续GPS站坐标时间序列特性和形变特征提供参考。

1 噪声模型分析方法

1.1 基本原理

分析噪声的方法主要有：最大似然估计(MLE)、频谱估计、经验估计及最小范数二次无偏估计理论等。本文选择CATS软件进行噪声估计，该程序用于研究和比较连续时间序列中的随机噪声过程，并为其参数分配真实的不确定度。

CATS采用的主要方法是最大似然估计法，为估计噪声分量和线性方程的参数，对于给定的一系列观测量x，必须是这些值发生的概率(l)最大。假定一个高斯分布，其似然l为

(1)

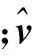
1.2 数据处理策略

本文选取了WN(白噪声)、WN+FN(白噪声+闪烁噪声)、WN+PL(白噪声+幂率噪声)、WN+RWN(白噪声+随机漫步噪声)、WN+RWN+FN(白噪声+随机漫步噪声+闪烁噪声)共5种噪声模型，采用CATS软件对滤波前后噪声进行分析。

1.3 最优噪声模型评价准则

根据极大似然估计原理，不同的噪声模型组合将得到不同的极大似然对数值，数值越大，结果越可靠。然而，噪声模型包含的未知参数越多，其MLE值越大。为了确保结果的可靠性，不能简单地选择MLE值较大的模型作为最优噪声模型。

本文选用Langbein提出的保守估计准则判断不同模型的优劣。先以WN为零假设，然后将WN+FN和WN+RWN模型的MLE值与零假设作比较，如果MLE差值大于2.6则拒绝零假设，否则认为所选模型无效，若两种模型均优于零假设，则选择MLE值较大者作为最优模型。假设此时WN+FN为最优模型，则接受WN+PL或WN+RWN+FN的阈值为2.6。见表1。

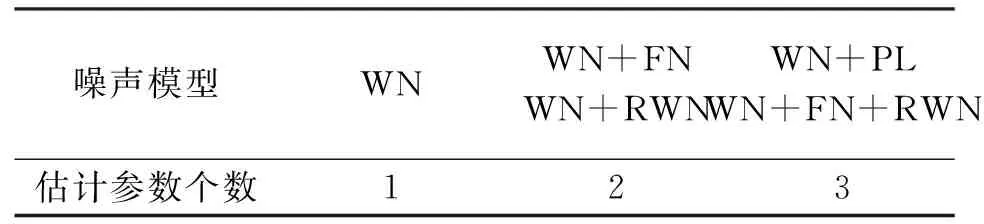
表1 各噪声模型估计参数个数统计

2 数据处理

2.1 GPS时间序列

要准确估计IGS台站坐标时间序列的线性项、周期项及其精度，通常要求时间序列跨度大于2.5年，本文选取了欧洲地区平均基线长度大于2000 km的9个GPS台站2006—2014年的每日观测数据作为处理数据，来源于斯克里普斯轨道和永久性阵列中心(SOPAC)。为了使台站选择更具有实际意义，选择的台站分布中包含了空间特征较为明显的SLOM站、TELA站两个台站。

GPS台站时间序列中包含速度项、阶跃信号、周年和半周年项等非构造信号，相关学者研究表明GPS单站、单分量位置时间序列y(ti)通常满足模型为

y(ti)=a+bti+csin(2πti)+dcos(2πti)+

Tkj)/τj)H(ti-Tkj)+vi

(2)

式中，a为初始位置；b为速率；c、d、e和f分别为年、半年周期项系数；g为阶跃；h为震后速率变化；k为震后速率衰减指数模型；H为阶梯(heaviside step)函数；ti为时间；T为跳变发生的时刻即历元；v为误差。

利用式(2)模型，对GPS台站的3个方向分量时间序列分别拟合处理，采用最小二乘方法求解，剔除粗差，进行插值后重新拟合得到残差时间序列。

2.2 主成分分析滤波

共模误差是区域连续GPS网中存在的一种时空相关的误差。本文选择的主成分分析法(PCA)是一种能够顾及各个台站特征的广义的空间滤波方法，它无需假设共模误差在空间上是均匀分布的，仅通过数学变换的方式提取各个台站各方向的主分量作为共模误差。

采用PCA法得到的第一主成分贡献率分别为41.9%、53.2%、43.9%，第二主成分的贡献率分别为27.2%、19.7%、11.9%，第三主成分的贡献率为9.6%、8.5%、10.3%，而第四主成分的贡献率仅为5.3%、3.9%、7.4%。前3个主成分累计贡献率为78.8%、81.4%、66.2%，如图1所示，前3个主成分的贡献率综合了大部分的有用信息，图2显示了前3个主成分的空间响应，因此本文PCA采用这3个主成分的和作为区域的共模误差。

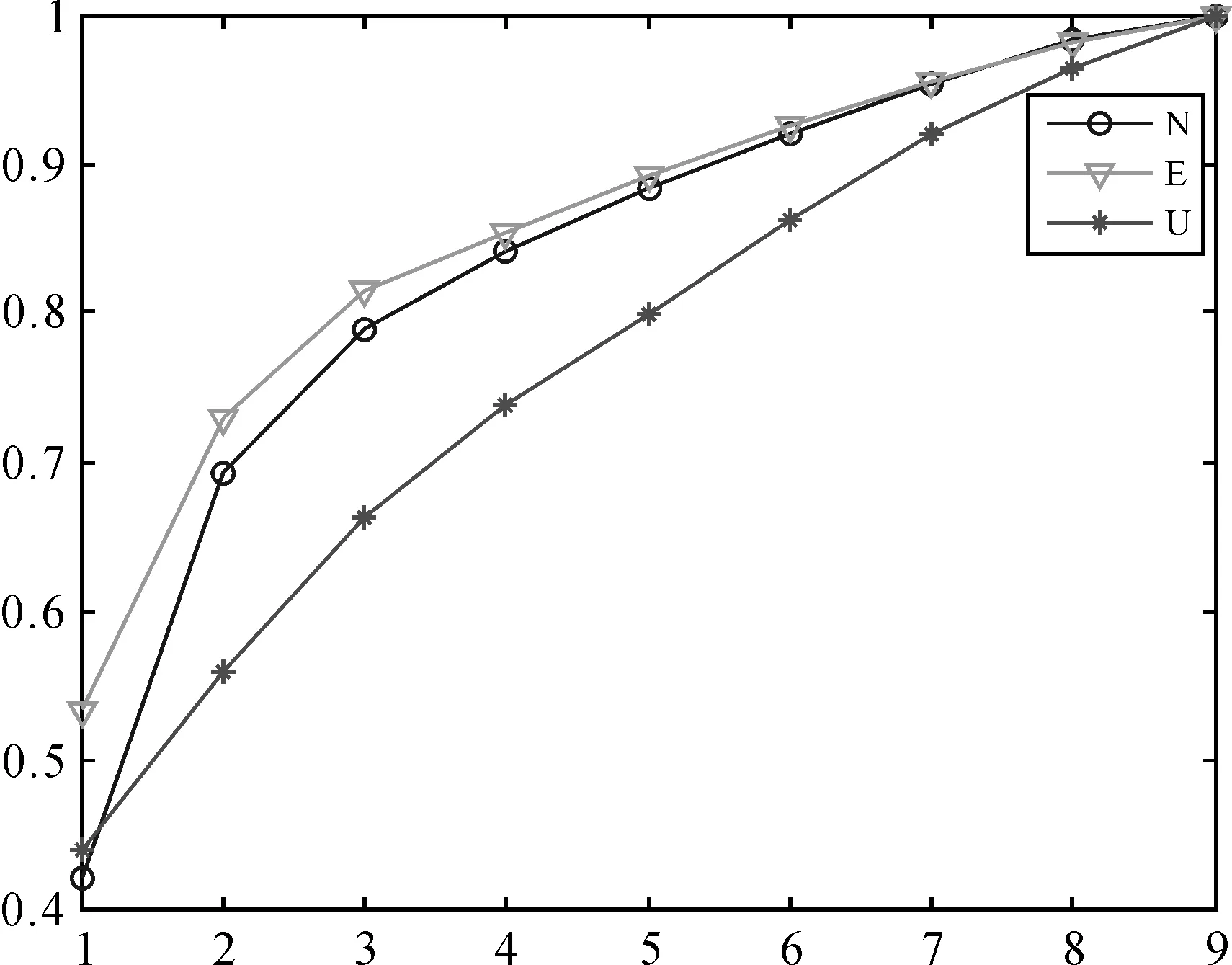
图1 各方向累加贡献率

主成分分析滤波前后均方根的比较见表2。

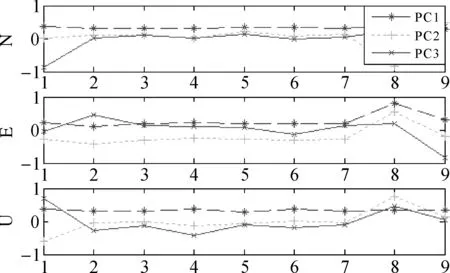
图2 空间响应

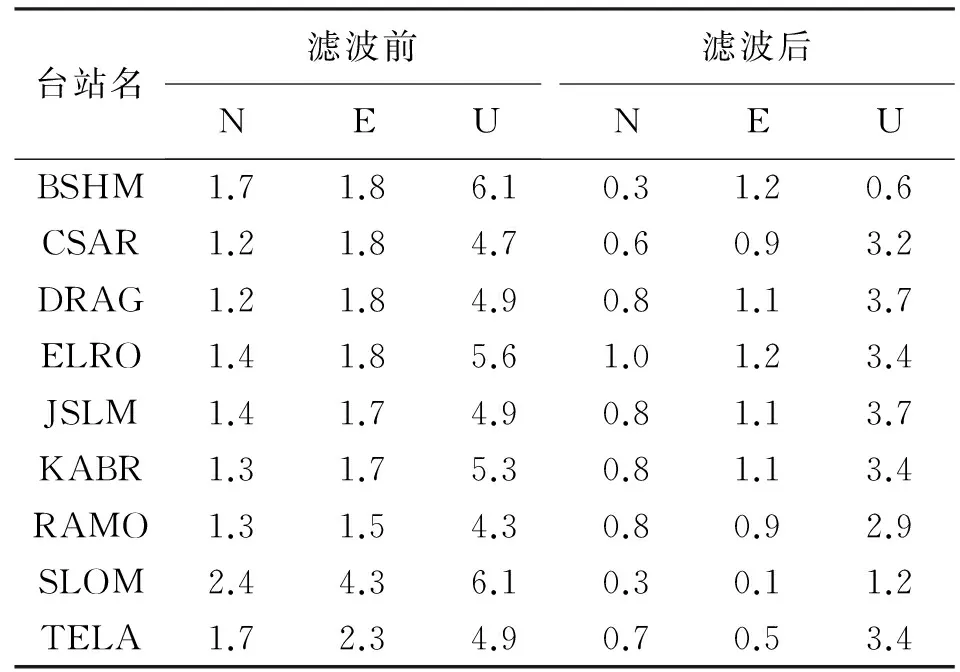
mm

3 GPS坐标时间序列最优噪声模型

3.1 滤波前后时间序列谱指数

利用CATS软件对共模误差剔除前后的时间序列进行分析，求得滤波前后时间序列的谱指数，见表3。

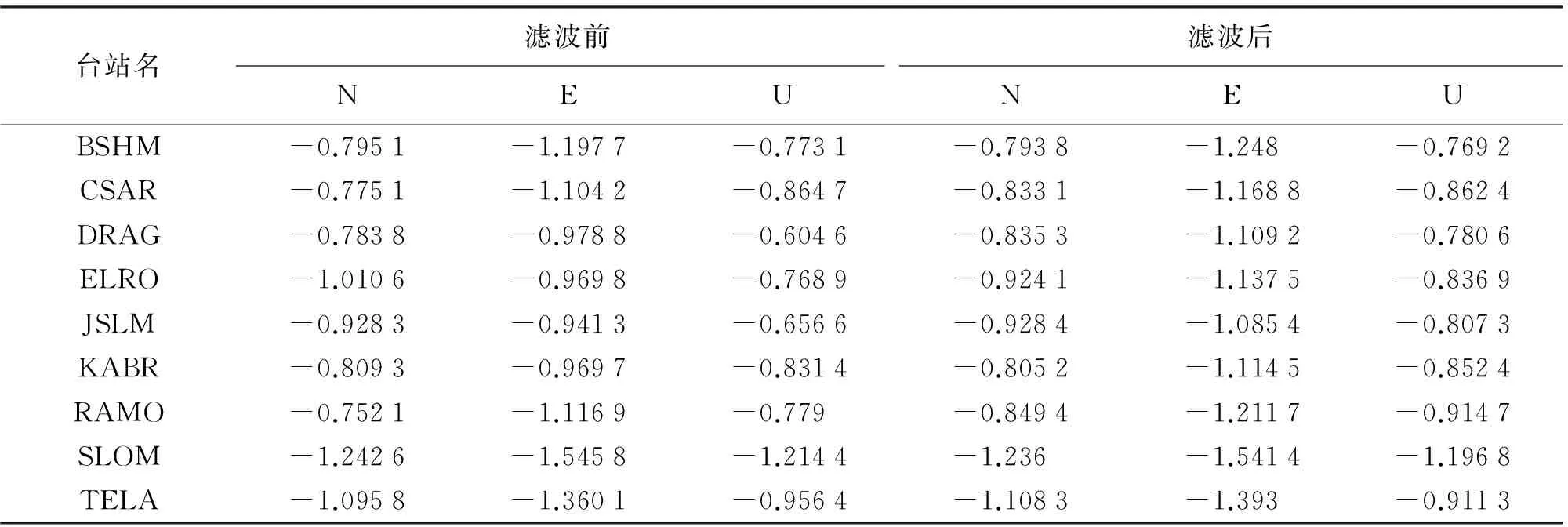
表3 滤波前后谱指数

由表3可以得到，当滤波前谱指数<-1时，谱指数增大比例为66.7%；当滤波前谱指数>-1时，谱指数减小比例为61.1%。

3.2 滤波前后时间序列最优噪声模型建立

通过MLE值来确定滤波前后最优噪声模型，加粗的即为最优噪声模型发生改变，统计结果见表4。

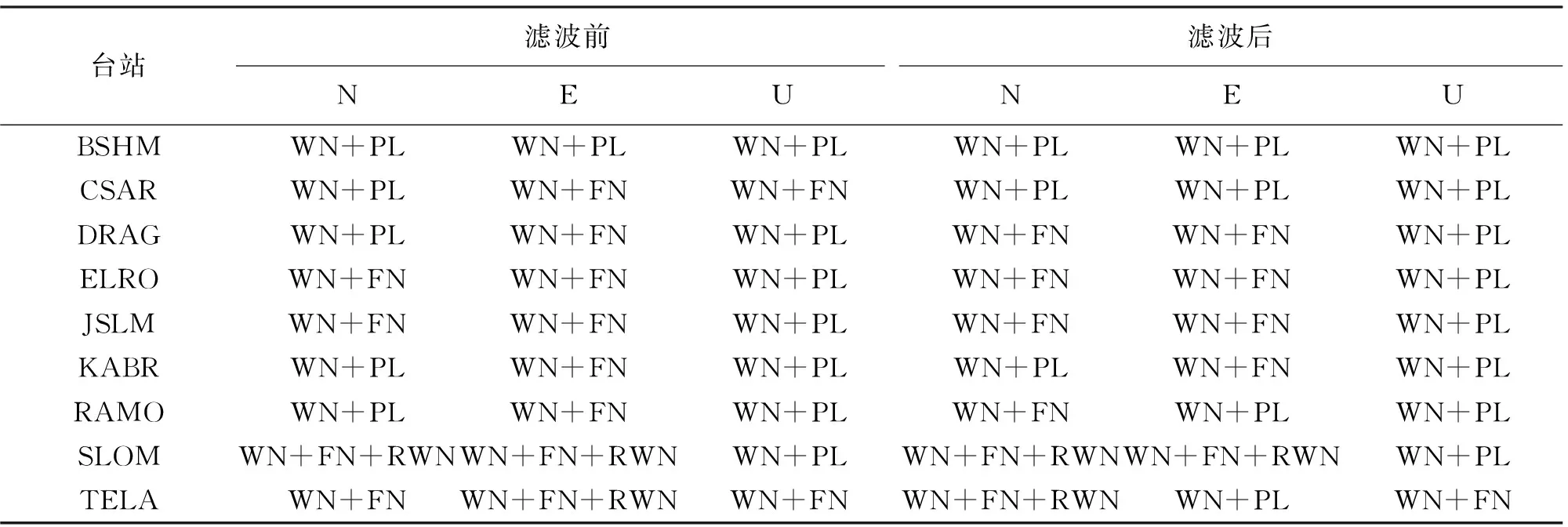
表4 滤波前后最优噪声模型

通过表4可以得到，除个别台站(如SLOM、TELA)N、E方向外，滤波前后最优噪声模型仍以WN+FN、WN+PL为主。

3.3 滤波前后速度场变化

根据最优噪声模型可以提取对应的速度场。对滤波前后的速度场求差，可得到空间滤波对速度场的影响，对速度场变化量进行统计，如图3所示。

图3 滤波前后速度场变化量

通过统计可以得到，除SLOM站、TELA站外，N、E方向速度场变化为0.2 mm/a，U方向速度场改变量的平均值为-0.5 mm/a。

4 结 论

本文通过对欧洲区域9个长基线的IGS站9年时间序列进行分析，得到GPS台站坐标时间序列最优噪声模型以WN+FN、WN+PL为主，其中，空间特征明显的SLOM、TELA台站N、E方向还含有RWN噪声。

GPS时间序列经过剔除共模误差后，最优噪声模型发生部分改变，但仍以WN+FN、WN+PL为主，谱指数也发生相应改变，滤波对坐标速度场也产生了重要影响，N、E方向速度场变化为0.2 mm/a，U方向速度场变化量级为0.5 mm/a。因此，大区域GPS网中，共模误差的剔除对噪声分析及确定更加准确的速度场有着重要影响。

参考文献：

[1] MAO A，HARRISON C G A，DIXON T H.Noise in GPS Coordinate Time Series[J].Journal of Geophysical Research Atmospheres，1999，104(B2):2797-2816.

[2] WILLIAMS S D P，BOCK Y，FANG P，et al.Error Analysis of Continuous GPS Position Time Series[J].Journal of Geophysical Research Solid Earth，2004，109(B3):3412-3421.

[3] WILLIAMS S D P.CATS: GPS Coordinate Time Series Analysis Software[J].GPS Solutions,2008，12 (2)：147-153.

[4] 黄立人.GPS基准站坐标分量时间序列的噪声特性分析[J].大地测量与地球动力学,2006(2):31-33.

[5] 黄立人,符养.GPS连续观测站的噪声分析[J].地震学报2007,29(2):197-202.

[6] 李昭,姜卫平,刘鸿飞,等.中国区域IGS基准站坐标时间序列噪声模型建立与分析[J].测绘学报,2012,41(4):496-503.

[7] 姜卫平,周晓慧.澳大利亚GPS坐标时间序列跨度对噪声模型建立的影响分析[J].中国科学(地球科学),2014(11):2461-2478.

[8] 杨国华,张风霜,武艳强,等.GPS基准站坐标分量噪声的时间序列与分类特征[J].国际地震动态,2007(7):80-86.

[9] 杨登科,邓连生,安向东,等.IGS基准站坐标时间序列最优噪声模型变化探讨[J].测绘地理信息,2016(1):7-10.

[10] 李斐,马超,张胜凯,等.南极半岛地区GPS坐标时间序列噪声分析及形变模式初探[J].地球物理学报,2016,59(7):2402-2412.

[11] 贺小星.GPS坐标序列噪声模型估计方法研究[J].测绘学报，2017,46(3):398.

[12] 杨晶,顾慧,王勇,等.基于EMD的GPS对流层延迟变化分析[J].测绘通报,2016(6):55-59.

[13] WDOWINSKI S，BOCK Y，ZHANG J, et al. Southern California Permanent GPS Geodetic Array:Spatial Filtering of Daily Positions for Estimating Coseismic and Postseismic Displacements Induced by the 1992 Landers Earthquake[J].Journal of Geophysical Research，1997，102:18057-18070.

[14] NIKOLAIDIS R.Obser Vation of Geodetic and Seismic Deformat Ion with the Global Positioning System[D].San Diego:University of California,2002.

[15] DONG D,FANG P，BOCK Y,et al.Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Love Expansion Approaches for Regional GPS Network Analysis[J].Journal of Geophysical Research:Solid Earth(1978—2012),2006，111(B3):405-421.