高超声速飞行器模型弹性特性影响的机理分析

张希彬，张振兴

(天津科技大学理学院，天津 300457)

高超声速飞行器具有强突防、强摧毁、快速反应及精准打击的能力，能够在大气层边缘临近空间飞行，1～2,h内到达全球任何地方．近年来，美国、俄罗斯、中国、印度等国家均投入大量财力研究高超声速飞行器，其中美国的成绩最为突出，从20世纪90年代至今，试飞了一系列构型的飞行器，比较有代表性的是X-43A和X-51系列构型飞行器．其中，X-43A验证机在第3次试飞中上升到33.5,km高空，马赫数达到了 9.65，刷新了大气层内飞行速度记录．作为X-43A构型的延续，X-51构型已进行 5次试飞．对此类高超声速飞行器的研究，是近年来空天飞行器领域的研究热点[1-2]．

高超声速飞行器的飞行速度一般高于5倍音速，采用轻质材料、细长体结构．在高速飞行环境下，飞行器机身极易发生弹性形变，产生弹性效应与气动布局、推进系统之间的强耦合性，给飞行器建模与控制带来挑战．Chavez等[3]针对 X-30飞行器构型，采用牛顿碰撞理论分析弹性飞行器受力，利用NASTRAN有限元法估算弹性模态，建立了弹性飞行器动态解析模型．随着美国X-43A的试飞成功，Bolender等[4]基于 X-43A飞行器构型，采用激波膨胀波理论和活塞理论计算弹性飞行器受力，利用梁的振动理论和假设模态法计算弹性模态，采用拉格朗日方程建立了复杂的弹性高超声速飞行器动力学机理模型．其后，又在模型受力分析中加入了弹性非定常效应及黏性效应[5-6]．Clark等[7]基于 X-43A飞行器构型，主要采用CFD技术和 NASTRAN有限元法，分析弹性飞行器受力及估算弹性模态．Fredreis等[8]基于一类弹性高超声速飞行器构型，采用激波膨胀波理论和泰勒麦克方程计算飞行器受力，结合 CFD技术，考虑弹性结构梁的振动，建立了高超声速飞行器六自由度模型．Khatri[9]基于机理分析方法研究了一类飞行器的气动-热-推进-弹性结构之间的耦合问题．Praneeth等[10]利用里茨法计算弹性模态和频率，讨论了高超声速飞行器的结构弹性问题．李慧峰等[11]基于拉格朗日方程法，建立了高超声速飞行器刚体/弹性体耦合的动力学模型．Zong等[12]和 Zeng等[13]分别采用机理分析方法，分析了一类弹性高超声速飞行器的气动伺服弹性影响．Zhang等[14]将飞行器机身看作两个悬臂梁结构，采用牛顿碰撞理论计算机身表面受力，分析了吸气式高超声速飞行器刚体和弹性的耦合影响．

如何建立真实描述飞行环境与特性的模型是飞行器建模与控制的关键．弹性效应对气动及推进系统的耦合影响在建模中不容忽视．相对于牛顿碰撞理论与激波膨胀波理论，活塞理论在飞行器气动的计算中能够加入弹性定常与非定常效应，更接近真实气动的物理特性．本文针对高超声速飞行器纵向几何构型，基于带有强耦合项的飞行器动力学模型，采用活塞理论方法，从机理上分析飞行器弹性形变及其对气动布局和推进系统的影响，对弹性效应与气动、推进系统之间的强耦合性进行仿真分析，为控制器设计提供模型分析基础．

1 高超声速飞行器动力学模型

高超声速飞行器的纵向几何构型如图1所示，采用机身-发动机一体化结构设计，发动机为超燃冲压发动机，位于机身下腹部．为了吸入更多的空气质量流，在发动机进气道口处安有可移动的罩门．控制面主要有位于前体的鸭翼面和位于后体的升降舵面．

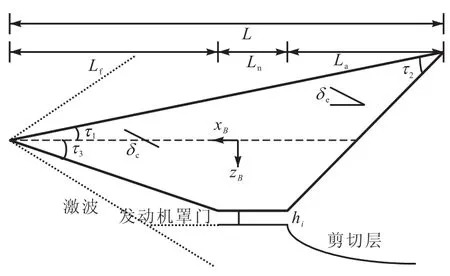
图1 高超声速飞行器纵向几何构型Fig. 1 Hypersonic air vehicle geometry

高超声速飞行器机身的细长体结构一般可看作两端自由梁．在高速飞行中，飞行器前体产生斜激波或膨胀波，气动和气动加热的作用使得飞行器机身极易发生弹性形变，产生前体和后体变形角Δ1τ和Δ2τ，如图 2所示．随着机身发生弹性形变，飞行器表面的流场特性和质心位置也将发生改变，从而影响整个飞行器的气动布局和发动机推进系统性能．而气动特性的改变又将加剧飞行器机身的弹性形变，产生弹性形变与机身表面气动、发动机推进系统之间的耦合性．

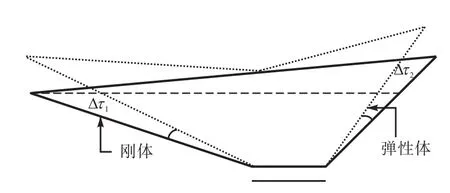
图2 高超声速飞行器弹性结构图Fig. 2 Flexible hypersonic air vehicle geometry

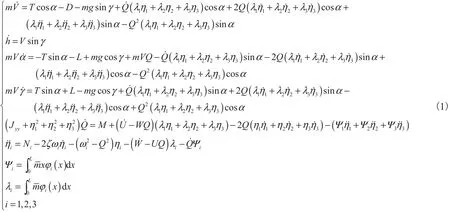
在速度坐标系下，采用拉格朗日方程法，可建立飞行器纵向一体化动力学模型[4-5]式中：刚体状态分别为速度、高度、攻角、航迹角和俯仰角；弹性体状态为描述弹性体振动的广义坐标及其对时间的导数；分别为弹性结构阻尼比、固有频率、弹性模态和广义力；分别为转动惯量、飞行器质量、质量分布和重力加速度；分别为飞行器升力、阻力、推力及俯仰力矩；分别为飞行速度沿机体轴的分量；x, z为飞行器在机体轴上的位移为惯性耦合项，能够描述刚体和弹性体之间的耦合性．此外，刚体和弹性体模态的耦合特性及控制输入量：升降舵偏转角δe、鸭翼偏转角δc和发动机油门开度φ还体现在升力、阻力、俯仰力矩、推力和广义力的表达式中．刚体和弹性体模态的强耦合性使得飞行器动力学模型复杂，难以进行控制器设计．

2 弹性特性机理分析

2.1 弹性特性对气动的影响

高超声速飞行器各表面纵向受力如图 3所示．飞行器的受力区域主要包括机体上表面、前后体下表面、升降舵上下表面、鸭翼上下表面及发动机下表面．

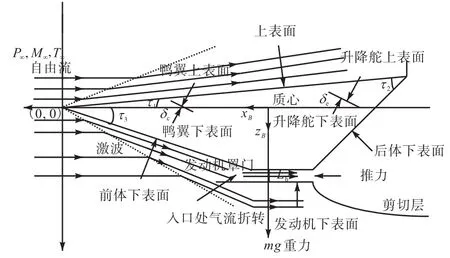
图3 飞行器表面受力图Fig. 3 Forces acting on the air vehicle surface

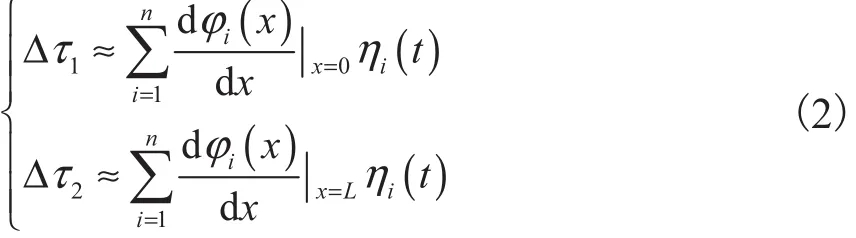
式中：为弹性模态，可由 CFD或假设模态法计算得到；为弹性状态；L为机身长度．

飞行器机身结构发生弹性形变，机身表面的气流斜激波或膨胀波特性将发生改变，从而改变作用在飞行器表面的气动力．

对于飞行器机身，以上表面为例，当攻角时，产生斜激波；当攻角时，产生膨胀波；当时，流经上表面的流体为自由流．

考虑机身弹性模态与气动之间的耦合影响，采用活塞理论计算弹性飞行器表面受力．一阶活塞理论力的微元表达式为

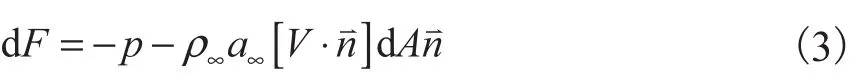
加入弹性效应影响，机身上表面气流流速为

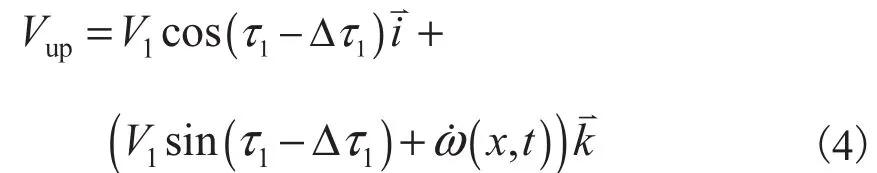
式中：V1为激波或膨胀波后气流速度；为机体坐标系xB方向的单位向量；为机体坐标系zB方向的单位向量．

将流速代入一阶活塞理论公式(3)，积分可得到作用在机身上表面的作用力和力矩为

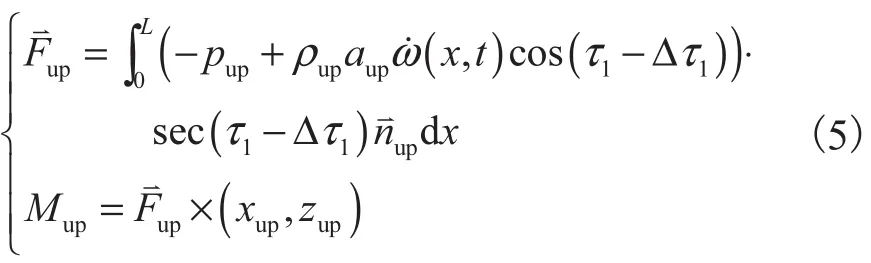
对于前体下表面，采用活塞理论类似可得作用力和力矩为

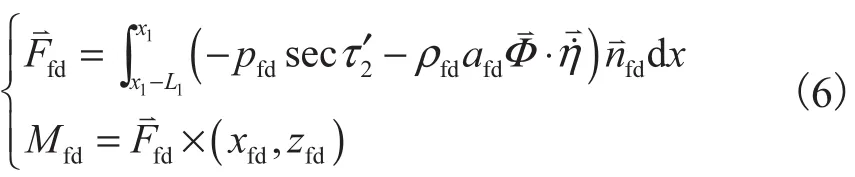
对于后体下表面，采用活塞理论可得作用力和力矩为

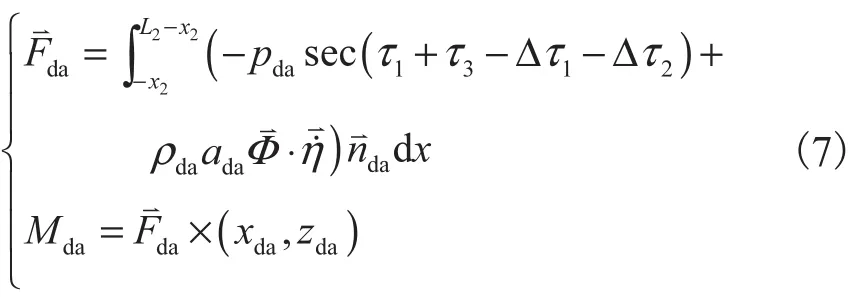
式中：pda、ρda、ada为机身后体下表面气流压强、密度和声速；单位法向量；x2为后体端点到质心的距为后体下表面相对质心的受力中心点．

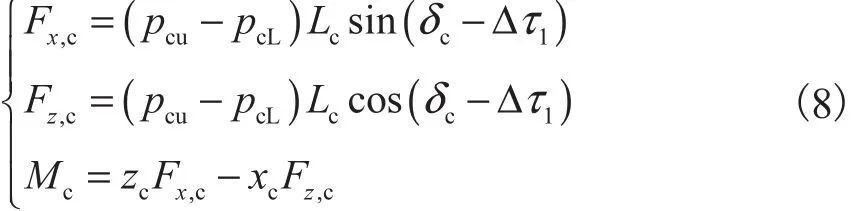
式中：pcu、pcL分别为鸭翼面上下表面的压强；Lc为鸭翼长度；为鸭翼面受力中心．

飞行器升降舵面受力及力矩与鸭翼面类似求得．从而可得到作用在飞行器机身的力和力矩在机体轴上的分量．利用坐标变换，得到作用在飞行器表面的升力、阻力和俯仰力矩．可以看出，受力表达式中因加入了弹性效应，体现弹性模态和气动之间的耦合性，使得飞行器气动模型更加复杂[15]．

2.2 弹性特性对飞行器发动机性能的影响

高超声速飞行器的超燃冲压发动机结构如图 4所示，由进气道、燃烧室和内喷嘴3部分构成．

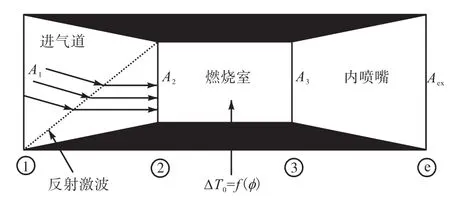
图4 超燃冲压发动机结构图Fig. 4 Scamjet cross section

发动机一般为刚体结构，前体下表面的气流特性决定着发动机进气道口流体特性．当机身发生弹性形变时，前体下表面流场的改变将直接影响发动机的工作状态．

采用准一维可压缩流理论计算推力表达式为[4]

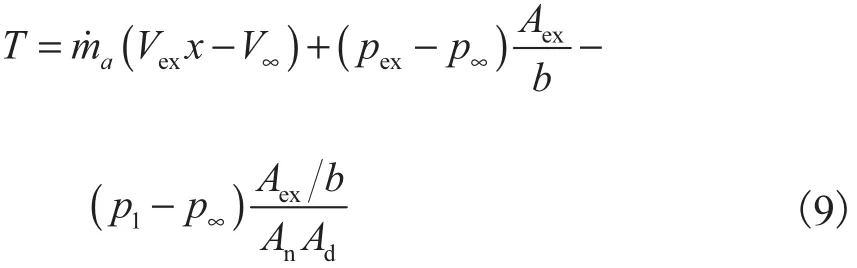
为避免进入发动机的流体溢出而损失推力，达到发动机工作的最好性能，假设激波与发动机可移动罩门口处相交，此时空气质量流速[4]

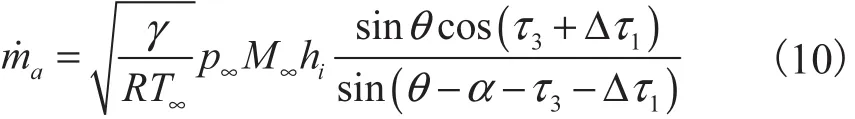
推力产生的俯仰力矩为

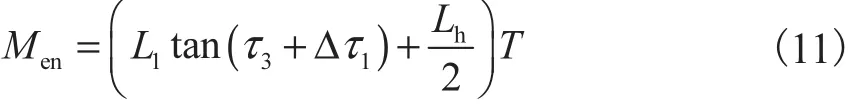
空气质量流速、推力及推力产生的俯仰力矩表达式中包含来流特性、攻角及弹性效应，机身的弹性形变和流场的改变直接影响推力系统的变化，体现弹性效应与气动和发动机推进系统的耦合．

3 仿真分析

3.1 弹性模态分析

将机身看作两端自由梁结构，其前三阶弹性振型函数和振型函数的导数如图 5所示．将自由梁结构的弹性振型函数作为假设模态，采用假设模态法，能够获取弹性高超声速飞行器的弹性频率，前三阶弹性频率分别为 19.743,7,rad/s、47.785,1,rad/s、94.820,3 rad/s．考虑前三阶弹性模态，式(1)中的惯性耦合系数可求解如下：

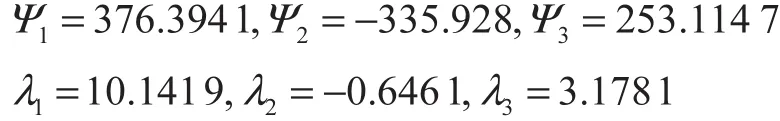
在实际中，机身表面的气动加热等使得飞行器弹性频率降低，使得第一阶弹性频率与刚体频率接近，容易发生刚体与弹性模态之间的耦合．在弹性体建模中，一般只考虑较低阶弹性模态．

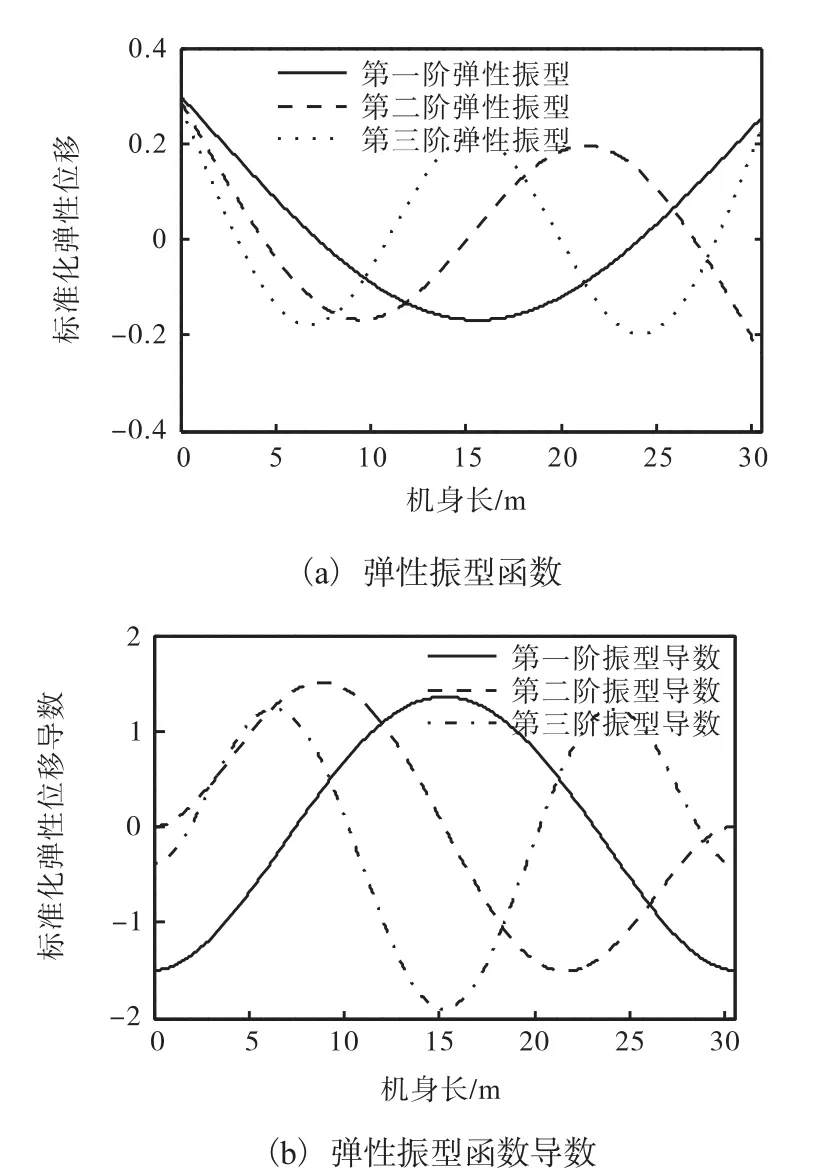
图5 弹性振型函数及导数图Fig. 5 Flexible mode shapes and mode shape derivatives

3.2 弹性形变对气动的影响分析

利用机理分析得到的飞行器升力、阻力、俯仰力矩和广义力一般为飞行马赫数Ma、攻角α、升降舵偏转角eδ、鸭翼面偏转角cδ及前后体变形角的函数，即

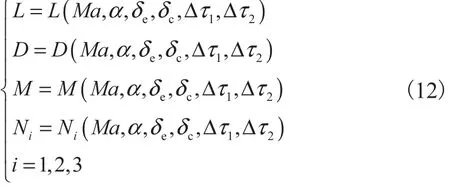
在一定气动条件下，基于由机理分析获取的飞行器气动数据，分析当飞行器机身发生弹性形变时，作用在飞行器表面的升力、阻力、俯仰力矩和广义力的变化规律，研究弹性形变对气动的耦合影响．

图6分别为升力、阻力和俯仰力矩随飞行器前体和后体变形角的变化图，可以看出：升力随前体变形角的增大而增大，随后体变形角的变大有减小的趋势．阻力随前体变形角的增大先减小后增大，与前体变形角呈现二次函数关系，随后体变形角的增大而减小．俯仰力矩随前体和后体变形角的增大均有增大的趋势．这是因为飞行器机身的弹性振动形变导致了飞行器表面流场发生改变，影响了机身表面受力．

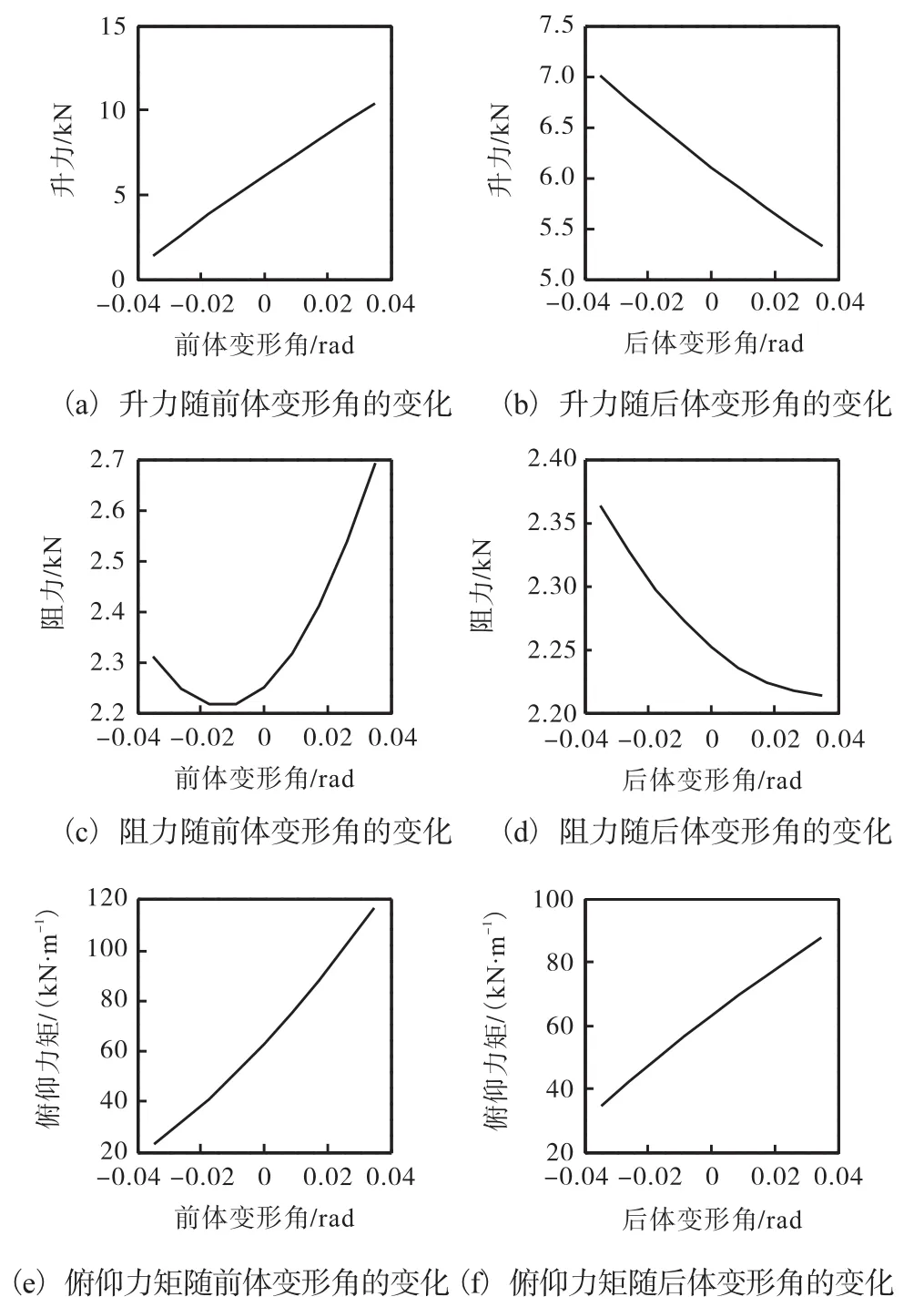
图6 力和力矩随变形角的变化Fig. 6 Force and moment of the deformation angle

图 7为刚体飞行器和加入弹性效应后飞行器的气动数据比较图．

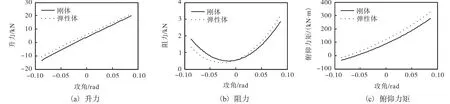
图7 力和力矩的趋势图Fig. 7 Trend of the force and moment

由图 7可以看出，升力、阻力和俯仰力矩随攻角变化的趋势没有改变，加入弹性效应后，飞行器受力均有不同程度的增大或减小．在建模中，弹性效应不容忽视．而升力、阻力和俯仰力矩表达式中包含的弹性模态，这也使得飞行器气动模型和动力学模型更加复杂．

3.3 弹性形变对发动机的影响分析

由式(9)可以看出：发动机推力为飞行马赫数Ma、攻角α、油门开度φ及前体变形角Δ1τ的非线性函数．在一定气动条件下，基于机理分析所获取的飞行器气动及发动机数据，可以分析当飞行器机身发生弹性形变时，发动机内部气动及推力的变化规律，研究弹性形变对发动机系统的影响．

图 8为发动机燃烧室温度增量在刚体和考虑弹性效应时的变化趋势图，可以看出，弹性效应的加入使得燃烧室温度增量升高．在实际中，若燃烧室温度增量超过一定临界值，空气质量流速减小，使得发动机不能正常工作，即为发动机热壅塞现象．此时需要降低发动机油门开度，以减小推力．

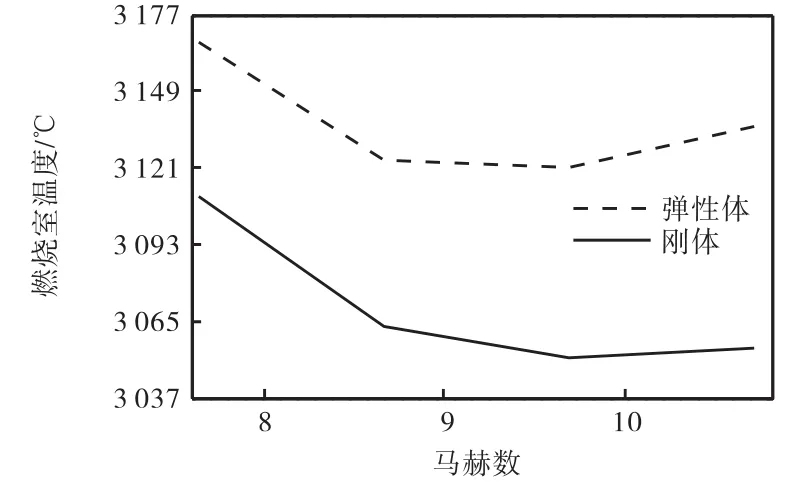
图8 燃烧室温度趋势Fig. 8 Trend of the combustion temperature

图 9为刚体和加入弹性效应后的推力和推力产生的俯仰力矩比较图，可以看出，加入弹性效应后，推力和推力俯仰力矩有减小的趋势．这是由于机身前体的变形导致进入发动机内部的气流特性改变，影响了发动机推进系统．

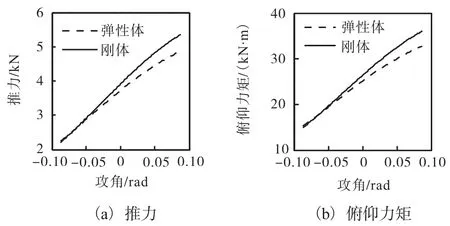
图9 推力及其产生的俯仰力矩趋势图Fig. 9 Trend of the thrust and pitching moment

3.4 动态特性分析

高速飞行的飞行器由于机身的弹性形变和飞行中的制动动作能够激励低阶弹性模态，产生刚体和弹性体的耦合，引起机身结构损坏或飞行器失稳．弹性模态随着飞行器几何构型、重心位置、载荷、飞行任务和气动加热等的变化而改变，从而能够产生高超声速飞行器模型的不确定性．

对高超声速飞行器模型在飞行速度8马赫，高度85,000,ft(25,908,m)下线性化，模型输入为升降舵偏转角、鸭翼偏转角和油门开度，输出为攻角和速度．图 10为包含弹性效应的飞行器模型零极点图．可以看出，右半平面存在一个极点，为不稳定的短周期模态，说明模型是不稳定的．特征值中还包含了3对共轭负根，为3个气动弹性模态．右半平面存在零点，与弹性模态一同出现，能够限制控制系统的频率带宽，产生非最小相位现象．

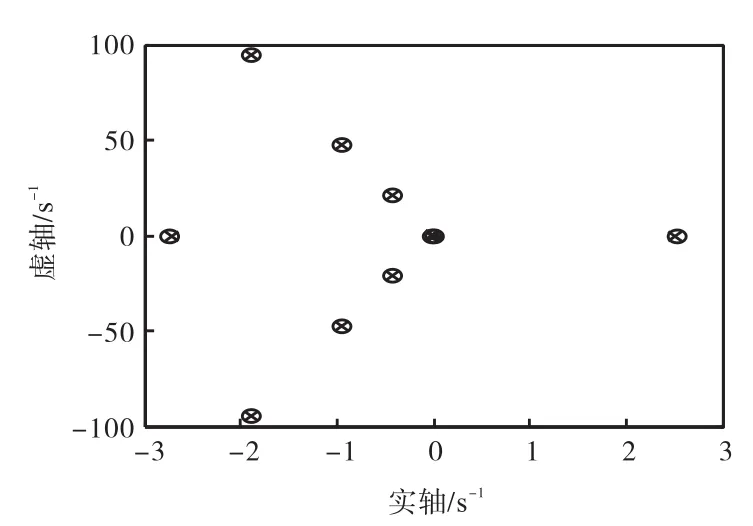
图10 零极点图Fig. 10 The pole-zero map

为了分析弹性效应对飞行器动态特性的影响，图11—图13主要给出了3个控制量对高度和航迹角的波特图．图 11为在开环状态下基于高超声速飞行器动力学模型的发动机油门开度通道对高度和航迹角的波特图，可以看出，飞行器模型中考虑机身弹性形变，弹性模态造成波特图中的低阶频率点处出现尖峰，体现飞行器机身、发动机系统与弹性结构之间的耦合影响．图 12和图 13分别为在开环状态下基于高超声速飞行器动力学模型的升降舵偏转角通道及鸭翼面偏转角通道对高度和航迹角的波特图，可以看出，弹性模态的加入也造成波特图中的低阶频率点处出现尖峰，这体现了飞行器刚体与弹性结构之间的耦合影响．

从各波特图中可以看出，在低阶频率点处尖峰突出，说明低阶弹性模态对飞行器模型的影响起主导作用．

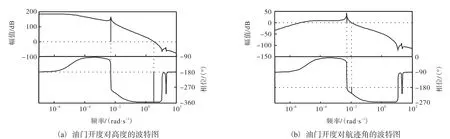
图11 油门开度对高度和航迹角的波特图Fig. 11 Bode graph of the throttle on the altitude and flight path angle

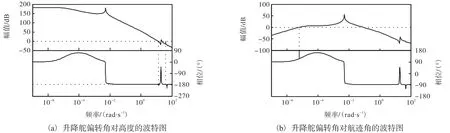
图12 升降舵偏转角对高度和航迹角的波特图Fig. 12 Bode graph of the elevator deflection on the altitude and flight path angle

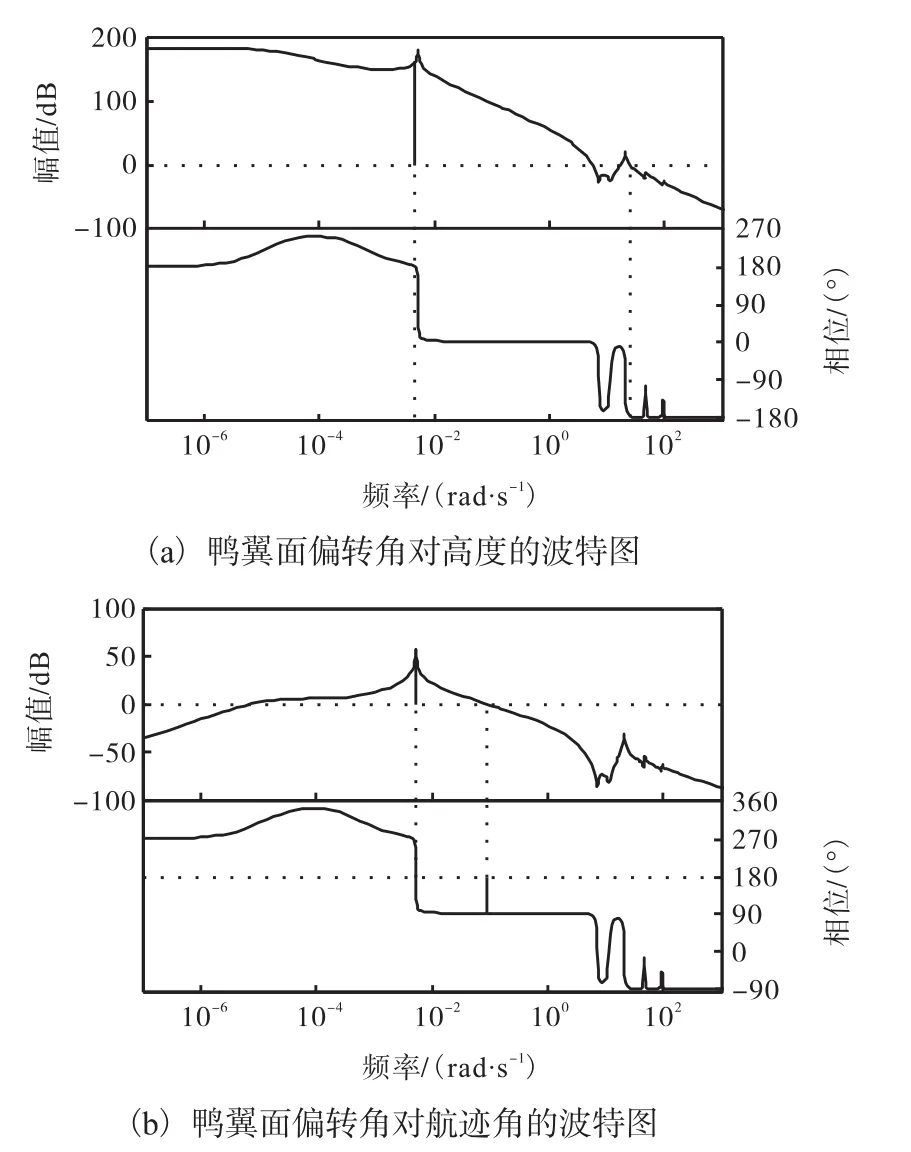
图13 鸭翼面偏转角对高度和航迹角的波特图Fig. 13 Bode graph of the canard deflection on the altitude and flight path angle

飞行器机身弹性形变引起的弹性模态导致刚体和弹性结构之间耦合，产生模型不确定，也在控制系统中产生气动伺服弹性效应影响，造成飞行器控制性能下降甚至失稳．此时可以设计模态抑制和控制闭环回路，抑制由于机身弹性形变产生的弹性模态，实现飞行器系统的稳定性[16-17]．

4 结 语

高超声速飞行器的弹性效应对气动及推进系统的耦合影响给飞行器建模带来挑战．本文基于带有惯性耦合项的飞行器动力学模型，采用机理分析方法，利用活塞理论，计算飞行器机身和控制面发生弹性形变后的气动布局，分析机身发生弹性形变后发动机推进系统的推力，研究了弹性效应对气动及推进系统的影响．基于机理分析获取的气动数据，通过仿真分析表明：低阶弹性模态对飞行器的影响起主导作用．当飞行器机身发生弹性形变时，升力、阻力、俯仰力矩及推力变化显著．通过零极点分析和各通道波特图可知，带有惯性耦合项的飞行器动力学模型复杂，具有强非线性和强耦合性，模型是不稳定的，需设计闭环控制器系统．

参考文献：

［1］ Marshall L A，Corpening G P，Sherrill R. A chief engi-neer’s view of the NASA X-43A scramjet flight test[C]//Proceedings of the 13th AIAA/CIRA International Space Planes and Hypersonic Systems and Technologies Conference. Reston，VA：AIAA，2005：1181-1200.

［2］ Voland R T，Huebner L D，McClinton C R. X-43A Hypersonic vehicle technology development[J]. Acta Astronautica，2006，59：181-191.

［3］ Chavez F R，Schmidt D K. Analytical aeropropulsive aeroelastic hypersonic vehicle model with dynamic analysis[J]. AIAA Journal of Guidance，Control，and Dynamics，1994，17(6)：1308-1319.

［4］ Bolender M A，Doman D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J]. Journal of Spacecraft and Rockets，2007，44(2)：374-387.

［5］ Oppenheimer M W，Doman D B，Bolender M A，et al.Flexible hypersonic vehicle model developed with piston theory[C]//Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit. Reston，VA：AIAA，2007：396-420.

［6］ Oppenheime M W，Doman D B，McNamara J J，et al.Viscous effects for a hypersonic vehicle model[C]//Proceeding of AIAA Atmospheric Flight Mechanics Conference and Exhibit. Reston，VA：AIAA，2008.https：//doi.org/10.2514/6.2008-6382.

［7］ Clark A D，Wu C，Mirmirani M D，et al. Development of an airframe-propulsion integrated generic hypersonic vehicle model[C]//Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit. Reston，VA：AIAA，2006：2625-2654.

［8］ Frendreis S G V，Cesnik C E S. 3D simulation of flexible hypersonic vehicles[C]//Proceeding of AIAA Atmospheric Flight Mechanics Conference. Reston，VA：AIAA，2010. https：//doi.org/10.2514/6.2010-8229.

［9］ Khatri J. Modeling，Analysis，and Control of a Hypersonic Vehicle with Significant Aero-Thermo-Elastic-Propulsion Interactions：Elastic，Thermal and Mass Uncertainty[D]. USA：Arizona state university，2011.

［10］ Praneeth R S，Cornel S，Rakesh K K，et al. Accurate computing of higher vibration modes of thin flexible structures[J]. AIAA Journal，2016，54(5)：1704-1718.

［11］ 李惠峰，肖进，张冉. 高超声速飞行器刚体/弹性体耦合动力学建模[J]. 北京航空航天大学学报，2012，38(2)：160-165.

［12］ Zong Q，You Mg，Zeng F L，et al. Aeroservoelastic modeling and analysis of a six-DOF hypersonic flight vehicle[J]. Proceedings of the Institution of Mechanical Engineers Part G：Journal of Aerospace Engineering，2016，230(7)：1240-1251.

［13］ Zeng K C，Xiang J W，Li D C. Aeroservoelastic modeling and analysis of a canard-configured air-breathing hypersonic vehicles[J]. Chinese Journal of Aeronautics，2013，26(4)：831-840.

［14］ Zhang D，Tang S，Zhu Q J，et al. Analysis of dynamic characteristics of the rigid body/elastic body coupling of air-breathing hypersonic vehicles[J]. Aerospace Science and Technology，2016，48：328-341.

［15］ 张希彬，宗群. 考虑气动-推进-弹性耦合的高超声速飞行器面向控制建模与分析[J]. 宇航学报，2014，35(5)：528-536.

［16］ Levin J，Ioannou P A，Mirmirani M D. Adaptive mode suppression scheme for an aeroelastic airbreathing hypersonic cruise vehicle[C]//Proceedings of AIAA Guidance，Navigation and Control Conference and Exhibit. Reston，VA：AIAA，2008. https：//doi.org/10. 2514/6.2008-7137.

［17］ 张超凡，宗群，董琦，等. 高超声速飞行器模型及控制若干问题综述[J]. 信息与控制，2017，46(1)：90-102.