基于尺度时间均衡的高速风洞视频测量图像闪烁修正方法

范金磊, 张征宇, 黄叙辉

(中国空气动力研究与发展中心 高速空气动力研究所, 四川 绵阳 621000)

0 引 言

图像闪烁是指图像序列的亮度(灰度值)在空间上和时间上非自然的快速变化，这种变化并不是场景中的原始亮度变化的反映。图像闪烁的现象广泛存在，在旧胶片电影修复、视频监控、全景图像拼接和延时摄影等领域都会遇到。尤其是在医学/生物学图像分析、视频/摄影测量和机器视觉等领域，许多分析算法都对亮度敏感，图像闪烁问题会影响结果的精准度。

针对不同的图像，导致其闪烁的主要原因也不同，旧电影中的闪烁是由于早期的电影技术造成的，如胶片成分的退化、曝光不稳定等；而现代视频或影像的闪烁则主要是受摄像机的性能和光照条件变化的影响，如在日光灯照明下采用较短的曝光时间拍摄图像时，日光灯的频闪特性会使图像序列产生明显的周期性闪烁。

图像亮度变化的原因，除照明或设备原因导致的非自然闪烁外，还包括因场景变化(如场景角度变化、目标运动和变形)导致的亮度自然变化，多种因素耦合在一起，实现闪烁修正并不容易。在该领域的研究中，闪烁修正多是应用在旧电影修复或监控图像亮度稳定上，其目的一方面是尽量减少画面的明暗变化，避免人眼疲劳，提升观看体验；另一方面，亮度均匀的视频在编码时具有更高的压缩率，可以节省存储空间，易于传输和存档。

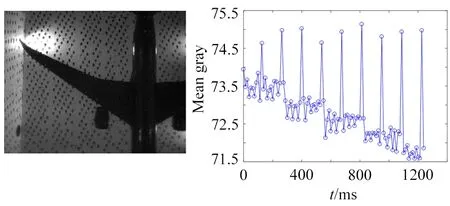
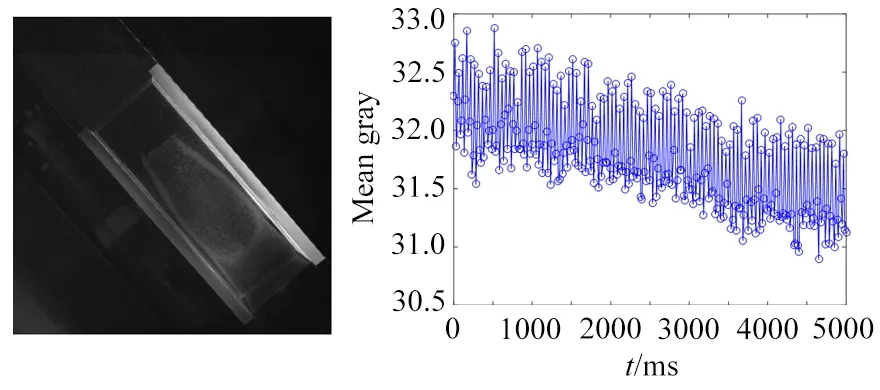
在高速风洞视频测量试验中，通常会安装专用照明设备，但由于试验段周围环境光照条件复杂(干扰源有用于环境照明的日光灯或LED灯，以及监控设备的照明灯等)。由于照明灯的频闪特性，在相机设定的曝光时间较短时，成像很容易出现不同程度的闪烁，造成图像的灰度均值出现周期性变化，如图1(a)～(f)所示，其中图1(a)和(b)分别为标定板图像及其灰度均值变化曲线;图1(c)和(d)为模型变形测量图像及其灰度均值变化曲线；图1(e)和(f)分别为油流试验图像及其灰度均值变化曲线。开展试验时，可采取增强测量专用照明光源的功率、降低干扰光源功率和延长曝光时间这些措施，在一定程度上能够抑制干扰源导致的闪烁,但是前2种方法受硬件条件及测试环境的限制，而延长曝光时间会引入运动模糊，在高速摄影测量中不适用。

(c) (d)

(e) (f)

文献中图像闪烁修正的方法主要分成2类：一类是基于线性或非线性模型的修正方法[1-8]。其原理是通过参数辨识，在基准图像和闪烁图像之间建立仿射模型，利用模型对闪烁图像进行反变换，可得到修正的图像；或者将图像分割成小块，在不同图像的对应块之间建立仿射模型。对于不含运动的图像，其优点是算法简单，处理速度快，主要缺点是基准图像的特性会扩散到整个修复后的图像序列，因此修复效果对基准图像的选择很敏感；对于包含全局运动的图像，需要先全局消抖；对于包含局部运动的图像，需要对运动区域进行识别、分割和运动估计，算法复杂度较高。

在风洞试验中，风洞模型一般为不锈钢材料，表面光滑，缺少可用于图像分块匹配的纹理特征。对于不同帧图像的同一区域，图像之间闪烁导致的亮度变化、模型运动以及相机抖动导致的亮度变化耦合，使得运动检测精度有限，严重限制了模型精度和修正效果，也限制了运动检测的效果。另外，在风洞高噪声振动环境下，需要根据图像中风洞刚性壁板上的标记点坐标解算相机的实际位置和姿态，进而确定模型上标记点的坐标以提高测量精度。因此，视频测量图像是不可以进行全局消抖处理的，这也限制了基于模型方法的应用。

另一类是基于直方图的方法[9-13]，这类方法假定闪烁对整幅图像产生相同或相似的影响，属于全局性的变换方法，因此对图像抖动和局部运动鲁棒性很高。传统的直方图匹配法将闪烁图像的直方图变换成基准图像的直方图来修正闪烁，同样对基准的选择很敏感；直方图平均法将图像的直方图匹配到邻域内多帧图像直方图的平均值，在图像序列亮度存在跳变的情况下不适用[11-12]。假设直方图平均法的邻域宽度为3，如图2所示，从上至下前3幅依次为序列中第n-1、n和n+1帧图像的灰度分布(横轴为灰度值)，可见，图像之间亮度存在跳变。第4幅中红色为平均法得到的第n幅修正图像的灰度分布，明显与期望的修正结果(绿色)不符，损害了图像中的信号。由图1可知，在风洞试验中，存在亮度闪烁的序列相邻帧的亮度在不断跳变，直方图平均法不适用。

图2 直方图平均法的局限

Delon提出了一种尺度时间的直方图均衡方法(Scale-Time Equalization, STE),通过将图像序列的直方图在时间维度上进行高斯卷积变换来修正闪烁，其适应性比直方图平均法强，且修正结果与基准图像无关。通过指定不同的高斯核参数，可以调节修正量，在闪烁和亮度自然变化之间权衡，具有很高的稳定性[11-12]。在视频测量试验中，试验段的背景相对固定，模型在相机视野内运动，其图像全局特征变化很小，因此基于STE的方法比较适用。

本文针对高速风洞视频测量试验图像序列的特点，基于STE方法开展图像闪烁修正技术的研究与应用。

1 STE方法

1.1 直方图匹配

设r和z分别表示变换前的图像f和变化后的目标图像g的灰度级随机变量，其概率密度分别为Pr(r)和Pz(z)。直方图匹配[14]是指将图像f变换到g,并使g具有指定的概率密度Pz(z)。

变换公式为：

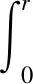
(1)

生成了有均衡化概率密度函数Pq(q)的灰度级随机变量q。T(r)是r所在区间[0,L-1]的严格单调递增函数，且当r∈[0,L-1]时，有T(r)∈[0,L]。

假设z满足：

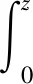
(2)

可得：

z=G-1(q)=G-1[T(r)]

(3)

Pr(r)可通过图像f的直方图统计得到，T(r)可通过式(1)得到，利用式(2)计算G(z)。对于离散图像，可通过统计数据表查询得到其反变换G-1(q)，期间需要对浮点数圆整到[0,L-1]，会对直方图匹配精度造成一定的损失，因此直方图匹配操作得到的是近似具有概率密度Pz(z)的图像g。

1.2 STE

STE利用尺度空间(Scale-Space)理论，针对图像序列中的每一帧实施直方图变换，将其直方图匹配到其目标直方图。每一帧图像的目标直方图由相邻图像的原始直方图进行加权平均得到，其权重就是具有不同尺度参数的高斯核。经过卷积处理，直方图随时间快速变化的细微结构被平滑反映到图像上，就是亮度闪烁被抑制；而目标场景的慢速自然变化，根据尺度参数的选择，可以在一定程度上被保留。

针对图像序列ft，其直方图的STE变换的公式为：

(4)

基于尺度空间理论的STE变换具有如下特性：(1) 前景/背景独立性，即对前景的变换和对背景部分的变换是独立的；(2) 时移不变性，即变换结果与时间起点的选择无关，因此无需预先指定基准图像；(3) 常量不变性，即图像序列没有任何变化，变换结果和原始图像相同。

1.3 图像处理流程

对于试验采集到的离散图像序列fk,k∈[1,N],其中N为序列长度。

处理流程为:

(1) 设定尺度因子s和卷积核的长度l生成高斯卷积核Gs。

图3给出了s取不同值时Gs的形态，可见，参数l确定了参与平滑的邻域帧的数量，增大l时可强化对低频闪烁的抑制；s则决定了在图像之间进行平滑处理时各邻域帧的权重，值越大，去闪烁效果越强，但是也会将图像中的亮度自然变化抑制；反之，则会保留更多的帧间自然变化。

图3 s不同取值时Gs数的形态

(2) 计算图像序列的累积直方图H(k,λ),k∈[1,N],λ∈[0,L-1]，对于8位灰度图像，L=256。

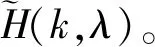
2 实验结果与分析

2.1 校准板图像修正

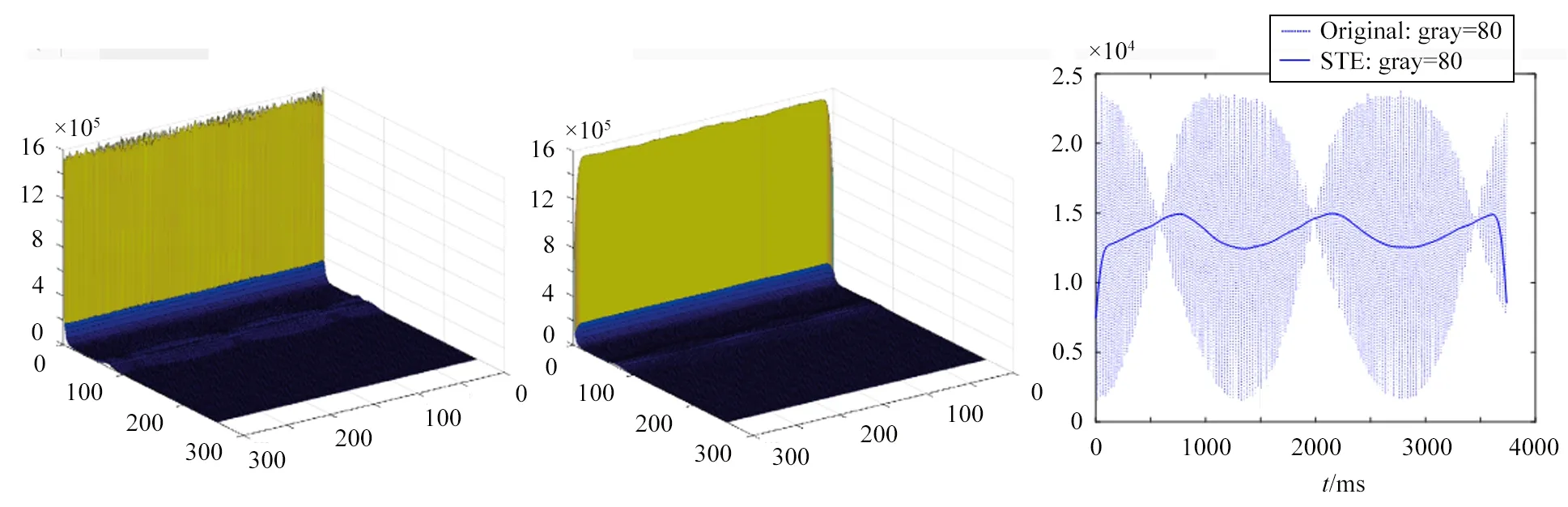
相机校准板图像的拍摄条件为室内环境光加日光灯照明，曝光时间为2000μs，相机成像出现了较强烈的闪烁，如图1(a)和(b)所示。由于照明灯闪烁频率为50Hz，而图像采集频率为80Hz，采样频率较低，因此图1(b)中灰度均值出现了混叠失真。由于标定板位置和姿态固定，整体在日光灯直射和周围墙壁反光的照射下成像，且图像中不存在高光反射点，所以图像的闪烁是全局性闪烁，不存在局部变化的耦合。图4(a)显示了300帧连续图像的灰度直方图，可见，图像各个灰度值的统计值在时间维度上存在剧烈的波动。卷积核参数取l=21,s=8，在执行STE之后，直方图在时间维度上被平滑，如图4(b)所示。

2.2 风洞模型变形试验图像修正

风洞模型变形试验过程中，模型在风洞控制系统的驱动下，其迎角或侧滑角做连续式或阶梯式的变化，在试验采集的图像序列中，试验模型在图像中的位置或姿态在不断改变。因此，即使不存在照明导致的闪烁问题，图像序列中局部区域的统计特征也会随时间出现自然的变化。在试验过程中，通常试验模型只会在相机视野内运动。因此，在不存在闪烁时，整幅图像的统计特征(如灰度直方图)并不会随着模型运动而出现大的变化，故基于STE的闪烁修正方法仍具有适应性。

(a) (b) (c)

(d) (e) (f)

(a) (b) (c)

(d) (e) (f)

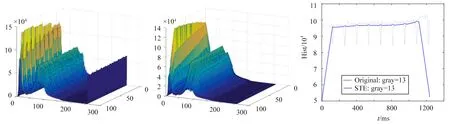
由于试验模型在不断运动，无法像2.1节那样通过相邻帧的差值直观地查看闪烁修正的效果。图5(d)显示了原始图像第21和22帧的差量(为了更清楚地看到差异，差值均被放大了2倍)，模型边缘部分出现了较大的差量带，其宽度即为模型运动导致其成像位置变化的幅度。图像中的模型区是后续分析处理的关键区域，为了避免背景像素的干扰，可以将图像分割成试验模型和背景再进行统计。

对原始图像进行二值化和膨胀、腐蚀、填充等形态学处理，获取试验模型的遮罩图像，如图5(e)所示。将序列中的每一帧图像，利用其遮罩分割为模型和背景区域。分别对原始图像和修正图像的模型区域进行统计，得到图5(f)的灰度均值对比曲线，从图中可以看出，模型区域平均亮度的闪烁幅值被有效抑制。

2.3 风洞动态油流试验图像修正

在动态油流试验中，相机曝光时间设置较短，在环境光的干扰下，试验采集的图像序列出现了闪烁，如图1(e)、(f)和6(a)所示。由于用来分析试验图像的光流法是以运动目标亮度不变为前提，所以闪烁会导致目标对应像素在帧间亮度突变，影响到帧间目标像素的匹配，降低了光流法分析结果的可信度。

在试验过程中，油流图像的油膜区域在模型表面气流的作用下不断地扩散，与2.2节的刚性模型运动不同，其分布形态、厚度和面积都在随时间动态变化。因此，模型区域统计特性的慢速自然变化和闪烁引起的快速变化耦合在一起，在这种情况下，通过采用较小的尺度参数，STE方法可以在抑制闪烁的同时保留油流区域的动态变化特征。

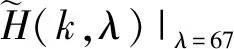
由于油流试验过程中油膜分布形态随动态变化，因此也无法通过相邻帧的差值直观地查看闪烁修正的效果，可以采用2.2节类似的方式，单独对修正前后的图像的模型区域进行统计分析。

和模型变形测量试验不同，空腔油流试验过程中，模型保持静止，因此可以利用固定的遮罩图像(见图6(e))对STE变换前后的图像序列进行分割，然后针对模型区域进行统计。图6(f)给出了针对模型区的灰度均值对比曲线，可以看出，STE处理后，模型区域的亮度闪烁抑制效果良好。

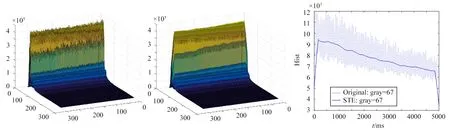
(a) (b) (c)

(d) (e) (f)

本实验结果也证明了对于被摄目标存在形态变化的图像序列闪烁修复问题，STE方法仍具有较好的适应性。

2.4 闪烁修正对标记点定位精度的影响

对于图1(a)中存在强烈闪烁的标定板图像，由于相机和标定板均固定，因此可以用来分析闪烁对定位精度的影响。采用灰度质心法(二值化阈值取50)分别在修正前后计算第96和97帧图像中前100个标记的质心坐标差量，如图7所示。其中修正前差量的均值为0.264pixel，修正后差量的均值为0.173pixel(图像尺寸：5120pixel×5120pixel，标定板长度500mm且成像占满画幅，换算成空间坐标差量分别约为0.026和0.017mm)，减小了34.5%。

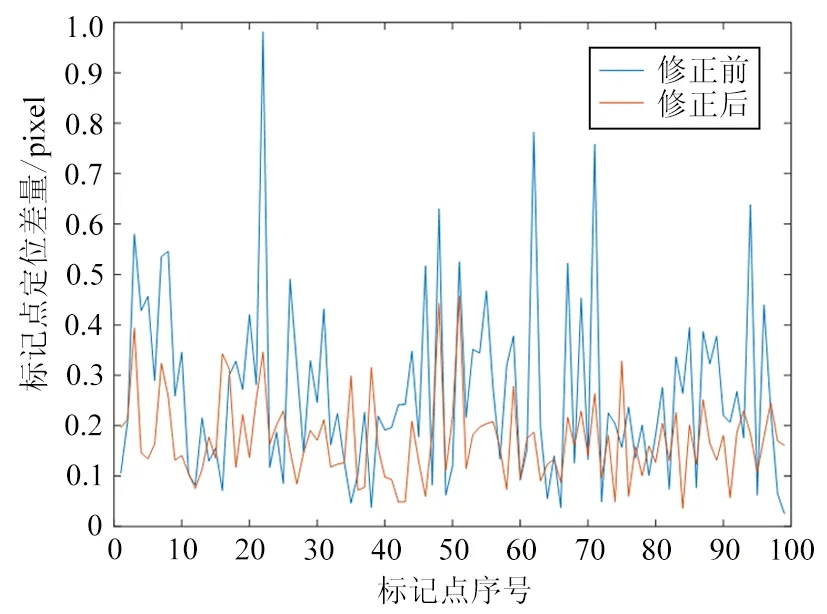
图7 闪烁修正前后标记坐标的差量对比

3 结 论

在高速风洞视频测量试验中的应用结果表明，基于STE的图像序列闪烁修正方法对包含闪烁的图像序列修正效果良好，证明了该方法对于图像抖动、模型局部运动和变形等干扰因素具有较强的鲁棒性。通过调整卷积核参数，可以在抑制图像亮度闪烁的基础上保留场景的自然变化，有利于保留更多图像信息。得益于STE的时移不变性，在修正图像序列前无需指定基准图像、无需运动检测和全局消抖，较基于仿射模型的修正方法，在高速风洞视频测量中更具工程实用性，在摄影测量和机器视觉等领域具有推广应用价值。

参考文献:

[1]孟凤晓. 图像序列中亮度闪烁实时修复[D]. 青岛: 中国石油大学(华东), 2014.

Meng F X. Real-time flicker correction in image sequence[D]. Qingdao: China University of Petroleum (East China), 2014.

[2]黄书锦, 沈一帆. 基于动态范围调整的图像亮度修正方法[J]. 计算机应用与软件, 2014,31(12):265-267.

Huang S J, Shen Y F. Image brightness enhancement based on adjusting dynamic range[J]. Computer Applications and Software, 2014, 31(12): 265-267.

[3]曾敏. 基于非线性模型的闪烁去除技术研究[D]. 大连: 大连理工大学, 2011.

Zeng M. Research on flicker removal technology based on nonlinear model[D]. Dalian: Dalian University of Technology, 2011.

[4]Forbin G, Vlachos T, Tredwell S. Flicker compensation for archived film using a spatially-adaptive nonlinear model[C]. International Conference on Acoustics, Speech and Signal Processing-Proceedings. IEEE, 2006.

[5]Forbin G, Vlachos T. Nonlinear flicker compensation for archived film sequences using motion-compensated graylevel tracing[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2008, 18(6): 803-816.

[6]Zhang R, Wu J, Ding Y, et al. The correction of intensity flicker in archived film[C]. International Conference on Information Technology and Computer Science. IEEE Xplore, 2009: 402-405.

[7]Forbin G, Vlachos T, Tredwell S. Flicker compensation for archived film using a mixed segmentation/block-based nonlinear model[C]. Signal Processing Conference, 2007, European. IEEE, 2015: 135-139.

[8]黄曦, 丁友东, 吴兵. 老电影全局闪烁修复系统的设计与实现[J]. 电视技术, 2016, 40(12):125-129.

Huang X, Ding Y D, Wu B. Implementation and design of old film global flicker restoration system[J]. Video Engineering, 2016, 40(12):125-129.

[10]卢前前. 基于统计分析的视频干扰辨识应用研究[D]. 武汉: 武汉科技大学, 2014.

Lu Q Q. Application research of video interference identification based on statistical analysis[D]. Wuhan: Wuhan University of Science and Technology, 2014.

[11]Delon J. Movie and video scale-time equalization application to flicker reduction[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2006, 15(1):241-248.

[12]Delon J, Desolneux A. Stabilization of flicker-like effects in image sequences through local contrast correction[J]. Siam Journal on Imaging Sciences, 2010, 3(4):703-734.[

13]Papadakis N, Bugeau A, Caselles V. Image editing with spatiograms transfer[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2012, 21(5):2513-2522.

[14]拉斐尔 C 冈萨雷斯, 理查德 E 伍兹. 数字图像处理(第三版)[M]. 阮秋琦, 阮宇智等, 译. 北京: 电子工业出版社, 2007.

Gonzalez R C, Woods R E. Digital image processing[M]. 3rd ed. Beijing: Publishing House of Electronics Industry, 2017.