可弯折翼尖在飞翼布局中操纵性能研究
谢树联 郑君若禹 李 军 /
(同济大学航空航天与力学学院,上海 200092)
0 引言
飞翼布局是仅由单独翼面构成的气动布局形式。相比于其他布局类型,飞翼布局具有结构简单、气动效率高、机动性良好、可探测性低、易于一体化布置等优点。但是,由于取消了尾翼,目前飞翼布局存在气动力和力矩呈现显著非线性、气动力和力矩耦合严重、无安定性、航向操纵性不足等问题,严重制约了飞翼布局的应用。对飞翼布局作战飞机来说,最大的挑战之一就是寻找合适的操控方法代替被取消的垂尾和方向舵,以实现航向的稳定和操控[1]。
为提升无尾飞翼布局飞机的控制能力,美国曾对一些很有前景的操纵装置进行过研究,主要包括全动翼尖、差动前缘襟翼、嵌入面和开裂式方向舵等[5]。目前,国内外有关飞翼布局飞机操控方式的研究主要集中在常规偏航操纵面、发动机推力矢量控制等方面,且两者通常同时使用。常规偏航操纵面如内外升降副翼、开裂式方向舵、全动翼尖、收放式方向舵、嵌入面、差动前缘襟翼、分布式后缘襟翼等主要是通过机翼两侧的差动阻力产生偏航力矩[4],因此进行航向控制时,常规偏航操纵面常会产生一定的阻力增量,降低飞行性能。
为实现飞翼布局航向控制,同时尽量避免产生较大的阻力增量,本文设计了可弯折翼尖作为偏航操纵面,主要通过数值分析对其偏航操纵性能进行研究,为该设计在飞翼布局中的实际应用提供理论和技术基础。
1 研究内容
本文主要研究翼尖弯折对操纵性能的影响,因此机翼设计为固定部分和可弯折部分,以转轴为界,分别称为主翼和翼尖。
如图1所示,两机翼翼尖可实现联动,即同时向上或向下弯折相同角度;亦可实现差动,即两侧机翼翼尖弯折不同角度。

图1 翼尖作动示意图
1) 当翼尖同时向上弯折相同角度时,可以提高飞机飞行的稳定性,亦可起到与翼尖小翼类似的作用,减小翼尖涡流的产生。
2) 当翼尖同时向下弯折相同角度时,会在一定程度上有助于包络住机翼下方气体,提高飞行的机动性。
3) 当翼尖弯折不同角度时,以一侧向上另一侧向下为例,左右两侧主翼和翼尖所受气动力分别为FB1、FS1、FB2、FS2,如图2所示。由此可知,机翼整体受侧向力作用,且可能存在明显的滚转力矩。如此一来,飞机在空中飞行时将会发生横向“漂移”,并且可以通过调节两翼尖的弯折角度来改变航向。

图2 机翼受力情况
2 算法验证
本文研究内容工况较多,因此主要采用CFD计算方法进行分析。为了保证计算结果的可信度,首先对算法进行验证。本文分别采用两种方法进行算法验证。
2.1 实验验证
2.1.1 实验验证模型简化
首先对可弯折翼尖偏航操纵性能进行初步探索,为使计算更加简便,对模型进行简化处理:
1) 忽略机身等部位对机翼气动的影响,模型中舍去机身等部位。
2) 认为左右两片机翼在飞行过程中气动性能是不会相互影响的,在攻角、风速、风向等环境因素均一致的情况下,其气动性能都只与各自可弯折翼尖的弯折角度有关。
3) 整体受力情况是两片机翼受力情况的简单叠加。
4) 采用矩形翼,以便于模型的制作。
基于以上简化方案,只需建立单侧翼尖偏转不同角度的机翼模型即可。
2.1.2 数值分析
根据动力相似性规划待试验模型机翼的尺寸,确定翼展为1 500 mm,弦长为180 mm的近似矩形翼,如图3所示,取攻角为。为使仿真分析结果更为明显,选择了较大升阻比的MH 114翼型。
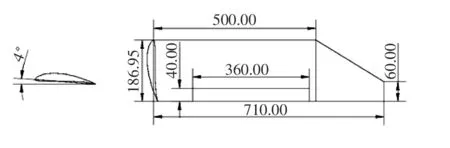
图3 机翼尺寸(长度单位:mm)
应用CATIA以30°为梯度建立梯形翼尖绕垂直于翼展方向的轴旋转90°、60°、30°、0°、-30°、-60°、-90°等一系列机翼模型,并应用ICEM CFD划分网格,采用结构网格,最终生成的网格如图4和图5所示 。

图4 机翼处网格

图5 整体网格
应用Fluent,采用基于压力求解器,Spalart-Allmaras湍流模型进行数值计算。
以0°转角为平衡参照点,得到计算结果如图6所示。由计算结果可知,可弯折翼尖向上或向下弯折不是通过增升或减阻的方式来得到滚转或者偏航的效果,而是直接赋予机翼一个侧向力。

图6 CL~δ,CD~δ,Cy~δ
2.1.3 车载实验
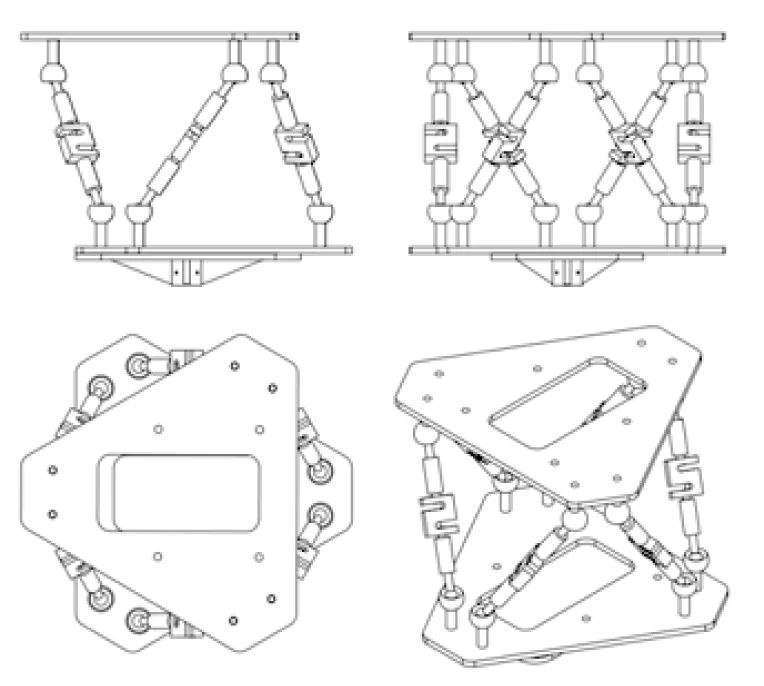
图7 Stewart广义六维力传感器
为使验证结果更加准确,采用自行设计的车载小型无人机气动分析平台(其核心部件是一个Stewart广义六维力传感器,如图7所示,通过六自由度耦合测力得到数据,能避免误差的积累)对矩形机翼模型进行实验,如图8所示。传感器的信号由DH3820高速静态应力应变测试仪提取,再经过降噪和适当处理后耦合计算,由此得到广义力。实验结果如图9所示。

图8 车载实验

图9 车载实验结果
实验结果显示,翼尖相对于中面的弯折角度会造成升力的减少,但对阻力几乎没有影响。另一方面,可得出翼尖弯折角度与侧向力大致呈线性关系,强有力地支持了CFD的分析结果。
2.2 文献验证
本节将对比文献研究结果,进一步验证飞翼翼尖气动性能分析时数值计算方法的可信度。对飞翼布局中可弯折翼尖同样作以下假定:
1) 认为左右机体在飞行过程中气动性能是不会相互影响的,在攻角、风速、风向等环境因素均一致的情况下,其气动性能都只与各自可弯折翼尖的弯折角度有关。
2) 整体受力情况是左右机体受力情况的简单叠加。
2.2.1 数值分析模型
为验证算法的准确性,模型参数基本按照文献[15]进行设置。数值分析模型如图10所示,机身长255 mm,翼展327 mm,前缘后掠角55°,可弯折翼尖面积占全机面积的13.35%,弯折轴线与整机轴线平行,距离112.1 mm;模型参考中心距机身前缘120 mm。所采用翼型为EMX-07。初步验证结果显示,当可弯折翼尖弯折角度在60°~90°和-90°~-60°范围内时,侧向力系数大小基本无变化,故只建立可弯折翼尖弯折-60°、-30°、0°、30°、60°系列模型进行分析。
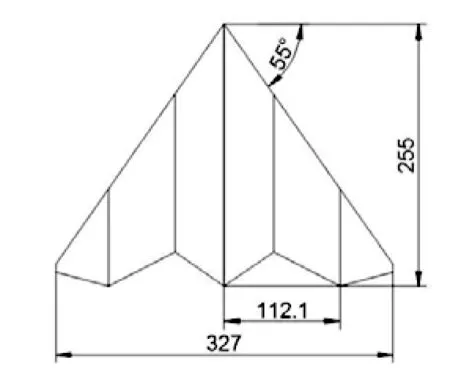
图10 模型尺寸(长度单位:mm)
2.2.2 网格划分与数值算法
运用ICEM CFD进行网格划分,采用非结构网格,建立边界层棱柱网格以满足机体表面粘性边界层的计算要求,并进行局部加密。基于前述假定,采用半模进行分析,半模网格数量约为110万,如图11所示。运用Fluent进行数值计算,采用基于压力求解器,Spalart-Allmaras湍流模型。计算工况为来流速度20 m/s,参考面积0.02 m2,平均气动弦长0.125 9 m。

图11 模型网格
2.2.3 飞机本体气动特性
飞机本体气动特性是指操纵面不作动时,飞机的三轴力和力矩等随攻角的变化规律[15]。
由图12 a)可知,飞机的升力系数CL在α≤16°时基本呈线性增长,在α>16°后逐渐趋于平缓,直至失速,失速迎角为αS=36°,最大升力系数CLmax=1.14。由图12 b)可知,飞机的阻力系数CD在α≤10°时增长较为缓慢,在α>14°时大致呈线性增长。由图12 c)可知,全机的升阻比在α=6°时达到最大,(CL/CD)max=7.72。图12 d)是飞机的俯仰力矩系数特性曲线,曲线斜率始终小于零,飞机是纵向静稳定的。且零升俯仰力矩系数Cm0>0,对飞机的起降有一定的好处。
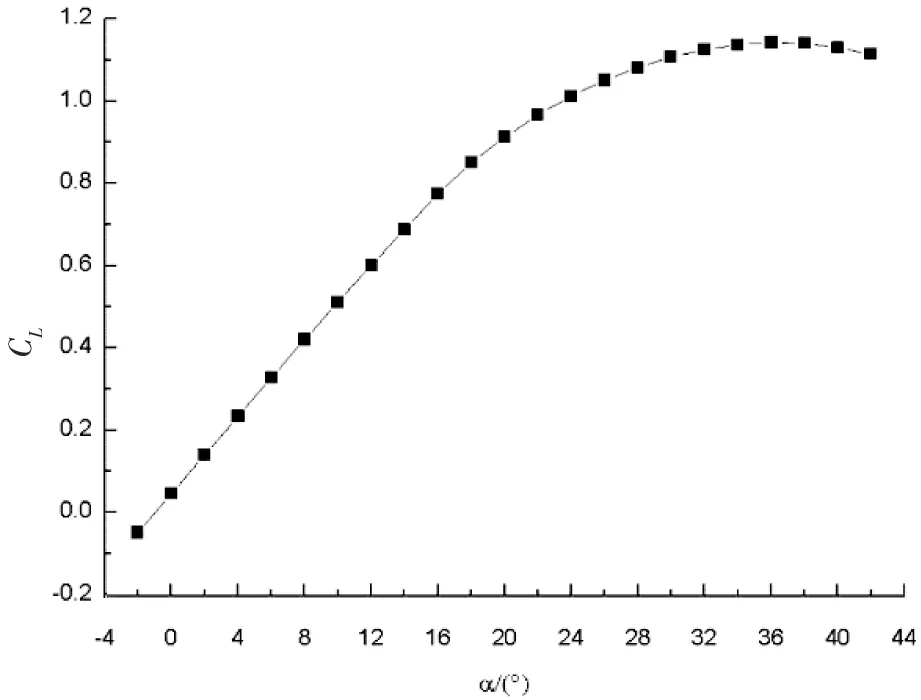
a) CL~α
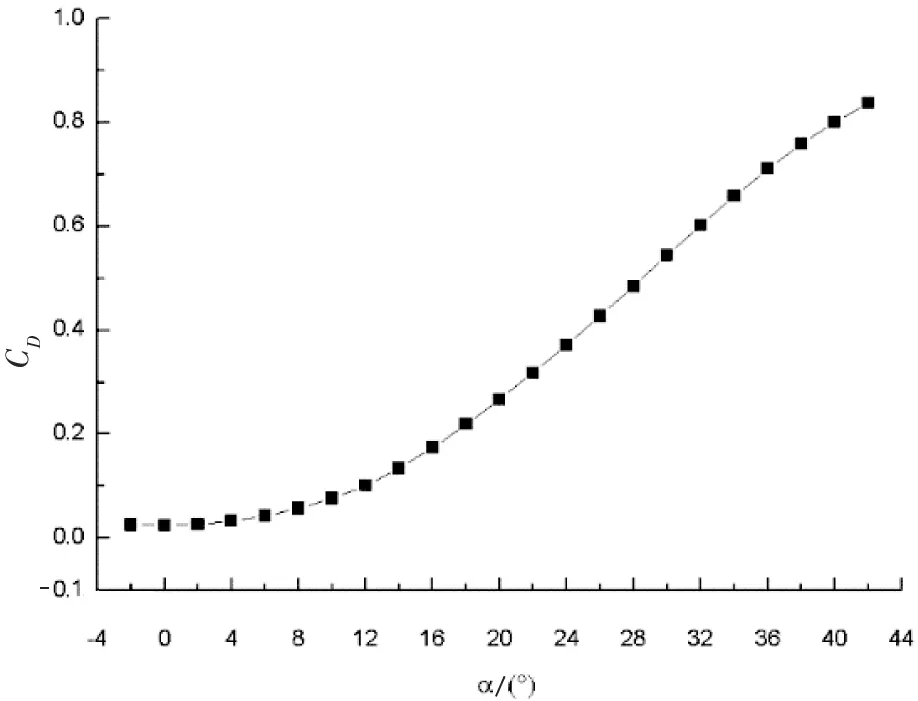
b) CD~α
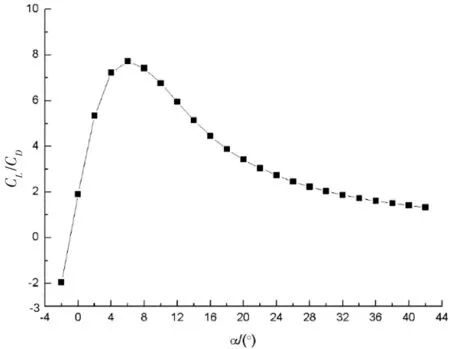
c) CL/CD~α

d) Cm~α图12 飞翼本体气动特性
参照文献[4]中数值分析和风洞实验的结果,在飞翼外形不完全一致、翼型选择不同等情况下,可以认为本文数值分析得到的飞翼本体气动特性结果与上述文献基本吻合,可以用来分析飞翼布局中可弯折翼尖的操纵性能。
3 可弯折翼尖操纵性能分析
前述已说明可弯折翼尖能够实现偏航操纵,以下将对飞翼布局中可弯折翼尖的气动性能进行分析,探究其操纵性。
本文将对可弯折翼尖单侧作动、两侧同向同步作动和两侧反向同步作动进行研究。单侧作动指一侧可弯折翼尖绕轴转动而另一侧保持不变;两侧同步作动指两侧可弯折翼尖保持相同的弯折角度,同向即同时向上或向下,反向则一侧向上一侧向下。基于前述假定,相关数据将由两侧机体简单叠加得到。
3.1 单侧作动
当一侧可弯折翼尖的弯折角度固定为0°单侧作动时,在不同弯折角度δ下升力系数CL与迎角α的关系如图13 a)所示,由图可知,单侧翼尖向上或向下弯折角度越大,升力损失越大,但由于翼尖面积不大,整体升力系数变化不大,升力系数随仰角的变化趋势也基本一致。
在不同弯折角度δ下阻力系数CD与迎角α的关系如图13 b)所示,由图可知,在α<8°时,不同弯折角度下阻力系数基本不变;在 时,单侧翼尖向上或向下弯折角度越大,阻力也就越小,但减小幅度始终较小。这是由于翼尖向上或向下弯折几乎不改变整机的阻力面,同时与许多客机中的翼尖上翘设计类似,起到了减小翼尖扰流的效果,在α≥8°时体现得尤为明显。
在不同弯折角度δ下CL/CD随迎α角的变化如图13 c)所示,可知翼尖弯折对(CL/CD)max对应的攻角无影响。由图13 d)可知,翼尖弯折会削弱俯仰力矩,这是由升力减小而导致的,对飞机保持纵向稳定性略有不利影响,但并不改变俯仰力矩的变化趋势,飞机总体依然保持纵向稳定。
在不同弯折角度δ下偏航力矩系数Cn与迎角α的关系如图13 e)所示,可知翼尖弯折时,在α=0°附近,偏航力矩较小,随着仰角的增大偏航力矩显著增大;在α>12°以后偏航力矩则逐渐趋于平稳甚至略有减小。这是由于在一定的弯折角度δ下,可弯折翼尖的局部攻角随着整机攻角的增大而增大,相应地产生的偏航力矩也就越大;与此同时,可弯折翼尖的横断面与来流方向之间的夹角β也不断增大,当整机攻角增大到一定程度时,β过大而导致偏航力矩不再增大甚至减小。在不同迎角α下偏航力矩系数Cn与弯折角度δ的关系如图13 f)所示,可知弯折角度越大,偏航力矩也越大,且向上弯折时偏航力矩为负,向下弯折时偏航力矩为正。
在不同弯折角度δ下侧向力系数Cy与迎角α的关系如图13 g)所示,在不同迎角α下侧向力系数Cy与弯折角度δ的关系如图13 h)所示,可知翼尖弯折产生侧向力的变化情况与偏航力矩几乎一致,二者变化情况的成因也相同。
在不同弯折角度δ下滚转力矩系数CL与迎角α的关系如图13 i)所示,在不同迎角α下滚转力矩系数CL与弯折角度δ的关系如图13 j)所示,可知在α≤16°时,弯折角度越大,飞行迎角越大,产生的滚转力矩也就越大,且滚转力矩均为负。
由以上分析可知,单侧作动时对升力、阻力、俯仰力矩仅有微小影响,偏航力矩、侧向力、滚转力矩三者之间存在强烈耦合,且三者之间的耦合存在明显的规律性。当单侧翼尖向上弯折时,三者的作用效果均为使飞机航向偏向负方向,可叠加对横航向进行操纵。

a) 不同δ下CL~α

b) 不同δ下CD~α

c) 不同δ下CL/CD~α
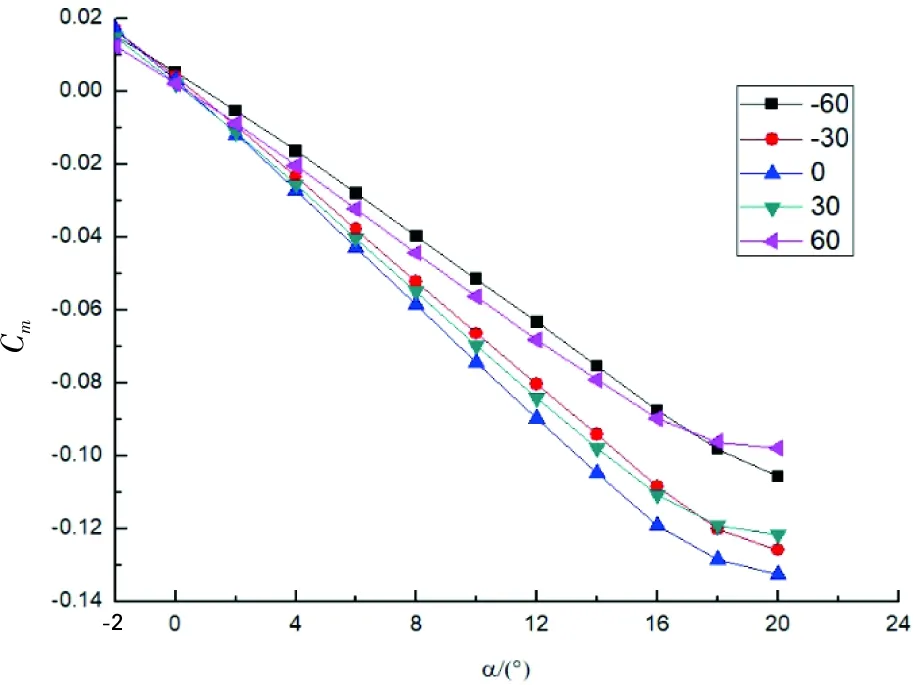
d) 不同δ下Cm~α

e) 不同δ下Cm~α

f) 不同α下Cn~δ

g) 不同δ下Cy~α

h) 不同α下Cy~δ

i) 不同δ下CL~α

j) 不同α下CL~δ图13 可弯折翼尖单侧作动的影响
3.2 两侧同向同步作动
当两侧同向同步作动时,如图14所示,可知升力系数CL、阻力系数CD和俯仰力矩系数Cm的变化规律与单侧作动时基本一致,而变化量大致为单侧传动时的两倍;升阻比CL/CD的变化规律也与单侧作动时基本一致,变化量亦有所增大。由于两侧保持对称,对飞机横航向特性基本没有影响。因此,两侧同向同步作动可在一定程度上用于调节飞机飞行时的升阻关系,甚至能用于切换飞行模式。
3.3 两侧反向同步作动
当两侧反向同步作动时,由图15 a)~图15 d)可知,升力系数、阻力系数、升阻比、俯仰力矩系数的变化情况与两侧同向同步作动时基本一致。

a) 不同δ下CL~α
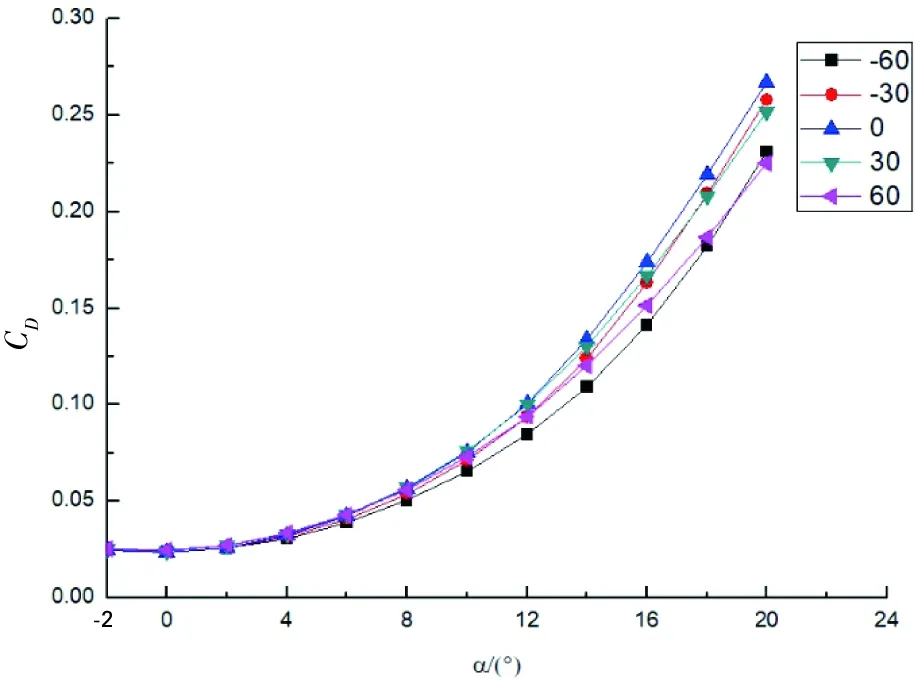
b) 不同δ下CD~α

c) 不同δ下CL/CD~α
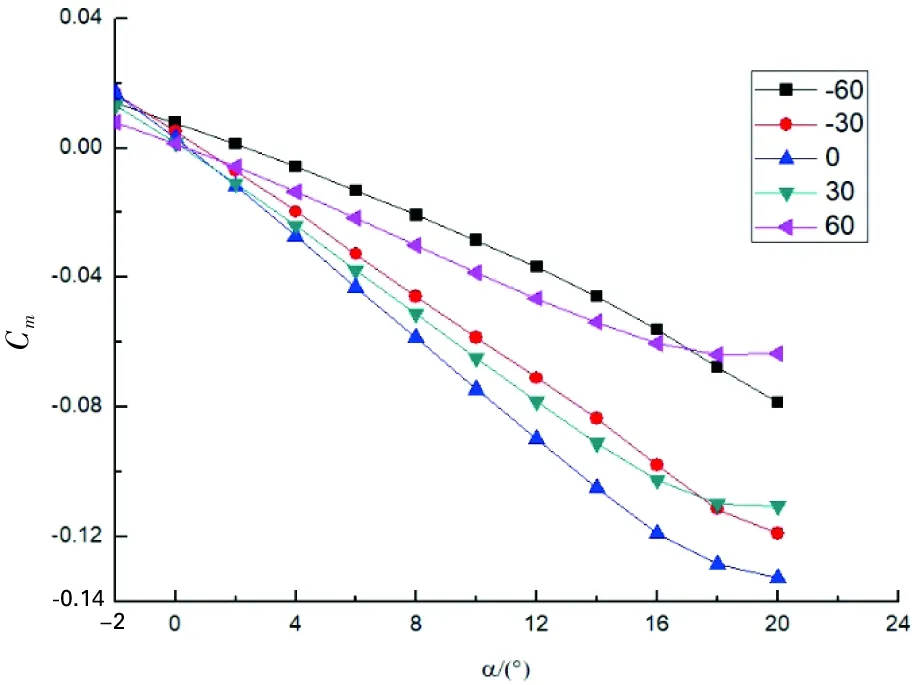
d) 不同δ下Cm~α图14 可弯折翼尖两侧同向同步作动的影响

a) 不同δ下CL~α

b) 不同δ下CD~α

c) 不同δ下CL/CD~α
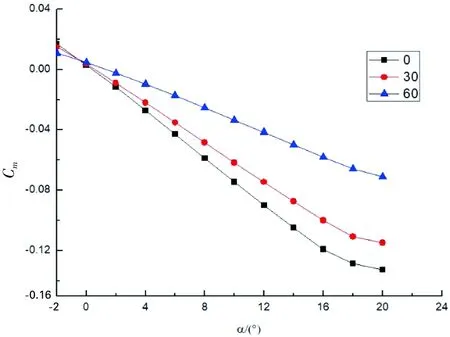
d) 不同δ下Cm~α
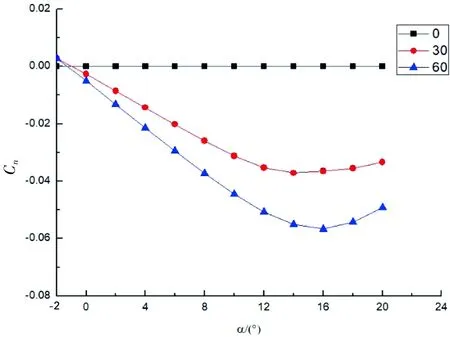
e) 不同δ下Cn~α

f) 不同δ下CL~α
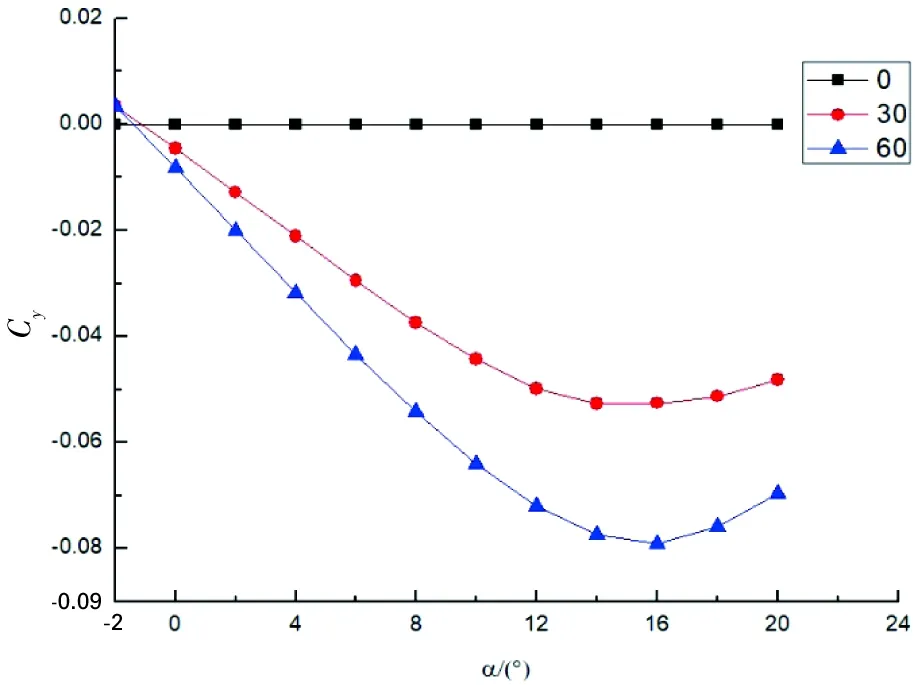
g) 不同δ下Cy~α图15 可弯折翼尖两侧反向同步作动的影响
由图15 e)可知,当迎角α在0°~14°的范围内时,偏航力矩Cn随着α的增大而增大;在α>14°时,偏航力矩Cn不再增大甚至略有减小。形成原因与单侧作动时偏航力矩变化情况的成因一样,只是两侧反向同步作动时偏航力矩的变化同时受两侧可弯折翼尖的影响。
由图15 f)可知,在α≤12°时,滚转力矩CL大小基本保持稳定;在α>12°时,CL迅速下降到0进而反向增大;但CL总体数量级较小,对飞行姿态影响较小。这是由于两侧翼尖弯折形成的滚转力矩方向相反,发生了相互抵消;在α≤12°时,可弯折翼尖向上和向下弯折同一角度时产生的滚转力矩的变化情况都趋近于线性,在二者共同作用下整机滚转力矩能基本保持稳定;当a>12°时,两侧单独作用时滚转力矩的变化情况不一致,从而导致整机滚转力矩突然迅速变化。
由图15 g)可知,侧向力系数Cy的变化规律与偏航力矩基本一致,数值大致为单侧作动时的两倍。
相比于单侧传动,两侧反向同步作动时侧向力和偏航力矩二者之间仍然存在较强的耦合,且二者随弯折角度δ的变化更为明显,而滚转力矩对飞机横航向的影响被大幅削弱,形成了与单侧传动时不同的横航向操纵机制。
4 结论
本文首先通过车载气动实验和文献数据对比分析,验证了CFD计算方法的可信度。然后对飞翼布局中可弯折翼尖的操纵性能进行了研究,得到以下结论:
1) 可弯折翼尖向上或向下弯折不是通过增升或减阻的方式来得到滚转或者偏航的效果,而是直接赋予机翼一个侧向力,可以用于对飞机横航向的操纵。
2) 可弯折翼尖对飞翼布局气动性能的影响存在较大范围的线性段。
3) 和其他阻力操纵面相比,可弯折翼尖不会增加飞翼的整机阻力,甚至能够略微减小阻力,但也会使升力以及升阻比减小,总体而言,对升力、阻力、升阻比的影响都较小。
4) 在可弯折翼尖单侧作动时,偏航力矩、侧向力、滚转力矩三者之间存在强烈耦合,且具有很强的规律性,当单侧翼尖向上弯折时,三者的作用效果均为使飞机航向偏向负方向,可叠加对横航向进行操纵。
5) 两侧反向同步作动时侧向力和偏航力矩二者之间存在较强的耦合,且二者随弯折角度的变化比单侧作动时更为明显,而滚转力矩对飞机横航向的影响相对较小,可形成与单侧传动时不同的横航向操纵机制。
6) 两侧同向同步作动对飞机升力、阻力的影响比单侧作动时更为明显,可在一定程度上用于调节飞机平稳飞行时的升阻关系,甚至能用于切换飞行模式。
参考文献:
[1] BOWLUS J A, MULTHOPP D, BANDA S S. Challenges and opportunities in tailless aircraft stability and control[R]. AIAA 1997-3830,1997.
[2] SERGIO E. Static and dynamic analysis of an unconventional plane-flying wing[R]. AIAA 2001-4010, 2001.
[3] NICKEL K, WOHLFAHRT M. Tailless aircraft in theory and practice[J]. American Institute of Aeronautics & Astronautics E Arnold, 1994.
[4] 张子军,黎军,李天,王晋军. 开裂式方向舵对某无尾飞翼布局飞机气动特性影响的实验研究[J]. 实验流体力学,2010,24(03):63-66.
[5] 单继祥,黄勇,苏继川,李永红,彭鑫. 小展弦比飞翼布局新型嵌入面航向控制特性研究[J]. 空气动力学学报, 2015,33(03):296-301.
[6] 李林,马超,王立新. 小展弦比飞翼布局飞机稳定特性[J].航空学报,2007 (06):1312-1317.
[7] DORSETT K M, MEHL D R. Innovative control effectors (ICE)[R]. WL-TR-96-3043, 1996.
[8] GILLARD W J. Innovative control effectors (Configuration 101) dynamic wind tunnel test report rotary balance and forced oscillation tests[R]. AFRL-VA-WP-TP-1998-3043, 1998.
[9] ADDINGTON G A, MYATT J H. Control-surface deflection effects on the innovative control effectors (ICE 101) design[R]. AFRL-VA-WP-TR-2000-3027, 2000.
[10] DAVIDSON R W. Flight Control Design and Test of the Joint Unmanned Combat Air System X-45A[R]. AIAA 2004-6557, 2004.
[11] 马超,李林,王立新. 大展弦比飞翼布局飞机新型操纵面设计[J]. 北京航空航天大学学报,2007 (02):149-153.
[12] 李忠剑,马东立. 飞翼布局阻力类偏航操纵装置操纵特性分析[J]. 北京航空航天大学学报,2014,40(05): 695-700.
[13] 张彬乾,马怡,褚胡冰,陈真利,陈迎春. 小展弦比飞翼布局航向控制的组合舵面研究[J].航空学报,2013, 34(11):2435-2442.
[14] 马松辉,吴成富,陈怀民. 阻力方向舵在无尾飞机飞行控制中的应用[J].飞行力学,2008 (02):69-73.
[15] 左林玄,王晋军. 全动翼尖对无尾飞翼布局飞机气动特性影响的实验研究[J].空气动力学学报,2010,28(02): 132-137.
[16] 于冲,王旭,陈鹏,苏新兵. 三角翼无尾布局全动翼尖的操纵性能研究[J].航空学报,2012,33(11):1975-1983.

