改进差分进化算法优化BP神经网络用于入侵检测
陈 超 曹晓梅
(南京邮电大学计算机与软件学院 江苏 南京 210023)
0 引 言
入侵检测系统因能快速辨识各种形式的入侵行为而被广泛应用于安全领域,然而随着攻击技术和手段的不断发展与演变,传统入侵检测技术的局限性逐渐显现,针对复杂多样的攻击方式研究新型的入侵检测技术迫在眉睫[1]。
近年来,随着人工智能技术的不断进步,许多专家学者将其引入到入侵检测中并作了大量研究,出现了基于人工神经网络、支持向量机和人工免疫技术等网络入侵检测模型。相比之下,人工神经网络算法具有较强大的自适应、自学习和非线性映射能力,非常适合用于变化无常的网络入侵检测环境,因此基于人工神经网络的入侵检测研究得到了越来越多的关注。吴峻等[2]基于BP神经网络和特征选择技术提出了一种入侵检测模型,实验证明特征选择方法的引入明显提升了BP算法的检测性能。Raman等[3]基于概率神经网络PNN提出了一种新型入侵检测方法HG AR-PNN,该方法综合运用超图技术和神经网络分类技术以提高入侵检测性能。Karimazad等[4]基于径向基函数神经网络RBF和主成分分析技术提出了一种攻击分类检测方法,有效提高了DoS攻击检测的实时性。杨雅辉等[5]基于生长型分级自组织映射神经网络GHSOM提出了一种半监督入侵检测方法,通过少量有标签训练数据引导神经网络结构变化的方式,进一步提高了入侵检测的准确率。
BP神经网络作为当前运用最多、最成熟的神经网络模型之一,因结构简单、高鲁棒性等优点使之应用在安全领域是非常有效的,尤其是入侵检测[2]。然而,传统BP神经网络由于其初始权值阈值是随机初始化的,因此在实际入侵检测应用时会使神经网络收敛速度较慢、训练时间过长。同时,BP神经网络寻优过程中易陷入局部最优值,导致用于入侵检测时检测精度较低[6]。针对上述问题,近年来专家学者多利用一些智能优化算法如粒子群算法[7]、人工蜂群算法[8]、引力搜索算法[9]等来优化BP神经网络,并将优化后的神经网络用于入侵检测,这些方法一定程度上提高了检测的准确性,然而优化算法寻优较慢。而在对较复杂问题的优化上,差分进化算法DE(Differential Evolution)由于算法简单、寻优迅速等优点在各个领域的应用越来越广泛[10-11]。为此,本文将其引入并改进以提升其全局寻优能力,用改进后的DE算法优化BP神经网络,并应用于入侵检测中。
1 相关工作
近年来,为了解决BP神经网络用于入侵检测系统检测性能较差的问题,引入智能算法对BP神经网络进行优化是一个热门课题。刘珊珊等[7]结合BP算法的局部搜索和粒子群算法的全局搜索能力,视种群中每个粒子为BP网络,将粒子的适应度函数设置为BP网络的训练输出均方误差,通过种群中粒子的逐次迭代寻找最优粒子的位置,进而得到最优权值阈值。实验表明,优化算法提高了BP神经网络的泛化能力,一定程度上提升了检测准确率,然而粒子群算法寻优过程中存在收敛精度较低、易发散等缺点。沈夏炯等[8]利用人工蜂群算法优化BP神经网络权值阈值,将每个蜜源视为BP神经网络,蜜源适应度函数设置为BP的误差函数,经过有限次蜜蜂采蜜过程找寻最优蜜源位置对应的权值阈值并赋予BP神经网络。实验表明,所提方法加快了BP神经网络的收敛速度,用于入侵检测时提高了检测精度,然而该文未考虑人工蜂群算法易早熟对于检测结果的影响。Dash等[9]受粒子群算法思想的启发,赋予引力搜索算法中粒子以记忆性和信息共享的能力,利用改进引力搜索算法较强的全局寻优能力对BP网络权值阈值进行优化,将优化后的神经网络用于入侵检测。实验表明,与其他同类方法相比,所提方法在保证对攻击行为较高检测率的同时稳定性良好,然而改进算法一定程度上增加了时间复杂度,导致检测时间稍长。
针对上述问题,本文引入了一种智能优化算法即DE算法。DE算法[12]是由Storn R和Price K于1995年提出的一种具有较强全局搜索能力的启发式优化算法,其基本过程是:将种群中两个随机个体向量间的差分矢量作为随机基准向量的扰动向量,计算得出变异向量,之后变异向量与原始基准向量进行交叉得到试验向量,再通过适应度函数对原始基准向量和试验向量进行择优选择,优质者进入下一代。通过逐次迭代,最终得到最优个体即最优解。然而,在研究过程中也发现,DE算法作为一种基于种群的优化算法,在寻优迭代过程中由于种群多样性的逐渐丧失容易使算法早熟收敛,同时,当优化问题较复杂时,其寻优精度有待提高。
为此,专家学者做了很多改进方案,具体表现在参数动态调整、算法的融合、交叉变异策略改进等方面[13-15]。模拟退火算法SA(Simulated Annealing)是在搜寻过程中,通过定义一种随时间动态改变而逐渐趋向于零的概率突跳性,能在算法陷入局部最优解时概率性的跳出并最终趋向于全局最优。这种特点使得不少研究者将SA与其他智能算法如遗传算法、粒子群算法等融合以开发精度更高的混合智能算法[16-17]。受上述文献启发,为避免DE算法寻优过程中陷入局部最优,本文在标准DE算法的基础上进行改进,在种群经过变异、交叉、选择步骤找寻到当代全局最优个体后,利用SA算法进行二次寻优。同时,为平衡DE算法全局搜索和局部搜索的能力,提高搜索效率,本文引入了一种融合Rand/1和Best/1模式的变异算子。将改进后的算法命名为SAMDE(SA_based Modified DE),并用SAMDE算法优化BP神经网络的权值阈值,将优化的BP神经网络用于入侵检测。同时,为了减少神经网络模型的复杂性,在数据预处理时,利用PCA(Principal Component Analysis)技术对整体样本进行特征提取。本文通过测试函数实验和入侵检测仿真实验分别对SAMDE的优化策略和以其优化BP神经网络并用于入侵检测的可行性进行了分析与验证。结果表明,SAMDE算法优化的BP网络在收敛速度和精度方面有明显提升,用于入侵检测时提高了检测准确率,缩短了训练时间,因而SAMDE算法优化BP神经网络并用于入侵检测是可行的。
2 SAMDE算法优化BP神经网络
采用DE算法优化BP神经网络是利用DE较强的全局搜索能力对BP神经网络初始连接权值阈值进行优化,而优化的目标函数是BP神经网络的输出误差函数。然而,BP输出误差函数所构成的空间是一个较复杂的多极点非线性空间,DE算法在优化较复杂问题时本身也存在易早熟收敛、寻优精度较低等不足[14]。
2.1 SAMDE算法
为提高DE算法的全局寻优能力,本文主要作了两方面改进。一方面,为了有效平衡差分进化算法的全局搜索和局部搜索能力,对变异策略进行改进,提出了一种融合Rand/1和Best/1模式的变异算子,使得算法在进化早期全局搜索能力较强,以有效拓展搜索空间,而在进化后期局部搜索能力较强,保证良好的收敛精度;另一方面,为了避免DE算法陷入早熟收敛,当DE种群经过进化寻找到当代最优个体后,利用模拟退火算法对最优个体进行二次寻优。
2.1.1 融合Rand/1和Best/1模式的变异算子
DE算法变异过程中的变异算子会一定程度上影响算法寻优性能的优劣[18],因此合适的变异算子对于DE算法而言十分重要。在标准DE算法中,DE/rand/1和DE/best/1是两种常用的变异算子,前者有利于保持种群多样性,使DE算法具有较强的全局搜索性能,然而会使算法收敛缓慢。而后者利用最优个体适应度信息,使群体朝最佳适应度个体方向进化,因而算子导向性较好,有利于加快种群收敛速度,然而易使DE算法早熟收敛。从以上分析不难看出,单一的变异算子各有利弊,然而在寻优过程中无法有效平衡全局搜索和局部搜索能力。
鉴于此,本文引入一种结合DE/rand/1和DE/best/1算子的融合算子,则DE变异过程变为:
(1)

在进化过程早期,∂值较小,因此DE/rand/1模式占据主导地位,有利于算法进行搜索范围较广的全局搜索,而伴随着进化过程的进行,∂值逐渐变大,变异算子逐渐倾向于DE/best/1模式,有利于算法进行局部寻优,提高收敛精度和收敛速度。
2.1.2 加入模拟退火操作
随着进化过程的进行,DE算法由于种群多样性的下降容易陷入局部最优值。基于智能互补的原则,本文在标准DE算法的基础上与SA结合,在DE算法找寻到当代最优个体后采用SA的Metropolis准则进行二次搜索,具体实现步骤如下:

zk+1,j=zk,j+random(0,1)×(yjmax-yjmin)j=1,2,…,D
(2)
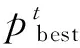
2) 利用模拟退火的Metropolis接受准则进行最优个体的调整:
(3)
式中:f(·)为种群个体适应度函数,本文设置为BP神经网络输出均方误差的倒数。
2.2 改进算法SAMDE的性能测试
本文采用2个经典的测试函数对SAMDE算法进行性能测试,并与标准DE算法进行对比。选用的测试函数F1和F2分别是Sphere函数和Rastrigin函数,具体函数定义见表1。其中F1是单峰二次函数;F2是多峰函数,函数中存在大量局部极小点。

表1 测试函数
借鉴其他相关论文的推荐[13-14]及多次试算,算法相关参数设置如下:种群规模N=100,最大迭代次数gmax=1 000;在DE中,变异因子F=0.6,交叉概率CR=0.7;在SAMDE中,F=0.7,CR=0.6,SA初始温度T0设置为1 000,每个温度段迭代次数L设置为50,降温系数a设为0.99。两种算法在测试函数上的优化收敛曲线分别如图1、图2所示。
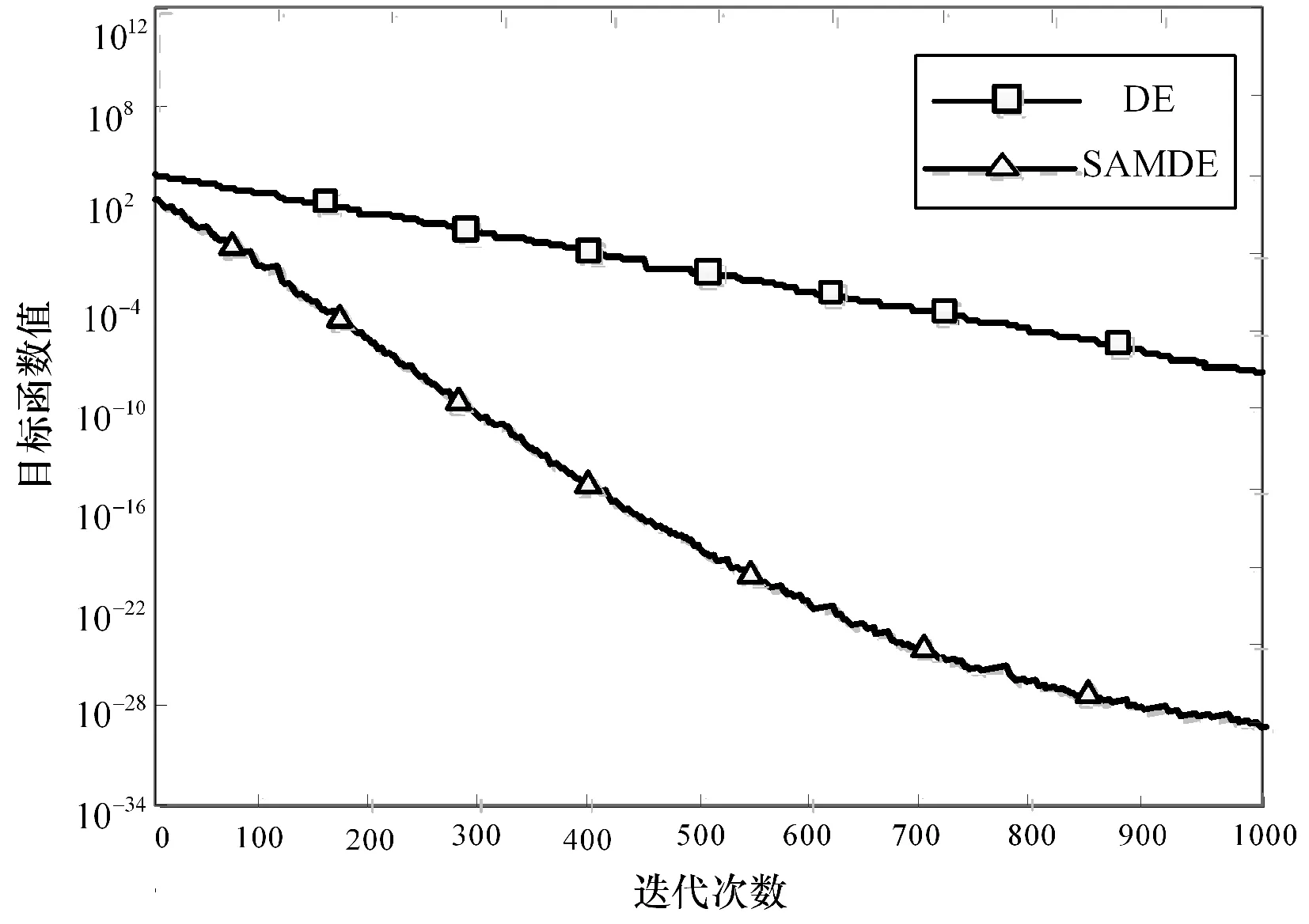
图1 Sphere函数优化收敛曲线图

图2 Rastrigin函数优化收敛曲线图
观察两种算法在优化Sphere函数时的收敛曲线可知,标准DE算法收敛精度较低,而SAMDE算法收敛精度较高,并且几乎是以线性递减的方式收敛到最优解。两种算法在对Rastrigin函数寻优的过程如图2所示,由于函数中存在多个局部最优值,标准DE算法由于跳出局部最优值的能力较差,几乎无法收敛;而SAMDE算法由于模拟退火算法的作用,使得算法能够快速脱离局部极小值,寻优精度最高。通过上述测试结果可知,本文提出的SAMDE算法在全局寻优能力上要强于标准DE算法,这也从侧面体现出本文SAMDE算法的改进策略是可行的。
2.3 SAMDE优化BP神经网络流程设计
利用SAMDE算法优化BP神经网络权值阈值的基本步骤如下:

Step2适应度函数的确定:为表征方便,本文将种群个体适应度函数设为BP神经网络输出均方误差的倒数。


(4)
式中:CR是[0,1]之间的常数,称为交叉因子,j_rand是[1,D]之间的随机整数,用来保证实验个体和变异个体的差异性,D是种群个体向量维数。
Step5选择过程:将实验个体向量和当前演化个体向量解码赋予BP神经网络权值和阈值,并输入训练样本计算各自输出均方误差的倒数。通过适应度函数的比较,将实验个体和当前演化个体按照贪婪方式进行择优选择,方式如下:
(5)
式中:fitness(·)为适应度函数。
Step6种群个体每经过一轮迭代,通过适应度函数的比较会产生当代最优个体,对当代最优个体进行式(2)、式(3)的模拟退火操作,进行最优个体必要的取舍。
Step7通过Step3-Step6的反复迭代,将算法停止时所得到的全局最优个体传回BP神经网络进行再训练并用测试数据进行验证。
测试函数的仿真结果表明了本文SAMDE的优化策略是可行的。然而对于SAMDE优化BP并用于入侵检测的性能效果还需要进一步的实验验证,因此本文首先提出了一种基于SAMDE-BP算法的入侵检测模型,其次为算法在用入侵检测时的实际分类效果设计了仿真实验。
3 基于SAMDE-BP算法的入侵检测
本文提出一个基于SAMDE-BP算法的入侵检测模型,如图3所示,其中主要包括数据捕获引擎、特征提取模块、数据预处理、样本数据库、SAMDE-BP模型训练模块、SAMDE-BP模型检测模块和响应模块。

图3 基于SAMED-BP算法的入侵检测模型
• 特征提取模块:主要负责从数据流中提取能准确代表该数据流的特征向量。
• 数据预处理模块:主要负责对特征向量进行处理,分为两步:首先要对特征向量每个维度字段数值归一化到一个较小的区间中;其次需要利用PCA降维技术进行数据样本的压缩处理。
• SAMDE-BP模型训练模块:主要负责从样本数据库中提取训练样本对模型进行训练。
• SAMDE-BP模型分类器可以对输入的预处理过后的网络数据流特征向量判别为正常或异常。
• 告警模块主要负责将入侵事件及时告知管理员,并对未知类型入侵行为向管理员发出提示。
本文重点是设计SAMDE-BP模型分类器,其基本原理是用划分好类别的训练样本对SAMDE-BP模型进行训练,从而建立起对于攻击类型数据流的识别模型;然后对在线捕获的网络数据流输入分类器进行分析处理,进而判断出是正常还是异常的网络行为。
4 仿真实验与结果分析
本文着重于分析所提出的混合入侵检测算法SAMDE-BP对于入侵行为的检测效果,仿真实验环境为Windows 7,用Matlab 2014a作为仿真平台,实验数据采用KDD_Cup99[19]网络入侵数据集,数据集中共有约500万条连接数据记录,其中每一条记录均包含41个特征属性和1个类标签属性,数据集总共包含了四种攻击方式,分别是拒绝服务攻击(DoS)、未经授权的远程访问(R2L)、本地超级用户的非法访问(U2R)和刺探攻击(PROBING)。
4.1 实验数据及预处理


表2 训练及测试数据集抽取数目表
由于获取的网络数据流特征向量不仅维度高,而且数据向量众多分量之间存在冗余的相关关系,若不进行数据的降维处理,势必会增加神经网络模型的复杂性。因此仿真实验利用MATLAB对训练数据集作进一步PCA特征提取处理,统计主成成分累计贡献率大于90%的主成分个数。篇幅所限,降维过程不再赘述。实验结果显示前7个主成分的累计贡献率为92.1%,已经能较好表征数据集的主要信息,因此本文提取前7个主成分,选取其特征值对应的特征空间的投影值,并从投影后的空间选取训练数据和测试数据输入BP神经网络进行训练及测试[7]。
4.2 实验结果及性能分析
4.2.1 寻优效果及收敛速度对比实验
研究表明,对任何一个在闭区间内的连续函数都可以用单隐层的BP网络逼近,因此本文的BP神经网络采用经典的三层网络结构[20]。由于PCA特征提取后数据维度变成7维,因此BP神经网络输入层节点数设为7。检测的目的是为了区分正常还是异常,因此将输出神经元数目设为1,学习率设为0.1,目标误差设为0.01,最大循环次数设为1 000;对于SAMDE算法,通过相关文献的建议及多次试算,将变异因子设为0.6,交叉概率设为0.7,模拟退火的初温T0由群体特征信息确定;对于BP网络隐含层节点而言,学术界暂无权威的标准设置方式,笔者通过设置不同的隐含层节点数进行多次训练试算,截取部分实验结果如表3所示。
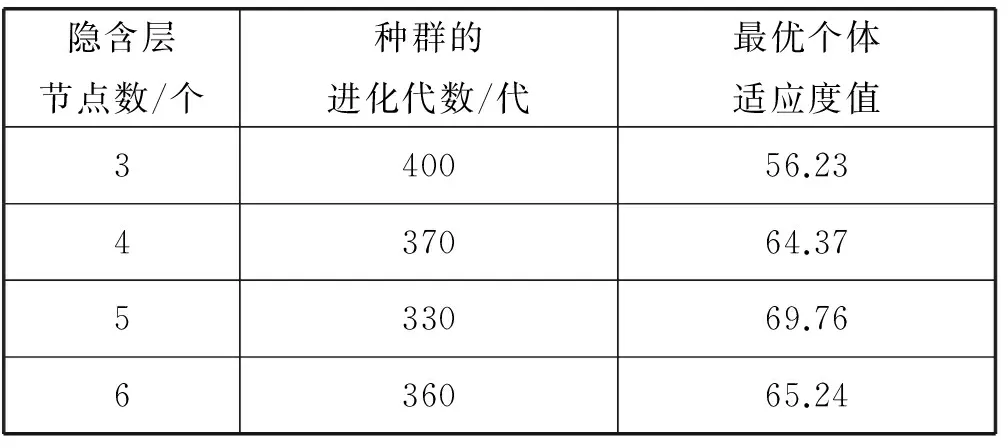
表3 BP不同隐含层参数取值的实验结果比较
由表3可知,当隐含层节点数目为5,进化代数为330代时,种群全局最优个体适应度值最好,迭代次数较少,因此设置本文SAMDE-BP网络隐含层节点个数为5,则优化后的BP网络结构为“7-5-1”。将全局最优个体解码为BP权值阈值,输入训练集对BP进行再训练,直至达到指定误差。图4为改进前后差分进化算法对于BP权值阈值的寻优性能示意图,图5为优化前后BP神经网络训练结果示意图。
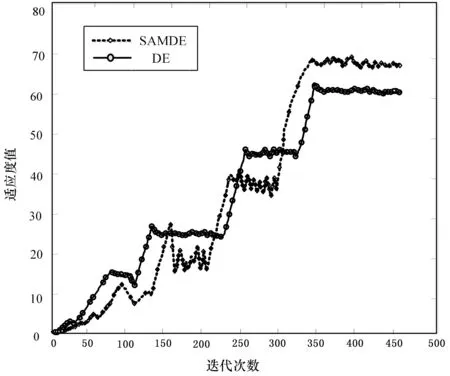
图4 改进前后DE寻优效果对比

图5 优化前后BP算法收敛速度对比
由图4可知,改进后的SAMDE算法相比标准DE算法在找寻BP最优权值阈值时具有更好的适应度值,因此寻优能力更强。由于BP神经网络随机初始化权值阈值,通过梯度下降法调整权值阈值,由图5可知,未优化的BP神经网络在寻优过程中陷入了局部最优,训练精度到达10-1后便停滞不前;经过DE和SAMDE优化后的BP神经网络收敛速度加快,收敛精度提高;SAMDE在一定程度上提高了DE的全局寻优能力,使得优化后的BP神经网络在不足300次迭代后就达到收敛,收敛速度最快且收敛精度较BP相比有大幅度提升。
4.2.2 算法性能及检测性能对比实验
为了分析本文SAMDE-BP融合算法的性能开销,对算法在运行过程中对内存的占用和训练运行时间进行统计,并与标准BP算法进行了对比。内存占用情况的比较结果如图6(a)所示,由于SAMDE需要申请额外的内存空间以存取种群信息,因此较BP相比,SAMDE-BP需要消耗较多的内存空间。两种算法的训练时间比较如图6(b)所示,标准BP算法使用梯度下降法进行神经网络误差传递更新权重过程,时间复杂度较高,而本文改进差分进化算法寻优速度快,替代了梯度下降法复杂的权值阈值更新过程,一定程度上缩短了训练时间。

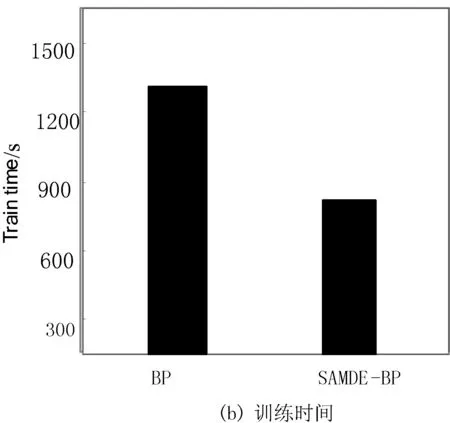
图6 算法性能分析
为表征本文融合算法SAMDE-BP的入侵检测效果优劣,将经过PCA处理后的相同测试数据输入检测模型进行测试。将本文融合算法与BP和DE-BP进行检测结果的对比分析,对每种算法分别训练20次,检测结果取平均值。设定统一的实验参数值,参数设置见4.2.1节。对分类结果使用检测率、误报率、漏报率、训练周期四个指标进行评价。同时约定当BP神经网络输出神经元输出范围是[0,0.5]之间时判断为0,代表正常;而当输出范围是[0.5,1]时则将其判断为1,代表异常。检测率、误报率和漏报率分别定义如下,实验结果如表4所示。
检测率=正确检测出的各类样本数/样本总数
误报率=误报为入侵的正常样本数/正常样本实际总数
漏检率=误判为正常的入侵样本数/入侵样本实际总数

表4 模型检测性能对比结果
与BP相比,本文融合算法检测率升至96.12%,误报率和漏报率分别降至2.89%和2.32%,训练时间由1 320 s缩短至585 s。实验过程中也发现,几种模型的入侵检测效果均受BP网络的初始权值阈值影响,而经过SAMDE算法优化过的BP神经网络由于具有较好的初始权值阈值,因此训练过程提高了收敛速度和预测精度,缩短了训练时间。由于R2L和U2R训练数据数量较少,所以最终导致测试时这两种方式的检测率较低,误报率较高,一定程度上影响了整体的检测效果。总体而言,由表4测试结果可知,本文的SAMDE-BP检测模型检测率最高,误报率和漏报率相对较低。
5 结 语
针对BP神经网络应用于入侵检测时检测率较低、训练时间过长的问题,提出了一种改进差分进化算法(SAMDE)优化BP神经网络的入侵检测算法。首先通过测试函数实验表明利用融合变异算子和加入模拟退火操作对DE算法进行改进是可行的,一定程度上提升了其全局寻优能力。其次入侵检测仿真对比试验表明本文算法优化的BP网络在收敛速度和精度方面有明显提升,用于入侵检测时提高了检测准确率,缩短了训练时间,因此SAMDE优化BP神经网络并用于入侵检测是可行的。由于差分进化算法需要申请额外的内存空间以存取种群信息,因此SAMDE-BP需要消耗较多的内存空间,并且由于融入了模拟退火操作,一定程度上增加了算法的时间复杂度,下一步将研究如何有效降低融合算法的空间和时间复杂度。
[1] Ashfaq R A R,Wang X Z,Huang J Z,et al.Fuzziness based semi-supervised learning approach for intrusion detection system[J].Information Sciences An International Journal,2017,378(C):484-497.
[2] 吴峻,李洋.基于BP神经网络和特征选择的入侵检测模型[J].计算机工程与应用,2008,44(30):114-117.
[3] Raman M R,Somu N,Kirthivasan K,et al.A Hypergraph and Arithmetic Residue-based Probabilistic Neural Network for classification in Intrusion Detection Systems[J].Neural Networks,2017,92:89-97.
[4] Karimazad R,Faraahi A.An Anomaly-Based Method for DDoS Attacks Detection using RBF Neural Networks[C]//International Conference on Network and Electronics Engineering,2011,11:44-48.
[5] 杨雅辉,黄海珍,沈晴霓,等.基于增量式GHSOM神经网络模型的入侵检测研究[J].计算机学报,2014,37(5):1216-1224.
[6] Gu Y,Shi Y,Wang J.Efficient Intrusion Detection Based on Multiple Neural Network Classifiers with Improved Genetic Algorithm[J].Journal of Software,2012,7(7):1512-1516.
[7] 刘珊珊,谢晓尧,景凤宣,等.基于PCA的PSO-BP入侵检测研究[J].计算机应用研究,2016,33(9):2795-2798.
[8] 沈夏炯,王龙,韩道军.人工蜂群优化的BP神经网络在入侵检测中的应用[J].计算机工程,2016,42(2):190-194.
[9] Dash T.A study on intrusion detection using neural networks trained with evolutionary algorithms[J].Soft Computing,2017,21(10):2687-2700.
[10] Hung Y C,Lin F J,Hwang J C,et al.Wavelet Fuzzy Neural Network With Asymmetric Membership Function Controller for Electric Power Steering System via Improved Differential Evolution[J].Power Electronics IEEE Transactions on,2015,30(4):2350-2362.
[11] Liu W,Song H,Liang J J,et al.Neural Network Based on Self-adaptive Differential Evolution for Ultra-Short-Term Power Load Forecasting[M]//Intelligent Computing in Bioinformatics.Springer International Publishing,2014:403-412.
[12] Das S,Mullick S S,Suganthan P N.Recent advances in differential evolution-An updated survey[J].Swarm & Evolutionary Computation,2016,27:1-30.
[13] 胡中波,熊盛武.基于模拟退火的混合差分演化算法研究[J].计算机工程与设计,2007,28(9):1989-1991.
[14] Wang L,Zeng Y,Chen T.Back propagation neural network with adaptive differential evolution algorithm for time series forecasting[J].Expert Systems with Applications,2015,42(2):855-863.
[15] Wu Z,Wu Z,Zhang J.An improved FCM algorithm with adaptive weights based on SA-PSO[J].Neural Computing and Applications,2016,28:3113-3118.
[16] Goudarzi S,Wan H H,Anisi M H,et al.MDP-Based Network Selection Scheme by Genetic Algorithm and Simulated Annealing for Vertical-Handover in Heterogeneous Wireless Networks[J].Wireless Personal Communications,2017,92(2):399-436.
[17] Geng J,Li M W,Dong Z H,et al.Port throughput forecasting by MARS-R SVR with chaotic simulated annealing particle swarm optimization algorithm[J].Neurocomputing,2015,147(1):239-250.
[19] 王洁松,张小飞.KDDCup99网络入侵检测数据的分析和预处理[J].科技信息:科学·教研,2008(15):409-410.
[20] Saad R M A,Anbar M,Manickam S,et al.An Intelligent ICMPv6 DDoS Flooding-Attack Detection Framework (v6IIDS) using Back-Propagation Neural Network[J].Iete Technical Review,2016,33(3):244-255.

