城市高架连续钢箱梁计算分析

熊 诚，汪 斌，梁庆学

（1.中国市政工程中南设计研究总院有限公司，湖北 武汉 430010；2.长江勘测规划设计研究有限责任公司，湖北 武汉 430010）

0 引言

近年来，城市高架道路系统得到了飞速发展，由高架道路组成的城市快速路或主干路在城市交通中发挥着举足轻重的作用。在城市高架道路设计中，特别在交通繁忙的路口建造立交桥，受施工条件、工期、桥下地面交通组织和桥梁总体美观等多方面因素的限制，结构总体设计多采用跨越能力较强、施工快捷的连续钢箱梁方案。

本文以某城市高架三跨连续钢箱梁为工程实例，采用MIDAS/Civil建立有限元分析模型，对结构进行详细计算分析。

1 工程概况

某城市高架桥第一联跨越现状高速公路，采用三跨连续钢箱梁结构，联长120m，桥跨布置为35m+50m+35m=120m，桥宽26m。桥梁总体布置如图1所示。

主梁采用单箱三室斜腹板钢箱梁截面，梁高1.92m；箱梁跨中标准截面顶板、底板、腹板厚均为14mm，支点段顶板、底板、腹板加厚至24mm。顶板、底板间距560mm设置一道加劲肋，加劲肋采用U形肋，板厚12mm，肋高约280mm。腹板间距500mm设置一道I形加劲肋，板厚12mm，肋高120mm。箱梁沿纵向间距2.5～3.0m设置一道横隔板，板厚14mm。钢箱梁标准横断面及纵剖面如图2和图3所示。

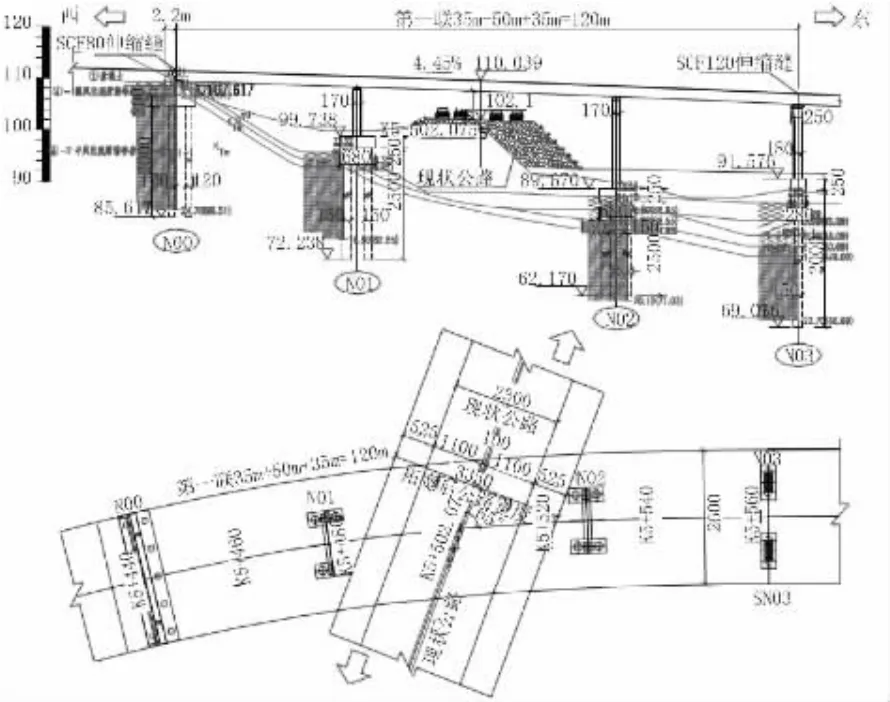
图1 总体布置图（单位：cm）

2 计算模型建立

采用MIDAS计算软件将结构离散为空间梁单元，建立全桥有限元模型，共126个单元、135个节点。边界条件的自由度约束均按设计图纸设置，采用双支座模拟。有限元模型如图4所示。

桥梁荷载取值如下：主梁自重由程序自动计算；二期荷载包括防撞护栏与桥面铺装，以均布荷载计入；汽车荷载为城-A级，双向六车道；温度作用包括整体升温、降温及梯度温度，取值按照《公路桥涵设计通用规范》（JTGD60—2015）执行；汽车冲击系数μ=0.195；基础不均匀沉降按1cm考虑。

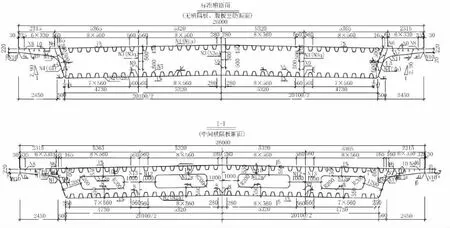
图2 钢箱梁典型横断面图（单位：mm)

图3 钢箱梁纵剖面图（单位：mm)

图435 m+50m+35m=120m连续钢箱梁有限元分析模型图

3 计算内容及结果分析

3.1 纵向计算分析

3.1.1 第一体系应力（主梁体系）

钢箱梁沿纵向整体受力，其受力特性为连续梁特性，跨中正弯矩最大，支座负弯矩最大。采用空间单梁模型，计算箱梁上下缘的最大正应力。计算结果如图5～图8所示。

图5 主梁剪力包络图（单位：kN）

图6 主梁弯矩包络图（单位：kN·m）

图7 截面上缘正应力（单位：MPa）

图8 截面下缘正应力（单位：MPa）

剪应力考虑均由各腹板平分承受。

边支点处：腹板厚 14mm，τmax=78.3MPa。

中支点处：腹板厚 24mm，τmax=75.6MPa。

3.1.2 第二体系应力（桥面体系）

钢桥面板作为桥面系直接承受车轮荷载作用，因此由纵肋和顶板组成结构系，把桥面上的荷载传递到横隔板上。针对这一体系，把横隔板间的单根纵肋及一定宽度的桥面板作为整体，将横隔板作为支撑，计算其在外荷载作用下的应力。因为纵肋穿过横隔板保持连续，因此纵肋具有连续梁特性。按多跨刚性支承连续梁计算纵肋弯矩，跨度为横肋间距a=3000mm，采用MIDAS/Civil程序计算，弯矩包络图如图9所示。

经计算，纵肋最大正弯矩处上缘压应力为46.6MPa，下缘拉应力为108.4MPa；最小负弯矩处上缘拉应力为36.1MPa，下缘压应力为83.8MPa。

3.1.3 应力叠加结果分析

第一、第二体系面应力叠加结果见表1。

图9 纵肋恒载+活载弯矩包络图（单位：kN/m）

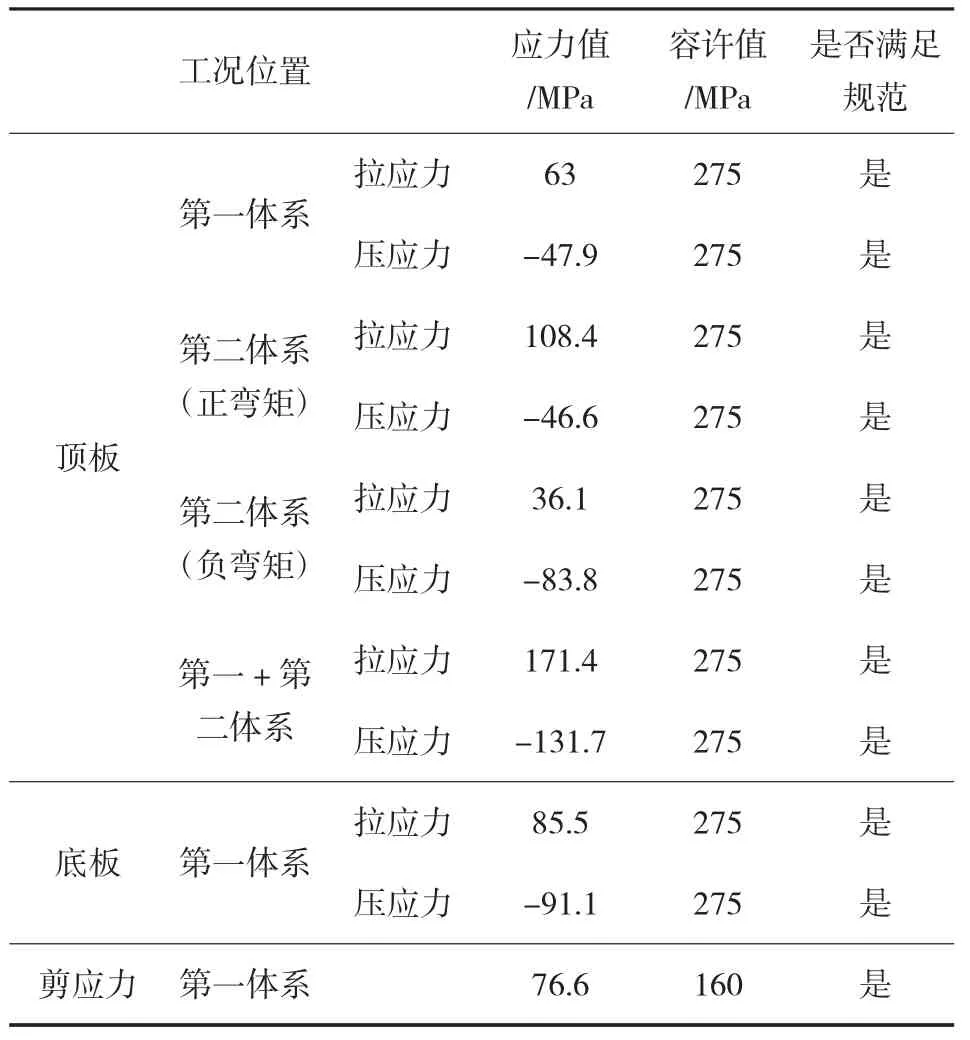
表1 主梁截面应力叠加结果表（第一、第二体系）

3.2 横向计算分析

3.2.1 普通横隔板

普通位置横隔板承受纵肋传递过来的力，再传递到两侧腹板上，横隔板横向受弯，可简化为两端简支于腹板的简支梁计算。内力计算图如图10所示，弯矩及剪力包络图如图11和图12所示。

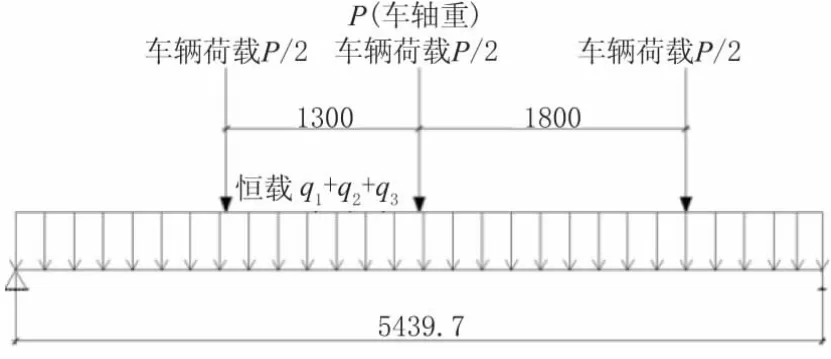
图10 横隔板内力计算示意图（单位：mm）

图11 横隔板弯矩包络图（单位：kN·m）

图12 横隔板剪力包络图（单位：kN）

跨中截面：上缘压应力10.8MPa，下缘拉应力10.8MPa。支点截面：最大剪应力 27.7MPa。

3.2.2 支点横梁

支点横梁承受腹板传递的力，再传递给支座，支点横梁横向受弯，可简化为简支于支座上的简支梁或者连续梁，承受腹板的竖向力。支点横梁为两块横隔板或三块横隔板组成，截面为箱形截面。腹板的竖向力大小按该支座处的总支反力平分（乘以一定的偏载系数）。中横梁、端横梁等效截面如图13所示。

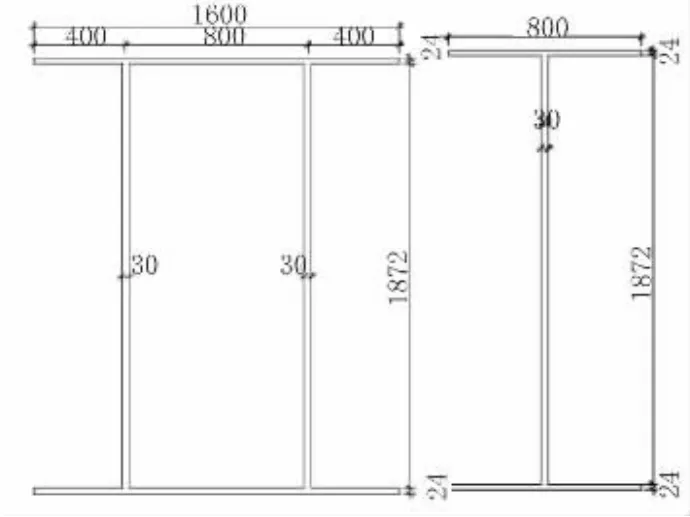
图13 中横梁、端横梁等效截面（单位：mm）

经计算，中横梁腹板最大剪应力68MPa，上缘最大拉应力144MPa，下缘最大压应力144MPa；端横梁腹板最大剪应力28MPa，上缘最大拉应力121MPa，下缘最大压应力121MPa。

3.3 支撑加劲肋

钢箱梁在支承处应设置成对的竖向加劲肋。支承加劲肋直接承受支座反力的作用，不仅需要验算支承垫板处腹板和加劲肋的直接承压应力，而且必须计算腹板和加劲肋中的竖向应力。

依据《公路钢结构桥梁设计规范》（JTGD64—2015）第5.3.4条，经计算中支点、边支点局部承压应力分别为74.2MPa、31.2MPa。中支点、边支点处加劲肋竖向应力分别为186MPa、78.1MPa。支撑加劲肋计算时腹板有效计算宽度如图14所示。

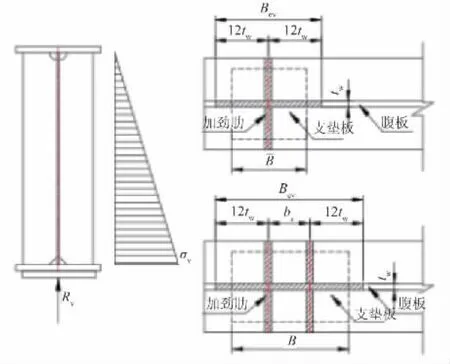
图14 支撑加劲肋计算时腹板有效计算宽度

3.4 刚度验算

依据《公路钢结构桥梁设计规范》第4.2.3～

4.2.4 条验算主梁刚度。

中跨恒载作用下的挠度δ=28mm。

中跨汽车荷载作用下的最大挠度δ=15.4mm＜[δ]=50000/500=100（mm）。

中跨设预拱度，预拱度值为28+15.4/2=35.7（mm）。

3.5 抗倾覆验算

由于该桥位于R=500mm曲线段且横向支座间距偏小，需对该桥进行抗倾覆验算。依据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（2012版征求意见稿）第4.1.10条说明，对于正交桥梁，倾覆轴线为位于箱梁桥中心线同侧的桥台支座连线。本桥倾覆轴线如图15所示。

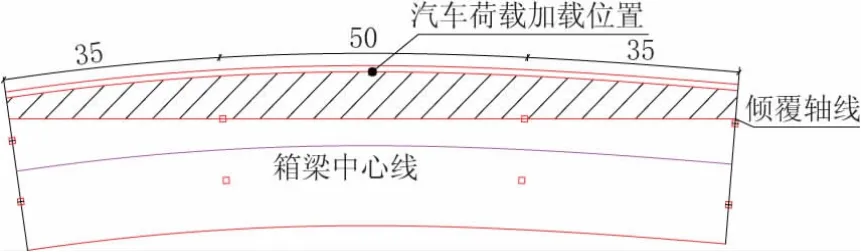
图15 桥梁倾覆轴线示意图（单位：m）

经计算，抗倾覆安全系数为13.3＞2.5。

4 结语

（1）根据纵向计算（第一体系）应力计算结果，主梁全截面最大拉压应力均小于钢材弯曲应力容许值275MPa，表明主梁梁高及底板厚度满足要求。腹板剪应力小于容许值160MPa，表明腹板个数及厚度满足要求。

（2）根据纵向计算（第一、第二体系）应力叠加计算结果，顶板正应力小于规范容许应力值，表明顶板厚度满足要求。

（3）根据纵向计算（第二体系）应力计算结果，纵肋正应力小于规范容许应力值，表明顶板加劲肋间距及横隔板纵向间距（纵向加劲肋跨度）满足要求。

（4）根据横向计算结果，普通横隔板及横梁正应力及剪应力均小于规范容许应力值，表明横隔板间距及厚度均满足要求。

（5）依据支撑加劲肋计算结果，加劲肋承压应力及竖直应力均小于规范容许应力值，表明加劲肋设置合理。

（6）通过桥梁刚度及抗倾覆稳定计算结果，可知该桥刚度及抗倾覆验算均满足规范要求。

参考文献：

[1]项海帆.高等桥梁结构理论（2版）[M].北京：人民交通出版社，2013.

[2]吴冲.现代钢桥：上[M].北京：人民交通出版社，2006.

[3]贾高炯.钢箱梁桥[M].北京：人民交通出版社，2016.

[4]吉伯海，傅中秋.钢桥[M].北京：人民交通出版社，2016.