无机结合料稳定类基层沥青路面结构计算图示研究*

李 浩 刘 锋 许新权 吴文伟

(公路交通安全与应急保障技术及装备交通运输行业研发中心1) 广州 510420)(广东华路交通科技有限公司2) 广州 510420)

0 引 言

文献[1]以路表弯沉、沥青层底拉应力和无机结合料层底拉应力为设计指标，通过计算轮隙中心处路表弯沉、轮隙中心或单圆荷载中心处的层底拉应力以验算路面厚度.现行规范提供的计算点位少、点位间距大，也没有明确待计算指标的方向，难以满足荷载下沥青路面结构内部应力应变响应规律的研究[2-5].

然而，根据国内外对无机结合料稳定类基层沥青路面设计方法的研究成果[6-10]，设计指标可分为两类：①疲劳寿命，根据沥青层或基层的层底拉应力或拉应变验算结构的疲劳寿命；②沥青层永久变形量，综合考虑沥青层竖向应力、应变及剪应力、剪应变等因素验算沥青层永久变形量.

本文通过加密计算点位，并开展不同结构型式沥青路面力学响应的研究.从疲劳寿命的角度，分析沥青层和基层的水平应力、应变指标的分布规律；从沥青层永久变形量的角度，分析竖向应力、应变及剪应力、剪应变指标的分布规律.通过分析沥青路面三向应力、应变及剪应力、剪应变在空间中的分布规律，给出建议计算图示，可大大提高今后新建路面结构验算的工作效率,也可为沥青路面结构内部应力应变响应规律的研究提供参考和依据.

1 计算模型及参数

为简化计算，将沥青路面视为线弹性层状体系，假定层间完全连续.文献[1]采用双轮组单轴载100 kN作为标准轴载，当量圆半径R=10.65 cm，轮胎接地压强p=0.7 MPa.

考虑到关键点位的位置可能随路面结构形式的不同而变化，因此，本文选择两种不同无机结合料稳定类基层沥青路面结构形式进行对比分析.其中，基层和底基层均为无机结合料稳定类，结构一各层模量均相同，结构二各层模量差异较大，为了排除泊松比的影响，各层泊松比均取为0.35.计算参数见表1.

设定YY方向为横断面方向，XX方向为行车方向，ZZ为深度方向，见图1.下文将相应方向上的力学响应分别简称为横向应力(变)、纵向应力(变)、竖向应力(变).

本文理论计算的前提是假定模型为线弹性体，因此，力学计算结果满足叠加原理，根据弹性力学相关知识，以分析最不利状态为原则，显然，通过双圆荷载圆心YZ断面(简称横断面)为最不利受力断面.因此，本文仅分析横断面上各点力学响应.在横断面上，沿横向间隔0.026 6 cm共选取15个点位，沿深度方向间隔1～4 cm不等共选取30个点位，15个点位Y坐标见表2.

表1 计算参数

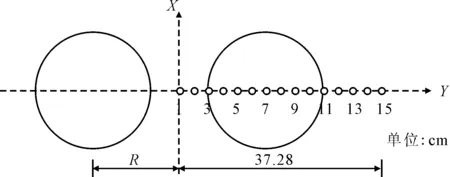
图1 横断面上沿YY方向(横向)计算点位选取

2 结构一力学响应结果

2.1 水平应力分析

水平应力包括纵向应力和横向应力，15个点位沿深度方向的水平应力分布见图2.①同一深度(除路表外)，各点位水平应力仅大小有差异，方向无变化，同为拉(压)应力；②参考现行规范，提取关键层层底的水平应力，见表3.沥青层底为压应力，最大值出现在点位1，表现为横向应力；基层底、底基层底均为拉应力，最大值出现在点位1，表现为纵向应力.

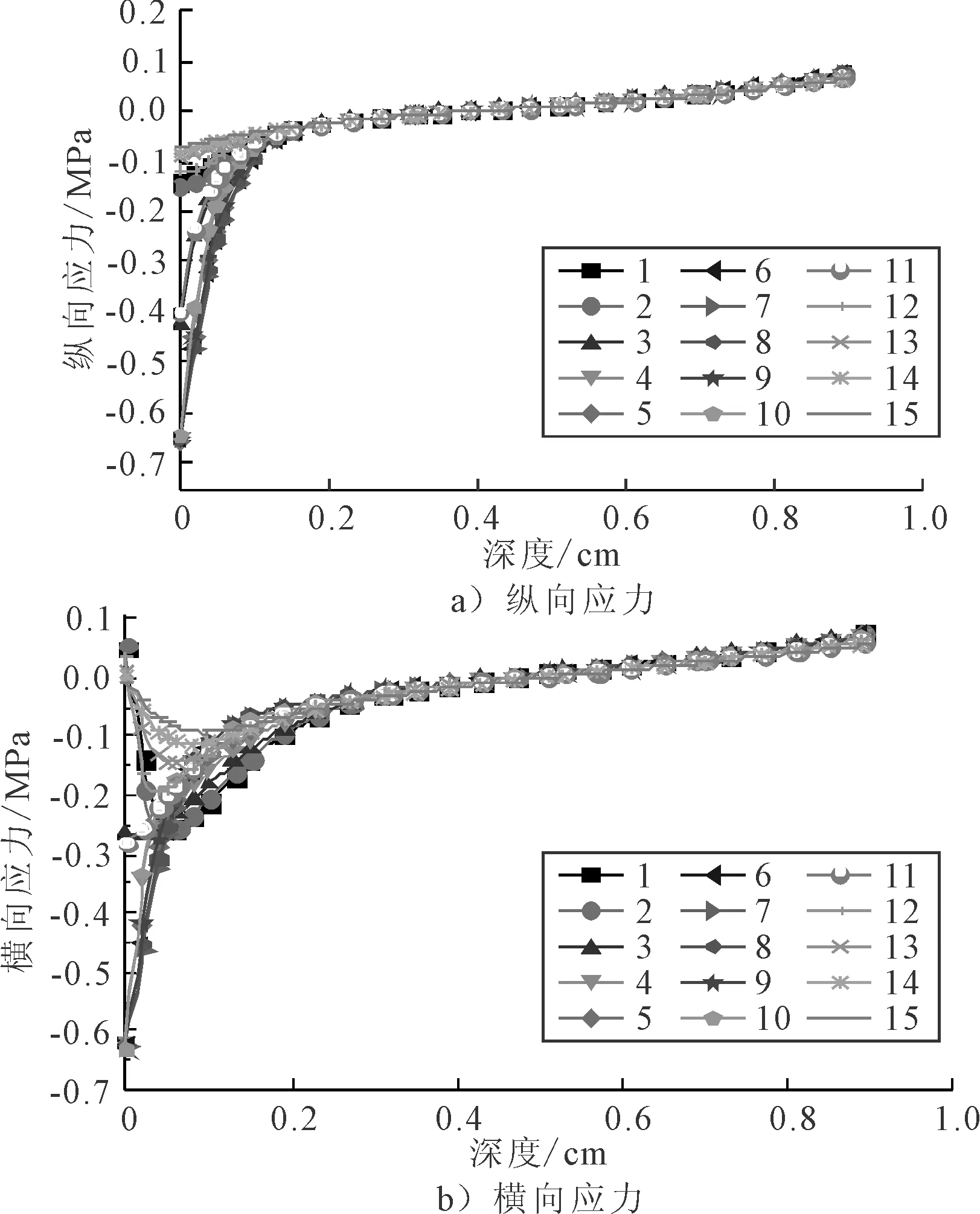
图2 水平应力沿深度分布图

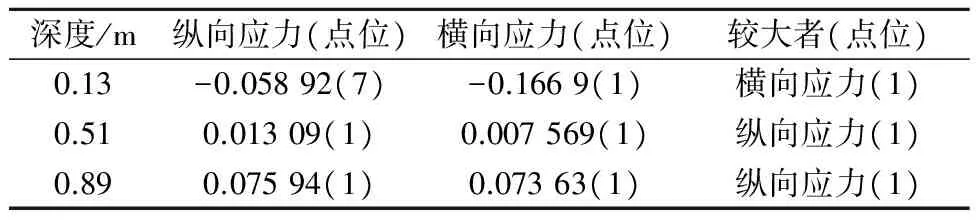
表3 结构一关键层底最大应力绝对值及点位 MPa

2.2 水平应变分析

水平应变包括纵向应变和横向应变，15个点位沿深度方向的水平应变分布见图3.根据沥青路面材料耐压不耐拉的特点，应变侧重研究拉应变分布规律.

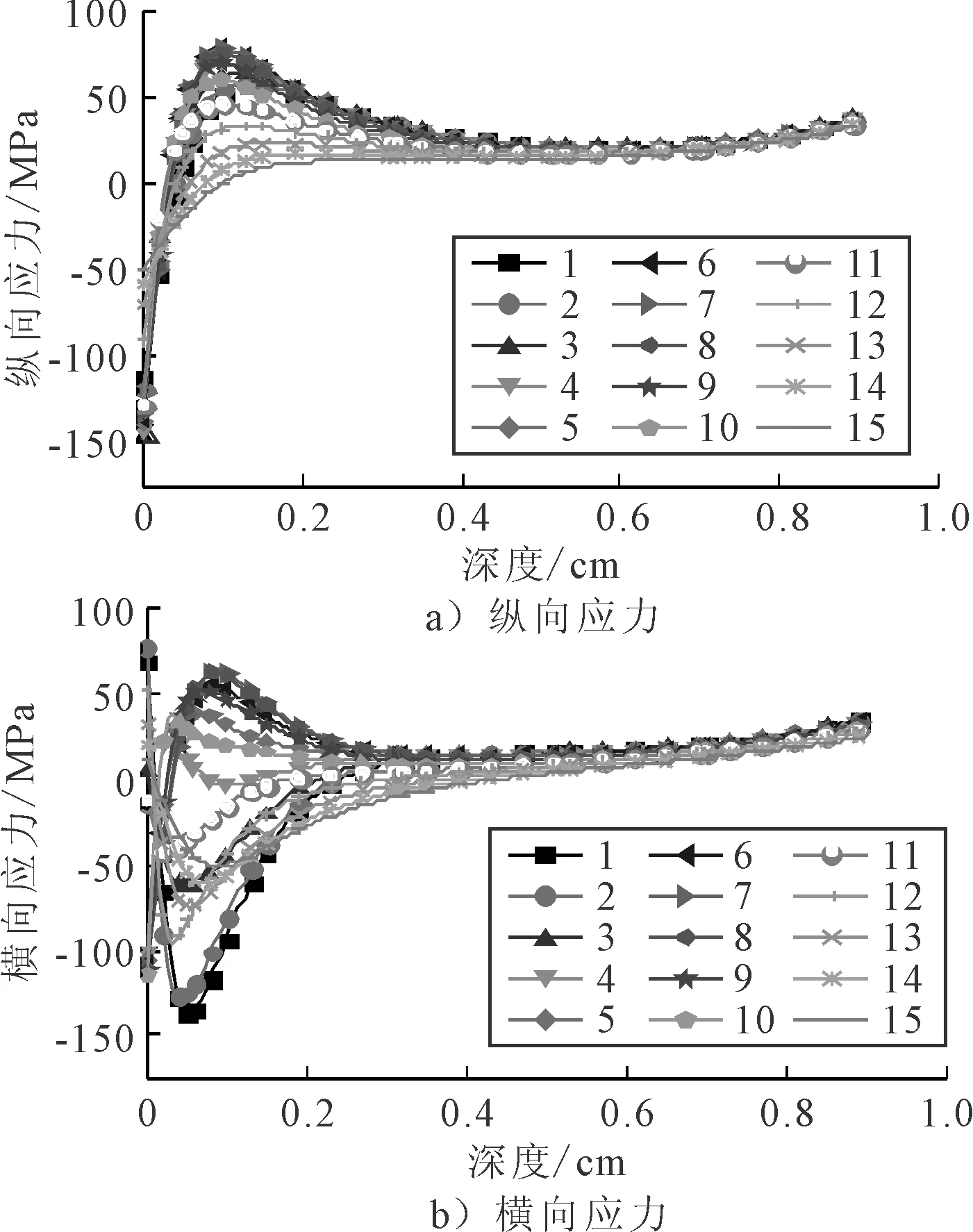
图3 结构一15个点位水平应变随深度分布图

由图3可知，①同一深度，各点位水平应变不仅大小有差异，且方向亦变化，邻近点位呈现拉压交替现象；②参考现行规范，各关键层底纵向应变显然大于横向应变，沥青层内拉应变普遍大于基层内拉应变，见表4.沥青层底、基层底、底基层底均为拉应变，最大值分别在点位6、点位1及点位1；③横向应变拉压交替出现次数大于纵向应变；④沥青层内最大纵向拉应变出现在点位7，数值78.07×10-6，深度0.1 m，并非在沥青层底.

表4 结构一关键层底最大应变绝对值及点位 ×10-6

2.3 竖向应力应变分析

15个点位沿深度方向的竖向应力应变分布见图4.竖向应力在轮胎接地面积范围内的点位4～10 均为轮强胎接地压强0.7 MPa，竖向应变在沥青面层内0～6 cm范围内沿横向分布依次为拉应变、压应变、拉应变，拉压交替，最大竖向压应变331.6×10-6距离路表6 cm，位于点位7.

图4 结构一15个点位竖向应力、应变随深度分布图

2.4 剪应力、剪应变分析

15个点位沿深度方向的剪应力、应变分布见图5.

图5 结构一15个点位剪应力、剪应变随深度分布图

由图5可知：①剪应力、剪应变变化规律完全一致，变化规律符合微元体在三向受力状态下剪切虎克定律τ=Gγ，剪应力与剪应变分析等效；②最大剪应力、剪应变出现点位相同，均出现在上面层，为点位10，深度为0.04 m，数值大小分别为0.217 MPa，209×10-6.

3 结构二力学响应结果

3.1 水平应力分析

水平应力包括纵向应力和横向应力，15个点位沿深度方向的水平应力分布见图6.

图6 结构二水平应力沿深度分布图

由图6可知，较结构一而言，结构二因基层模量增幅较大，加之下面层模量亦提高，其水平应力整体呈下降趋势，曲线走势不如结构一光滑，模量突变处，曲线存在尖点.但整体表现的规律与结构一基本相同：①同一深度(除路表外)，各点位水平应力方向无变化，同为拉(压)应力；②沥青层底最大压应力为点位6的横向应力，点位与结构一不同，应力方向相同，基层、底基层最大拉应力与结构一相同，见表5.

表5 结构二关键层底最大应力绝对值及点位 MPa

3.2 水平应变分析

水平应变包括纵向应变和横向应变，15个点位沿深度方向的水平应变分布见图7.结构二亦侧重研究拉应变分布规律.

图7 结构二15个点位水平应变随深度分布图

由图7可知，较结构一而言，因结构二模量整体的提高，结构二水平应变的整体水平低于结构一，层之间模量突变处，应变曲线存在尖点.但整体表现的规律与结构一基本相同：①同一深度，各点位水平应变大小、方向均变化，存在拉压交替现象；②沥青层底、基层底、底基层底均为拉应变，最大值分别出现在点位7、点位1及点位1，沥青层底拉应变与结构一点位不同，见表6；③横向应变拉压交替出现次数亦大于纵向应变；④沥青层内最大纵向拉应变出现在点位7，数值22.82×10-6，深度0.08 m，并非出现在沥青层底.

表6 结构二关键层底最大应变绝对值及点位 ×10-6

3.3 竖向应力、应变分析

15个点位沿深度方向的竖向应力、应变分布见图8.

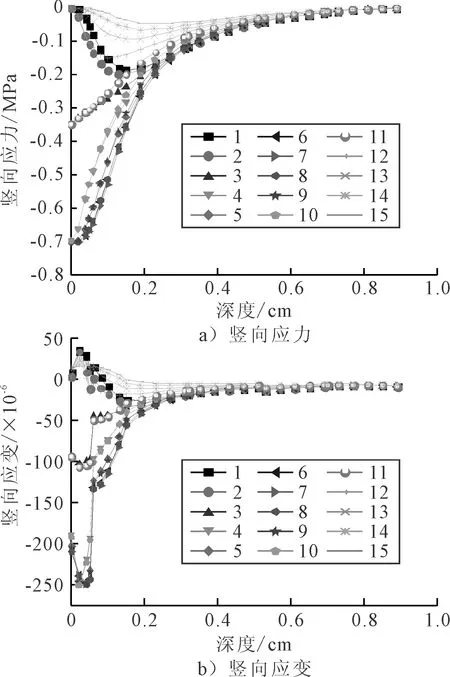
图8 结构二15个点位竖向应力、应变随深度分布图

由图8可知，竖向应力分布规律与结构一基本相同，在轮胎接地面积范围内的点位4～10 均为轮强胎接地压强0.7 MPa；随着基层模量的提高，竖向拉应变的影响深度扩大，达到8 cm；最大竖向压应变为250.7×10-6，距离路表2 cm，位于点位10，较结构一数值减小，位置上移；沿横向分布拉压交替仍存在.

3.4 剪应力、应变分析

15个点位沿深度方向的剪应力、应变分布见图9.较结构一而言，由于各层模量的变化，剪应力、剪应变变化规律并非完全一致，但最大剪应力、剪应变出现点位相同，均出现在上面层，为点位10，深度为0.04 m，数值大小分别为0.205 MPa，154×10-6.

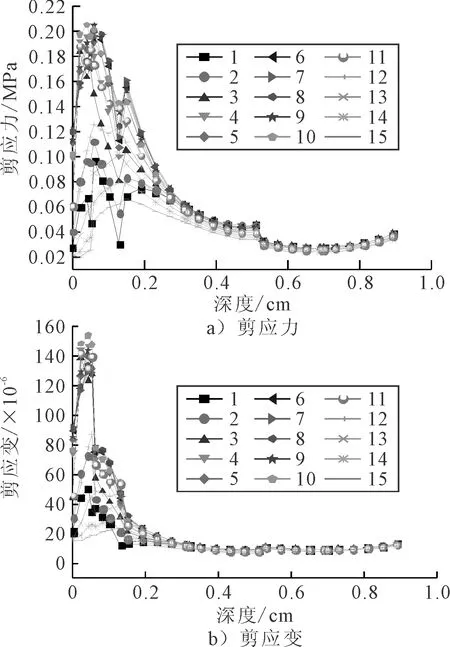
图9 结构二15个点位剪应力、应变随深度分布图

4 对比分析结果

4.1 点位对比分析

从计算无机结合料稳定类基层沥青路面疲劳寿命的角度，综合对比分析两种结构关键层位水平应力应变的关键点位，见表7.

表7 两种结构最大应力、应变方向及点位位置

由表7可知，两种不同结构沥青路面关键层位最大应力、应变方向一致，沥青层底均为横向应力和纵向应变，基层及底基层底均为纵向应力和纵向应变且点位相同.不同的是，沥青层底最大应力、应变出现的点位不同，且点位位置不能被现行规范提供的点位完全覆盖.

从计算无机结合料稳定类基层沥青路面沥青层永久变形量的角度，根据上文分析的结果，在轮胎接地范围内最大竖向压应力均为轮胎接地压强0.7 MPa，因此不再予以考虑.综合对比分析两种结构沥青层最大竖向压应变及最大剪应力、剪应变的关键点位，见表8.最大剪应力、剪应变点位均为10，深度均为0.04 m；而最大竖向压应变的点位和深度不同.

表8 两种结构最大剪应力、剪应变方向及点位位置

4.2 建议计算图示

由于本文只进行了两种不同结构类型的计算，考虑到实际路面结构形式多样，不能一概而论的给出最终点位，但可以确定的是，在轮胎接地面积内，应加密计算点位，点位横向间隔建议为0.026 6 m.针对计算无机结合料稳定类基层沥青路面疲劳寿命指标，加密模式建议为关键层层底点位1～7(共7点)，见表9；针对计算无机结合料稳定类基层沥青路面永久变形量指标，加密模式建议为沥青层点位7～10(共4点)，根据结构层厚度建议竖向取点间隔为0.01～0.02 cm，见表10.由表9～10可获取点位及点位处待提取力学指标的类型和方向.

表9 验算疲劳寿命建议计算图示

表10 验算沥青层永久变形量建议计算图示

5 结 束 语

针对现行规范提供的计算点位少、点位间距大、应力应变方向不确定的问题，本文通过加密计算点位，通过开展不同结构型式沥青路面力学响应研究，对比分析了不同结构类型沥青路面三向应力、应变及剪应力、剪应变空间分布规律.在此基础上，从验算疲劳寿命和沥青层永久变形量两个角度，分别给出了建议的计算图示.可根据工程项目需要查表选择点位及点位处需计算的力学指标，再得到力学指标的结果后，比较选择最大值便可进行疲劳寿命和沥青层永久变形量的验算工作.建议的计算图示可提高今后新建路面结构验算的工作效率,也可为沥青路面结构内部应力应变响应规律的研究提供参考和依据.

[1] 中华人民共和国交通部.公路沥青路面设计规范: JTG D50—2006[S].北京：人民交通出版社,2006.

[2] 刘锋,李浩,方杨.双层刚性道路结构参数反演分析[J].武汉理工大学学报(交通科学与工程版),2016,40(6)：994-997.

[3] 杨永顺,王林,韦金城.马士杰重载作用下典型路面结构动态响应数据采集与分析[J].公路交通科技, 2010,27(5)：11-16.

[4] 董泽蛟,曹丽萍,谭忆秋,等.移动荷载作用下沥青路面三向应变动力响应模拟分析[J].土木工程学报,2009,42(4)：133-139.

[5] 王甲辰,李浩,吴传海,等.湿热重载地区长寿命沥青路面动态响应实测系统研究[J].中外公路,2016,36(2)：58-62.

[6] 阮文,胡圣魁,陈泽宏,等.基于膨胀机理的钢渣基层材料体积安定性研究[J].公路,2013(4):169-174.

[7] 李飞,陈勇鸿,高伏良,等.掺钢渣无机结合料稳定路面基层材料干缩温缩试验研究[J].公路,2012(12):186-191.

[8] 雷谱春.半刚性材料抗裂性能试验研究[J].筑路机械与施工机械化,2016(12):72-74.

[9] 王浩.二次曲线拟合法在无机结合料稳定材料击实试验中的应用研究[J].城市建设理论研究(电子版),2015(8):3024-3025.

[10] 李小刚.无机结合料稳定类基层疲劳损坏预估模型研究[D].西安：长安大学,2006.